Вспоминаем
В прошлой части мы искали коллизии самым примитивным образом - перебирали все пары объектов и сравнивали сумму их радиусов с расстоянием между их центрами. При таком подходе максимальное число объектов, которое наш движок мог выдержать, составляло несколько сотен.
Возникает закономерный вопрос: зачем проверять на пересечение окружности, которые находятся далеко друг от друга?
Действительно, теперь мы будем поступать чуть хитрее.
Сетка
Идея состоит в том, чтобы разбить наш экран на такую сетку, в каждую ячейку которой мы сможем вписать окружность — тогда с каждой окружностью теоретически могут иметь пересечения только окружности, чьи центры находятся в соседних (включая нашу) клетках. Если размер ячеек будет больше или меньше, то такое рассуждение будет неверным (можно легко представить контр‑примеры).
Эта самая сетка будет представлять из себя массив, в каждой ячейке которого мы будем хранить ссылки на объекты, центры которых находятся в этой ячейке. Будем итерироваться по всем ячейкам, кроме крайних (для удобства). И для каждой окружности в текущей ячейке искать 'кандидатов' на коллизию в соседних.
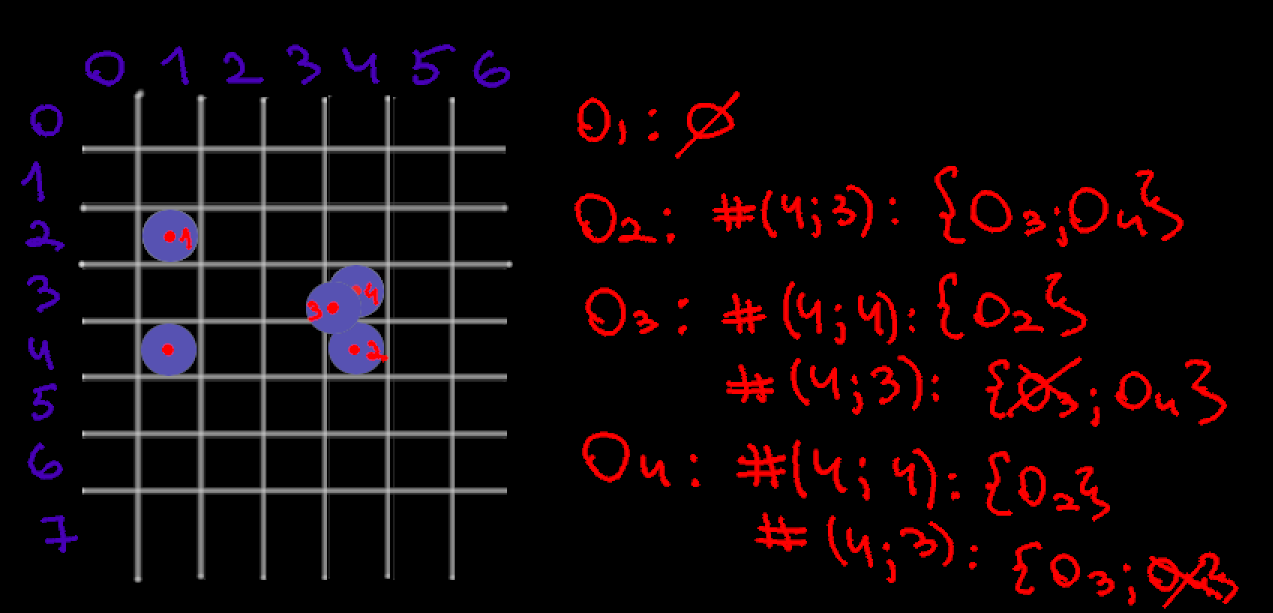
Дальше нам останется проверить наличие коллизий между нашей окружностью и всеми 'кандидатами' и при наличии таковых — разрешить их как в прошлый раз.
Напишем класс для сетки, основываясь на всем этом:
Grid.hpp
// constants::gridStep = 2 * radiusOfObject
// Класс ячейки чисто ради удобства
struct Cell {
std::vector<VerletObject *> cellObjects;
Cell() : cellObjects{} {}
};
struct CollisionGrid {
// Сетка будет больше экрана на определенную величину с каждой стороны
// Чтобы объект, например, подлетевший высоко наверх
// за экран, мог вернуться назад
const int width =
(constants::screenWidth + 2 * constants::worldBorderFromScreen) /
constants::gridStep;
const int height =
(constants::screenWidth + 2 * constants::worldBorderFromScreen) /
constants::gridStep;
std::vector<std::vector<Cell>> grid;
CollisionGrid() : grid(height, std::vector<Cell>(width)) {}
// Я решил втупую заново заполнять сетку после каждой
// итерации цикла движка - самый простой способ
void updateGrid(std::vector<VerletObject *> &objects) {
for (int x = 0; x < width; ++x) {
for (int y = 0; y < height; ++y) {
grid[y][x].cellObjects.clear();
}
}
auto object = std::begin(objects);
while (object++ != std::end(objects)) {
if (*object == nullptr || object == std::end(objects))
return;
// Не забываем прибавить worldBorderFromScreen, чтобы
// перейти в систему отсчета экрана
int objx =
(*object)->positionCurrent.x + constants::worldBorderFromScreen;
int objy =
(*object)->positionCurrent.y + constants::worldBorderFromScreen;
// Если объект за границами 'мира' - удаляем его
if (objx / constants::gridStep >= width ||
objy / constants::gridStep >= height || objx < 0 || objy < 0) {
objects.erase(object);
continue;
}
grid[objy / constants::gridStep][objx / constants::gridStep]
.cellObjects.push_back(*object);
}
}
// Для читаемости кода в основном методе
bool isCollideable(VerletObject *object1, VerletObject *object2) {
if (object1 == object2 || !object1->isMoveable)
return false;
return true;
}
// Разрешении коллизии осталось аналогичным
void collide(VerletObject *object1, VerletObject *object2) {
Vec2<float> collisionAxis =
object1->positionCurrent - object2->positionCurrent;
const float dist = collisionAxis.length();
if (dist > object1->radius + object2->radius)
return;
Vec2<float> normalized = collisionAxis / dist;
const float delta = object1->radius + object2->radius - dist;
object1->positionCurrent += normalized * delta * 0.5f;
object2->positionCurrent -= normalized * delta * 0.5f;
}
// Сюда мы будем передавать координаты ячейки, на которую смотрим
void collidecell(int x, int y) {
// Для каждого ее объекта
for (auto object1 : grid[y][x].cellObjects) {
// В каждой из соседних ячеек
for (int dx = -1; dx < 2; ++dx) {
for (int dy = -1; dy < 2; ++dy) {
// Для каждого из объектов, лежащих в них
for (auto object2 : grid[y + dy][x + dx].cellObjects) {
// Проверяем коллизию
if (!isCollideable(object1, object2))
continue;
collide(object1, object2);
}
}
}
}
}
};Осталось лишь добавить эту сетку в класс движка и написать метод для ее обхода:
Тут немного
private:
CollisionGrid grid;
//...
//...
void solveCollisions(){
for(int x = 1; x < grid.width - 1; ++x) {
for(int y = 1; y < grid.height - 1; ++y) {
grid.collidecell(x, y);
}
}
}
//...
//...
void update(float dt) {
//...
solveCollisions();
grid.updateGrid(objects);
//...
}Отлично! Самое время перейти от примивных тел к чему‑то более сложному.
Link.hpp
Теперь напишим линки — жесткие связи между объектами. Так мы получим возможность создавать различные структуры.
Задача нашего линка состоит в том, чтобы сохранять постоянное расстояние между объектами, которые он соединяет. т. е. если расстояние между ними отличается от длины линка, то мы должны подвинуть их вдоль него на разницу расстояния между объектами и длины линка.

Так и запишем
struct Link {
// Будем хранить ссылки на объекты, которые линк связывает
eng::VerletObject *object_1;
eng::VerletObject *object_2;
// Длина линка
float targetDist;
// Для его отображения
sf::Vertex line[2];
// Конструктор
Link(eng::VerletObject *obj_1, eng::VerletObject *obj_2, float targDist)
: object_1{obj_1}, object_2{obj_2}, targetDist{targDist} {}
// Применяем рассуждение с картинки
void apply() {
const eng::Vec2<float> axis =
object_1->positionCurrent - object_2->positionCurrent;
const float dist = axis.length();
const eng::Vec2<float> normalized = axis / dist;
const float delta = targetDist - dist;
object_1->positionCurrent += normalized * delta * 0.5f;
object_2->positionCurrent -= normalized * delta * 0.5f;
line[0] = sf::Vertex(
sf::Vector2f(object_1->positionCurrent.x, object_1->positionCurrent.y),
sf::Color::White);
line[1] = sf::Vertex(
sf::Vector2f(object_2->positionCurrent.x, object_2->positionCurrent.y),
sf::Color::White);
}
};Закономерно добавляем в класс движка публичный метод для добавления линка и приватный метод для вызова apply() от всех линков, который будем вызывать каждый кадр (в update()).
Тут все просто
//...
void applyLinks() {
if (!links.size())
return;
for (auto *link : links) {
link->apply();
}
}
void drawLinks() {
if (!links.size())
return;
for(auto *link: links) {
window->draw(link->line, 2, sf::Lines);
}
}
//...//...
void update(float dt) {
//...
applyLinks();
//...
}//...
void addLink(eng::VerletObject *obj_1, eng::VerletObject *obj_2,
float targDist) {
Link *link = new Link(obj_1, obj_2, targDist);
links.push_back(link);
}
//...Со штуками, которые мы теперь можем создавать можно было поэксперементировать (очень рекомендую), но я решил пока что остановится на простых квадратах.
Можно сделать и за один проход, но так нагляднее
void addSquare(float pos_x, float pos_y, float size, sf::Color color) {
int objectsInRow = size / constants::objRadius / 2 + 1;
float linklength = constants::objRadius * 2.f;
std::vector<std::vector<VerletObject *>> square(
objectsInRow, std::vector<VerletObject *>(objectsInRow));
for (float y = pos_y, i = 0; y <= pos_y + size;
y += constants::objRadius * 2, ++i) {
for (float x = pos_x, j = 0; x <= pos_x + size;
x += constants::objRadius * 2, ++j) {
addObject(x, y, constants::objRadius, false, color);
square[i][j] = objects[objects.size() - 1];
}
}
for (int y = 0; y < objectsInRow; ++y) {
for (int x = 0; x < objectsInRow; ++x) {
if (x < objectsInRow - 1)
addLink(square[y][x], square[y][x + 1], linklength);
if (y >= 1)
addLink(square[y][x], square[y - 1][x], linklength);
if (y >= 1 && x >= 1)
addLink(square[y][x], square[y - 1][x - 1], linklength * sqrt(2));
}
}
}Посмотрим, что получается:
Выглядит так себе. К счастью, такую проблему можно легко решить: мы просчитываем положения объектов (update) один раз за кадр, давайте повысим точность вычислений — будем делать это несколько раз.
Update'им метод update
//...
void update(float dt) {
int iterations = constants::physicSteps; // у меня - 8
dt = dt / static_cast<float>(iterations);
while (iterations--) {
applyGravity();
applyLinks();
applyConstraint();
solveCollisions();
updatePositions(dt);
}
drawObjects();
drawLinks();
}
//...
Что теперь? Теперь наша симуляция может выглядить (по сравнению с тем, что было в первой части) достаточно интересно.
Кстати, почему мы все делаем на одном потоке, когда ничего (практически) не мешает нам распараллелить обход сетки? Это даст достаточно ощутимый прирост производительности.
Спойлер: симуляция на 8 потоках
Однако из‑за многопоточности могут возникать различные спецэффекты. Если наберется достаточно материала, то обязательно напишу об этом отдельную статью.
Всем спасибо, кто дочитал!