Синтез фракталов: IFS и L-системы

Введение

[1]
Фракталом (лат.«fractus» – дроблёный, сломанный, разбитый) называют сложную геометрическую фигуру, обладающую свойством самоподобия, т.е. составленной из нескольких частей, каждая из которых подобна целой фигуре. В более широком смысле под фракталами понимают множества точек в евклидовом пространстве, имеющие промежуточную (дробную) метрическую размерность (размерность Хаусдорфа).
Размерность Хаусдорфа – естественный способ определить размерность множества в метрическом пространстве. Размерность Хаусдорфа согласуется с нашими обычными представлениями о размерности в тех случаях, когда эти обычные представления есть. Например, в трёхмерном евклидовом пространстве хаусдорфова размерность конечного множества равна нулю, размерность гладкой кривой – единице, размерность гладкой поверхности – двум и размерность множества ненулевого объёма – трём.

Фракталы бывают нескольких типов:

• Геометрические фракталы – самый наглядный класс фракталов. В двухмерном простран-стве их получают с помощью некоторой ломаной (или поверхности в трехмерном простран-стве), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ло-маную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате беско-нечного повторения этой процедуры, получается геометрический фрактал.
• Алгебраические фракталы – это самая крупная группа фракталов. Получают их с помо-щью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процес-сы. Интерпретируя нелинейный итерационный процесс как дискретную динамическую систему, можно пользоваться терминологией теории этих систем: фазовый портрет, установившийся процесс, аттрактор и т.д. Известно, что нелинейные динамические системы обладают несколькими устойчивыми состояниями. То состояние, в котором оказалась динамическая система после некоторого числа итераций, зависит от ее начального состояния. Поэтому каждое устойчивое состояние (или как говорят — аттрактор) обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемые конечные состояния. Таким образом, фазовое пространство системы разбивается на области притяжения аттракторов. Если фазовым является двухмерное пространство, то, окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы (итерационного процесса). Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами. Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные нетривиальные структуры.
• Стохастические фракталы являются ещё одним известным классом фракталов, которые получаются в том случае, если в итерационном процессе случайным образом менять какие-либо его параметры. При этом получаются объекты очень похожие на природные — несимметричные деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.

Кроме этих существуют так же:

• Рукотворные фракталы
• Природные фракталы
• Детерминированные фракталы
• Недетерминированные фракталы

В рамках данной статьи будут рассмотрены способы генерации этих фракталов: L-системы и системы итерированных функций.

1. Системы итерированных функций

Традиционно в математике, пространства и множества содержат в себе точки. Однако же, суще-ствуют пространства, в которых “точки” сами являются множествами. С математической точки зрения, достоинство абстрагирования от точки состоит в достижении общности.
Пример этого – сжимающие отображения и связанные с ними теоремы сходимости. Сжимаю-щие отображения определяются в метрических пространствах как отображения уменьшающие расстояния между точками. Сжимающие отображения обладают важным свойством. Если взять любую точку и начать итеративно применять к ней одно и то же сжимающее отображение: f(f(f...f(x))), то результатом будет всегда одна и та же точка. Чем больше раз применим, тем точ-нее найдем эту точку. Называется она неподвижной точкой и для каждого сжимающего отоб-ражения она существует, причем только одна. Системы итерированных функций (IFS) являются примером применения этой теории.

1.1 Определение

Система итерированных функций это конечный набор функций Fi: X -> X в метрическом про-странстве X. Каждая из них расширяется до отображения Fi: H(X) -> H(X), где H(X) это пространство точки которого являются непустыми сжатыми подмножествами X. Если использовать Хаусдорфову метрику, то H(X) полно если X было полным. Кроме того, сжатия FiX X остаются сжатиями и на H(X). В совокупности, {Fi} определяют новое сжатие F: H(X) -> H(X), по следующей формуле: для каждого A∈H(X), F(A) = ∪Fi(A). Из общей теории, для полного метрического пространства X, F имеет фиксированную точку AF: F(AF) = AF, которую можно достичь последовательными приближениями из любой начальной точки. Фиксированные точки IFS иногда называются аттракторами или инвариантами.

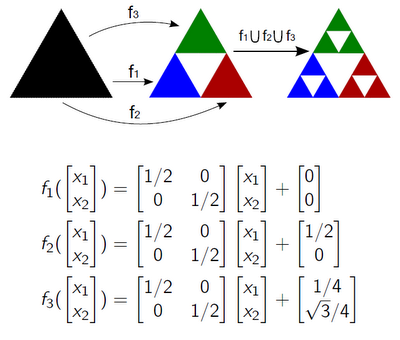
Рисунок 6. Пример построения треугольника Серпинского с помощью IFS.
Таким образом, возникают две задачи. Первая – это нахождение аттрактора заданной IFS. Вто-рая проблема противоположна первой: для заданного множества A∈H(X), найти IFS {Fi} для которой A является аттрактором.

1.2 Детерминированный алгоритм

Первая проблема решается с помощью детерминированного алгоритма.
Начнем с множества A0∈H(X) и станем последовательно вычислять
Ak = ∪Fi(Ak-1) = F(Ak-1), k > 1. Ряд {Ak) сходится к аттрактору AF при k.

1.3 Алгоритм случайных итераций

Математика альтернативного алгоритма – алгоритма случайных итераций, сложнее, но его при-менение проще. Сопоставим позитивные частоты pi отображениям Fi. Начнем с произвольной точки x0∈X. На каждом шаге k+1, выберем xk+1 из множества {Fi(xk)}. Fj(xk) выбирается с веро-ятностью pj / pi. Последовательность[5] {xk} сходится к AF. На практике, чтобы изобразить при-ближение AF на компьютере, точки последовательности выводятся на экран. Числа {pi} никак не изменяют AF, но существенно влияют на процесс отображения его приближений.

1.4 Теорема коллажа

Обратная задача приближенно решается теоремой коллажа. Цитируя М. Барнсли: “теорема го-ворит нам, что чтобы найти IFS аттрактор которой “похож” на данное множество необходимо найти набор сжимающих отображений некоторого большего множества включающего своим подмножеством исходное множество, таких, что объединение, или коллаж, отображений этого множества аппроксимировало бы исходное множество”.

1.5 Использование

[2]
Основной областью применения IFS является сжатие изображений. Произвольные изображения, в отличие от фракталов, не самоподобны, так что так просто эта задача не решается. Как это сделать придумал в 1992 году Арнольд Жакин, в то время — аспирант Майкла Барнсли.
Самоподобие необходимо — иначе ограниченные в своих возможностях аффинные преобразо-вания не смогут правдоподобно приблизить изображения. А если его нет между частью и целым, то можно поискать между частью и частью.
Упрощенная схема кодирования выглядит так:

• Изображение делится на небольшие неперекрывающиеся квадратные области, называе-мые ранговыми блоками.
• Строится пул всех возможных перекрывающихся блоков в четыре раза больших ранго-вых — доменных блоков.
• Для каждого рангового блока по очереди «примеряем» доменные блоки и ищем такое преобразование, которое делает доменный блок наиболее похожим на текущий ранго-вый.
• Пара «преобразование — доменный блок», которая приблизилась к идеалу, ставится в соответствие ранговому блоку. В закодированное изображение сохраняются коэффициенты преобразования и координаты доменного блока. Содержимое доменного блока нам ни к чему — вы же помните, нам все равно с какой точки стартовать.

На картинке ранговый блок обозначен жёлтым, соответствующий ему доменный — красным. Также показаны этапы преобразования и результат.

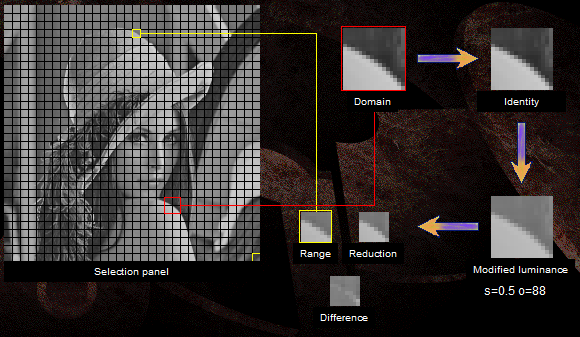
Рисунок 7. Пример сжатия изображения.
Получение оптимального преобразования — отдельная тема, однако большого труда оно не составляет. Но другой недостаток схемы виден невооруженным глазом. Двухмегапиксельное изображение будет содержать огромное число доменных блоков размером 32x32. Полный их перебор для каждого рангового блока и есть основная проблема такого вида сжатия — коди-рование занимает очень много времени. С этим борются при помощи различных ухищрений, вроде сужения области поиска или предварительной классификации доменных блоков.

Декодирование же производится просто и довольно быстро. Берем любое изображение, делим на ранговые области, последовательно заменяем их результатом применения соответствующего преобразования к соответствующей доменной области (что бы она ни содержала в данный мо-мент). После нескольких итераций исходное изображение станет похоже на себя:

Рисунок 8. Пример восстановления сжатого изображения.

2. Системы Линденмайера

[3]
Красота растений привлекала внимание математиков веками. Активнее всего изучались инте-ресные геометрические свойства растений, такие как симметрия листьев относительно центральной оси, радиальная симметрия цветов, и спиральное расположение семечек в шишках. «Красота связана с симметрией» (H. Weyl. Symmetry). Во время роста живых организмов, особенно растений, можно четко видеть регулярно повторяющиеся многоклеточные структуры. В случае составных листьев, например, маленькие листочки, которые являются частью большого взрослого листа, имеют ту же форму, что весь лист имел на раннем этапе формирования.

В 1968г. Венгерский биолог и ботаник Аристид Линденмайер (Aristid Lindenmayer) предложил математическую модель для изучения развития простых многоклеточных организмов, которая позже была расширена и используется для моделирования сложных ветвящихся структур — разнообразных деревьев и цветов. Эта модель получила название Lindenmayer System, или про-сто L-System.

2.1 Основные идеи

Основная идея L-систем — постоянная перезапись (rewriting) элементов строки. О чем это? В данном случае перезапись — это способ получения сложных объектов путем замены частей простого начального объекта по некоторым правилам. Классическим примером является сне-жинка Коха. На рисунке инициатор — это начальный объект, грани которого заменяются на объект-генератор. Далее с новым объектом проделывается то же самое.

Рисунок 1. Снежинка Коха.

Возвращаясь к L-системам и проводя аналогию с фракталами, можно сказать, что L-система оперирует со строкой символов по специальным правилам, начиная с первоначальной простой аксиомы. Таким образом, L-система является математической грамматикой. Но фундаменталь-ное отличие L-систем от формальных грамматик состоит в том, что правила применяются одно-временно ко всей строке, к каждому символу, плюс, нет понятий терминальных и нетерминаль-ных символов. То есть «вывод» по этой грамматике может продолжаться бесконечно.
На следующей картинке видно соотношение между контекстно-свободными (OL), контекстно-зависимыми (IL) L-системами и другими формальными грамматиками в иерархии Хомского.

Рисунок 2. Иерархия Хомского.

2.2 Простейшие L-системы

Также, как и в классификации Хомского, L-системы имеют и свою классификацию от простых до сложных и мощных.
Самым простым примером являются детерминированные контекстно-свободные L-системы или сокращенно DOL. Я не люблю формальные определения грамматик, так что скажу просто своими словами. Есть некоторый набор символов — алфавит. Этим алфавитом записывается строка, с которой работает L-система. Есть аксиома — первоначальная строка из одной или более буквы и набор правил вида a → ab. Во время каждой итерации алгоритма, применяя правило к букве из текущей строки, она (буква) заменяется на набор букв справа от стрелки. Проще рассмотреть конкретный пример развития многоклеточного организма Anabaena catenula, который изучал Линденмайер, когда он предложил модель L-систем.
Пусть наш алфавит состоит из следующих символов, каждый из которых обозначает некоторую клетку: alar bl br.
Аксиома состоит из одного символа:
ω: ar
И четырех правил.
p1: ar → albr
p2: al → blar
p3: br → ar
p4: bl → al

Правила говорят, какие символы меняются на какие в процессе роста организма. На картинке видно как, применяя правила мы наблюдаем «деление» клеток и развитие.

Рисунок 3. L-система симулирующая развитие Anabaena catenula.

2.4 Использование LOGO

Пока мы видели как нарисовать одномерную бактерию, но с помощью известного детского языка программирования LOGO, в котором предлагается управлять черепашкой и рисовать фи-гуры на экране, можно будет уже рисовать двумерные и трехмерные фракталы и повторяющие-ся структуры. Как? Все просто. Берем алфавит, в котором каждый символ означает некоторую команду для двумерной или трехмерной черепашки:

• F — продвинуться вперед и нарисовать линию
• f — продвинуться вперед ничего не рисуя
• + — повернуть влево
• — — повернуть вправо
• & — повернуть вниз
• ^ — повернуть вверх
• \ — наклониться влево
• / — наклониться вправо
• | — развернуться на 180 градусов

Эти команды используют стандартные значения угла поворота δ, длины шага и базисные векторы двумерного и трехмерного пространства. Примеры двумерных фракталов и порожда-ющих их L-системы можно увидеть на следующей картинке:

Рисунок 4. Примеры L-систем.

2.5 Растения и ветвящиеся структуры

Все, что было до этого является, в общем-то, непрерывными кривыми. Такой способ моделиро-вания не подходит для моделирования растений с их ветвящейся топологией. Для этого в алфа-вит были добавлены символы [ и ], которые обозначают начало и конец ветвления соответ-ственно. Когда черепашка встречает символ [, ее текущее состояние пишется в стек и извлекает-ся оттуда при встрече символа ]. Уже такой простой грамматикой можно сгенерировать доволь-но интересные двумерные и трехмерные объекты похожие на деревья.

Рисунок 5. Примеры ветвящихся L-систем.

2.6 Стохастические L-системы

Стохастические L-системы добавляют возможность задания вероятности выполнения того или иного правила, и в общем случае не являются детерминированными, ибо разные правила могут иметь один и тот же символ слева. Это вносит некоторый элемент случайности в получающиеся структуры.

2.7 Контекстно-зависимые L-системы

Так же, как и контекстно зависимость в формальных грамматиках, в L-системы синтаксис пра-вил усложняется и принимает во внимание окружение заменяемого символа.

2.8 Параметрические L-системы

К каждому символу добавляется параметр-переменная (возможно не одна), которая позволяет, например, указывать величину угла поворота для + и -, длину шага и толщину линии, проверять условия для применения правила, считать количество итераций и передавать «сигналы» вперед и назад. Пример параметрической L-системы.

ω: B(2)A(4, 4)
p1: A(x, y) :y <= 3 → A(x ∗ 2, x + y)
p2: A(x, y) :y > 3 → B(x)A(x/y, 0)
p3: B(x) :x < 1 → C
p4: B(x) :x >= 1 → B(x − 1)

Параметрические контекстно-зависимые L-системы позволяют моделировать рост многокле-точных организмов и растений с учетом биохимических процессов и окружающей среды.

2.9 Использование

Еще в конце 80х L-системы использовались для визуализации моделей растений. Сейчас воз-можности компьютеров ушли далеко вперед. Многие игры и инструменты 3d моделирования используют процедурную генерацию контента, в том числе и L-системы. Как видите, из набора простых правил можно получить огромное количество разных растений и засадить ими целые поля.