И снова всем привет! В прошлый раз я раскрыл решение ZeroNightsCrackMe. Все кто успел его вовремя решить, мог получить приглашение на экскурсию в один из офисов Лаборатории Касперского, а так же подарок, в виде лицензионного ключа на три устройства. Но, помимо всего прочего, в Касперском сообщили, что крякми был облегченным, т.е. существует более сложная его версия и она будет разослана тем, кто пожелает её посмотреть (но без подарков, в своё удовольствие, так сказать). Конечно же я не мог отказать себе в том, чтобы не покрутить эту версию, поэтому подтвердил свое желание на участие.
17 февраля пришло письмо с новым крякми. Именно о его решении (и не только) я и поведаю в этой статье.
Параметры крякми те же:
Инструменты:
Приступим к решению…
Как обычно запускаем подопытного и проводим поверхностный анализ. Реакция аналогична прошлому крякми.
Рис. 1
Зная принцип работы прошлого крякми, приступим к поиску ключевых моментов и найдем:
После чего сравним все ключевые моменты с предыдущей версией и найдем отличия.
Первым делом найдем функцию обработки введенных данных. Делается это довольно просто. Жмем правой кнопкой мыши в окне дизассемблера и выбираем «Search for => All referenced strings»:
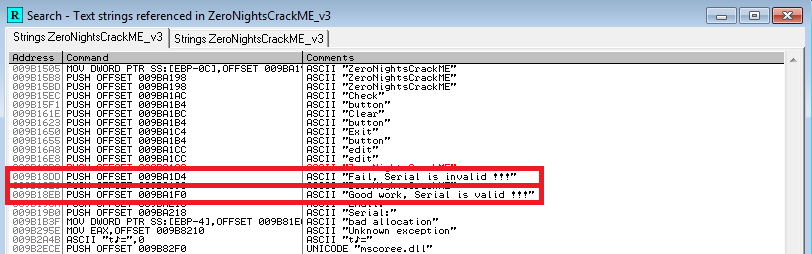
Рис. 2
Далее жмем по строке «Good work, Serial is valid !!!» и попадаем сюда:

Рис. 3
Выше и будет находиться искомая функция (в моем случае это CALL 0x9b12b0). Ей передается три параметра. В Arg2, Arg1 передается размер серийного кода и указатель на серийный код соответственно, а в регистре ECX указатель на email.
Заходим внутрь функции и крутим в самый низ, там находится алгоритм проверки таблицы валидации (идентичный старой версии):

Рис. 4
Ставим брейкпойнт в начале алгоритма и запускаем крякми на выполнение (разумеется, предварительно введя любые данные и нажав кнопку Check).

Рис. 5. Вводим тестовые данные
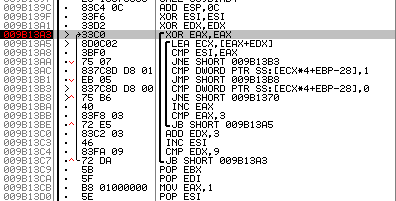
Рис. 6. Остановка на таблице валидации
Теперь определим адрес самой таблицы. Сделать это можно перейдя на строку «CMP DWORD PTR SS:[ECX*4+EBP-28],1» и подсмотрев целевой адрес.

Рис. 7. Определение адреса таблицы валидации
В моем случае адресом таблицы является 0x36f308 (выделено красным).

Рис. 8. Дамп таблицы валидации
Поиск алгоритма производим тем же способом, который был продемонстрирован при решении прошлого крякми, а именно:
Если все было сделано правильно, окажетесь здесь:
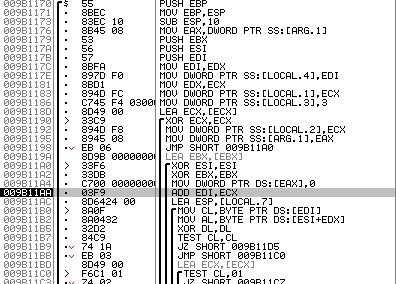
Рис. 9. Алгоритм заполнения таблицы валидации
Если сравните новый алгоритм со старым, то заметите, что они отличаются:
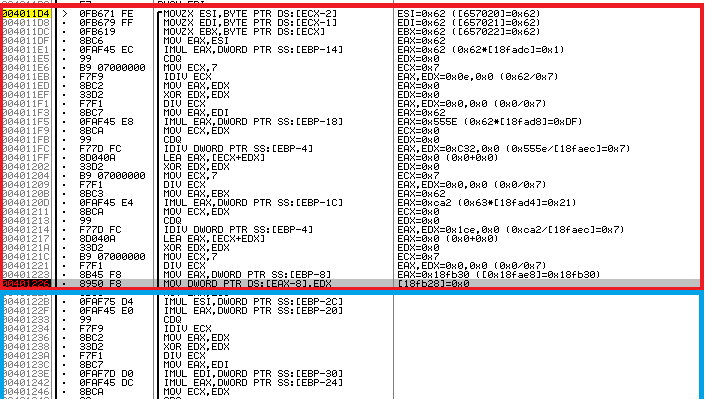
Рис. 10. Старый алгоритм (скриншот из прошлой статьи)
Представление «нового алгоритма» на Питоне выглядит следующим образом:
Перейдем к поиску данных которые используются этим алгоритмом.
Проанализировав код алгоритма было обнаружено два места, откуда берутся данные для его работы:

Рис. 11. Массивы с которыми оперирует новый алгоритм
Выше они выделены серым прямоугольником. В моем случае, по адресам 0x9b11b0 и 0x9b11b2, идет обращение к следующим массивам:

Рис. 12

Рис. 13
В каждом массиве находится 9 элементов по одному байту.
Если бы мы решали старый крякми, то мы бы сейчас перешли к поиску алгоритма превращения серийного кода во внутреннее представление, но в новом крякми было обнаружено существенное отличие от поведения старого крякми, поэтому ниже дана информация об отличиях, которые заключается вот в чём.
В старой версии крякми работа с серийным кодом происходила следующим образом:
В итоге у нас получалось что-то вроде этого:
В новой же версии всё немного усложнилось:
В итоге получаем что-то вроде этого:
Откуда следует, что у нас появляется зависимость от фиксированного массива.
Поиск конвертера серийного кода я оставлю за вами и здесь приводить не буду. Поиск можно осуществлять тем же способом, что и в старой версии.
Таблица и допустимый диапазон идентичны старой версии.
Теперь когда все необходимые элементы были собраны можно приступать к решению.
Алгоритм наших действий следующий:
Если вы читали первую статью, то наверное помните, что для составления требуемой таблицы [1, 0, 0, 0, 1, 0, 0, 0, 1], необходимо иметь такие байты, которые бы при взаимодействии друг с другом давали либо «нули», либо «единицы».
В старой версии крякми найти эти байты было очень просто. Всё что нужно было сделать это перебрать весь доступный алфавит и применить к нему несколько простых операций.
В новой версии это сделать намного сложнее (но это только на первый взгляд и ниже я объясню почему). В старой версии мы могли перебирать по одному элементу. В новой версии мы должны перебирать по три элемента, так как все они взаимно связаны.
Потому что в первой статье я не раскрыл ту «магию», которая в действительности была скрыта за поиском «нулей» и «единиц» (в этой статье её придется раскрыть, хотя можно было этого не делать). В своём кейгене я использовал функцию, которая ищет требуемые «нули» и «единицы», но не совсем очевидным способом. Это помогло успешно отвлечь самых любознательных и пустить их по пути единичного случая (коим и являлось первое крякми), т.е. если бы им дали (как сейчас) еще одно крякми, но с другим алгоритмом, им бы пришлось придумывать новый способ поиска «нулей» и «единиц», что похоже со многими и произошло ;)
Ну да ладно, меньше слов больше дела.
Вот магическое «заклинание», которое поможет найти все нулевые и единичные символы:

Рис. 14
Хорошо у нас есть группа элементов дающих «нули» и «единицы». Как получить искомую таблицу [1, 0, 0, 0, 1, 0, 0, 0, 1]?
Самые внимательные/догадливые могли заметить (например, по комментариям к предыдущей статье), что мы имеем дело с матрицами, которые при умножении друг на друга должны давать единичную матрицу [1, 0, 0, 0, 1, 0, 0, 0, 1]. Следовательно, для получения единичной матрицы нам нужно либо две единичные матрицы, либо две обратные.
Чтобы получить требуемую единичную матрицу, можно использовать следующий паттерн:
Где в место y – подставьте любой единичный символ, а вместо x – любой нулевой.
Можно использовать и другие паттерны, найти их можно с помощью следующего «заклинания»:

Рис. 15
Произведя замену, можно получить, например, такие паттерны:
Теперь, когда мы разобрались с получением искомой единичной матрицы (т.е. таблицы валидации), перейдем к другим проблемам.
Мы знаем следующее:
Откуда следует, что, например, part_a зависит от part_1 и salt. Что в свою очередь, сужает возможные комбинации для part_a. Возникает закономерный вопрос.
Думаю многие уже догадались что нужно сделать? Правильно, использовать очередное «заклинание»!
Вот одно из них:
Если ваше «заклинание» успешно отработает, вы увидите, что для part_a и part_b доступно всего 4096 вариантов (точнее говоря «под вариантов»).

Рис. 16
Итак, теперь у нас есть все данные для генерации первого валидного ключа. Конечно, не стоит забывать, что мы работаем с байтами, которые имеют внутреннее представление, а значит прежде чем вводить их в окно крякми, их еще придется привести к нормальному виду.
Если вы были внимательны, то наверняка заметили, что все 4096 вариантов можно разделить на две группы, те у которых «все элементы четные» и те у которых «все элементы не четные».
index: 0035, table: [116, 222, 172] <= Все элементы четные
index: 0560, table: [172, 116, 222] <= Все элементы четные
index: 0770, table: [222, 172, 116] <= Все элементы четные
index: 0117, table: [1, 229, 111] <= Все элементы не четные
index: 1287, table: [229, 111, 1] <= Все элементы не четные
index: 1872, table: [111, 1, 229] <= Все элементы не четные
Однако, если вы посмотрите на доступные нам «паттерны», то увидите, что все они требуют того, чтобы в каждом из «вариантов» были как «четные», так и «не четные» элементы, т.е:
Вот две матрицы, которые дают нам единичную:
part_a
[176, 176, 65] <= Есть четные и не четные
[176, 65, 176] <= Есть четные и не четные
[65, 176, 176] <= Есть четные и не четные
part_b
[176, 176, 65] <= Есть четные и не четные
[176, 65, 176] <= Есть четные и не четные
[65, 176, 176] <= Есть четные и не четные
valid_table = part_a * part_a
[ 1, 0, 0 ]
[ 0, 1, 0 ]
[ 0, 0, 1 ]
Так как «варианты» с «четными» и «не четными» элементами отсутствуют – приходим к выводу, что в крякми находится ошибка. В стает закономерный вопрос.
После быстрых размышлений приходим к выводу, что ошибка кроется в фиксированной матрице [0x3, 0x5, 0x7, 0x5, 0x7, 0x3, 0x7, 0x3, 0x5]. Для получения четных и нечетных «вариантов» необходимо заменить «0x3», «0x5» и «0x7» на «0x2», «0x3» и «0x8» соответственно, либо на другой вариант, где будет два четных и один не четный элемент, например, на такие «0x4», «0x7» и «0x8» (как вариант).
Об этой ошибке было сообщено в Лабораторию Касперского. Там сказали, что та версия (которую мы сейчас исследуем) является черновой. После чего, в тот же день, всем была разослана версия без ошибки. Правда, в новой версии, уже не было фиксированных таблиц и решалась она еще проще чем эта, но об этом я расскажу чуть позже в бонусном разделе :)
Чтобы убедиться в том, что вы выполнили правильную замену (например, если вы решили вставить другие символы отличные от «0x2», «0x3» и «0x8»), следует использовать следующее «заклинание»:
Если приманка была подобрана правильно (как в нашем случае, «0x2, 0x3, 0x8»), то в ваших ловушках (в поле «Good») окажется, как минимум, один зверь (группа состоящая из трёх массивов). Пример вывода для фиксированной матрицы (с элементами «0x2», «0x3» и «0x8») показан ниже:

Рис. 17
Как видите, нам улыбнулась удача, поэтому в наши капканы попало целых три диких зверя, что конечно же будет способствовать сервировке праздничного стола (т.е. может использоваться для формирования part_a и part_b).
Самые внимательные уже заметили, что вывод в строке «Good» можно разбить на группы, в каждой из которой будет по три строки.
[0, 144, 81]
[81, 0, 144]
[144, 81, 0]
[144, 145, 0]
[0, 144, 145]
[145, 0, 144]
[0, 144, 209]
[209, 0, 144]
[144, 209, 0]
Еще более внимательные наверняка заметили, что все эти символы входят в наборы «нулевых» и «единичных» символов ;)

Рис. 18
Ну, а самые догадливые (я надеюсь) уже во всю пируют за большим столом, так как они смогли выследить большого зверя, приманив его подобным «заклинанием»:
На этом мы и закончим решать этот крякми… Как перевести внутренние байты в нормальный вид, чтобы их можно было ввести в окно крякми, я думаю разберетесь сами.
А пока вы разбираетесь мы перейдем к рассмотрению нового (исправленного) крякми. Сразу хочу сказать, что все что мы рассмотрели для данного крякми, актуально и для нового, поэтому ограничимся поверхностным описанием принципа его работы и дадим ссылку на кейген (для более любознательных или наоборот ленивых).
Дабы не запутаться с имеющимися версиями – внесем некоторую ясность в их нумерацию:
Как и во всех предшествующих версиях v1 и v2.
Как и в черновой версии v2 (рассматривался выше в этой статье).
Принцип действия такой же, как и в самой первой версии v1, но используются другие микшеры.
Как и во всех предшествующих версиях v1 и v2.
Крякми версий v2 и v3 можно найти в этой теме. Там же найдете кейген для новой версии v3 от меня Дарвина.
Пароль на архив от кейгена: Darwin_1iOi7q7IQ1wqWiiIIw
Проверка кейгена для третьей версии крякми:
> keygen_v3.py habrahabr.ru > result.txt
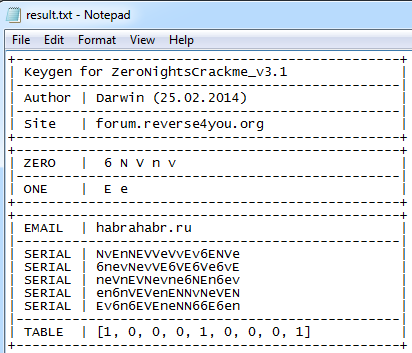
Рис. 19
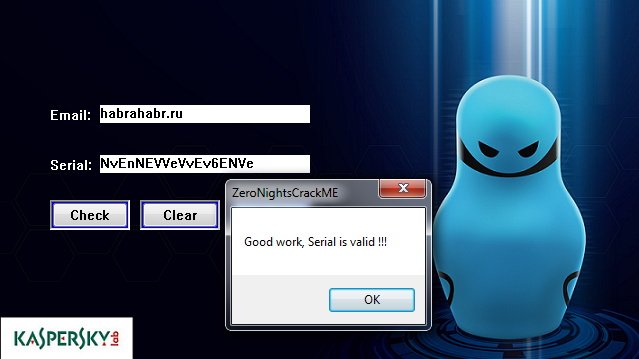
Рис. 20
Всем дочитавшим до конца огромное спасибо! До скорых встреч!
17 февраля пришло письмо с новым крякми. Именно о его решении (и не только) я и поведаю в этой статье.
Параметры крякми те же:
- Файл: ZeroNightsCrackMe.exe
- Платформа: Windows 7 (64 bit)
- Упаковщик: Отсутствует
- Антиотладка: Не натыкался
- Решение: Валидная пара Mail / Serial
Инструменты:
- OllyDbg 2.01
- Немного серого вещества
Приступим к решению…
Выходим на охоту
Как обычно запускаем подопытного и проводим поверхностный анализ. Реакция аналогична прошлому крякми.

Рис. 1
Зная принцип работы прошлого крякми, приступим к поиску ключевых моментов и найдем:
- Функцию занимающуюся обработкой введенных данных.
- Алгоритм проверки таблицы валидации.
- Таблицу валидации.
- Алгоритм заполнения таблицы валидации.
- Данные для алгоритма заполнения таблицы валидации.
- Алгоритм превращения серийного кода во внутреннее представление.
- Таблицу преобразования.
- Допустимый диапазон символов.
После чего сравним все ключевые моменты с предыдущей версией и найдем отличия.
По звериным тропам
Функция обработки введенных данных
Первым делом найдем функцию обработки введенных данных. Делается это довольно просто. Жмем правой кнопкой мыши в окне дизассемблера и выбираем «Search for => All referenced strings»:

Рис. 2
Далее жмем по строке «Good work, Serial is valid !!!» и попадаем сюда:

Рис. 3
Выше и будет находиться искомая функция (в моем случае это CALL 0x9b12b0). Ей передается три параметра. В Arg2, Arg1 передается размер серийного кода и указатель на серийный код соответственно, а в регистре ECX указатель на email.
Алгоритм проверки таблицы валидации
Заходим внутрь функции и крутим в самый низ, там находится алгоритм проверки таблицы валидации (идентичный старой версии):

Рис. 4
Адрес таблицы валидации
Ставим брейкпойнт в начале алгоритма и запускаем крякми на выполнение (разумеется, предварительно введя любые данные и нажав кнопку Check).

Рис. 5. Вводим тестовые данные

Рис. 6. Остановка на таблице валидации
Теперь определим адрес самой таблицы. Сделать это можно перейдя на строку «CMP DWORD PTR SS:[ECX*4+EBP-28],1» и подсмотрев целевой адрес.

Рис. 7. Определение адреса таблицы валидации
В моем случае адресом таблицы является 0x36f308 (выделено красным).

Рис. 8. Дамп таблицы валидации
Алгоритм заполнения таблицы валидации
Поиск алгоритма производим тем же способом, который был продемонстрирован при решении прошлого крякми, а именно:
- Продолжаем выполнение крякми (жмем F9 в Ольке);
- Ставим бряк на функцию обработки введенных данных, в моем случае это CALL 9b12b0 (рис. 3);
- Переключаемся на крякми и во всплывшем окне (говорящем об успешности или не успешности) нажимаем «Ок» (тем самым продолжая работу крякми);
- Далее жмем кнопку «Check» для запуска пересчета серийника, после чего вы должны остановиться на вызове CALL 0x9b12b0;
- Стоя на вызове CALL 0x9b12b0, поставьте бряк на запись, на адрес 0x36f308;
- И снова жмите F9.
Если все было сделано правильно, окажетесь здесь:

Рис. 9. Алгоритм заполнения таблицы валидации
Если сравните новый алгоритм со старым, то заметите, что они отличаются:

Рис. 10. Старый алгоритм (скриншот из прошлой статьи)
Представление «нового алгоритма» на Питоне выглядит следующим образом:
def create_table(first_part, second_part):
result = []
curr_second = 0
out_index = 0
while(out_index < 3):
inner_index = 0
while(inner_index < 3):
curr_first = 0
accumulator = 0
index = 0
while(index < 3):
first = first_part[inner_index + curr_first]
second = second_part[index + curr_second]
hash = 0
if (first != 0):
while (first != 0):
if (first & 1):
hash ^= second
second += second
first = first >> 1
accumulator ^= hash
index += 1
curr_first += 3
result.append(accumulator & 0xff)
inner_index += 1
out_index += 1
curr_second += 3
return resultПерейдем к поиску данных которые используются этим алгоритмом.
Данные для алгоритма заполнения таблицы валидации
Проанализировав код алгоритма было обнаружено два места, откуда берутся данные для его работы:

Рис. 11. Массивы с которыми оперирует новый алгоритм
Выше они выделены серым прямоугольником. В моем случае, по адресам 0x9b11b0 и 0x9b11b2, идет обращение к следующим массивам:
- 0x00758628 (рис. 12)
- 0x00758908 (рис. 13)

Рис. 12

Рис. 13
В каждом массиве находится 9 элементов по одному байту.
Если бы мы решали старый крякми, то мы бы сейчас перешли к поиску алгоритма превращения серийного кода во внутреннее представление, но в новом крякми было обнаружено существенное отличие от поведения старого крякми, поэтому ниже дана информация об отличиях, которые заключается вот в чём.
Отличие старой версии от новой
В старой версии крякми работа с серийным кодом происходила следующим образом:
- Серийный код разбивался на две части.
- Каждая часть переводилась во внутреннее представление.
- Затем каждая часть микшировалась (перемешивалась).
- После чего обе части передавались алгоритму заполнения таблицы валидации.
В итоге у нас получалось что-то вроде этого:
Serial
|- part_1
|- part_2
part_1 = intermediate_view(part_1)
part_2 = intermediate_view(part_2)
part_1 = mix(part_1)
part_2 = mix(part_2)
valid_table = algo(part_1, part_2)В новой же версии всё немного усложнилось:
- Серийный код разбивается на две части.
- Каждая его часть переводится во внутренне представление.
- Первая часть + фиксированный массив (3, 5, 7, 5, 7, 3, 7, 3, 5) передается в алгоритм.
- Вторая часть + фиксированный массив (3, 5, 7, 5, 7, 3, 7, 3, 5) передается в алгоритм.
- Результат пунктов 3-4 передается в алгоритм заполнения таблицы валидации.
В итоге получаем что-то вроде этого:
Serial
|- part_1
|- part_2
part_1 = intermediate_view(part_1)
part_2 = intermediate_view(part_2)
part_1 = mix(part_1)
part_2 = mix(part_2)
salt = [3, 5, 7, 5, 7, 3, 7, 3, 5]
part_a = algo(part_1, salt)
part_b = algo(part_2, salt)
valid_table = algo(part_a, part_b)Откуда следует, что у нас появляется зависимость от фиксированного массива.
Алгоритм превращения серийного кода во внутреннее представление
Поиск конвертера серийного кода я оставлю за вами и здесь приводить не буду. Поиск можно осуществлять тем же способом, что и в старой версии.
Таблица преобразования и допустимый диапазон
Таблица и допустимый диапазон идентичны старой версии.
Готовим лежбище для засады
Теперь когда все необходимые элементы были собраны можно приступать к решению.
Алгоритм наших действий следующий:
- Для algo(part_a, part_b), найти такие part_a и part_b, которые дают результат [1, 0, 0, 0, 1, 0, 0, 0, 1]
- Для part_a = algo(part_1, salt), найти такой part_1, который даст результат равный part_a.
- Для part_b = algo(part_2, salt), найти такой part_2, который даст результат равный part_b.
Начнем с algo(part_a, part_b)
Если вы читали первую статью, то наверное помните, что для составления требуемой таблицы [1, 0, 0, 0, 1, 0, 0, 0, 1], необходимо иметь такие байты, которые бы при взаимодействии друг с другом давали либо «нули», либо «единицы».
В старой версии крякми найти эти байты было очень просто. Всё что нужно было сделать это перебрать весь доступный алфавит и применить к нему несколько простых операций.
В новой версии это сделать намного сложнее (но это только на первый взгляд и ниже я объясню почему). В старой версии мы могли перебирать по одному элементу. В новой версии мы должны перебирать по три элемента, так как все они взаимно связаны.
И так, почему же новая версия кажется сложной, но только на первый взгляд?
Потому что в первой статье я не раскрыл ту «магию», которая в действительности была скрыта за поиском «нулей» и «единиц» (в этой статье её придется раскрыть, хотя можно было этого не делать). В своём кейгене я использовал функцию, которая ищет требуемые «нули» и «единицы», но не совсем очевидным способом. Это помогло успешно отвлечь самых любознательных и пустить их по пути единичного случая (коим и являлось первое крякми), т.е. если бы им дали (как сейчас) еще одно крякми, но с другим алгоритмом, им бы пришлось придумывать новый способ поиска «нулей» и «единиц», что похоже со многими и произошло ;)
Ну да ладно, меньше слов больше дела.
Вот магическое «заклинание», которое поможет найти все нулевые и единичные символы:
data_zero, data_ones = [], []
for a in range(0, 256):
part_a = [a, a, a, a, a, a, a, a, a]
part_b = [a, a, a, a, a, a, a, a, a]
result = create_table(part_a, part_b)
if result == [0, 0, 0, 0, 0, 0, 0, 0, 0]:
data_zero.append(a)
elif result == [1, 1, 1, 1, 1, 1, 1, 1, 1]:
data_ones.append(a)
print("ZERO:", data_zero)
print("ONES:", data_ones)
Рис. 14
Хорошо у нас есть группа элементов дающих «нули» и «единицы». Как получить искомую таблицу [1, 0, 0, 0, 1, 0, 0, 0, 1]?
Самые внимательные/догадливые могли заметить (например, по комментариям к предыдущей статье), что мы имеем дело с матрицами, которые при умножении друг на друга должны давать единичную матрицу [1, 0, 0, 0, 1, 0, 0, 0, 1]. Следовательно, для получения единичной матрицы нам нужно либо две единичные матрицы, либо две обратные.
Чтобы получить требуемую единичную матрицу, можно использовать следующий паттерн:
# Паттерн
part_a = [y, x, x, x, y, x, x, x, y]
part_b = [y, x, x, x, y, x, x, x, y]
result = algo(part_a, part_b)Где в место y – подставьте любой единичный символ, а вместо x – любой нулевой.
Можно использовать и другие паттерны, найти их можно с помощью следующего «заклинания»:
happy = [1,32]
for byte_1 in happy:
for byte_2 in happy:
for byte_3 in happy:
for byte_4 in happy:
for byte_5 in happy:
for byte_6 in happy:
for byte_7 in happy:
for byte_8 in happy:
for byte_9 in happy:
part_1 = [byte_1, byte_2, byte_3, byte_4, byte_5, byte_6, byte_7, byte_8, byte_9]
part_2 = [byte_1, byte_2, byte_3, byte_4, byte_5, byte_6, byte_7, byte_8, byte_9]
result = create_table(part_1, part_2)
if result == [1, 0, 0, 0, 1, 0, 0, 0, 1]:
print("%s | %s " % (part_2, part_1))
Рис. 15
Произведя замену, можно получить, например, такие паттерны:
patterns = [
# Pattern 0
[
[y1, x1, x1, x1, y2, x1, x1, x1, y3],
[y1, x1, x1, x1, y2, x1, x1, x1, y3]
],
# Pattern 1a
[
[y1, x1, x1, x1, x1, y1, x1, y1, x1],
[y1, x1, x1, x1, x1, y1, x1, y1, x1]
],
# Pattern 1b
[
[y1, x1, x2, x3, x4, y1, x5, y1, x6],
[y1, x2, x1, x5, x6, y1, x3, y1, x4]
],
# Pattern 2a
[
[y1, x1, x1, x1, y1, x1, x1, x1, y1],
[y1, x1, x1, x1, y1, x1, x1, x1, y1]
],
# Pattern 2b
[
[y1, x1, x2, x3, y2, x4, x5, x6, y3],
[y1, x1, x2, x3, y2, x4, x5, x6, y3]
],
# Pattern 3a
[
[x1, x1, y1, x1, y1, x1, y1, x1, x1],
[x1, x1, y1, x1, y1, x1, y1, x1, x1]
],
# Pattern 3b
[
[x1, x2, y1, x3, y2, x4, y3, x5, x6],
[x6, x5, y3, x4, y2, x3, y1, x2, x1]
],
# Pattern 4a
[
[x1, y1, x1, y1, x1, x1, x1, x1, y1],
[x1, y1, x1, y1, x1, x1, x1, x1, y1]
],
# Pattern 4b
[
[x1, y1, x2, y2, x3, x4, x5, x6, y3],
[x3, y2, x4, y1, x1, x2, x6, x5, y3]
],
# Pattern 5
[
[x1, x2, y1, y2, x3, x4, x5, y3, x6],
[x4, y2, x3, x6, x5, y3, y1, x1, x2]
]
]Теперь, когда мы разобрались с получением искомой единичной матрицы (т.е. таблицы валидации), перейдем к другим проблемам.
Как подобрать подходящие part_a и part_b?
Мы знаем следующее:
part_a = algo(part_1, salt)
part_b = algo(part_2, salt)
valid_table = algo(part_a, part_b)Откуда следует, что, например, part_a зависит от part_1 и salt. Что в свою очередь, сужает возможные комбинации для part_a. Возникает закономерный вопрос.
Какие комбинации мы можем использовать?
Думаю многие уже догадались что нужно сделать? Правильно, использовать очередное «заклинание»!
Вот одно из них:
# serial_data для email “support@reverse4you.org”
serial_data = [52, 233, 91, 105, 65, 15, 50, 176, 90, 40, 225, 81, 207, 79, 34, 19]
def get_items(first_part, second_part):
result = []
inner_index = 0
while(inner_index < 3):
curr_first = 0
accumulator = 0
index = 0
while(index < 3):
first = first_part[inner_index + curr_first]
second = second_part[index]
hash = 0
if (first != 0):
while (first != 0):
if (first & 1):
hash ^= second
second += second
first = first >> 1
accumulator ^= hash
index += 1
curr_first += 3
result.append(accumulator & 0xff)
inner_index += 1
return result
a = 0x3
b = 0x5
c = 0x7
first_part = [a, b, c, b, c, a, c, a, b]
second_part_new = [0, 0, 0]
count = 0
result_table = []
for byte_1 in serial_data:
second_part_new[0] = byte_1
for byte_2 in serial_data:
second_part_new[1] = byte_2
for byte_3 in serial_data:
second_part_new[2] = byte_3
res = get_items(first_part, second_part_new)
print("index: %s, table: %s" % (count, res))
count += 1
print("Count: %s" % count)Если ваше «заклинание» успешно отработает, вы увидите, что для part_a и part_b доступно всего 4096 вариантов (точнее говоря «под вариантов»).

Рис. 16
Итак, теперь у нас есть все данные для генерации первого валидного ключа. Конечно, не стоит забывать, что мы работаем с байтами, которые имеют внутреннее представление, а значит прежде чем вводить их в окно крякми, их еще придется привести к нормальному виду.
Первая жертва (первый валидный ключ)
Если вы были внимательны, то наверняка заметили, что все 4096 вариантов можно разделить на две группы, те у которых «все элементы четные» и те у которых «все элементы не четные».
index: 0035, table: [116, 222, 172] <= Все элементы четные
index: 0560, table: [172, 116, 222] <= Все элементы четные
index: 0770, table: [222, 172, 116] <= Все элементы четные
index: 0117, table: [1, 229, 111] <= Все элементы не четные
index: 1287, table: [229, 111, 1] <= Все элементы не четные
index: 1872, table: [111, 1, 229] <= Все элементы не четные
Однако, если вы посмотрите на доступные нам «паттерны», то увидите, что все они требуют того, чтобы в каждом из «вариантов» были как «четные», так и «не четные» элементы, т.е:
Вот две матрицы, которые дают нам единичную:
part_a
[176, 176, 65] <= Есть четные и не четные
[176, 65, 176] <= Есть четные и не четные
[65, 176, 176] <= Есть четные и не четные
part_b
[176, 176, 65] <= Есть четные и не четные
[176, 65, 176] <= Есть четные и не четные
[65, 176, 176] <= Есть четные и не четные
valid_table = part_a * part_a
[ 1, 0, 0 ]
[ 0, 1, 0 ]
[ 0, 0, 1 ]
Так как «варианты» с «четными» и «не четными» элементами отсутствуют – приходим к выводу, что в крякми находится ошибка. В стает закономерный вопрос.
В чем заключается ошибка?
После быстрых размышлений приходим к выводу, что ошибка кроется в фиксированной матрице [0x3, 0x5, 0x7, 0x5, 0x7, 0x3, 0x7, 0x3, 0x5]. Для получения четных и нечетных «вариантов» необходимо заменить «0x3», «0x5» и «0x7» на «0x2», «0x3» и «0x8» соответственно, либо на другой вариант, где будет два четных и один не четный элемент, например, на такие «0x4», «0x7» и «0x8» (как вариант).
Об этой ошибке было сообщено в Лабораторию Касперского. Там сказали, что та версия (которую мы сейчас исследуем) является черновой. После чего, в тот же день, всем была разослана версия без ошибки. Правда, в новой версии, уже не было фиксированных таблиц и решалась она еще проще чем эта, но об этом я расскажу чуть позже в бонусном разделе :)
Чтобы убедиться в том, что вы выполнили правильную замену (например, если вы решили вставить другие символы отличные от «0x2», «0x3» и «0x8»), следует использовать следующее «заклинание»:
serial_data = [52, 233, 91, 105, 65, 15, 50, 176, 90, 40, 225, 81, 207, 79, 34, 19]
a = 0x2
b = 0x3
c = 0x8
first_part = [a, b, c, b, c, a, c, a, b]
second_part_new = [0, 0, 0]
count = 0
result_table = []
for byte_1 in serial_data:
second_part_new[0] = byte_1
for byte_2 in serial_data:
second_part_new[1] = byte_2
for byte_3 in serial_data:
second_part_new[2] = byte_3
res = get_items(first_part, second_part_new)
print("index: %s, table: %s" % (count, res))
if (res[0] % 16 == 0 and res[1] % 16 == 0 and res[2] % 16 == 1) or\
(res[0] % 16 == 1 and res[1] % 16 == 0 and res[2] % 16 == 0) or\
(res[0] % 16 == 0 and res[1] % 16 == 1 and res[2] % 16 == 0):
result_table.append(res)
count += 1
print("Count:", count)
print("Good:", result_table)Если приманка была подобрана правильно (как в нашем случае, «0x2, 0x3, 0x8»), то в ваших ловушках (в поле «Good») окажется, как минимум, один зверь (группа состоящая из трёх массивов). Пример вывода для фиксированной матрицы (с элементами «0x2», «0x3» и «0x8») показан ниже:

Рис. 17
Как видите, нам улыбнулась удача, поэтому в наши капканы попало целых три диких зверя, что конечно же будет способствовать сервировке праздничного стола (т.е. может использоваться для формирования part_a и part_b).
Самые внимательные уже заметили, что вывод в строке «Good» можно разбить на группы, в каждой из которой будет по три строки.
[0, 144, 81]
[81, 0, 144]
[144, 81, 0]
[144, 145, 0]
[0, 144, 145]
[145, 0, 144]
[0, 144, 209]
[209, 0, 144]
[144, 209, 0]
Еще более внимательные наверняка заметили, что все эти символы входят в наборы «нулевых» и «единичных» символов ;)

Рис. 18
Ну, а самые догадливые (я надеюсь) уже во всю пируют за большим столом, так как они смогли выследить большого зверя, приманив его подобным «заклинанием»:
# Характеристика зверя
# [0, 144, 209]
# [209, 0, 144]
# [144, 209, 0]
a = 144
b = 209
c = 0
# Применяем один из доступных паттернов
part_a = [c, a, b, b, c, a, a, b, c]
part_b = [a, b, c, c, a, b, b, c, a]
# part_a1 = [0, 144, 209]
# part_a2 = [209, 0, 144]
# part_a3 = [144, 209, 0]
# part_a = part_a1 + part_a2 + part_a3
# part_b1 = [144, 209, 0]
# part_b2 = [0, 144, 209]
# part_b3 = [209, 0, 144]
# part_b = part_b1 + part_b2 + part_b3
result = create_table(part_a, part_b)
print(result)На этом мы и закончим решать этот крякми… Как перевести внутренние байты в нормальный вид, чтобы их можно было ввести в окно крякми, я думаю разберетесь сами.
А пока вы разбираетесь мы перейдем к рассмотрению нового (исправленного) крякми. Сразу хочу сказать, что все что мы рассмотрели для данного крякми, актуально и для нового, поэтому ограничимся поверхностным описанием принципа его работы и дадим ссылку на кейген (для более любознательных или наоборот ленивых).
Бонус (кейген + описание работы нового крякми)
Дабы не запутаться с имеющимися версиями – внесем некоторую ясность в их нумерацию:
- ZeroNightsCrackMe_v1 – рассмотрен здесь.
- ZeroNightsCrackMe_v2 – является черновой версией и описан выше в этой статье.
- ZeroNightsCrackMe_v3 – поверхностно рассмотрен ниже + дается кейген.
Алгоритм проверки таблицы валидации и сама таблица валидации
Как и во всех предшествующих версиях v1 и v2.
Алгоритм заполнения таблицы валидации
Как и в черновой версии v2 (рассматривался выше в этой статье).
Данные для алгортима заполнения таблицы валидации
Принцип действия такой же, как и в самой первой версии v1, но используются другие микшеры.
Алгоритм превращения серийного кода во внутреннее представление, таблица преобразования и допустимый диапазон
Как и во всех предшествующих версиях v1 и v2.
Кейген для новой версии
Крякми версий v2 и v3 можно найти в этой теме. Там же найдете кейген для новой версии v3 от меня Дарвина.
Пароль на архив от кейгена: Darwin_1iOi7q7IQ1wqWiiIIw
Проверка кейгена для третьей версии крякми:
> keygen_v3.py habrahabr.ru > result.txt

Рис. 19

Рис. 20
Всем дочитавшим до конца огромное спасибо! До скорых встреч!