aprlv 28 авг 2015 в 11:20

Минимализм в криптографии, или схема Even–Mansour

15 мин

17K

Информационная безопасность*Криптография*Математика*

Израильские ученые Шимон Ивэн (Shimon Even) и Ишай Мансур (Yishay Mansour) еще в 1997 году задались вопросом: насколько минимальной конструкцией может обладать стойкий блочный шифр? Под минимальностью они подразумевали число конструктивных элементов в схеме шифра, а под стойкостью — любую (формально верную) оценку снизу сложностей атак на этот шифр. Как говорится, под катом — описание минимального (и по сей день) блочного шифра с доказуемой стойкостью.

Лирическое отступление

~~Практически~~ все стандарты шифрования, используемые сегодня, не являются формально стойкими. Никто не дает, и не может дать никаких гарантий, что в них нет закладок, уязвимостей или слабостей. Просто до сих никто не придумал (или, по крайней мере, не опубликовал) никаких способов взломать эти шифры = способов существенно снизить экспоненциальную сложность полного перебора. Вскрытие ~~практически~~ любых криптографических алгоритмов, на которых зиждятся ваши безопасность и конфиденциальность, будь то симметричное, асимметричное шифрование, или хэширование, сводится к решению относительно сложных задач (например, к задаче дискретного логарифмирования). Сложных потому, что относительно простых решений до сих пор никто не предложил. Пока мы не научимся логарифмировать в конечном поле или разлагать числа на множители за полиномиальное время (или пока не построим квантовый компьютер побольше), DH и RSA будут считаться стойкими, и только число бит в ключе будет расти пропорционально мощности персональных компьютеров.

А все потому, что мы пока не умеем получать оценок снизу. Друзья, в математике (и особенно в криптографии) не так много красивых идей и изящных решений, а доказанных оценок снизу — еще меньше. Рассмотренный здесь шифр, на мой взгляд, попадает в пересечение: он максимально прост, и в то же время формально стоек.

Предупреждаю сразу, что эта публикация — не художественное произведение для неподготовленных читателей, хотя и не содержит ничего более сложного, чем формулу условной вероятности Байеса и элементарную арифметику дробей. Неискушенный читатель останется удовлетворенным и описанием конструкции шифра, а строгое доказательство его стойкости приведено здесь для специалистов и истинных ценителей математики.

Израильские ученые Шиман Ивэн (Shimon Even) и Ишэй Мансур (Yishay Mansour) в [EM97] предложили способ построить блочный шифр, обладающий доказуемой стойкостью, на основе единственной случайно выбранной подстановки из $S_{2n}$ .

Прежде, чем я познакомлю вас непосредственно с этим блочным шифром, позволю себе указать список введенных условных обозначений и базовых определений. Впрочем, вы всегда сможете к нему вернуться, поэтому, в том случае, если мне удалось пробудить в вас нешуточный интерес увидеть все «здесь и сейчас», переходите непосредственно к описанию шифра.

Определения и условные обозначения

Множества, наборы

$\left\lbrace A, B, C, \dots \right\rbrace$ — неупорядоченное множество элементов $A, B, C, \dots$
$\left\langle A, B, C, \dots \right\rangle$ — упорядоченное множество элементов $A, B, C, \dots$

Начертания

$\mathcal{P}, \mathcal{C}, \mathcal{K}$ — пространства, используемые криптосистемами
$\mathrm{A}, \mathrm{B}$ — алгоритмы, модели вычислений
$\mathrm{E}, \mathrm{P}, \mathrm{D}$ — оракулы
$\mathsf{E}, \mathsf{P}$ — множества, выработанные алгоритмами
$\pi, \sigma, \delta$ — подстановки
$\mathsf{CP}, \mathsf{EFP}$ — задачи

Обозначения

$\mathcal{P}$ — множество открытых текстов (сообщений)
$\left\lbrace P_1, P_2, \dots\right\rbrace \subseteq \mathcal{P}$ — открытые тексты $P_1, P_2, \dots$
$\mathcal{C}$ — множество шифртекстов (криптограмм)
$\left\lbrace C_1, C_2, \dots\right\rbrace \subseteq \mathcal{C}$ — шифртексты $C_1, C_2, \dots$
$\mathcal{K}$ — множество ключей
$\left\lbrace K_1, K_2, \dots\right\rbrace \subseteq \mathcal{K}$ — ключи $K_1, K_2, \dots$
$\underline{K} \in \mathcal{K}$ — истинный ключ
$E \colon \mathcal{P} \times \mathcal{K} \mapsto \mathcal{C}$ — функция шифрования
$D \colon \mathcal{C} \times \mathcal{K} \mapsto \mathcal{P}$ — функция расшифрования
$\mathrm{P}_{\sigma}, \mathrm{P}_{\sigma}^{-1}$ — оракулы, реализующие подстановки $\sigma, \sigma^{-1}$
$\mathrm{E}_{K, \sigma}, \mathrm{D}_{K, \sigma}$ — оракулы, реализующие функции $E, D$ на ключе $K$
$p_{\mathrm{A}}$ — вероятность успеха алгоритма $\mathrm{A}$
$T_{\mathrm{A}}$ — время выполнения алгоритма $\mathrm{A}$

Определения

Криптосистемой $S$ называется упорядоченная пятерка множеств $S = \left\langle \mathcal{P}, \mathcal{C}, \mathcal{K}, E, D \right\rangle$ , где

$\mathcal{P}$ — множество открытых текстов (plaintexts),
$\mathcal{C}$ — множество шифртекстов (ciphertexts),
$\mathcal{K}$ — множество ключей (keys),
$E$ — (инъективная) функция шифрования (encipher):

$E \colon \mathcal{P} \times \mathcal{K} \mapsto \mathcal{C}; \quad \forall K \in \mathcal{K} \implies E_K \colon \mathcal{P} \mapsto \mathcal{C};$

$D$ — функция расшифрования (decipher):

$D \colon \mathcal{C} \times \mathcal{K} \mapsto \mathcal{P}; \quad \forall K \in \mathcal{K} \implies D_K \colon \mathcal{C} \mapsto \mathcal{P}.$

Классическая схема Even–Mansour

Израильские ученые Шимон Ивэн (Shimon Even) и Ишай Мансур (Yishay Mansour) в своей работе предложили блочный шифр c доказуемой криптостойкостью, для которого требуется всего одна подстановка $\pi$ , которая случайным (или псевдослучайным) образом выбирается из множества всех перестановок $S_{2^n}$ над открытыми текстами.

При этом предполагается, что выбранная подстановка не является частью ключа, и доступна любому атакающему в виде некоторого «черного ящика».

Утверждается, что, с точки зрения атакующего, предложенный шифр практически неотличим от идеального случайного шифра, и вероятность успешного вскрытия системы (восстановления секретного ключа $\underline{K}$ ) полиномиально мала (основной результат — Теорема 2, Следствие 2.1 из нее, и Теорема 3).

Утверждается также, что использование псевдослучайной подстановки вместо истинно случайной подстановки не изменяет показанной стойкости шифра.

Описание

Пусть $\mathcal{P} \equiv \mathcal{C}$ , и $\pi \in S_{\left\vert\, {\mathcal{P} \,\right\vert}$ — подстановка, выбранная из множества $S_{\left\vert\, {\mathcal{P} \,\right\vert}$ всех подстановок над множеством открытых текстов, а $\pi^{-1}$ — обратная к ней.

Предполагается, что для любых элементов $P \in \mathcal{P}$ и $C \in \mathcal{C}$ множеств открытых и шифртекстов значения $\pi(P)$ и $\pi^{-1} (C)$ могут быть легко получены либо с помощью непосредственного вычисления значения подстановок $\pi$ и $\pi^{-1}$ , либо посредством обращения к общедоступным оракулам $\mathrm{P}_{\pi}$ и $\mathrm{P}^{-1}_{\pi}$ .

Пространства открытых и шифртекстов являются пространствами двоичных $n$ –мерных векторов: $\mathcal{P} \equiv \mathcal{C} = \left\lbrace 0, 1 \right\rbrace^n = \mathbb{Z}_{2}^{n}$ , а пространство ключей системы является пространством двоичных векторов размерности $2n$ : $\mathcal{K} = \left\lbrace 0,1 \right\rbrace^{2n} = \mathbb{Z}_{2}^{2n}$ .

Секретный ключ $\underline{K} \in \mathcal{K}$ является упорядоченной парой двух $n$ –мерных подключей (половин) $\underline{K}_1$ и $\underline{K}_2$ ; каждый подключ выбирается случайно из пространства $n$ –мерных двоичных векторов с равной вероятностью $2^{-n}$ .

Предполагается также, что выбранный секретный ключ $\underline{K}$ известен только легитимным пользователям, и используется ими для шифрования открытых текстов (сообщений) и расшифрования шифртекстов (криптограмм).

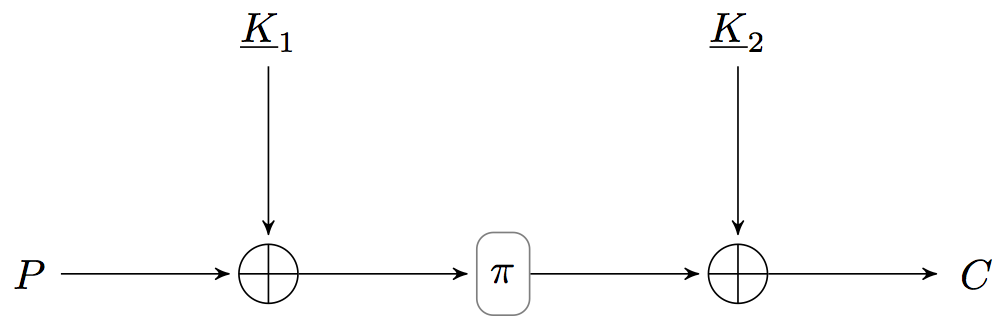
Шифрование открытого текста $P$ с помощью секретного ключа $\underline{K} = \left\langle \underline{K}_1, \underline{K}_2 \right\rangle$ и выбранной подстановки $\pi$ производится следующим образом:

$E_{\underline{K}} (P) = E(P, \left\langle \underline{K}_1, \underline{K}_2 \right\rangle) = \pi(P \oplus \underline{K}_1) \oplus \underline{K}_2,$

а расшифрование шифртекста $C$ с помощью ключа $K$ и выбранной подстановки $\pi$ — следующим:

$D_{\underline{K}} (C) = D(C, \left\langle \underline{K}_1, \underline{K}_2 \right\rangle) = \pi^{-1}(C \oplus \underline{K}_2) \oplus \underline{K}_1.$

Действительно, просто? Взяли сообщение, поксорили с первой половиной ключа, по открытой и доступной всем табличке заменили, поксорили со второй половиной ключа, и получилась криптограмма. Здорово, правда? Почему же никто не использует эту схему на практике? Ведь она намного проще AES, да и DES. Самый простой блочный шифр. Где здесь подвох?

Подвох

Все дело в том, подстановка задана на двоичных $n$ –битных векторах, и хранить таблицу замены для случайно выбранной подстановки совершенно неприемлимо, на это потребуется $\mathcal{O}\!\left(n 2^n\right)$ памяти. Единственно возможное решение этой проблемы заключается в том, чтобы строить хорошие псевдослучайные подстановки (полиномиально неотличимые от случайных), значения которых можно было бы относительно легко вычислить в любой точке; а это мы пока не умеем.

О минимальности схемы

Следует отметить, что классическая схема минимальна в том смысле, что удаление любого из элементов этой схемы приводит к значительному ослаблению ее стойкости. Легко показать, что удаление любого из сложений с подключами, либо подстановки $\pi$ сделает схему уязвимой, и, как следствие, совершенно нестойкой.

Отсутствует сложение с первым подключом.

Функция шифрования имеет вид:

$E (P, \underline{K}) = C = \pi(P) \oplus \underline{K}, \text{ где } \underline{K} \in \mathcal{K} \equiv \mathcal{P} = \mathbb{Z}_{2}^{n}.$

Злоумышленник может легко вычислить секретный ключ $\underline{K}$ , зная подстановку $\pi$ :

$\underline{K} = C \oplus \pi (P).$
Отсутствует сложение со вторым подключом.

Функция шифрования имеет вид:

$E (P, \underline{K}) = C = \pi(P \oplus \underline{K}), \text{ где } \underline{K} \in \mathcal{K} \equiv \mathcal{P} = \mathbb{Z}_{2}^{n}.$

Злоумышленник может легко вычислить секретный ключ $\underline{K}$ , зная подстановку $\pi^{-1}$ :

$\underline{K} = \pi^{-1} (C) \oplus P.$
Отсутствует $S$ –блок (подстановка $\pi$ )

Функция шифрования имеет вид:

$E (P, \underline{K}_1 \oplus \underline{K}_2) = C = P \oplus \underline{K}_1 \oplus \underline{K}_2.$

Злоумышленник может легко вычислить секретный ключ $\underline{K}$ :

$\underline{K} = \underline{K}_1 \oplus \underline{K}_2 = P \oplus C.$

О стойкости схемы

Предположения стойкости, определения

Стойкость предложенной схемы обусловлена следующими предположениями:

злоумышленнику не известен истинный ключ $\underline{K} \in \mathcal{K}$ ;
злоумышленник имеет возможность шифровать открытые тексты (сообщения) и расшифровывать шифртексты (криптограммы) на секретном ключе $\underline{K}$ ;
злоумышленник имеет возможность вычислять значения перестановки $\pi$ и обратной к ней перестановки $\pi^{-1}$ .

Всякий алгоритм, вскрывающий систему, может обращаться к следующим четырем оракулам $\mathrm{P}, \mathrm{P}^{-1}, \mathrm{E}, \mathrm{D}$ :

оракул $\mathrm{P}_{\pi}$ вычисляет значение перестановки $\pi \in S_{\left\vert\,\mathcal{P}\right\vert\,}$ на $n$ –мерном двоичном входном наборе $M$ :

$\mathrm{P}_{\pi} \colon \mathbb{Z}_{2}^{n} \mapsto \mathbb{Z}_{2}^{n}, \quad \operatorname{\mathrm{P}_{\pi}}\left[M\right]} = \pi (M);$

оракул $\mathrm{P}^{-1}_{\pi}$ вычисляет значение перестановки $\pi^{-1} \in S_{\left\vert\,\mathcal{P}\,\right\vert}$ на $n$ –мерном двоичном входном наборе $M'$ :

$\mathrm{P}^{-1}_{\pi} \colon \mathbb{Z}_{2}^{n} \mapsto \mathbb{Z}_{2}^{n}, \quad \operatorname{\mathrm{P}^{-1}_{\pi}}\left[M'\right]} = \pi^{-1} (M');$

оракул $\mathrm{E}_{\underline{K}, \pi}$ зашифровывает $n$ –мерный двоичный набор (открытый текст) $P$ на $2n$ –мерном ключе $\underline{K}$ :

$\mathrm{E}_{\underline{K}, \pi} \colon \mathcal{P} \equiv \mathbb{Z}_{2}^{n} \mapsto \mathcal{C} \equiv \mathbb{Z}_{2}^{n}, \quad \operatorname{\mathrm{E}_{\underline{K}, \pi}}\left[P\right]} = \underline{K}_2 \oplus \pi (P \oplus \underline{K}_1);$

оракул $\mathrm{D}_{\underline{K}, \pi}$ расшифровывает $n$ –мерный двоичный набор (шифртекст) $C$ на $2n$ –мерном ключе $\underline{K}$ :

$\mathrm{D}_{\underline{K}, \pi} \colon \mathcal{C} \equiv \mathbb{Z}_{2}^{n} \mapsto \mathcal{P} \equiv \mathbb{Z}_{2}^{n}, \quad \operatorname{\mathrm{D}_{\underline{K}, \pi}}\left[C\right]} = \underline{K}_1 \oplus \pi^{-1} (C \oplus \underline{K}_2).$

Далее, если подстановка, значение которой вычисляет оракул $\mathrm{P}_{\pi}$ ( $\mathrm{P}^{-1}_{\pi}$ ), выбрана, а шифрование и расшифрование осуществляется на фиксированном ключе $\underline{K}$ , то индекс у обозначений оракулов мы будем опускать: $\mathrm{P}, \mathrm{P}^{-1}, \mathrm{E}, \mathrm{D}$ .

Обращаясь к оракулам $\mathrm{P}$ и $\mathrm{P}^{-1}$ с запросами на вычисление значения подстановок $\pi$ и $\pi^{-1}$ в точках $M$ и $M' = \pi(M)$ , алгоритм получает ответы $M'$ и $M$ соответственно.
Таким образом, общение всякого алгоритма с оракулами $\mathrm{P}$ и $\mathrm{P}^{-1}$ сводится к формированию пар вида «точка», «значение подстановки $\pi$ в этой точке»:

$\left\langle M, M' \right\rangle = \left\langle M, \pi(M) \right\rangle.$

Назовем такие пары $P$ –парами, а набор всех $P$ –пар, выработанных некоторым алгоритмом $\mathrm{A}$ в результате его выполнения, обозначим через $\mathsf{P}_{\mathrm{A}}$ , или просто $\mathsf{P}$ .

Обращаясь к оракулам $\mathrm{E}$ и $\mathrm{D}$ с запросами на шифрование открытого текста $P$ и расшифрование шифртекста $C = E(P, \underline{K})$ , алгоритм получает ответы $C$ и $P$ соответственно.
Так, общение всякого алгоритма с оракулами $\mathrm{E}$ и $\mathrm{D}$ сводится к формированию пар вида «открытый текст», «шифртекст»:

$\left\langle P, C \right\rangle = \left\langle M, E(P, \underline{K \right\rangle)}.$

Назовем такие пары $E$ –парами, а набор всех $E$ –пар, выработанных некоторым алгоритмом $\mathrm{A}$ в результате его выполнения, обозначим через $\mathsf{E}_{\mathrm{A}}$ , или просто $\mathsf{E}$ .

Определение
$E$ –пары $\left\langle P_1, C_1 \right\rangle$ и $\left\langle P_2, C_2 \right\rangle$ называются пересекающимися, если $P_1 = P_2$ , либо $C_1 = C_2$ .

Аналогичное определение можно сформулировать и для $P$ –пар.

Определение
$P$ –пары $\left\langle M_1, M_1' \right\rangle$ и $\left\langle M_2, M_2' \right\rangle$ называются пересекающимися, если $M_1 = M_1'$ , либо $M_2 = M_2'$ .

Утверждение 1 (Overlapping pairs are identical)
Ввиду того, что все оракулы $\mathrm{P}_{\sigma}, \mathrm{P}^{-1}_{\sigma}, \mathrm{E}_{K, \sigma}, \mathrm{D}_{K, \sigma}$ честны, для любых фиксированных $\sigma$ и $K$ справедливы утверждения:

пересекающиеся $E$ –пары совпадают;
пересекающиеся $P$ –пары совпадают.

По модулю утверждения 1 можно полагать, что все пары множеств $\mathsf{E}$ и $\mathsf{P}$ не пересекаются между собой.

Вероятностью успеха $p_{\mathrm{A}}$ алгоритма $\mathrm{A}$ назовем вероятность вычисления этим алгоритмом $\mathrm{A}$ корректного выхода на произвольных (но корректных) входах. Так, например, вероятностью $p_{\mathrm{A}}$ успеха алгоритма $\mathrm{A}$ , вычисляющего ключ шифрования по $E$ –паре $\left\langle P, C \right\rangle$ , будет вероятность

$\forall P, C \>\Longrightarrow\> p_{\mathrm{A}} = \Pr{\operatorname{A}\left[\left\langle P, C \right\rangle\right]} = \underline{K}}.$

Под временем выполнения $T_{\mathrm{A}}$ алгоритма $\mathrm{A}$ будем понимать число запросов, выполненных этим алгоритмом к оракулам $\mathrm{P}, \mathrm{P}^{-1}, \mathrm{E}, \mathrm{D}$ .

Определение
Функция $f(n) \colon \mathbb{N}_0 \mapsto \left[ 0, 1 \right]$ называется полиномиально мaлой (polynomially negligable), если для любого полинома $p(n)$ найдется $n_0$ , такое, что для всех $n > n_0$ выполняется $f(n) < 1 / p(n)$ :

$f(n) \text{ is polynomially negligable} \iff \exists n_0 \mid \forall n > n_0 \>\Longrightarrow\> f(n) < \frac{1}{p(n)}.$

Определение
Задачу $\mathsf{T}$ назовем трудной, если вероятность успеха любого решающего ее алгоритма, полиномиально ограниченного по времени, полиномиально мала.

Описание формальной модели

В предложенной в [EM97] модели злоумышленник в полном объеме обладает знаниями об устройстве шифра и выбранной подстановке $\pi$ . Для вскрытия системы злоумышленник использует некоторый алгоритм $\mathrm{A}$ , который может решать одну из двух задач: задачу дешифрования $\mathsf{CP}$ , или задачу построения новой пары открытый текст / шифртекст $\mathsf{EFP}$ .

Задача дешифрования ( $\mathsf{CP}$ )

Под задачей дешифрования (
$\mathsf{CP}$ , cracking problem) понимается проблема дешифрования злоумышленником некоторого закрытого текста $C_0$ . При этом всякий алгоритм $\mathrm{A}$ , используемый злоумышленником для решения задачи, может обращаться к оракулам $\mathrm{P}$ , $\mathrm{P}^{-1}$ , $\mathrm{E}$ , $\mathrm{D}'$ , где:

(ограниченный по $C_0$ ) оракул $\mathrm{D}'$ расшифровывает всякий $n$ –мерный двоичный набор (шифртекст) $C$ , кроме $C_0$ , на ключе $\underline{K}$ :

$\mathrm{D}_{\underline{K}, \pi}' \colon \mathcal{C} \equiv \mathbb{Z}_{2}^{n} \mapsto \mathcal{P} \equiv \mathbb{Z}_{2}^{n}, \quad \mathrm{D}_{\underline{K}, \pi}' \left[ C \right] = \underline{K}_1 \oplus \pi^{-1} (C \oplus \underline{K}_2) \text{ with } C \neq C_0.$

Алгоритм $\mathrm{A}$ успешно вскрывает систему, если $\operatorname{A}\left[C_0\right]} = D (C_0, \underline{K})$ .

Задача построения новой пары открытый текст / шифртекст ( $\mathsf{EFP}$ )

Под задачей построения новой пары текстов ( $\mathsf{EFP}$ , existential forgery problem) понимается проблема построения такой пары $\left\langle P, C \right\rangle$ , которая бы удовлетворяла соотношению $C = E(P, \underline{K})$ , и при этом не состояла из запроса и ответа к одному из оракулов $\mathrm{E}, \mathrm{D}$ . При этом всякий алгоритм $\mathrm{B}$ , используемый злоумышленником для решения задачи, может обращаться ко всем четырем оракулам $\mathrm{P}, \mathrm{P}^{-1}, \mathrm{E}, \mathrm{D}$ .

Успехом алгоритма $\mathrm{B}$ считается получение новой корректной пары открытого текста и шифртекста $\left\langle P, C \right\rangle$ .

Сведение задачи построения пары текст / шифртекст к задаче вскрытия ( $\mathsf{EFP} \varpropto \mathsf{CP}$ )

Теорема 1 (EFP to CP reduction)
Пусть $n \in \mathbb{N}$ , и существует алгоритм $\mathrm{A}$ , решающий задачу вскрытия $\mathrm{CP}$ за время $T(n)$ с вероятностью успеха $\xi(n)$ , тогда существует алгоритм $\mathrm{B}$ , строящий пару текстов $\left\langle P, C \right\rangle$ за то же самое время $T(n)$ с вероятностью успеха $\xi(n) / T(n)$ :

$\exists \mathrm{A} \text{ для решения } \mathsf{CP} \mid T_{\mathrm{A}} = T(n),\ p_{\mathrm{A}} = \xi(n) \>\Longrightarrow\> \exists \mathrm{B} \text{ для решения } \mathsf{EFP} \mid T_{\mathrm{B}} \leq T(n),\ p_{\mathrm{B}} = \frac{\xi(n)}{T(n)}.$

Доказательство

Зафиксируем открытый текст $P_0$ , ключ $\underline{K}$ и шифртекст $C_0 = E (P_0, \underline{K})$ , и рассмотрим ход выполнения алгоритма $\operatorname{A}\left[C_0\right]}$ .

Без ограничения общности можно полагать, что, если алгоритм $\mathrm{A}$ успешно дешифрует $C_0$ , то в некоторый критический момент времени $T' < T(n)$ выполнения этого алгоритма злоумышленник проверяет найденный открытый текст,–, кандидат $P_0$ , отправив (впервые) запрос на его шифрование к оракулу $\mathrm{E}$ и сравнив дешифруемый шифртекст $C_0$ с ответом оракула:

$\operatorname{E_K}\left[P_0\right]} \stackrel{?}{=} C_0.$

На основании алгоритма $\mathrm{A}$ построим алгоритм $\mathrm{B}$ , решающий задачу $\mathsf{EFP}$ :

Зафиксируем шифртекст $C_0 \in \mathcal{C}$ ;
Начнем выполнение алгоритма $\operatorname{A}\left[C_0\right]}$ ;
Выберем случайное $\tau$ , распределенное равномерно на отрезке $\left[1, t(n)\right]$ ;
Остановим выполнение алгоритма $\operatorname{A}\left[C_0\right]}$ после $\tau - 1$ запросов к оракулам;
Если в запросе $\tau$ алгоритм $\operatorname{A}\left[C_0\right]}$ запрашивает шифрование $P'$ , то выполнение алгоритма прекращается, и исходная пара — $\left\langle P', C_0 \right\rangle$ .

Легко видеть, что алгоритм $\mathrm{B}$ осуществляет не более $T(n)$ запросов к оракулам $\mathrm{E}, \mathrm{D}$ , при этом искомая пара $\left\langle P', C_0 \right\rangle$ будет построена только в том случае, если алгоритм дешифрования $\mathrm{A}$ успешно дешифрует текст $C_0$ (с вероятностью $p_{\mathrm{A}} = \xi(n)$ ) и $\mathrm{A}$ будет остановлен в критический момент времени $T'$ (с вероятностью $1 / T(n)$ ):

$p_{\mathrm{B}} = p_{\mathrm{A}} \cdot \frac{1}{T(n)} = \frac{\xi(n)}{T(n)},$

что и требовалось доказать.

Следствие 1.1
Пусть задача $\mathsf{EFP}$ трудна (для любого полиномиального решающего алгоритма $\mathrm{B}$ его вероятность успеха $p_{\mathrm{B}}$ полиномиально мала), тогда задача $\mathsf{CP}$ тоже трудна (для любого полиномиального решающего алгоритма $\mathrm{A}$ его вероятность успеха $p_{\mathrm{A}}$ полиномиально мала).

Следует заметить, что обратное утверждение (сводимость $\mathsf{CP} \varpropto \mathsf{EFP}$ ) не верно в общем случае: в некоторых классах криптосистем существуют открытые тексты, такие, что соответствующие им шифртексты заранее известны и не зависят от ключа (например, $P = 1$ в схеме RSA).

Стойкость системы при использовании случайной подстановки $\pi$

Основные идеи доказательства стойкости заключаются в следующем:

показать, что на любом этапе полиномиально ограниченной атаки, множество «хороших» ключей (ключей, истинность которых злоумышленник ни подтвердить, ни опровергнуть на основе имеющихся у него данных) экспоненциально велико (Лемма 1);
показать, что злоумышленник может «угадать» истинный ключ $\underline{K}$ только с полиномиально малой вероятностью (Теорема 2);
показать, что злоумышленник собрать достаточно данных для выявления истинного ключа $\underline{K}$ за полиномиальное число запросов к оракулам (Теорема 2).

Определение
Первый подключ $K_1$ ключа $K = \left\langle K_1, K_2 \right\rangle$ называется плохим относительно алгоритма $\mathrm{A}$ и выработанных им множеств $\mathsf{E}$ и $\mathsf{P}$ , если существуют $E$ –пара $\left\langle P_i, C_i \right\rangle \in \mathsf{E}$ и $P$ –пара $\left\langle M_j, \pi(M_j) \right\rangle \in \mathsf{P}$ , такие, что $P_i \oplus K_1 = M_j$ ; и хорошим в другом случае:

$K_1 \text{ is a bad key} \iff \exists \left\langle P_i, C_i \right\rangle \in \mathsf{E}, \left\langle M_j, \pi(M_j) \right\rangle \in \mathsf{P} \>\Longrightarrow\> P_i \oplus K_L = M_j.$

Другими словами, подключ $K_1$ будем считать хорошим, если на основе материала, полученного в результате выполнения алгоритма $\mathrm{A}$ невозможно выяснить, является ли $K_1$ подключом истинного ключа $\underline{K}$ . Поясним это неформальное определение следующим примером: пусть подключ $K_1$ является плохим, тогда, согласно определению плохого подключа, найдутся $E$ –пара $\left\langle P_i, C_i \right\rangle,$ где $C_i = E(P_i, \left\langle \underline{K}_1, \underline{K}_2 \right\rangle)$ , и $P$ –пара $\left\langle P_i \oplus K_1, \pi (P_i \oplus K_1) \right\rangle$ . Тогда ключ $K = \left\langle K_1, K_2 \right\rangle$ является кандидатом на роль истинного ключа $\underline{K}$ , где

$K_2 = C_i \oplus \left( \pi (P_i \oplus K_1) \right).$

Очевидно, такой ключ $K = \left\langle K_1, K_2 \right\rangle$ удовлетворяет этой $E$ –паре, ведь

$E(P_i, K) = K_2 \oplus \pi (K_1 \oplus P_i) = \big( C_i \oplus (\pi (P_i \oplus K_1))\big) \oplus \pi (K_1 \oplus P_i) = C_i.$

С помощью других собранных $E$ –пар и $P$ –пар злоумышленник имеет возможность проверить, является ли построенный таким образом ключ $K$ истинным ключом $\underline{K}$ вскрываемой системы; и принять (в качестве подключа $\underline{K}_1$ ), либо отбросить подключ $K_1$ .

Аналогичное определение можно сформулировать и для вторых подключей $K_2$ .

Определение
Второй подключ $K_2$ ключа $K = \left\langle K_1, K_2 \right\rangle$ называется плохим относительно алгоритма $\mathrm{A}$ и выработанных им множеств $\mathsf{E}$ и $\mathsf{P}$ , если существуют $E$ –пара $\left\langle P_i, C_i \right\rangle \in \mathsf{E}$ и $P$ –пара $\left\langle M_j, \pi(M_j) \right\rangle \in \mathsf{P}$ , такие, что $C_i \oplus K_2 = \pi(M_j)$ ; и хорошим в другом случае:

$K_2 \text{ — плохой} \iff \exists \left\langle P_i, C_i \right\rangle \in \mathsf{E}, \left\langle M_j, \pi(M_j) \right\rangle \in \mathsf{P} \>\Longrightarrow\> C_i \oplus K_2 = \pi(M_j).$

Определение
Ключ $K = \left\langle K_1, K_2 \right\rangle$ называется хорошим, если оба подключа $K_1$ и $K_2$ являются хорошими, и плохим в другом случае.

Утверждение 2 (True subkeys share goodness)
При секретном ключе $\underline{K} = \left\langle \underline{K}_1, \underline{K}_2 \right\rangle$ и перестановке $\pi$ подключи $\underline{K}_1$ и $\underline{K}_2$ либо оба являются хорошими, либо плохими:

$\underline{K}_1 \text{ is a good key} \iff \underline{K}_2 \text{ is a good key} \quad (\text{when } \underline{K}, \pi \text{ are fixed}).$

Лемма 1 (The fraction of bad keys)
Пусть алгоритм $\mathrm{A}$ выработал множества $\mathsf{E}, \left\vert\,{\mathsf{E}\,\right\vert = l$ и $\mathsf{P}, \left\vert\,{\mathsf{P}\,\right\vert = m$ непересекащихся $E$ –пар и $P$ –пар соответственно, тогда доля $Q$ плохих ключей в ключевом пространстве $\mathcal{K}$ не превышает $2lm / 2^n$ .

Доказательство

Согласно определению плохого подключа, некоторый подключ $K_1$ является плохим, если найдется $E$ –пара $\left\langle P_{i}, C_{i} \right\rangle \in \mathsf{E}$ и $P$ –пара $\left\langle M_{j}, \pi(M_{j})\right\rangle \in \mathsf{P}$ , такие, что

$P_{i} \oplus K_1 = M_{j}, \text{ или } K_1 = P_{i} \oplus M_{j}.$

В крайнем случае, последнее равенство может выполниться для всех наборов $i, j$ , тогда, при различных $P_{i} \mid 1 \leq i \leq l$ и $M_{j} \mid 1 \leq j \leq m$ , все $\left\vert\,\mathsf{E}\,\right\vert \cdot \left\vert\,\mathsf{P} \,\right\vert = l \cdot m$ подключей $K_1$ являются плохими.

Аналогичные рассуждения приводят к тому, что наибольшее число плохих подключей $K_2$ тоже не превышает $lm$ .

Оба подключа выбираются из $\mathbb{Z}_{2}^{n}$ , что позволяет получить верхние оценки для числа плохих ключей:

$\# \left\lbrace K \text{ is a bad key} \right\rbrace \leq lm \cdot 2^n + lm \cdot 2^n = 2 lm 2^n,$

и доли плохих ключей в ключевом пространстве $\mathcal{K} = \mathbb{Z}_2^{2n}$ :

$Q \leq \frac{2 lm 2^n}{2^{2n}} = \frac{2lm}{2^n}.$

что и требовалось доказать.

Определение
Пусть $\sigma$ — подстановка из $S_{\left\vert\,\mathcal{P}\,\right\vert}$ , а $K = \left\langle K_1, K_2 \right\rangle$ — некоторый ключ.
Будем говорить, что пара $\left\langle \sigma, K \right\rangle$ удовлетворяет (satisfies) множествам $E$ –пар $\mathsf{E}$ и $P$ –пар $\mathsf{P}$ , если выполняются следующие условия:

подстановка $\sigma$ неотличима от истинной подстановки $\pi$ на полученных множестве $P$ –пар:

$\forall \left\langle M, \pi(M) \right\rangle \in \mathsf{P} \>\Longrightarrow\> \sigma(M) = \pi(m),$

подстановка $\sigma$ неотличима от истинной подстановки $\pi$ на полученных множестве $E$ –пар:

$\forall \left\langle P, C \right\rangle \in \mathsf{E} \>\Longrightarrow\> \sigma(P \oplus K_1) = C \oplus K_2.$

Следующая лемма показывает, что все хорошие ключи являются, в некотором смысле, равными кандидатами на роль истинного ключа шифрования $\underline{K}$ .

Лемма 2 (Distribution of true key candidates)
Пусть $\mathsf{E}, \left\vert\,\mathsf{E}\,\right\vert = l$ и $\mathsf{P}, \left\vert\,\mathsf{P}\,\right\vert = m$ — множества $E$ –пар и $P$ –пар соответственно, а $\underline{K}$ — истинный ключ, тогда вероятность того, что некоторый ключ $K_{i} \in \mathcal{K}$ является секретным ключом $\underline{K}$ , одинакова для всех $i$ :

$\forall i \mid 1 \leq {i} \leq \left\vert\,{\mathcal{K}\,\right\vert \>\Longrightarrow\> \Pr{\left[\underline{K} = K_{i}\right]} = \alpha = \operatorname{const}.$

Доказательство

При условии, что ключи распределены равномерно:

$\forall K_{i} \in \mathcal{K} \>\Longrightarrow\> \Pr{\left[K_{i} = \underline{K}\right]} = \frac{1}{2^{2n}},$

и подстановка $\pi$ выбрана случайно:

$\forall \sigma_{i} \in S_{\left\vert\,\mathcal{P}\,\right\vert} \>\Longrightarrow\> \Pr{\left[\sigma_{i} = \pi\right]} = \frac{1}{2^n !},$

получаем, что искомая вероятность является условной вероятностью

$\alpha = \Pr{\left[K_{i} = \underline{K} \mid \left\langle \pi, K_{i} \right\rangle \text{ satisfies } \mathsf{E}, \mathsf{P}\right]}.$

Воспользуемся формулой Байеса:

$\Pr{\left[K_{i} = \underline{K} \mid \left\langle \pi, K_{i \right\rangle} \text{ satisfies } \mathsf{E}, \mathsf{P}\right]} = \frac { \overbrace{ \Pr{\left[K_{i} = \underline{K}\right]} }^{\operatorname{const}} \cdot \overbrace{ \Pr{\left[\left\langle \pi, K_{i \right\rangle} \text{ satisfies } \mathsf{E}, \mathsf{P} \mid K_{i} = \underline{K}\right]} }^{\beta} } { \underbrace{ \Pr{\left[\left\langle \pi, K_{i} \right\rangle \text{ satisfies } \mathsf{E}, \mathsf{P} \right]} }_{\operatorname{const}} }.$

Легко видеть, что доказательство леммы сводится к доказательству утверждения $\beta = \operatorname{const}$ .

Покажем, что для любого ключа $K_{i} = \left\langle K_{i, 1 \right\rangle, K_{i, 2}}$ множество $E$ –пар $\mathsf{E}$ можно преобразовать в эквивалентное множество $P$ –пар $\mathsf{P}'$ , ограничивающих подстановку $\pi$ , по следующему правилу:

$\forall \underbrace{\left\langle P_{i}, C_{i} \right\rangle}_{E \text{ pair}} \in \mathsf{E} \leadsto \underbrace{\left\langle P_{i} \oplus K_{i, 1}, C_{i} \oplus K_{i, 2} \right\rangle }_{P \text{ pair}} \in \mathsf{P}'.$

Очевидно, что, при фиксированной подстановке $\pi$ , если ключ $K_{i}$ удовлетворяет $P$ –паре $\left\langle P_{i} \oplus K_{i, 1}, C_{i} \oplus K_{i, 2} \right\rangle$ , то он удовлетворяет и $E$ –паре $\left\langle P_{i}, C_{i} \right\rangle$ . Заметим также, что $\left\vert\, \mathsf{E} \,\right\vert = \left\vert\,{\mathsf{P}'\,\right\vert$ , потому что указанное отображение задает биекцию $\mathsf{E} \mapsto \mathsf{P}'$ .

Так, выражение для вероятности $\beta$ принимает следующий вид:

$\beta \equiv \Pr{ \left[ \left\langle \pi, K_{i} \right\rangle \text{ satisfies } \mathsf{E}, \mathsf{P} \mid K_{i} = \underline{K} \right] } = \Pr{ \left[ \left\langle \pi, K_{i} \right\rangle \text{ satisfies } \emptyset, \mathsf{P} \cup \mathsf{P}' \mid K_{i} = \underline{K} \right] }$

Если при этом ключ $K_{i}$ является хорошим, то множества $P$ –пар $\mathsf{P}$ и $\mathsf{P}'$ не пересекаются по определению хорошего ключа:

$K_i \text{ is a good key} \>\Longrightarrow\> \mathsf{P} \cap \mathsf{P}' = \emptyset.$

В этом случае искомая вероятность $\beta$ является вероятностью того, что (выбранная случайно) подстановка $\pi$ удовлетворяет $\left\vert\,{\mathsf{E}\,\right\vert + \left\vert\,{\mathsf{P}\,\right\vert = l + m$ ограничениям. Эта вероятность не зависит от ключа $K_{i}$ и равна

$\beta = \Pr{\left[ \pi(M) = M' \mid \left\langle M, M' \right\rangle \in \mathsf{P} \cup \mathsf{P}' \right]} = \frac{\left( 2^n - (l + m) \right) !}{2^n !} = \prod_{j = 0}^{l + m - 1} \frac{1}{2^n - i}.$

Так, все вероятности в выражении для вероятности постоянны и не зависят от ключа $K_{i}$ , что и требовалось доказать.

Теорема 2 (Boundary for success probability of any $\mathrm{A}$ solving $\mathsf{EFP}$ ) Пусть подстановка $\pi$ выбрана случайно из $S_{\left\vert\,\mathcal{P}\,\right\vert}$ и ключ $\underline{K}$ выбран случайно из $\mathbb{Z}_{2}^{2n}$ , тогда для вероятности успеха алгоритма $\mathrm{A}$ , решающего задачу $\mathsf{EFP}$ , справедлива следующая верхняя оценка:

$p_{\mathrm{A}} = \mathcal{O}\!\left(\frac{lm}{2^n}\right),$

где $l$ — число запросов к оракулам $\mathrm{E}$ и $\mathrm{D}$ , а $m$ — число запросов к оракулам $\mathrm{P}$ и $\mathrm{P}^{-1}$ .

Доказательство

Допустим, существует некоторый алгоритм $\mathrm{A}$ , который решает задачу $\mathsf{EFP}$ и при этом вырабатывает множества $\mathsf{E}, \left\vert\,{\mathsf{E}\,\right\vert = l$ и $\mathsf{P}, \left\vert\,{\mathsf{P}\,\right\vert$ $E$ –пар и $P$ –пар сооветственно. Этот алгоритм может достигнуть успеха лишь в одном из двух случаев: либо истинный ключ $\underline{K}$ становится плохим на одном из шагов выполнения алгоритма, либо по истечении $l + m$ шагов алгоритм $\mathrm{A}$ просто «угадывает» корректную пару $\left\langle P, C \right\rangle$ , при условии $\underline{K} \in \mathcal{K}^{(l + m)}$ .

Обозначим через $\mathsf{E}^{(r)}$ и $\mathsf{P}^{(r)}$ множества $E$ –пар и $P$ –пар, порожденные алгоритмом $\mathrm{A}$ при первых $r - 1$ запросах:

$\mathsf{E}^{(r)} \subseteq \mathsf{E},\ \big\lvert \mathsf{E}^{(r)} \big\rvert = l^{(r)} \leq l = \left\vert\,{\mathsf{E}\,\right\vert,\quad \mathsf{P}^{(r)} \subseteq \mathsf{P},\ \big\lvert \mathsf{P}^{(r)} \big\rvert = m^{(r)} \leq m = \left\vert\,{\mathsf{P}\,\right\vert.$

Обозначим через $\mathcal{K}^{(r)}$ множество ключей, хороших относительно множеств $\mathsf{E}^{(r)}$ и $\mathsf{P}^{(r)}$ . Тогда по лемме, доказанной ранее, число таких ключей можно оценить следующим образом:

$\big\lvert \mathcal{K}^{(r)} \big\rvert \geq 2^{2n} - 2 l^{(r)} m^{(r)} 2^n \geq 2^{2n} - 2lm 2^n.$

Без ограничения общности можно предположить, что истинный ключ $\underline{K}$ принадлежит этому множеству (является хорошим). Будем считать, что алгоритм $\mathrm{A}$ успешен, если в результате следующего, $r$ –го запроса ключ $\underline{K}$ окажется плохим. Заметим, что такое определение успеха не соответствует определению, данному ранее, но является необходимым условием для последнего.

Рассмотрим все возможные типы запросов, которые могут быть отправлены алгоритмом $\mathrm{A}$ к оракулам на следующем, $r$ –м шаге, и выясним, какие из них, и с какой вероятностью, исключат ключ $\underline{K}$ из числа хороших ключей ( $\underline{K} \notin \mathcal{K}_{i + 1}$ ):

запрос к оракулу $\mathrm{E}$ :

Пусть $\left\langle P, C \right\rangle$ — сформированная в результате такого запроса $E$ –пара. Возможны два варианта:

- пара $\left\langle P, C \right\rangle \in \mathsf{E}^{(r)}$ , в таком случае выработанные алгоритмом множества не изменятся, и ключ $\underline{K}$ останется хорошим;
- пара $\left\langle P, C \right\rangle \notin \mathsf{E}^{(r)}$ , в таком случае имеют место следующие равенства:

$\mathsf{E}^{(r + 1)} = \mathsf{E}^{(r)} \cup \left\langle P, C \right\rangle; \quad \mathsf{P}^{(r + 1)} = \mathsf{P}^{(r)}.$

Подсчитаем число ключей $\Delta_{r, r+1} Q_{\mathrm{E}, K}$ , которые стали плохими в результате формирования такой пары $\left\langle P, C \right\rangle$ . Ключ $K = \left\langle K_1, K_2 \right\rangle$ является плохим, если плохим является хотя бы один из его подключей $K_1, K_2$ :

$\big\lvert \mathcal{K}^{(r)} \setminus \mathcal{K}^{(r + 1)} \big\rvert \leq \#{K_1 }$

Число $Q_{K_1}^{(r + 1)}$ плохих подключей $K_1$ (на шаге $r$ ) по определению плохого подключа равно числу различных сумм $P_i \oplus M_j$ , где индекс $i$ пробегает по всем $E$ –парам множества $\mathsf{E}^{(r + 1)}$ , а индекс $j$ — по всем $P$ –парам множества $\mathsf{P}^{(r + 1)}$ :

$Q_{K_1}^{(r + 1)} = \#\left\lbrace K_1 \text{ is a bad key} \right\rbrace = \#\left\lbrace P_i \oplus M_j \mid \left\langle P_i, C_i \right\rangle \in \mathsf{E}^{(r + 1)}, \left\langle M_j, M_j' \right\rangle \in \mathsf{P}^{(r + 1)} \right\rbrace}.$

Учитывая полученные выше равенства для $\mathsf{E}^{(r + 1)}$ и $\mathsf{P}^{(r + 1)}$ , получаем:

$Q_{K_1}^{(r + 1)} = Q_{K_1}^{(r)} + \#\left\lbrace P \oplus M_j \provided \left\langle M_j, M_j' \right\rbrace \in \mathsf{P}^{(r) \right\rangle} \leq Q_{K_1}^{(r)} + m.$

По аналогичным соображениям, число плохих подключей $K_2$ тоже не больше $Q_{K_2}^{(r)} + m$ :

$Q_{K_2}^{(r + 1)} = Q_{K_2}^{(r)} + \#\left\lbrace C \oplus M_j' \provided \left\langle M_j, M_j' \right\rbrace \in \mathsf{P}^{(r) \right\rangle} \leq Q_{K_2}^{(r)} + m.$

Тогда число $Q_K^{(r + 1)}$ плохих ключей $K$ на шаге $r$ оценивается следующим образом:

$Q_K^{(r + 1)} \leq Q_{K_1}^{(r + 1)} \cdot 2^n + 2^n \cdot Q_{K_2}^{(r + 1)} = Q_K^{(r)} + 2 m 2^n,$

и искомая разность равна:

$\Delta_{r, r+1} Q_{\mathrm{E}, K} = Q_K^{(r + 1)} - Q_K^{(r)} \leq 2 m 2^n.$

Вероятность того, что (случайно выбраный) ключ $\underline{K}$ окажется среди $\Delta_{r, r+1} Q_{\mathrm{E}, K}$ ключей, которые стали плохими (в результате запроса к оракулу $\mathrm{E}$ ), равна

$\Pr{\left[ \underline{K} \in \mathcal{K}^{(r)} \setminus \mathcal{K}^{(r + 1)} \mid \left\langle P, C \right\rangle \right]} = \frac{ \Delta_{r, r+1} Q_{\mathrm{E}, K} }{ Q_K^{(r)} } \leq \frac{2m}{2^n - 2lm} .$

запрос к оракулу $\mathrm{D$

По аналогии с запросом к оракулу $\mathrm{E}$ , вероятность того, что ключ $\underline{K}$ окажется плохим (в результате запроса к оракулу $\mathrm{D}$ ), не превышает

$\Pr{\left[ \underline{K} \in \mathcal{K}^{(r)} \setminus \mathcal{K}^{(r + 1)} \mid \left\langle P, C \right\rangle \right]} = \frac{ \Delta_{r, r+1} Q_{\mathrm{D}, K} }{ Q_K^{(r)} } \leq \frac{2m}{2^n - 2lm} .$

запрос к оракулу $\mathrm{P}$

Пусть $\left\langle M, M' \right\rangle$ — сформированная в результате такого запроса $P$ –пара. Возможны два варианта:

- пара $\left\langle M, M' \right\rangle \in \mathsf{P}^{(r)}$ , в таком случае выработанные алгоритмом множества не изменятся, и ключ $\underline{K}$ останется хорошим;
- пара $\left\langle M, M' \right\rangle \notin \mathsf{P}^{(r)}$ , в таком случае имеют место следующие равенства:

$\mathsf{E}^{(r + 1)} = \mathsf{E}^{(r)}; \quad \mathsf{P}^{(r + 1)} = \mathsf{P}^{(r)} \cup \left\langle M, M' \right\rangle.$

Подсчитаем число ключей $\Delta_{r, r+1} Q_{\mathrm{P}, K}$ , которые стали плохими в результате формирования такой пары $\left\langle M, M' \right\rangle$ .

Число $Q_{K_1}^{(r + 1)}$ плохих подключей $K_1$ (на шаге $r$ ) по определению плохого подключа равно числу различных сумм $P_i \oplus M_j$ , где индекс $i$ пробегает по всем $E$ –парам множества $\mathsf{E}^{(r + 1)}$ , а индекс $j$ — по всем $P$ –парам множества $\mathsf{P}^{(r + 1)}$ :

Учитывая равенства для $\mathsf{E}^{(r + 1)}$ и $\mathsf{P}^{(r + 1)}$ , получаем:

$Q_{K_1}^{(r + 1)} = Q_{K_1}^{(r)} + \#\left\lbrace P_i \oplus M \mid \left\langle P_i, C_i \right\rangle \in \mathsf{E}^{(r)} \right\rbrace \leq Q_{K_1}^{(r)} + l.$

По аналогичным соображениям, число плохих подключей $K_2$ тоже не больше $Q_{K_2}^{(r)} + l$ :

$Q_{K_2}^{(r + 1)} = Q_{K_2}^{(r)} + \#\left\lbrace C \oplus M_j' \mid \left\langle M_j, M_j' \right\rangle \in \mathsf{P}^{(r)} \right\rbrace \leq Q_{K_2}^{(r)} + m.$

Тогда число $Q_K^{(r + 1)}$ плохих ключей $K$ на шаге $r$ оценивается следующим образом:

$Q_K^{(r + 1)} \leq Q_{K_1}^{(r + 1)} \cdot 2^n + 2^n \cdot Q_{K_2}^{(r + 1)} = Q_K^{(r)} + 2 l 2^n,$

и искомая разность:

$\Delta_{r, r+1} Q_{\mathrm{P}, K} = Q_K^{(r + 1)} - Q_K^{(r)} \leq 2 l 2^n.$

Вероятность того, что (случайно выбраный) ключ $\underline{K}$ окажется среди $\Delta_{r, r+1} Q_{\mathrm{P}, K}$ ключей, которые стали плохими (в результате запроса к оракулу $\mathrm{P}$ ), равна

$\Pr{\left[ \underline{K} \in \mathcal{K}^{(r)} \setminus \mathcal{K}^{(r + 1)} \mid \left\langle M, M' \right\rangle \right]} = \frac{\Delta_{r, r+1} Q_{\mathrm{P}, K}}{Q_K^{(r)}} \leq \frac{2l}{2^n - 2lm}.$

запрос к оракулу $\mathrm{P^{-1}}$ .

По аналогии с запросом к оракулу $\mathrm{P}$ , вероятность того, что ключ $\underline{K}$ окажется плохим (в результате запроса к оракулу $\mathrm{P}^{-1}$ ), не превышает

$\Pr{\underline{K} \in \mathcal{K}^{(r)} \setminus \mathcal{K}^{(r + 1)} \provided \left\langle M, M' \right\rangle} = \frac{\Delta_{r, r+1} Q_{\mathrm{P}^{-1}, K}}{Q_K^{(r)}} \leq \frac{2l}{2^n - 2lm}.$

Делаем выводы:
$E$ –пара $\left\langle P, C \right\rangle$ , выработанная на шаге $r$ , приведет к тому, что ключ $\underline{K}$ окажется плохим, с вероятностью, не большей $2m / (2^n - 2lm)$ , тогда ключ $\underline{K}$ станет плохим в результате хотя бы одного из $l$ таких запросов ( $l = \left\vert\,\mathsf{E}\,\right\vert$ ), не больше $2lm / (2^n - 2lm)$ .

Аналогично, ключ $\underline{K}$ станет плохим в результате хотя бы одного из $m$ запросов к оракулам $\mathrm{P},$ $\mathrm{P}^{-1}$ , так же не больше $2lm / (2^n - 2lm)$ . Тогда получаем верхнюю оценку вероятности того, что истинный ключ $\underline{K}$ вообще станет плохим в процессе выполнения алгоритма $\mathrm{A}$ :

$\Pr{\underline{K} \in \mathcal{K} \setminus \mathcal{K}^{(l + m)}} \leq \frac{4lm}{2^n - 2lm}.$

В другом случае алгоритм $\mathrm{A}$ «угадывает» корректную $E$ –пару $\left\langle P, C \right\rangle$ :

$\pi(P \oplus \underline{K}_1) \oplus \underline{K}_2 = C$

по истечении $l + m$ запросов, при этом ключ $\underline{K}$ — хороший относительно множеств $\mathsf{E} \cup \left\langle P, C \right\rangle$ и $\mathsf{P}$ . По определению хорошего ключа, не существует среди всех $P$ –пар множества $\mathsf{P}$ ни одной такой пары $\left\langle M, M' \right\rangle$ , что $P \oplus \underline{K}_1 = M$ либо $C \oplus \underline{K}_2 = M'$ .

Заметим, что значение подстановки $\pi$ в точке $P \oplus \underline{K}_1$ не ограничено ни одной $P$ –парой множества $\mathsf{P}$ в силу того, что ключ $\underline{K}$ хороший и ни одной $E$ –парой в силу того, что «угаданная» пара $\left\langle P, C \right\rangle$ — новая. Так, $\pi(P \oplus \underline{K}_1)$ может принимать любое из $2^n - (m + l)$ «значений», и искомая вероятность

$\Pr{\left[ \pi(P \oplus \underline{K}_1) = C \oplus \underline{K}_2 \right]} = \frac{1}{2^n - (m + l)} = \mathcal{O}\!\left(\frac{lm}{2^n}\right).$

Тогда вероятность успеха $p_{\mathrm{A}}$ алгоритма $\mathrm{A}$ :

$p_{\mathrm{A}} \leq \frac{4lm}{2^n - 2lm} + \frac{1}{2^n - (m + l)} = \bigo{\frac{lm}{2^n}},$

что и требовалось доказать.

Следствие 2.1
Пусть подстановка $\pi$ выбрана случайно из $S_{\left\vert\,\mathcal{P}\,\right\vert}$ , тогда вероятность успеха любого алгоритма $\mathrm{A}$ , решающего задачу $\mathsf{EFP}$ и полиномиально ограниченного по числу запросов к оракулам $\mathrm{P},$ $\mathrm{P}^{-1},$ $\mathrm{E},$ $\mathrm{D},$ полиномиальна мала.

Стойкость системы при использовании псевдослучайной подстановки $\pi$

Предложенный в [EM97] шифр сохраняет показанное свойство криптостойкости и в том случае, если подстановка $\pi$ выбрана псевдослучайно.

Для доказательства этого утверждения достаточно пояснить понятие псевдослучайной подстановки.

Определение
Пусть $\sigma$ — случайная подстановка, а $\delta$ — некоторая подстановка, выбранные из $S_{\left\vert\,\mathcal{P}\,\right\vert}$ по некоторому неравномерному закону распределения, а $\mathrm{P}_{\sigma}$ и $\mathrm{P}_{\delta}$ — реализующие их оракулы. Будем говорить, что подстановка $\delta$ псевдослучайна, если не существует полиномиального ограниченного по количеству запросов алгоритма, различающего оракулов $\mathrm{P}_{\sigma}$ и $\mathrm{P}_{\delta}$ .

Другими словами, в представленной модели вычисления с оракулами, псевдослучайная подстановка неотличима от случайной. Поэтому имеет место следующая теорема.

Теорема 3
Пусть подстановка $\pi$ выбрана псевдослучайно из $S_{\left\vert\,{\mathcal{P}\,\right\vert}$ , тогда вероятность успеха любого алгоритма $\mathrm{A}$ , решающего задачу $\mathsf{EFP}$ и полиномиально ограниченного по числу запросов к оракулам $\mathrm{P},$ $\mathrm{P}^{-1},$ $\mathrm{E},$ $\mathrm{D},$ полиномиальна мала.

В продолжение

Да, есть еще порох в пороховницах. Если на Хабре найдутся заинтересованные, то в следующей части могу рассмотреть модификации этой классической схемы, и различные криптографические атаки на нее (которые, кстати, показывают, что полученная оценка снизу точна, и не может быть улучшена).

Список литературы

Для тех, кто очень заинтересовался:

Eli Biham, Yaniv Carmeli, Itai Dinur, Orr Dunkelman, Nathan Keller, and Adi Shamir. Cryptanalysis of iterated Even-Mansour schemes with two keys. IACR Cryptology ePrint Archive, 2013:674, 2013.
Andrey Bogdanov, Lars R Knudsen, Gregor Leander, Francois-Xavier Standaert, John Steinberger, and Elmar Tischhauser. Key-alternating ciphers in a provable setting: Encryption using a small number of public permutations. In Advances in Cryptology–EUROCRYPT 2012, pages 45–62. Springer, 2012.
Alex Biryukov and David Wagner. Advanced slide attacks. In Advances in Cryptology—EUROCRYPT 2000, pages 589–606. Springer, 2000.
Shan Chen, Rodolphe Lampe, Jooyoung Lee, Yannick Seurin, and John Steinberger. Minimizing the two-round Even-Mansour cipher. In Advances in Cryptology–CRYPTO 2014, pages 39–56. Springer, 2014.
Joan Daemen. Limitations of the Even-Mansour construction. In Advances in Cryptology—ASIACRYPT’91, pages 495–498. Springer, 1993.
Itai Dinur, Orr Dunkelman, Nathan Keller, and Adi Shamir. Key recovery attacks on 3-round Even-Mansour, 8-step LED-128, and full AES2. In Advances in Cryptology-ASIACRYPT 2013, pages 337–356. Springer, 2013.
Orr Dunkelman, Nathan Keller, and Adi Shamir. Minimalism in cryptography: The Even-Mansour scheme revisited. In Advances in Cryptology–EUROCRYPT 2012, pages 336–354. Springer, 2012.
[EM97] Shimon Even and Yishay Mansour. A construction of a cipher from a single pseudorandom permutation. Journal of Cryptology, 10(3):151– 161, 1997.
Shoni Gilboa and Shay Gueron. Balanced permutations even-mansour ciphers. arXiv preprint arXiv:1409.0421, 2014.
Philip Hawkes and Luke O’Connor. Xor and non-xor differential probabilities. In Advances in Cryptology—EUROCRYPT’99, pages 272–285. Springer, 1999.
Nicky Mouha and Atul Luykx. Multi-key security: The Even-Mansour construction revisited. Technical report, Cryptology ePrint Archive, Report 2015/101, 2015.
Ivica Nikolic, Lei Wang, and Shuang Wu. Cryptanalysis of round-reduced LED. In Shiho Moriai, editor, Fast Software Encryption, volume 8424 of Lecture Notes in Computer Science, pages 112–129. Springer Berlin Heidelberg, 2014.

P.S. Часть этой публикации была сверстана в TeX, при верстке на Хабре могли появиться косяки, в основном в формулах. Если заметите — обращайтесь, исправлю.

EDIT 1. Исправил имена ученых, спасибо alexyr.

Теги:

Хабы:

Минимализм в криптографии, или схема Even–Mansour

Лирическое отступление

Множества, наборы

Начертания

Обозначения

Определения

Классическая схема Even–Mansour

Описание

О минимальности схемы

О стойкости схемы

Предположения стойкости, определения

Описание формальной модели

Задача дешифрования ( $\mathsf{CP}$ )

Задача построения новой пары открытый текст / шифртекст ( $\mathsf{EFP}$ )

Сведение задачи построения пары текст / шифртекст к задаче вскрытия ( $\mathsf{EFP} \varpropto \mathsf{CP}$ )

Стойкость системы при использовании случайной подстановки $\pi$

Стойкость системы при использовании псевдослучайной подстановки $\pi$

В продолжение

Список литературы

Публикации

Истории

Работа

Ближайшие события

Минимализм в криптографии, или схема Even–Mansour

Лирическое отступление

Множества, наборы

Начертания

Обозначения

Определения

Классическая схема Even–Mansour

Описание

О минимальности схемы

О стойкости схемы

Предположения стойкости, определения

Описание формальной модели

Задача дешифрования ()

Задача построения новой пары открытый текст / шифртекст ()

Сведение задачи построения пары текст / шифртекст к задаче вскрытия ()

Стойкость системы при использовании случайной подстановки

Стойкость системы при использовании псевдослучайной подстановки

В продолжение

Список литературы

Задача дешифрования ( $\mathsf{CP}$ )

Задача построения новой пары открытый текст / шифртекст ( $\mathsf{EFP}$ )

Сведение задачи построения пары текст / шифртекст к задаче вскрытия ( $\mathsf{EFP} \varpropto \mathsf{CP}$ )

Стойкость системы при использовании случайной подстановки $\pi$

Стойкость системы при использовании псевдослучайной подстановки $\pi$