Привет сообществу!
Я Юрий Кашницкий, раньше делал здесь обзор некоторых MOOC по компьютерным наукам и искал «выбросы» среди моделей Playboy.
Сейчас я преподаю Python и машинное обучение на факультете компьютерных наук НИУ ВШЭ и в онлайн-курсе сообщества по анализу данных MLClass, а также машинное обучение и анализ больших данных в школе данных одного из российских телеком-операторов.
Почему бы воскресным вечером не поделиться с сообществом материалами по Python и обзором репозиториев по машинному обучению… В первой части будет описание репозитория GitHub с тетрадками IPython по программированию на языке Python. Во второй — пример материала курса «Машинное обучение с помощью Python». В третьей части покажу один из трюков, применяемый участниками соревнований Kaggle, конкретно, Станиславом Семеновым (4 место в текущем мировом рейтинге Kaggle). Наконец, сделаю обзор попавшихся мне классных репозиториев GitHub по программированию, анализу данных и машинному обучению на Python.
Часть 1. Курс программирования на языке Python в виде тетрадок IPython
Курс состоит из 5 уроков: обзор средств разработки, введение в язык Python, 2 урока про структуры данных (Python и не только) и некоторые алгоритмы и один урок про функции и рекурсию. Да, не затронута тема ООП и кучи всего полезного, но работа над курсом идет, репозиторий будет обновляться.
Цели данного курса:
- Познакомить с основами языка Python
- Познакомить с основными структурами данных
- Дать навыки, необходимые для разработки простых алгоритмов
Тетрадки IPython выбраны в качестве основного средства подачи материала из-за того, что в них можно совмещать текст, картинки, формулы и код. В качестве демонстрации в репозитории приведена тетрадка про деревья решений и их реализацию в библиотеке машинного обучения Scikit-learn. В материалах первого урока описано, как собственно этими тетрадками пользоваться.

Вот ссылка на репозиторий GitHub с тетрадками IPython. Ветвитесь и размножайтесь, можно использовать в любых целях, кроме коммерческих, со ссылкой на автора. Если хотите подключиться к проекту GitHub — пишите. Можно сообщать и о багах в материалах.
Часть 2. Пример материала по курсу «Машинное обучение с помощью Python". Деревья решений
Курс «Машинное обучение с помощью Python" состоит из 6 уроков и около 35 тетрадок IPython про основы машинного обучения с библиотекой Scikit-learn, использование библиотек NumPy, SciPy, Pandas, с примерами решения реальных задач Kaggle и разборов практик, используемых победителями соревнований Kaggle — стекинг, блендинг, ансамбли алгоритмов. Подробная программа здесь. В качестве примера подачи материала рассмотрим одну из первых тем — деревья решений.
Что такое дерево решений
Начнем обзор методов классификации, конечно же, с самого популярного — дерева решений.
Деревья решений используются в повседневной жизни в самых разных областях человеческой деятельности, порой и очень далеких от машинного обучения. Деревом решений можно назвать наглядную инструкцию, что делать в какой ситуации. Приведем пример из области консультирования научных сотрудников института. Высшая Школа Экономики выпускает инфо-схемы, облегчающие жизнь своим сотрудникам. Вот фрагмент инструкции по публикации научной статьи на портале института.
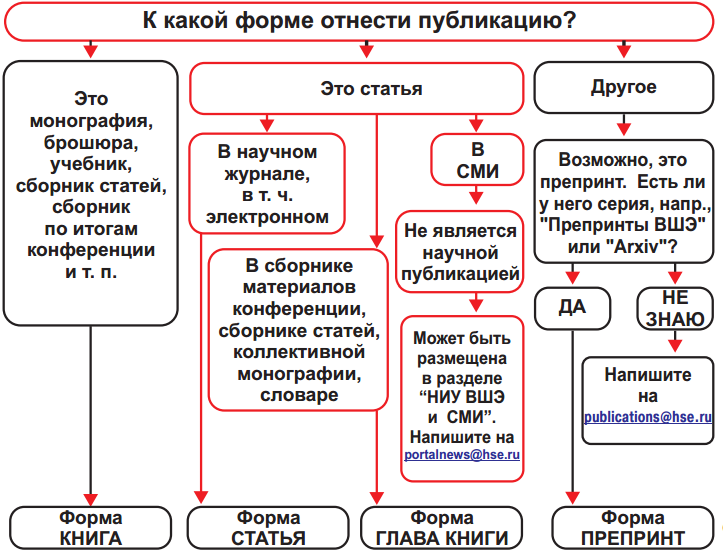
В терминах машинного обучения можно сказать, что это элементарный классификатор, который определяет форму публикации на портале (книга, статья, глава книги, препринт, публикация в «НИУ ВШЭ и СМИ») по нескольким признакам — типу публикации (монография, брошюра, статья и т.д.), типу издания, где опубликована статья (научный журнал, сборник трудов и т.д.) и остальным.
Зачастую дерево решений служит обобщением опыта экспертов, средством передачи знаний будущим сотрудникам или моделью бизнес-процесса компании. Например, до внедрения масштабируемых алгоритмов машинного обучения в банковской сфере задача кредитного скоринга решалась экспертами. Решение о выдаче кредита заемщику принималось на основе некоторых интуитивно (или по опыту) выведенных правил, которые можно представить в виде дерева решений.
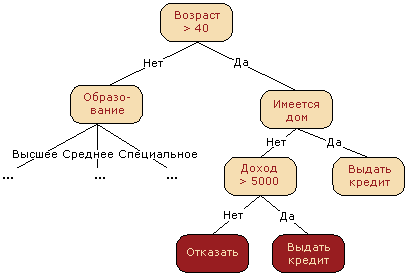
В этом случае можно сказать, что решается задача бинарной классификации (целевой класс имеет два значения — «Выдать кредит» и «Отказать») по признакам «Возраст», «Наличие дома», «Доход» и «Образование».
Дерево решений как алгоритм машинного обучения по сути — то же самое, объединение логических правил вида «Значение признака a меньше x И Значение признака b меньше y… => Класс 1» в структуру данных «Дерево». Огромное преимущество деревьев решений в том, что они легко интерпретируемы, понятны человеку. Например, по схеме на рисунке 2 можно объяснить заемщику, почему ему было отказано в кредите. Например, потому что у него нет дома и доход меньше 5000. Как мы увидим дальше, многие другие, хоть и более точные, модели не обладают этим свойством и могут рассматриваться скорее как «черный ящик», в который загрузили данные и получили ответ. В связи с этой «понятностью» деревьев решений и их сходством с моделью принятия решений человеком (можно легко объяснять боссу свою модель), деревья решений получили огромную популярность, а один из представителей этой группы методов классификации, С4.5, рассматривается первым в списке 10 лучших алгоритмов интеллектуального анализа данных (Top 10 algorithms in data mining, 2007).
Как строить дерево решений
В примере с кредитным скорингом мы видели, что решение о выдаче кредита принималось на основе возраста, наличия недвижимости, дохода и других. Но какой признак выбрать первым? Для этого рассмотрим пример попроще, где все признаки бинарные.
Здесь можно вспомнить игру «20 вопросов», которая часто упоминается во введении в деревья решений. Наверняка каждый в нее играл. Один человек загадывает знаменитость, а второй пытается отгадать, задавая только вопросы, на которые можно ответить «Да» или «Нет» (опустим варианты «не знаю» и «не могу сказать»). Какой вопрос отгадывающий задаст первым делом? Конечно такой, который сильнее всего уменьшит количество оставшихся вариантов. К примеру, вопрос «Это Анджелина Джоли?» в случае отрицательного ответа оставит более 6 миллиардов вариантов для дальнейшего перебора (конечно, поменьше, не каждый человек — знаменитость, но все равно немало), а вот вопрос «Это женщина?» отсечет уже около половины знаменитостей. То есть, признак «пол» намного лучше разделяет выборку людей, чем признак «это Анджелина Джоли», «национальность-испанец» или «любит футбол». Это интуитивно соответствует понятию прироста информации, основанного на энтропии.
Энтропия
Энтропия Шеннона определяется как
где N — число возможный реализаций, p_i (уж простите, не стал возиться с интеграцией Хабра с TeX, давно пора MathJax развернуть) — вероятности этих реализаций. Это очень важное понятие, используемое в физике, теории информации и других областях. Опуская предпосылки введения (комбинаторные и теоретико-информационные) этого понятия, отметим, что, интуитивно, энтропия соответствует степени хаоса в системе. Чем выше энтропия, тем менее упорядочена система и наоборот. Это поможет там формализовать «эффективное разделение выборки», про которое мы говорили в контексте игры «20 вопросов».
Пример
Рассмотрим игрушечный пример, в котором будем предсказывать цвет шарика по его координате. Конечно, ничего общего с жизнью это не имеет, но позволяет показать, как энтропия используется для построения дерева решений. Картинки взяты из этой статьи.

Здесь 9 синих шариков и 11 желтых. Если мы наудачу вытащили шарик, то он с вероятностью p1=9/20 будет синим и с вероятностью p2 = 11/20 — желтым. Значит, энтропия состояния S0 = -9/20 log(9/20)-11/20 log(11/20) =~ 1.
Само это значение пока ни о чем нам не говорит.
Теперь посмотрим, как изменится энтропия, если разбить шарики на две группы — с координатой меньше либо равной 12 и больше 12.
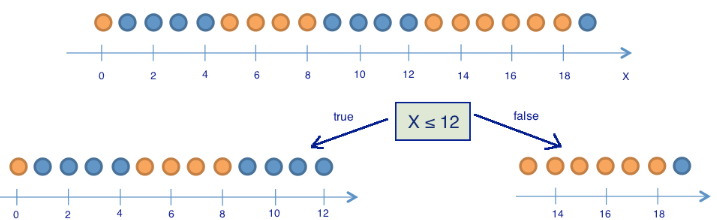
В левой группе оказалось 13 шаров, из которых 8 синих и 5 желтых. Энтропия этой группы равна S1 = -5/13 log(5/13) -8/13 log(8/13) =~ 0.96. В правой группе оказалось 7 шаров, из которых 1 синий и 6 желтых. Энтропия правой группы равна S2 = — 1/7 log(1/7) — 6/7 log(6/7) =~ 0.6. Как видим, энтропия уменьшилась в обеих группах по сравнению с начальным состоянием, хоть в левой и не сильно. Поскольку энтропия — по сути степень хаоса (или неопределенности) в системе, уменьшение энтропии называют приростом информации. Формально прирост информации (information gain, IG) при разделении выборки по признаку Q (в нашем примере это признак «x <=12») определяется как
где q — число групп после разбиения, N_i — число элементов выборки, у которых признак Q имеет i-ое значение. В нашем случае после разделения получилось две группы (q = 2) — одна из 13 элементов (N1 = 13), вторая — из 7 (N2 = 7). Прирост информации получился IG(«x <= 12») = S0 — 13/20 S1 — 7/20 S2 =~ 0.16.
Получается, разделив шарики на две группы по признаку «координата меньше либо равна 12», мы уже получили более упорядоченную систему, чем в начале. Продолжим деление шариков на группы до тех пор, пока в каждой группе шарики не будут одного цвета.
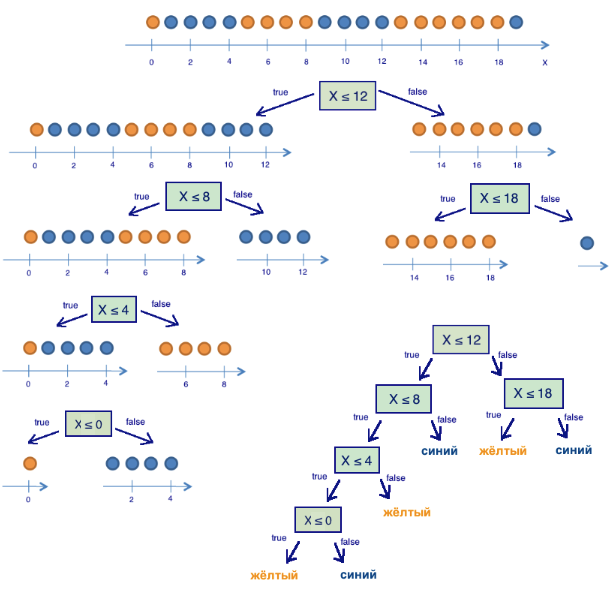
Для правой группы потребовалось всего одно дополнительное разбиение по признаку «координата меньше, либо равна 18» с приростом информации, для левой — еще три. Очевидно, энтропия группы с шариками одного цвета равно 0 (log(1)=0), что соответствует представлению, что группа шариков одного цвета — упорядоченная. В итоге построили дерево решений, предсказывающее цвет шарика по его координате. Отметим, что такое дерево решений может плохо работать для новых объектов (определения цвета новых шариков), поскольку оно идеально подстроилось под обучающую выборку (изначальные 20 шариков). Для классификации новых шариков лучше подойдет дерево с меньшим числом «вопросов», или разделений, пусть даже оно и не идеально разбивает по цветам обучающую выборку. Эту проблему, переобучение, мы еще рассмотрим далее.
Алгоритм построения дерева
Можно убедиться в том, что построенное в предыдущем примере дерево является в некотором смысле оптимальным — потребовалось только 5 «вопросов» (условий на признак x), чтобы «подогнать» дерево решений под обучающую выборку, то есть чтобы дерево правильно классифицировало любой обучающий объект. При других условиях разделения выборки дерево получится глубже.
В основе популярных алгоритмов построения дерева решений, таких как ID3 и C4.5, лежит принцип жадной максимизации прироста информации — на каждом шаге выбирается тот признак, при разделении по которому прирост информации оказывается наибольшим. Дальше процедура повторяется рекурсивно, пока энтропия не окажется равной нулю или какой-то малой величине (если дерево не подгоняется идеально под обучающую выборку во избежание переобучения). В разных алгоритмах применяются разные эвристики для «ранней остановки» или «отсечения», чтобы избежать построения переобученного дерева.
Пример
Рассмотрим пример применения дерева решений из библиотеки Scikit-learn для синтетических данных.
%pylab inline
import numpy as np
import pylab as plt
plt.rcParams['figure.figsize'] = (10.0, 8.0)
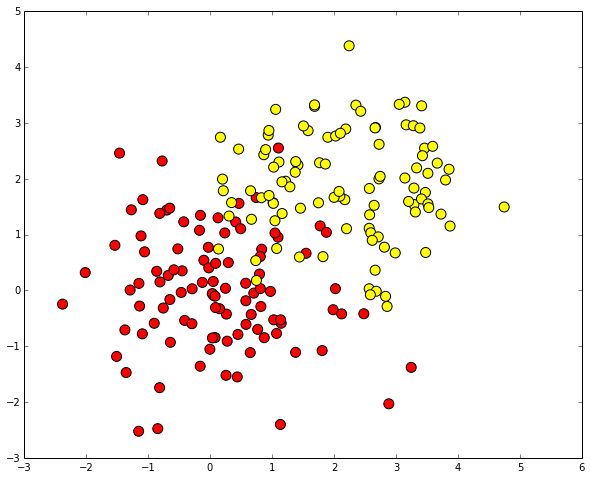
Сгенерируем данные. Два класса будут сгенерированы из двух нормальных распределений с разными средними.
# первый класс
train_data = np.random.normal(size=(100, 2))
train_labels = np.zeros(100)
# добавляем второй класс
train_data = np.r_[train_data, np.random.normal(size=(100, 2), loc=2)]
train_labels = np.r_[train_labels, np.ones(100)]
Напишем вспомогательную функцию, которая будет возвращать решетку для дальнейшей красивой визуализации
def get_grid(data):
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
return np.meshgrid(np.arange(x_min, x_max, 0.01),
np.arange(y_min, y_max, 0.01))
Отобразим данные
plt.scatter(train_data[:, 0], train_data[:, 1], c=train_labels, s=100, cmap='autumn')
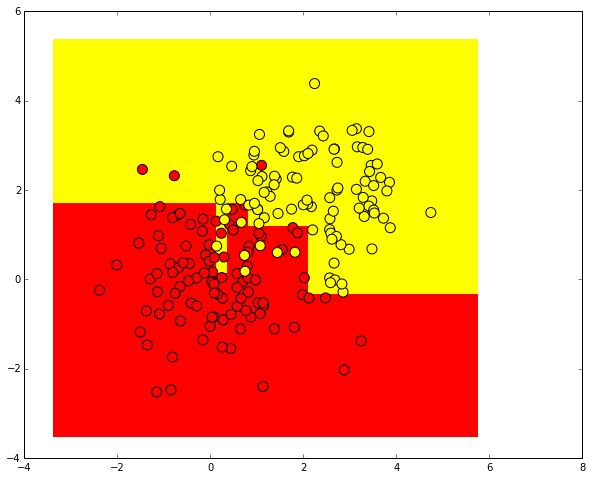
Попробуем разделить эти два класса, обучив дерево решений. Визуализируем полученную границу разделения классов.
from sklearn.tree import DecisionTreeClassifier
# параметр min_samples_leaf указывает, при каком минимальном количестве
# элементов в узле он будет дальше разделяться
clf = DecisionTreeClassifier(min_samples_leaf=5)
clf.fit(train_data, train_labels)
xx, yy = get_grid(train_data)
predicted = clf.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.pcolormesh(xx, yy, predicted, cmap='autumn')
plt.scatter(train_data[:, 0], train_data[:, 1], c=train_labels, s=100, cmap='autumn')
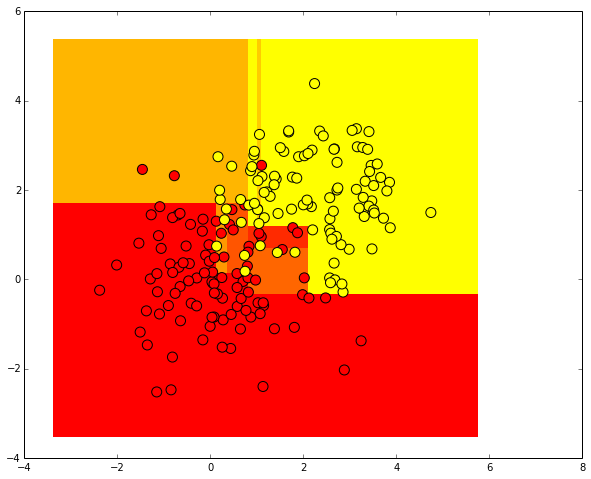
Проведем ту же процедуру, но теперь предскажем вещественные вероятности принадлежности первому классу.
Строго говоря, это не вероятности, а нормированные числа объектов разных классов из одного листа дерева.
Например, если в каком-то листе оказалось 5 положительных объектов (с меткой 1) и 2 отрицательных (с меткой 0),
то вместо того, чтобы предсказывать метку 1 для всех объектов, которые попадут на этот лист, будет предсказываться
величина 5/7.
predicted_proba = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1].reshape(xx.shape)
plt.pcolormesh(xx, yy, predicted_proba, cmap='autumn')
plt.scatter(train_data[:, 0], train_data[:, 1], c=train_labels, s=100, cmap='autumn')
Сгенерируем случайно распределенные тестовые данные.
test_data = np.random.normal(size=(100, 2), loc = 1)
predicted = clf.predict(test_data)
Отобразим их. Поскольку метки тестовых объектов неизвестны, нарисуем их серыми.
plt.scatter(test_data[:, 0], test_data[:, 1], c="gray", s=100)

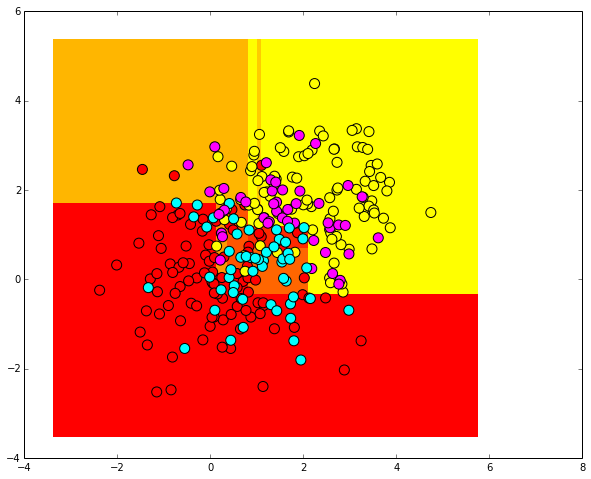
Посмотрим, как дерево решений классифицировало тестовые примеры. Для контраста используем другую цветовую гамму.
plt.pcolormesh(xx, yy, predicted_proba, cmap='autumn')
plt.scatter(train_data[:, 0], train_data[:, 1], c=train_labels, s=100, cmap='autumn')
plt.scatter(test_data[:, 0], test_data[:, 1], c=predicted, s=100, cmap='cool')
Плюсы и минусы подхода
Здесь мы познакомились с самым простым и интуитивно понятным методом классификации, деревом решений, и посмотрели, как он используется в библиотеке Scikit-learn в задаче классификации. Пока мы не обсуждали, как оценивать качество классификации и как бороться с переобучением деревьев решений. Отметим плюсы и минусы данного подхода.
Плюсы:
- Порождение четких правил классификации, понятных человеку, например, «если возраст < 25 и интерес к мотоциклам, отказать в кредите»
- Деревья решений могут легко визуализироваться
- Относительно быстрые процессы обучения и классификации
- Малое число параметров модели
- Поддержка и числовых, и категориальных признаков
Минусы:
- Разделяющая граница, построенная деревом решений, имеет свои ограничения (состоит из гиперкубов), и на практике дерево решений по качеству классификации уступает некоторым другим методам
- Необходимость отсекать ветви дерева (pruning) или устанавливать минимальное число элементов в листьях дерева или максимальную глубину дерева для борьбы с переобучением. Впрочем, переобучение — проблема всех методов машинного обучения
- Нестабильность. Небольшие изменения в данных могут существенно изменять построенное дерево решений. С этой проблемой борются с помощью ансамблей деревьев решений (рассмотрим далее)
- Проблема поиска оптимального дерева решений NP-полна, поэтому на практике используются эвристики типа жадного поиска признака с максимальным приростом информации, которые не гарантируют нахождения глобально оптимального дерева
- Сложно поддерживаются пропуски в данных. Friedman оценил, что на поддержку пропусков в данных ушло 50% кода CART.
Часть 3. Пример одного из трюков, которым мы обучаем
Рассмотрим подробней один из трюков, реально применяемых многими участниками соревнований Kaggle, в данном случае Станиславом Семеновым (4 место в текущем мировом рейтинге Kaggle на момент написания) в решении задачи «Greek Media Monitoring Multilabel Classification (WISE 2014)». Задача заключалась в классификации статей на темы. Организаторы соревнований поделились обучающей выборкой из около 65 тысяч статей, представленных с помощью моделей мешка слов и TF-IDF в виде векторов длины ~ 300 тысяч. Для каждого документа было указано, к каким темам его можно отнести (от одной темы до тринадцати разных, в среднем одна-две). Надо было предсказать, к каким темам относятся ~ 35 тысяч статей из тестовой выборки.
Разобьем обучающую выборку на проверочную (validation) и оставленную (holdout) части в пропорции 80:20. Проверочную выборку разобьем еще раз на две части. На одной обучим линейную машину опорных векторов (LinearSVC в Scikit-learn), с помощью второй будем подбирать параметр C, так чтобы максимизировать меру качества классификации F1 – целевую в данном соревновании. Holdout-выборка остается на самый конец, на ней модель проверяется перед отправкой решения. Это частая практика, позволяющая бороться с переобучением в процессе кросс-валидации.
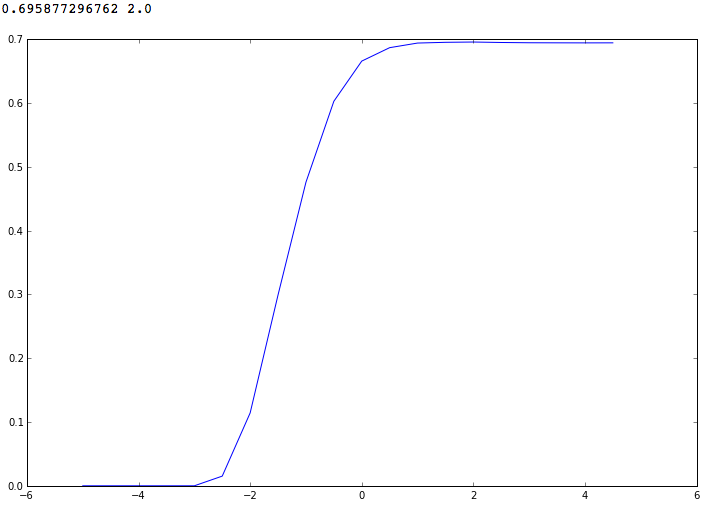
При переборе параметра в диапазоне от 10^-5 до 10^5 получим такую картину. Максимальное значение F1-меры получается при C = 100 (10^2) и равно ~ 0.6958.
Переберем параметры в более узком диапазоне – от 10^0 до 10^4. Видим, что F1 не стремится асимптотически к 0.7 при увеличении параметра C, как может показаться, а имеет локальный максимум при С = 10^1.75
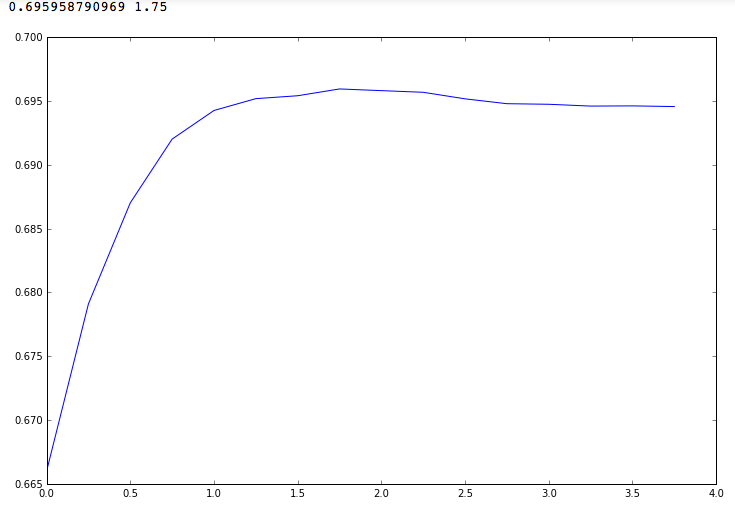
Если отправить решение, полученное на тестовой выборке с помощью LinearSVC с параметром C = 10^1.75, F1-метрика получается равной 0.61, что довольно далеко от лучших посылок.
Но подумаем над тем, как SVM классифицирует объекты в самом простом случае бинарной классификации. В данном случае, относится ли документ к какой-то теме или нет. Для каждого объекта считается расстояние от него до построенной разделяющей гиперплоскости.
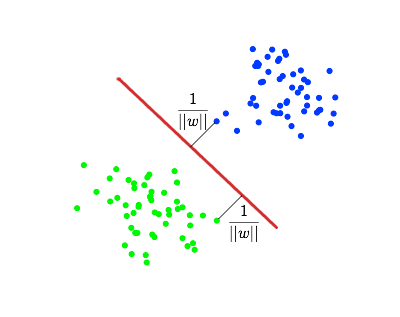
Если это расстояние положительно, объект относится к одному классу, в противном случае – к другому. Получается, граничное значение расстояния до разделяющей гиперплоскости равно 0. Но кто сказал, что это значение оптимально для классификации? Ведь в более сложном случае линейной неразделимости картинка может быть не столь простой, и построенная «разделяющая» гиперплоскость будет уже не абсолютно безошибочно разделять классы. В таком случае оптимальный (для максимизации F1-меры классификации) порог по расстоянию до гиперплоскости может отличаться от 0.
В Scikit-learn расстояние от объектов до построенной алгоритмом LinearSVC границы можно получить с помощью метода decision_function класса LinearSVC.
Посмотрим, как качество классификации (F1) будет изменяться, если менять порог расстояния от объекта до разделяющей гиперплоскости. Например, в случае порога, равного 0.1, объекты, отстоящие от гиперплоскости в одну сторону на расстояние больше 0.1, будут классифицироваться положительно, остальные – отрицательно.
При изменении порога от -2 до 2, обучении LinearSVC на одной части проверочной выборки (80%) и отслеживании F1-меры на другой части (20%) получаем такую картину.

Оказывается, для максимизации F1-меры лучше использовать порог отсечения по расстоянию до гиперплоскости равный -0.5.
В таком случае F1-мера на проверочной выборке достигает 0.763, а если обучить алгоритм на всей обучающей выборке и для классификации на тестовой использовать порог -0.5, можно достичь на публичной выборке соревнования F1 = 0.73, что сразу «поднимает» в топ 5% в рейтинге данного соревнования Kaggle (на момент написания).
Часть 4. Некоторые полезные репозитории GitHub по программированию и машинному обучению
Вот далеко не исчерпывающий список классных репозиториев GitHub по программированию, анализу данных и машинному обучению на языке Python. Почти все из них — наборы тетрадок IPython. Некоторые материалы в моем курсе, описанном выше, — перевод этих.
- Курс программирования на языке Python, основа сайта introtopython.org.
- «Data science IPython notebooks» — множество качественных тетрадок по основным библиотекам Python для анализа данных — NumPy, SciPy, Pandas, Matplotlib, Scikit-learn. Краткие обзоры Apache Spark и соревнования Kaggle «Titanic: Machine Learning from Disaster».
- Гарвардский курс анализа данных
- «Interactive coding challenges» — подборка основных задач на структуры данных, графы, сортировку, рекурсию и не только. Для многих задач приведены решения и поясняющий материал с картинками.
- Репозиторий Оливье Гризеля (одного из авторов библиотеки Scikit-learn) с обучающими тетрадками IPython. Еще один.
- Тьюториал по Scikit-learn, также от авторов
- Разбор задач курса Andrew Ng «Machine learning» на языке Python
- Материалы в дополнение к книге «Mining the Social Web (2nd Edition)» (Matthew A. Russell, издательство O'Reilly Media)
- Тьюториал по использованию ансамблей для решения задач Kaggle.
- Библиотека XGBoost, которая используется большинством победителей соревнований Kaggle. Там же можно познакомиться с их историями успеха. XGBoost хорош по качеству прогнозирования, эффективно реализован, хорошо параллелится.
- Подборка данных FiveThirtyEight. Просто куча интересных наборов данных.
- Прогнозирование результатов выборов в США. Хороший пример анализа данных с Pandas
Надеюсь, эти материалы помогут вам в изучении/преподавании Python и анализа данных.
Список классных репозиториев с тетрадками IPython (да и просто с кодом на Python), конечно, можно продолжать. Например, в комментариях.








