Автор: Komar aka Michał Trybus; Англо-русский перевод: firerock
Оригинал: blog.komar.be/how-to-make-a-keyboard-the-matrix
Это — первый пост из серии, посвящённой клавиатурам; надеюсь, он не будет последним. Хочется, чтобы в итоге получился курс по изготовлению клавиатуры с нуля. Сегодня я расскажу о цифровом вводе-выводе и о клавиатурных матрицах. Вооружитесь элементарными школьными знаниями из области электроники — и поехали.
И как же мы собираемся делать матрицу? А самое главное — зачем она вообще нужна? Ну, виной тому, в основном, физические ограничения микроконтроллеров, на базе которых строятся клавиатуры. Дело в том, что с увеличением количества выводов у микроконтроллеров и программируемых логических микросхем растёт и их размер, что, в свою очередь, влечёт за собой рост энергопотребления, возможностей, но главное — цены. В итоге, вы можете выбрать либо дешёвый чип с небольшой производительностью (которая вас вполне устраивает), но с малым количеством входов и выходов, либо более мощную микросхему, производительность которой, однако, сильно превышает ваши требования. Но только этот мощный чип будет обладать достаточным количеством выводов, чтобы подключить каждую кнопку клавиатуры.
За десятилетия в электронике сложилась практика при помощи различных ухищрений искусственно расширять встроенные коммуникационные возможности процессоров и контроллеров. Одним из таких способов, который хорошо подходит для механических контактов (кнопок), и является создание матрицы. Чтобы понять, как она работает, требуются некоторые базовые знания. Прежде, чем мы продолжим, пожалуйста, освежите в памяти закон Ома.
Чтобы разобраться, как работает цифровая электроника, надо усвоить два базовых принципа.
Принцип первый гласит, что процесс коммуникации внутри схемы — это не передача или получение чего-то там. Чтобы обеспечить коммуникацию между двумя устройствами, вы просто соединяете между собой их выводы электропроводящим материалом. После этого предполагается, что состояние материала (напряжение и ток) на обоих его концах будет одинаковым. В реальности это, конечно, не так, но для медленных коммуникаций и коротких проводников наше предположение работает отлично. Выходит, что посылка и получение информации на самом деле является её совместным использованием.
Со стороны передатчика вы просто изменяете электрическое состояние проводника (запуская в него постоянный ток, изменяя его потенциал), рассчитывая на то, что приёмник сможет определить это изменение и правильно его понять.
Из этого принципа также следует, что между направлением коммуникации и направлением электрического тока нет никакой зависимости. Многие люди ошибочно предполагают обратное, и это мешает им понять, как работает электроника.
Если нужно послать логический уровень «0», то обычно для этого напряжение на выводе передатчика понижают до 0 В, и из приёмника в передатчик начинает течь ток, чтобы приёмник смог определить, что логический уровень соответствует «0». (Тогда как обратное направление тока означало бы, что где-то в схеме присутствует отрицательный потенциал — а этого, как правило, в цифровой электронике не бывает.) С другой стороны, для передачи логического уровня «1» прикладывают напряжение, равное напряжению питания, а так как это, чаще всего, самое высокое напряжение в схеме, то электрическому току не останется ничего другого, как потечь из передатчика в приёмник.
Принцип номер два заключается в том, что невозможно определить состояние проводника, не изменив это состояние. Неважно, собрались ли вы измерять напряжение или ток — в любом случае, для этого необходимо, чтобы через ваш измерительный прибор потекли электроны. Поток электронов — это и есть электрический ток, а раз он течёт, то значит, что в узле, к которому вы подключились для измерения, токи и напряжение уже изменились (см. законы Кирхгофа). Из этого следует, что если вам нужно «передать» информацию, изменив состояние вывода, электрически связанного с другим выводом, то для этого требуется поддерживать данное состояние, а значит, соблюдать все требования, налагаемые приёмником.
Механическая кнопка (а в данном контексте слово «механическая» не связано со словосочетанием «механическая клавиатура») — это просто пара металлических контактов, которые, соприкасаясь, электрически соединяют два вывода. Конечно, бывают и другие типы переключателей, конструктивно более сложные и имеющие большее количество выводов, но нам они не интересны, потому что в клавиатурах не используются.

Кнопка Cherry MX. Источник изображения: Deskthority wiki
Ну, и как мы будем подключать кнопку ко входу микроконтроллера? Принципиально, любой вход может оперировать двумя возможными логическими уровнями: «0» и «1». Обычной практикой является принятие напряжений, близких к 0 В, за логический ноль, а напряжений, близких к напряжению питания (как правило, 5 В или 3,3 В) — за логическую единицу. Но проблема состоит в том, что управлять напряжением механическая кнопка сама по себе не может. Она управляет током — то есть, если мы соединим два узла с разным электрическим потенциалом через кнопку, то ток между этими узлами потечёт тогда и только тогда, когда кнопка будет нажата.
Но если мы добавим резистор, то очень просто сможем преобразовать ток в напряжение.
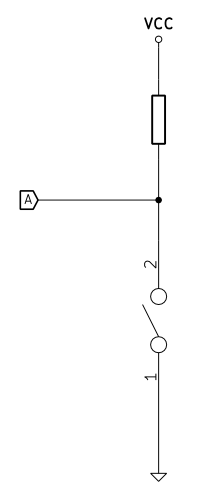
Кнопка с подтягивающим резистором
Взгляните на эту схему. Когда кнопка не нажата (цепь разорвана), ток через неё не течёт, поэтому напряжение в узле «A» будет близким к напряжению питания VCC (на самом деле, меньше VCC на величину падения напряжения на резисторе, равную R•I). Когда кнопка нажата (цепь замкнута), ток течёт через резистор на землю. С учётом того, что сопротивление замкнутой кнопки очень мало (порядка сотен миллиом), напряжение в узле «A» будет близким к «0».
В данной конфигурации резистор называют подтягивающим, потому что он «подтягивает напряжение вверх» до уровня VCC. А без подключения к питанию через резистор никакого напряжения в узле «A» вообще бы не было (в таком случае вывод микросхемы называют «висящим в воздухе» или находящимся в высокоимпедансном состоянии).
Необходимо отметить, что внутри у большинства современных микроконтроллеров уже присутствуют подтягивающие резисторы, которые можно оперативно подключать или отключать при помощи программы. Так что, основным способом соединения кнопки с микроконтроллером является следующий: один вывод кнопки — ко входу микроконтроллера, другой вывод кнопки — к земле. В таком случае, если кнопка не нажата, то на микроконтроллер подаётся «1», а если нажата, то «0». Возможно, это и противоречит интуиции, но данный способ подключения — самый популярный.
Обратите внимание, что если мы оставим один из выводов кнопки висящим в воздухе, то есть никуда его не подключим, то эта кнопка работать не будет вообще: сколько её не нажимай, она никак не повлияет на электрическое состояние вывода микроконтроллера. Мы ещё воспользуемся этим свойством, когда будем составлять матрицу.
Основным принципом клавиатурной матрицы является возможность подключать к одному входу микроконтроллера более одной кнопки.
При помощи транзисторов или правильно сконфигурированных выходов микроконтроллера мы можем сделать так, что кнопки к земле будут подключаться по одной, в то время как остальные будут висеть в воздухе. Оставшиеся выводы каждой из кнопок объединены в один узел и подключены ко входу микроконтроллера. Я опустил подтягивающий резистор, так как мы знаем, что он уже присутствует внутри микроконтроллера, в его входном каскаде. Мы по очереди «включаем» каждую кнопку, соединяя её вывод номер 1 с землёй через соответствующий выход микроконтроллера, после чего на входе мы можем прочесть состояние кнопки, сняв напряжение с её вывода номер 2. Другие кнопки, подключённые к этому же входу, не влияют на его состояние, потому что их выводы номер 1 в данный момент времени висят в воздухе. Следующая схема иллюстрирует эту идею.

Много кнопок, один вход (узел «A»)
«A» — это единственный вход микроконтроллера, а «C1»..«Cn» — его выходы. На одном из выходов установлен логический «0», то есть внутри микросхемы этот контакт каким-то образом соединён с землёй — следовательно, ток всегда будет течь к этому контакту (в соответствии с первым базовым принципом). Теперь, когда нажмётся кнопка, подключённая к данному выходу, то через неё вход «A» сразу же «придавится» к земле, и он установится в «0». Нажатия на другие кнопки ничего не изменят, потому что их земляные выводы в данный момент времени никуда не подключены. Когда нам потребуется опросить следующую кнопку, мы убираем с текущего выхода логический «0» и устанавливаем этот уровень на следующий выход, так что в любой момент времени будет задействован только один из выходов микроконтроллера.
Такая конфигурация (когда выход либо подключён к земле, либо вообще отключён) называется выходом с открытым стоком (ОС) (исторически — с открытым коллектором (ОК)). Здесь я допустил некоторое упрощение — на самом деле, контакт не может быть полностью отключён от схемы, если только он физически от неё не отрезан. Но для простого цифрового ввода-вывода такое упрощение вполне подходит. Большинство микроконтроллеров предоставляют возможность программной конфигурации своих выходных контактов для работы в режиме ОС. Но что, если у нас нет такой возможности? Существует и другая конфигурация — двухтактный режим; на сегодняшний день этот вариант — один из самых популярных. Работает такая конфигурация немного по-другому. В состоянии «0» выход всё так же придавлен к земле, но когда наступает состояние «1», он подтягивается к напряжению питания VCC, так что выход в воздухе больше не висит, теперь он сам может стать источником тока.
Какие изменения это повлечёт в конструкции матрицы? Если мы не собираемся нажимать несколько кнопок одновременно, то никаких. Но если собираемся, то взгляните на рисунок и представьте на секунду, что тогда произойдёт. Нажимая на две кнопки, мы соединяем два нижних выхода в замкнутый контур. Если при этом один из них в состоянии «0», а другой — в состоянии «1», то от выхода, установленного в «1», к выходу, установленному в «0», потечёт электрический ток. А так как этот ток ничем не ограничен (нет резисторов), то мало того, что схема станет нестабильной, так ещё и чип может вылететь. Ну и, само собой, вряд ли получится нормально считать логическое состояние.
Можете рассматривать предыдущий пример как матрицу, состоящую из одной строки. А теперь давайте увеличим её, нарастив дополнительные строки. В самом деле, если мы можем повесить на один вход целую строку, то почему мы не можем повесить на один выход целый столбец кнопок? Правда, есть обязательное условие — каждая кнопка столбца должна подключаться к отдельному входу микроконтроллера.
Если мы расположим кнопки в форме обычной матрицы, то это условие выполнится автоматически. А на следующем рисунке показано, как будет выглядеть матрица кнопок, состоящая из n столбцов и m строк (на зелёные фигуры внимания пока не обращайте).

Простая клавиатурная матрица
Считывать эту матрицу очень просто. Мы опрашиваем по одному столбцу за раз. Столбец для считывания выбирается путём соединения одного из выходов «C1»..«Cn» с землёй (выход в режиме ОС переводится в «0»). Теперь, поочерёдно опрашивая строки «R1»..«Rm», мы можем определить состояние каждой кнопки выбранного столбца. Кнопки из других столбцов ни на что не влияют, даже если они нажаты, потому что в данный момент их земляные выводы висят в воздухе (или, как говорят в электронике, находятся в состоянии Hi-Z).
После того, как будет опрошен весь столбец, мы переходим к следующему, отпустив текущий выход и придавив к нулю очередной. Сканирование матрицы считается оконченным, когда будут опрошены все столбцы. Если всё делать достаточно быстро, то интервалы между опросами столбцов не заметит и самый быстрый наборщик. Даже имея микроконтроллер 16 МГц, мы легко сможем сканировать всю матрицу тысячи раз в секунду, тогда как самый быстрый наборщик в тесте на hi-games.net добился скорости 203 слова в минуту (wpm) — то есть, чуть меньше, чем 17 нажатий в секунду.
Проектируя клавиатуру с использованием матрицы, мы уменьшаем количество выводов, требуемых для подключения всех клавиш. Но для того, чтобы свести число выводов к минимально возможному, нам надо составить матрицу таким образом, чтобы количество столбцов было как можно ближе к количеству строк. В идеальной ситуации, если количество кнопок равно n², то лучшее, чего мы сможем добиться при помощи матрицы — это 2n занятых выводов микроконтроллера. Однако сегодня при составлении матриц редко кто стремится максимально уменьшить количество задействованных ног, ведь современные микроконтроллеры, как правило, обладают достаточным количеством свободных выводов. Вдобавок, максимальная оптимизация матрицы может впоследствии привести к неудобствам — заметно усложнится разводка платы или распределение проводов в конечном устройстве. Поэтому стоит пойти более удобным путём: при составлении матрицы пытаться следовать физическому расположению кнопок. В таком случае, для стандартной компьютерной клавиатуры самая простая матрица будет иметь всего 6 строк и некоторое количество столбцов, в зависимости от желаемой компоновки. Конечно, с точки зрения количества задействованных выводов это решение — не самое оптимальное, но зато в дальнейшем хотя бы упростится разводка.
Вы можете спросить: а как нам быть, если в выбранном микроконтроллере всё-таки нет режима ОС? Ну, мы уже выяснили, какая неприятность может случиться, и что подтягивать выходы к VCC (то есть, «соединять» их с питанием) — не самая лучшая идея. Существует множество способов решения этой проблемы; среди них встречаются не только специальные выходные буферы ОС, но даже сдвиговые регистры с ОС-выходами — для ещё большей минимизации количества задействованных ног. Но есть и ещё один очень популярный приём, который довольно часто применяется в конструкциях компьютерных клавиатур (на самом деле, широко он применялся в былые времена).
Проблема подключённых к двухтактным выходам столбцов проявляется в тот момент, когда вместе нажимаются две кнопки, находящиеся в одной строке, причём одновременно с этим нажатием происходит опрос столбца, в котором расположена одна из кнопок.
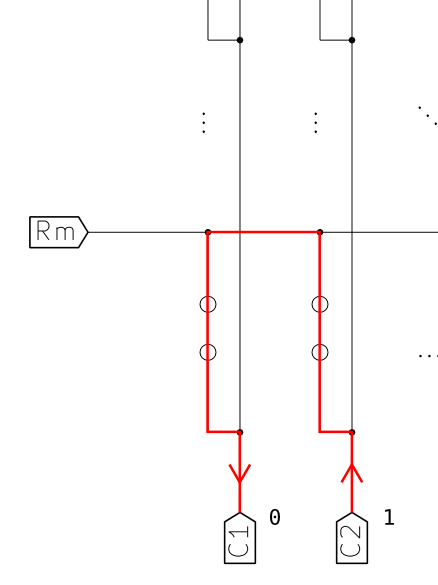
Проблема двухтактных выходов
Из выхода, который подтянут к «1» (а не висит в состоянии Hi-Z), начинает течь ток. Он проходит через ближайшую замкнутую кнопку, затем — через замкнутую кнопку в опрашиваемом столбце, и, наконец, втекает прямиком в выход, установленный в «0». Это может привести к чему угодно — начиная с невозможности надёжного считывания состояния клавиатуры и заканчивая выходом из строя самого микроконтроллера.
Но раз уж мы вынуждены как-то бороться с этой проблемой, то можем применить отличный трюк: превратить двухтактный выход в подобие выхода с открытым стоком. Я часто сталкивался с этим решением в конструкциях старых клавиатур. Учитывая, что ток должен только втекать в выходы (подключённые к столбцам), но никогда не вытекать из них, мы можем ограничить направление тока при помощи диодов. Диод — это простое устройство, которое позволяет току течь только в одном направлении. В изображении диода на электрической схеме треугольник символизирует стрелку, которая указывает это направление. Если поставить по диоду между каждым выходом микроконтроллера и проводником соответствующего столбца матрицы, то мы добьёмся поставленной цели — теперь ток может только втекать в выходы, ведь указанные проводники дотягиваются до каждой кнопки своего столбца. Получается, что из выхода, установленного в «1», ток никуда не потечёт, а это почти что превращает его в выход с открытым стоком. Конечно, до настоящего ОС он не дотягивает, но зато решает нашу проблему замкнутого токового контура в клавиатурной матрице. Вернитесь к предпоследнему рисунку матрицы, но на этот раз примите во внимание зелёные диоды, чтобы понять, как работает этот трюк.
Естественно, имеет смысл минимизировать количество диодов. Для этого можно уменьшить число столбцов, увеличив количество строк. А если получившийся результат плохо вписывается в реальную компоновку клавиатуры, то можно «развернуть» матрицу на 90° (поменять местами строки со столбцами). Возможности безграничны. Но в наши дни появилось огромное количество микроконтроллеров, которые просты в использовании и удобны для хоббистов, поэтому сегодня в проектах доморощенных клавиатур описанный приём уже практически не используется. К счастью.
Если вы интересуетесь клавами, то, должно быть, уже встречались с этим термином. К сожалению, в мире клавиатур его часто интерпретируют неправильно.
Мы уже знакомы с ситуацией, когда одновременное нажатие нескольких кнопок, находящихся в одной строке, может помешать нормальному считыванию матрицы. И эта проблема, можно сказать, нами решена. А теперь давайте посмотрим, что случится, если нажать несколько кнопок, находящихся одновременно в одной строке и в одном столбце.

Пример фантомного нажатия
На рисунке три кнопки нажаты одновременно. Две из них находятся в столбце «C2», и две — в строке «Rm». Это значит, что одна из нажатых кнопок делит строку с другой нажатой кнопкой, а столбец — с третьей нажатой кнопкой. Именно в такой ситуации и происходит фантомное нажатие. Представьте, что в данный момент мы опрашиваем столбец «C1» (то есть, он придавлен к земле — находится в состоянии «0»). Такой характерный аккорд нажатых кнопок приводит к следующему: даже несмотря на то, что левая верхняя кнопка не нажата, строка «R2» находится в состоянии «0», потому что она придавлена к земле столбцом «C1» (находящемся в «0») через три нажатые кнопки. В результате клавиатурный контроллер считывает левую верхнюю кнопку, как «нажатую», вне зависимости от того, нажата она на самом деле или нет. Описанная ситуация называется фантомным нажатием (ghosting), потому что некоторые комбинации одновременно нажатых кнопок вызывают фантомные срабатывания других кнопок (ghost keypresses), хотя физически эти другие кнопки и не нажаты.
Конечно, существуют способы оградить наборщиков и геймеров от фантомных срабатываний, и эти способы широко применяются в современных компьютерных клавиатурах. Можно поймать момент возникновения фантомного нажатия и заблокировать его. Обычный человек не в состоянии одновременно нажать или отпустить две клавиши с идеальной точностью. Поэтому, сканируя матрицу достаточно быстро, мы можем предположить, что между двумя проходами по матрице изменить своё состояние может не больше одной кнопки. В таком случае, контроллер принимает одиночные нажатия и следит за возникновением ситуаций, когда между проходами матрицы оказываются нажатыми две кнопки или более. Учитывая, что сканирование матрицы происходит со скоростью, при которой штатное возникновение таких ситуаций крайне маловероятно, можно заключить, что одна из только что нажатых кнопок — фантом. Поэтому контроллер должен проигнорировать все эти нажатия. Кроме того, безопаснее сразу не сообщать компьютеру об изменениях статуса клавиатуры — сначала имеет смысл подождать, пока все эти срабатывания не пропадут.
Есть и другой подход. Можно выявить ситуацию, когда срабатывает «третья» кнопка, и заблокировать как это нажатие, так и все последующие. Блокировку не снимать до тех пор, пока фантомное срабатывание не пропадёт, и ситуация опять не станет нормальной. Для реализации этого подхода программа должна помнить, какие именно кнопки сейчас нажаты (а обычно она это помнит и так), чтобы отклонять последующие срабатывания кнопок, в строках и в столбцах которых уже зафиксированы одновременные нажатия. Если написать программу с умом, то блокироваться будут только проблемные срабатывания, а все последующие будут приниматься как обычно — кроме тех, что снова нарушат правила. Раз контроллер отвергает нажатие каждой кнопки, уже имеющей одновременные срабатывания в своей строке и столбце, то выходит, что в зависимости от статуса одних кнопок, другие могут не регистрироваться вообще. Эта ситуация широко известна как блокирование (jamming). То есть кнопки, которые препятствуют одновременным срабатываниям других кнопок, получается, «блокируют» часть клавиатуры.
С точки зрения пользователя, можно одновременно нажать все кнопки из одного столбца (не нажимая кнопок из другого), но одновременно нажать все кнопки из одной строки можно только в том случае, если в столбце у каждой из этих кнопок зафиксировано не более одного срабатывания. То же самое относится и к нажатию кнопок из одного столбца — дополнительные срабатывания фиксируются только в том случае, если кнопки находятся в строках, которые «не заняты».
Люди часто путают «фантомное срабатывание» и «блокирование срабатывания» («ghosting» и «jamming»), что лично для меня является загадкой — по-моему, эти термины вполне интуитивны.
В клавиатурах с использованием таких матриц, как мы только что рассмотрели, невозможно избежать ни фантомных срабатываний, ни блокирования. Поскольку фантомные срабатывания в повседневной работе недопустимы, то для борьбы с ними практически все производители резинокупольных клавиатур пускают в ход различные ухищрения, и в игру вступает блокирование. Вопрос: как составить матрицу таким образом, чтобы блокирование возникало как можно реже и не вызывалось бы распространёнными клавиатурными комбинациями? На самом деле, это — хорошая тема для целой книги; именно поэтому матрицы ширпотребовских клавиатур такие запутанные и всегда блокируют хорошее настроение (типа, каламбур).
Если вы ещё раз взглянете на картинку про фантомные нажатия, то сможете заметить, что во всём виновата правая нижняя кнопка.
А ведь эта кнопка — единственная, через которую ток в данной ситуации течёт «вверх». Так что, если мы не хотим, чтобы текущие «вверх» токи мешали нам нормально считывать матрицу, то давайте введём диоды, чтобы ток мог идти по столбцам строго сверху вниз, втекая в выходы микроконтроллера.
К сожалению, сэкономить тут не получится — придётся ставить по диоду на каждую кнопку. Если же говорить о полярности, то вы уже должны были разобраться, что в данном конкретном случае диоды должны пропускать ток «сверху вниз», то есть их катоды («кончики стрелок») должны смотреть на выходы микроконтроллера (столбцы), тогда как аноды должны быть обращены ко входам (строкам).

Итоговая матрица
Не имеет значения, с какой стороны кнопки располагать диод; главное — соблюсти верную полярность. Просто запомните, что в данном случае ток всегда будет течь от входов к выходам. К слову, если входы подтянуты к питанию, а выходы — в режиме ОС, то так происходить будет всегда.
При данном подходе получается, что ток всегда будет течь «вправо вниз», и это исключает появление замкнутых токовых контуров при одновременном нажатии нескольких кнопок. Кроме того, эта конструкция — единственная, которая может обеспечить клавиатуре полный NKRO. Вдобавок, нелишним будет упомянуть (хотя это и кажется очевидным), что проблема отсутствия у выходов микроконтроллера режима ОС решается теперь автоматически. Диоды, установленные последовательно с каждой кнопкой, избавляют выходы от замыкания не хуже рассмотренного ранее варианта, где предполагалось дополнительно ставить по диоду на каждый столбец.
Да, я знаю, что текст и так уже слишком длинный. Но я всё-таки добавлю эту последнюю главу, потому что, по-моему, без неё статья будет неполной. Так вот, ролловер — это способность клавиатуры воспринимать несколько нажатий одновременно.
KRO означает клавишный ролловер (key rollover), и обычно эта аббревиатура озаглавлена каким-то числом. Например, 2KRO означает двухклавишный ролловер. Клавиатура обладает x-клавишным ролловером тогда и только тогда, когда она способна зарегистрировать x одновременных нажатий, причём — вне зависимости от того, какие кнопки и в какой последовательности были задействованы. Большинство современных резинокупольных клавиатур обладают 2KRO. Из этого, однако, не следует, что допустимое количество нажатий у этих клавиатур всегда будет ограничено числом x. На самом деле это означает, что поддержка x одновременных нажатий гарантируется точно.
В зависимости от конструкции матрицы и от типа контроллера, две клавиатуры 2KRO от разных производителей могут вести себя совершенно по-разному. Одна может всегда воспринимать только два одновременных нажатия, а другая с лёгкостью переварит и больше. Думается, последняя клавиатура была заявлена 2KRO потому, что некоторые комбинации клавиш (скорее всего, маловероятные) всё-таки будут вызывать у неё блокирование нажатий других кнопок. А так как это означает, что при работе с данной клавиатурой определённые комбинации из трёх клавиш и более срабатывать не будут, то компания и объявила её 2KRO.
Термин NKRO означает N-клавишный ролловер, и его используют для обозначения клавиатур, поддерживающих, несмотря ни на что, любую комбинацию одновременно нажатых клавиш. Но имейте в виду, что NKRO матрицы и NKRO клавиатуры — это две большие разницы. К примеру, если итоговая реализация матрицы, рассмотренная нами в статье, поддерживает NKRO (с учётом корректно написанной прошивки), то из этого совсем не следует, что клавиатура, использующая данную матрицу, тоже будет поддерживать NKRO. Это может происходить из-за ограничений, накладываемых коммуникационными портами, к которым подключается клавиатура; другой причиной может стать бережливость производителей, вечно экономящих то здесь, то там. Проблему NKRO при соединении с PS/2 и USB я попытаюсь разъяснить в следующих частях.
Конечно, простыня вышла изрядная, но ведь концепция не такая уж и простая — особенно для читателя, который не является инженером-электронщиком. Надеюсь, мне удалось всё объяснить; как бы то ни было, писать я старался как можно понятнее. Поэтому кому-то из вас статья могла показаться довольно скучной. Ну, а если вы шарите в электронике, то, скорее всего, читать вам её вообще не стоило ;)
В любом случае, пожалуйста, дайте мне знать, оказалась ли статья для вас полезной и стоит ли писать продолжение. Если да, то засяду за следующую «серию».
Michał Trybus
2 сентября 2013
Оригинал: blog.komar.be/how-to-make-a-keyboard-the-matrix
Это — первый пост из серии, посвящённой клавиатурам; надеюсь, он не будет последним. Хочется, чтобы в итоге получился курс по изготовлению клавиатуры с нуля. Сегодня я расскажу о цифровом вводе-выводе и о клавиатурных матрицах. Вооружитесь элементарными школьными знаниями из области электроники — и поехали.
Почему матрица?
И как же мы собираемся делать матрицу? А самое главное — зачем она вообще нужна? Ну, виной тому, в основном, физические ограничения микроконтроллеров, на базе которых строятся клавиатуры. Дело в том, что с увеличением количества выводов у микроконтроллеров и программируемых логических микросхем растёт и их размер, что, в свою очередь, влечёт за собой рост энергопотребления, возможностей, но главное — цены. В итоге, вы можете выбрать либо дешёвый чип с небольшой производительностью (которая вас вполне устраивает), но с малым количеством входов и выходов, либо более мощную микросхему, производительность которой, однако, сильно превышает ваши требования. Но только этот мощный чип будет обладать достаточным количеством выводов, чтобы подключить каждую кнопку клавиатуры.
За десятилетия в электронике сложилась практика при помощи различных ухищрений искусственно расширять встроенные коммуникационные возможности процессоров и контроллеров. Одним из таких способов, который хорошо подходит для механических контактов (кнопок), и является создание матрицы. Чтобы понять, как она работает, требуются некоторые базовые знания. Прежде, чем мы продолжим, пожалуйста, освежите в памяти закон Ома.
Немного теории
Чтобы разобраться, как работает цифровая электроника, надо усвоить два базовых принципа.
Принцип первый гласит, что процесс коммуникации внутри схемы — это не передача или получение чего-то там. Чтобы обеспечить коммуникацию между двумя устройствами, вы просто соединяете между собой их выводы электропроводящим материалом. После этого предполагается, что состояние материала (напряжение и ток) на обоих его концах будет одинаковым. В реальности это, конечно, не так, но для медленных коммуникаций и коротких проводников наше предположение работает отлично. Выходит, что посылка и получение информации на самом деле является её совместным использованием.
Со стороны передатчика вы просто изменяете электрическое состояние проводника (запуская в него постоянный ток, изменяя его потенциал), рассчитывая на то, что приёмник сможет определить это изменение и правильно его понять.
Из этого принципа также следует, что между направлением коммуникации и направлением электрического тока нет никакой зависимости. Многие люди ошибочно предполагают обратное, и это мешает им понять, как работает электроника.
Если нужно послать логический уровень «0», то обычно для этого напряжение на выводе передатчика понижают до 0 В, и из приёмника в передатчик начинает течь ток, чтобы приёмник смог определить, что логический уровень соответствует «0». (Тогда как обратное направление тока означало бы, что где-то в схеме присутствует отрицательный потенциал — а этого, как правило, в цифровой электронике не бывает.) С другой стороны, для передачи логического уровня «1» прикладывают напряжение, равное напряжению питания, а так как это, чаще всего, самое высокое напряжение в схеме, то электрическому току не останется ничего другого, как потечь из передатчика в приёмник.
Принцип номер два заключается в том, что невозможно определить состояние проводника, не изменив это состояние. Неважно, собрались ли вы измерять напряжение или ток — в любом случае, для этого необходимо, чтобы через ваш измерительный прибор потекли электроны. Поток электронов — это и есть электрический ток, а раз он течёт, то значит, что в узле, к которому вы подключились для измерения, токи и напряжение уже изменились (см. законы Кирхгофа). Из этого следует, что если вам нужно «передать» информацию, изменив состояние вывода, электрически связанного с другим выводом, то для этого требуется поддерживать данное состояние, а значит, соблюдать все требования, налагаемые приёмником.
Кнопка
Механическая кнопка (а в данном контексте слово «механическая» не связано со словосочетанием «механическая клавиатура») — это просто пара металлических контактов, которые, соприкасаясь, электрически соединяют два вывода. Конечно, бывают и другие типы переключателей, конструктивно более сложные и имеющие большее количество выводов, но нам они не интересны, потому что в клавиатурах не используются.

Кнопка Cherry MX. Источник изображения: Deskthority wiki
Ну, и как мы будем подключать кнопку ко входу микроконтроллера? Принципиально, любой вход может оперировать двумя возможными логическими уровнями: «0» и «1». Обычной практикой является принятие напряжений, близких к 0 В, за логический ноль, а напряжений, близких к напряжению питания (как правило, 5 В или 3,3 В) — за логическую единицу. Но проблема состоит в том, что управлять напряжением механическая кнопка сама по себе не может. Она управляет током — то есть, если мы соединим два узла с разным электрическим потенциалом через кнопку, то ток между этими узлами потечёт тогда и только тогда, когда кнопка будет нажата.
Но если мы добавим резистор, то очень просто сможем преобразовать ток в напряжение.

Кнопка с подтягивающим резистором
Взгляните на эту схему. Когда кнопка не нажата (цепь разорвана), ток через неё не течёт, поэтому напряжение в узле «A» будет близким к напряжению питания VCC (на самом деле, меньше VCC на величину падения напряжения на резисторе, равную R•I). Когда кнопка нажата (цепь замкнута), ток течёт через резистор на землю. С учётом того, что сопротивление замкнутой кнопки очень мало (порядка сотен миллиом), напряжение в узле «A» будет близким к «0».
В данной конфигурации резистор называют подтягивающим, потому что он «подтягивает напряжение вверх» до уровня VCC. А без подключения к питанию через резистор никакого напряжения в узле «A» вообще бы не было (в таком случае вывод микросхемы называют «висящим в воздухе» или находящимся в высокоимпедансном состоянии).
Необходимо отметить, что внутри у большинства современных микроконтроллеров уже присутствуют подтягивающие резисторы, которые можно оперативно подключать или отключать при помощи программы. Так что, основным способом соединения кнопки с микроконтроллером является следующий: один вывод кнопки — ко входу микроконтроллера, другой вывод кнопки — к земле. В таком случае, если кнопка не нажата, то на микроконтроллер подаётся «1», а если нажата, то «0». Возможно, это и противоречит интуиции, но данный способ подключения — самый популярный.
Обратите внимание, что если мы оставим один из выводов кнопки висящим в воздухе, то есть никуда его не подключим, то эта кнопка работать не будет вообще: сколько её не нажимай, она никак не повлияет на электрическое состояние вывода микроконтроллера. Мы ещё воспользуемся этим свойством, когда будем составлять матрицу.
Принцип матрицы
Основным принципом клавиатурной матрицы является возможность подключать к одному входу микроконтроллера более одной кнопки.
При помощи транзисторов или правильно сконфигурированных выходов микроконтроллера мы можем сделать так, что кнопки к земле будут подключаться по одной, в то время как остальные будут висеть в воздухе. Оставшиеся выводы каждой из кнопок объединены в один узел и подключены ко входу микроконтроллера. Я опустил подтягивающий резистор, так как мы знаем, что он уже присутствует внутри микроконтроллера, в его входном каскаде. Мы по очереди «включаем» каждую кнопку, соединяя её вывод номер 1 с землёй через соответствующий выход микроконтроллера, после чего на входе мы можем прочесть состояние кнопки, сняв напряжение с её вывода номер 2. Другие кнопки, подключённые к этому же входу, не влияют на его состояние, потому что их выводы номер 1 в данный момент времени висят в воздухе. Следующая схема иллюстрирует эту идею.

Много кнопок, один вход (узел «A»)
«A» — это единственный вход микроконтроллера, а «C1»..«Cn» — его выходы. На одном из выходов установлен логический «0», то есть внутри микросхемы этот контакт каким-то образом соединён с землёй — следовательно, ток всегда будет течь к этому контакту (в соответствии с первым базовым принципом). Теперь, когда нажмётся кнопка, подключённая к данному выходу, то через неё вход «A» сразу же «придавится» к земле, и он установится в «0». Нажатия на другие кнопки ничего не изменят, потому что их земляные выводы в данный момент времени никуда не подключены. Когда нам потребуется опросить следующую кнопку, мы убираем с текущего выхода логический «0» и устанавливаем этот уровень на следующий выход, так что в любой момент времени будет задействован только один из выходов микроконтроллера.
Такая конфигурация (когда выход либо подключён к земле, либо вообще отключён) называется выходом с открытым стоком (ОС) (исторически — с открытым коллектором (ОК)). Здесь я допустил некоторое упрощение — на самом деле, контакт не может быть полностью отключён от схемы, если только он физически от неё не отрезан. Но для простого цифрового ввода-вывода такое упрощение вполне подходит. Большинство микроконтроллеров предоставляют возможность программной конфигурации своих выходных контактов для работы в режиме ОС. Но что, если у нас нет такой возможности? Существует и другая конфигурация — двухтактный режим; на сегодняшний день этот вариант — один из самых популярных. Работает такая конфигурация немного по-другому. В состоянии «0» выход всё так же придавлен к земле, но когда наступает состояние «1», он подтягивается к напряжению питания VCC, так что выход в воздухе больше не висит, теперь он сам может стать источником тока.
Какие изменения это повлечёт в конструкции матрицы? Если мы не собираемся нажимать несколько кнопок одновременно, то никаких. Но если собираемся, то взгляните на рисунок и представьте на секунду, что тогда произойдёт. Нажимая на две кнопки, мы соединяем два нижних выхода в замкнутый контур. Если при этом один из них в состоянии «0», а другой — в состоянии «1», то от выхода, установленного в «1», к выходу, установленному в «0», потечёт электрический ток. А так как этот ток ничем не ограничен (нет резисторов), то мало того, что схема станет нестабильной, так ещё и чип может вылететь. Ну и, само собой, вряд ли получится нормально считать логическое состояние.
Добавление строк
Можете рассматривать предыдущий пример как матрицу, состоящую из одной строки. А теперь давайте увеличим её, нарастив дополнительные строки. В самом деле, если мы можем повесить на один вход целую строку, то почему мы не можем повесить на один выход целый столбец кнопок? Правда, есть обязательное условие — каждая кнопка столбца должна подключаться к отдельному входу микроконтроллера.
Если мы расположим кнопки в форме обычной матрицы, то это условие выполнится автоматически. А на следующем рисунке показано, как будет выглядеть матрица кнопок, состоящая из n столбцов и m строк (на зелёные фигуры внимания пока не обращайте).

Простая клавиатурная матрица
Считывать эту матрицу очень просто. Мы опрашиваем по одному столбцу за раз. Столбец для считывания выбирается путём соединения одного из выходов «C1»..«Cn» с землёй (выход в режиме ОС переводится в «0»). Теперь, поочерёдно опрашивая строки «R1»..«Rm», мы можем определить состояние каждой кнопки выбранного столбца. Кнопки из других столбцов ни на что не влияют, даже если они нажаты, потому что в данный момент их земляные выводы висят в воздухе (или, как говорят в электронике, находятся в состоянии Hi-Z).
После того, как будет опрошен весь столбец, мы переходим к следующему, отпустив текущий выход и придавив к нулю очередной. Сканирование матрицы считается оконченным, когда будут опрошены все столбцы. Если всё делать достаточно быстро, то интервалы между опросами столбцов не заметит и самый быстрый наборщик. Даже имея микроконтроллер 16 МГц, мы легко сможем сканировать всю матрицу тысячи раз в секунду, тогда как самый быстрый наборщик в тесте на hi-games.net добился скорости 203 слова в минуту (wpm) — то есть, чуть меньше, чем 17 нажатий в секунду.
Проектируя клавиатуру с использованием матрицы, мы уменьшаем количество выводов, требуемых для подключения всех клавиш. Но для того, чтобы свести число выводов к минимально возможному, нам надо составить матрицу таким образом, чтобы количество столбцов было как можно ближе к количеству строк. В идеальной ситуации, если количество кнопок равно n², то лучшее, чего мы сможем добиться при помощи матрицы — это 2n занятых выводов микроконтроллера. Однако сегодня при составлении матриц редко кто стремится максимально уменьшить количество задействованных ног, ведь современные микроконтроллеры, как правило, обладают достаточным количеством свободных выводов. Вдобавок, максимальная оптимизация матрицы может впоследствии привести к неудобствам — заметно усложнится разводка платы или распределение проводов в конечном устройстве. Поэтому стоит пойти более удобным путём: при составлении матрицы пытаться следовать физическому расположению кнопок. В таком случае, для стандартной компьютерной клавиатуры самая простая матрица будет иметь всего 6 строк и некоторое количество столбцов, в зависимости от желаемой компоновки. Конечно, с точки зрения количества задействованных выводов это решение — не самое оптимальное, но зато в дальнейшем хотя бы упростится разводка.
А что, если выходов с открытым стоком у нас нет?
Вы можете спросить: а как нам быть, если в выбранном микроконтроллере всё-таки нет режима ОС? Ну, мы уже выяснили, какая неприятность может случиться, и что подтягивать выходы к VCC (то есть, «соединять» их с питанием) — не самая лучшая идея. Существует множество способов решения этой проблемы; среди них встречаются не только специальные выходные буферы ОС, но даже сдвиговые регистры с ОС-выходами — для ещё большей минимизации количества задействованных ног. Но есть и ещё один очень популярный приём, который довольно часто применяется в конструкциях компьютерных клавиатур (на самом деле, широко он применялся в былые времена).
Проблема подключённых к двухтактным выходам столбцов проявляется в тот момент, когда вместе нажимаются две кнопки, находящиеся в одной строке, причём одновременно с этим нажатием происходит опрос столбца, в котором расположена одна из кнопок.

Проблема двухтактных выходов
Из выхода, который подтянут к «1» (а не висит в состоянии Hi-Z), начинает течь ток. Он проходит через ближайшую замкнутую кнопку, затем — через замкнутую кнопку в опрашиваемом столбце, и, наконец, втекает прямиком в выход, установленный в «0». Это может привести к чему угодно — начиная с невозможности надёжного считывания состояния клавиатуры и заканчивая выходом из строя самого микроконтроллера.
Но раз уж мы вынуждены как-то бороться с этой проблемой, то можем применить отличный трюк: превратить двухтактный выход в подобие выхода с открытым стоком. Я часто сталкивался с этим решением в конструкциях старых клавиатур. Учитывая, что ток должен только втекать в выходы (подключённые к столбцам), но никогда не вытекать из них, мы можем ограничить направление тока при помощи диодов. Диод — это простое устройство, которое позволяет току течь только в одном направлении. В изображении диода на электрической схеме треугольник символизирует стрелку, которая указывает это направление. Если поставить по диоду между каждым выходом микроконтроллера и проводником соответствующего столбца матрицы, то мы добьёмся поставленной цели — теперь ток может только втекать в выходы, ведь указанные проводники дотягиваются до каждой кнопки своего столбца. Получается, что из выхода, установленного в «1», ток никуда не потечёт, а это почти что превращает его в выход с открытым стоком. Конечно, до настоящего ОС он не дотягивает, но зато решает нашу проблему замкнутого токового контура в клавиатурной матрице. Вернитесь к предпоследнему рисунку матрицы, но на этот раз примите во внимание зелёные диоды, чтобы понять, как работает этот трюк.
Естественно, имеет смысл минимизировать количество диодов. Для этого можно уменьшить число столбцов, увеличив количество строк. А если получившийся результат плохо вписывается в реальную компоновку клавиатуры, то можно «развернуть» матрицу на 90° (поменять местами строки со столбцами). Возможности безграничны. Но в наши дни появилось огромное количество микроконтроллеров, которые просты в использовании и удобны для хоббистов, поэтому сегодня в проектах доморощенных клавиатур описанный приём уже практически не используется. К счастью.
Фантомные нажатия (Ghosting)
Если вы интересуетесь клавами, то, должно быть, уже встречались с этим термином. К сожалению, в мире клавиатур его часто интерпретируют неправильно.
Мы уже знакомы с ситуацией, когда одновременное нажатие нескольких кнопок, находящихся в одной строке, может помешать нормальному считыванию матрицы. И эта проблема, можно сказать, нами решена. А теперь давайте посмотрим, что случится, если нажать несколько кнопок, находящихся одновременно в одной строке и в одном столбце.

Пример фантомного нажатия
На рисунке три кнопки нажаты одновременно. Две из них находятся в столбце «C2», и две — в строке «Rm». Это значит, что одна из нажатых кнопок делит строку с другой нажатой кнопкой, а столбец — с третьей нажатой кнопкой. Именно в такой ситуации и происходит фантомное нажатие. Представьте, что в данный момент мы опрашиваем столбец «C1» (то есть, он придавлен к земле — находится в состоянии «0»). Такой характерный аккорд нажатых кнопок приводит к следующему: даже несмотря на то, что левая верхняя кнопка не нажата, строка «R2» находится в состоянии «0», потому что она придавлена к земле столбцом «C1» (находящемся в «0») через три нажатые кнопки. В результате клавиатурный контроллер считывает левую верхнюю кнопку, как «нажатую», вне зависимости от того, нажата она на самом деле или нет. Описанная ситуация называется фантомным нажатием (ghosting), потому что некоторые комбинации одновременно нажатых кнопок вызывают фантомные срабатывания других кнопок (ghost keypresses), хотя физически эти другие кнопки и не нажаты.
Конечно, существуют способы оградить наборщиков и геймеров от фантомных срабатываний, и эти способы широко применяются в современных компьютерных клавиатурах. Можно поймать момент возникновения фантомного нажатия и заблокировать его. Обычный человек не в состоянии одновременно нажать или отпустить две клавиши с идеальной точностью. Поэтому, сканируя матрицу достаточно быстро, мы можем предположить, что между двумя проходами по матрице изменить своё состояние может не больше одной кнопки. В таком случае, контроллер принимает одиночные нажатия и следит за возникновением ситуаций, когда между проходами матрицы оказываются нажатыми две кнопки или более. Учитывая, что сканирование матрицы происходит со скоростью, при которой штатное возникновение таких ситуаций крайне маловероятно, можно заключить, что одна из только что нажатых кнопок — фантом. Поэтому контроллер должен проигнорировать все эти нажатия. Кроме того, безопаснее сразу не сообщать компьютеру об изменениях статуса клавиатуры — сначала имеет смысл подождать, пока все эти срабатывания не пропадут.
Есть и другой подход. Можно выявить ситуацию, когда срабатывает «третья» кнопка, и заблокировать как это нажатие, так и все последующие. Блокировку не снимать до тех пор, пока фантомное срабатывание не пропадёт, и ситуация опять не станет нормальной. Для реализации этого подхода программа должна помнить, какие именно кнопки сейчас нажаты (а обычно она это помнит и так), чтобы отклонять последующие срабатывания кнопок, в строках и в столбцах которых уже зафиксированы одновременные нажатия. Если написать программу с умом, то блокироваться будут только проблемные срабатывания, а все последующие будут приниматься как обычно — кроме тех, что снова нарушат правила. Раз контроллер отвергает нажатие каждой кнопки, уже имеющей одновременные срабатывания в своей строке и столбце, то выходит, что в зависимости от статуса одних кнопок, другие могут не регистрироваться вообще. Эта ситуация широко известна как блокирование (jamming). То есть кнопки, которые препятствуют одновременным срабатываниям других кнопок, получается, «блокируют» часть клавиатуры.
С точки зрения пользователя, можно одновременно нажать все кнопки из одного столбца (не нажимая кнопок из другого), но одновременно нажать все кнопки из одной строки можно только в том случае, если в столбце у каждой из этих кнопок зафиксировано не более одного срабатывания. То же самое относится и к нажатию кнопок из одного столбца — дополнительные срабатывания фиксируются только в том случае, если кнопки находятся в строках, которые «не заняты».
Люди часто путают «фантомное срабатывание» и «блокирование срабатывания» («ghosting» и «jamming»), что лично для меня является загадкой — по-моему, эти термины вполне интуитивны.
В клавиатурах с использованием таких матриц, как мы только что рассмотрели, невозможно избежать ни фантомных срабатываний, ни блокирования. Поскольку фантомные срабатывания в повседневной работе недопустимы, то для борьбы с ними практически все производители резинокупольных клавиатур пускают в ход различные ухищрения, и в игру вступает блокирование. Вопрос: как составить матрицу таким образом, чтобы блокирование возникало как можно реже и не вызывалось бы распространёнными клавиатурными комбинациями? На самом деле, это — хорошая тема для целой книги; именно поэтому матрицы ширпотребовских клавиатур такие запутанные и всегда блокируют хорошее настроение (типа, каламбур).
Диоды на все кнопки — кардинальное решение
Если вы ещё раз взглянете на картинку про фантомные нажатия, то сможете заметить, что во всём виновата правая нижняя кнопка.
А ведь эта кнопка — единственная, через которую ток в данной ситуации течёт «вверх». Так что, если мы не хотим, чтобы текущие «вверх» токи мешали нам нормально считывать матрицу, то давайте введём диоды, чтобы ток мог идти по столбцам строго сверху вниз, втекая в выходы микроконтроллера.
К сожалению, сэкономить тут не получится — придётся ставить по диоду на каждую кнопку. Если же говорить о полярности, то вы уже должны были разобраться, что в данном конкретном случае диоды должны пропускать ток «сверху вниз», то есть их катоды («кончики стрелок») должны смотреть на выходы микроконтроллера (столбцы), тогда как аноды должны быть обращены ко входам (строкам).

Итоговая матрица
Не имеет значения, с какой стороны кнопки располагать диод; главное — соблюсти верную полярность. Просто запомните, что в данном случае ток всегда будет течь от входов к выходам. К слову, если входы подтянуты к питанию, а выходы — в режиме ОС, то так происходить будет всегда.
При данном подходе получается, что ток всегда будет течь «вправо вниз», и это исключает появление замкнутых токовых контуров при одновременном нажатии нескольких кнопок. Кроме того, эта конструкция — единственная, которая может обеспечить клавиатуре полный NKRO. Вдобавок, нелишним будет упомянуть (хотя это и кажется очевидным), что проблема отсутствия у выходов микроконтроллера режима ОС решается теперь автоматически. Диоды, установленные последовательно с каждой кнопкой, избавляют выходы от замыкания не хуже рассмотренного ранее варианта, где предполагалось дополнительно ставить по диоду на каждый столбец.
Ролловер (Rollover)
Да, я знаю, что текст и так уже слишком длинный. Но я всё-таки добавлю эту последнюю главу, потому что, по-моему, без неё статья будет неполной. Так вот, ролловер — это способность клавиатуры воспринимать несколько нажатий одновременно.
xKRO
KRO означает клавишный ролловер (key rollover), и обычно эта аббревиатура озаглавлена каким-то числом. Например, 2KRO означает двухклавишный ролловер. Клавиатура обладает x-клавишным ролловером тогда и только тогда, когда она способна зарегистрировать x одновременных нажатий, причём — вне зависимости от того, какие кнопки и в какой последовательности были задействованы. Большинство современных резинокупольных клавиатур обладают 2KRO. Из этого, однако, не следует, что допустимое количество нажатий у этих клавиатур всегда будет ограничено числом x. На самом деле это означает, что поддержка x одновременных нажатий гарантируется точно.
В зависимости от конструкции матрицы и от типа контроллера, две клавиатуры 2KRO от разных производителей могут вести себя совершенно по-разному. Одна может всегда воспринимать только два одновременных нажатия, а другая с лёгкостью переварит и больше. Думается, последняя клавиатура была заявлена 2KRO потому, что некоторые комбинации клавиш (скорее всего, маловероятные) всё-таки будут вызывать у неё блокирование нажатий других кнопок. А так как это означает, что при работе с данной клавиатурой определённые комбинации из трёх клавиш и более срабатывать не будут, то компания и объявила её 2KRO.
NKRO
Термин NKRO означает N-клавишный ролловер, и его используют для обозначения клавиатур, поддерживающих, несмотря ни на что, любую комбинацию одновременно нажатых клавиш. Но имейте в виду, что NKRO матрицы и NKRO клавиатуры — это две большие разницы. К примеру, если итоговая реализация матрицы, рассмотренная нами в статье, поддерживает NKRO (с учётом корректно написанной прошивки), то из этого совсем не следует, что клавиатура, использующая данную матрицу, тоже будет поддерживать NKRO. Это может происходить из-за ограничений, накладываемых коммуникационными портами, к которым подключается клавиатура; другой причиной может стать бережливость производителей, вечно экономящих то здесь, то там. Проблему NKRO при соединении с PS/2 и USB я попытаюсь разъяснить в следующих частях.
Итог
Конечно, простыня вышла изрядная, но ведь концепция не такая уж и простая — особенно для читателя, который не является инженером-электронщиком. Надеюсь, мне удалось всё объяснить; как бы то ни было, писать я старался как можно понятнее. Поэтому кому-то из вас статья могла показаться довольно скучной. Ну, а если вы шарите в электронике, то, скорее всего, читать вам её вообще не стоило ;)
В любом случае, пожалуйста, дайте мне знать, оказалась ли статья для вас полезной и стоит ли писать продолжение. Если да, то засяду за следующую «серию».
Michał Trybus
2 сентября 2013