Вся правда о новейшей вирусной задачке из Сингапура и ещё одной исторической загадке с числами

В честь юбилея этой колонки интернет любезно предоставил мне сингапурскую математическую задачку, ставшую вирусной. В середине мая веб был взволнован задачей, которую, якобы дают решать первоклассникам Сингапура, а это дети возрастом от 5 до 7 лет, и которая оказалась настолько сложной, что никто не может её решить.

Внимательно изучите последовательность цифр и заполните пробелы
Но наша история на самом деле про то, как фразы вроде «математическая задачка всколыхнула интернет» стали скучными и предсказуемыми попытками привлечь посетителей на страницу. Поскольку даже краткий взгляд на этот вопрос, который впервые появился на техническом форуме Сингапура, позволяет сказать, что это фото – очевидная подделка. Фотография выглядит отредактированной, а к задаче нет пояснений.
Судя по всему, задачку взяли (и видоизменили) с сайта, посвящённого математическим головоломкам, который ведёт Гордон Бёрджин, американский учитель на пенсии. И в варианте с сайта в левой нижней четверти стоит цифра 20. В сингапурской фотке 0 замазан. Неудивительно, что там нет очевидного решения!
«Я поражён этой подделкой и не знаю, чего они пытались этим достичь, – говорит Бёрджин. – Если их целью было бурное обсуждение и последующее отчаяние, то они своего добились!»
Далее идёт правильный вариант загадки.
1. В каждом из четырёх секторов внешнего круга находится двузначное число, равное сумме трёх чисел, расположенных в углах этого сектора. Числа в отдельных кружках могут меняться от 1 до 9, и каждое из чисел может быть использовано только один раз. Одно из чисел дано вам для того, чтобы начать. Найдите оставшиеся четыре.
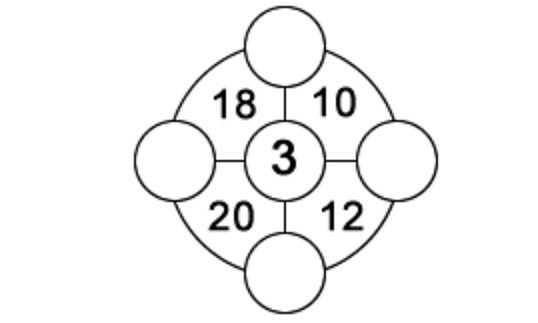
2. Поскольку сингапурская загадка была неправильная – попробуйте предложить вариант задачи, который бы подошёл для приведённой картинки (с затёртым нулём).
Эта загадка напомнила мне задачку из одной из самых интересных книг по истории загадок: "Wakoku chiekurabe", старейшую японскую книгу загадок, опубликованную в 1727 году. Это прекрасная загадка – и, по меньшей мере, она-то как раз родилась на Востоке!
3. Запишите числа от 1 до 9 в чёрных кружочках так, чтобы сумма чисел, находящихся на каждом из двух голубых кругов (включая центральный кружок), а также вдоль горизонтальных и вертикальных линий была одинаковой.

Это четыре суммы, каждая из которых состоит из пяти слагаемых, и все суммы получаются одинаковыми. Вот картинка из самой книги, на которой изображена схожая задача.


1. По часовой стрелке, начиная сверху: 6, 1, 8, 9
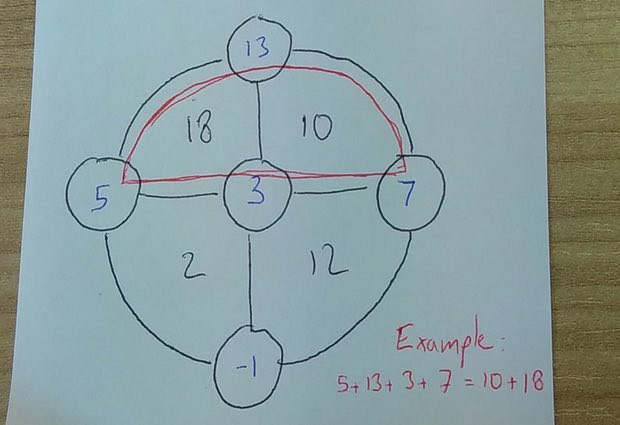
Если мы назовём позиции для чисел Север, Восток, Запад, и Юг, то кандидатами для Запада и Юга будут 8 и 9, поскольку Ю + З + 3 = 20, или Ю + З = 17. Но нам известно, что Ю + В + 3 = 12, или Ю + В = 9. Но Ю не может быть 9, поскольку тогда В = 0, а это запрещено. Поэтому Ю = 8, З = 9, С = 6 и В = 1.
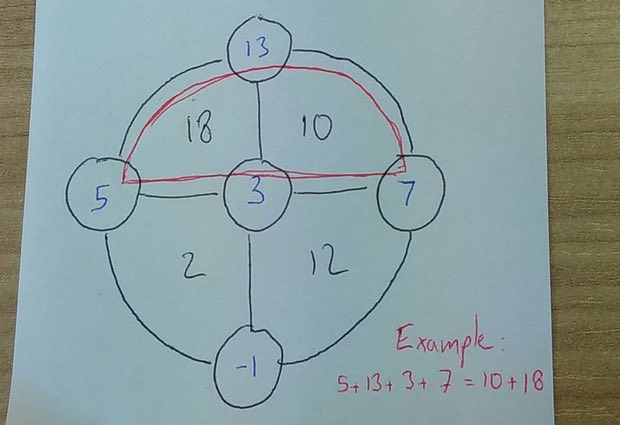
2. Мне больше всего понравилось задание, присланное читателем по имени Том Флэннери, поскольку оно оказалось очень простым.
3. И последняя задача, из японского сборника загадок 1727 года.
Решений может быть много. Вот моё решение:
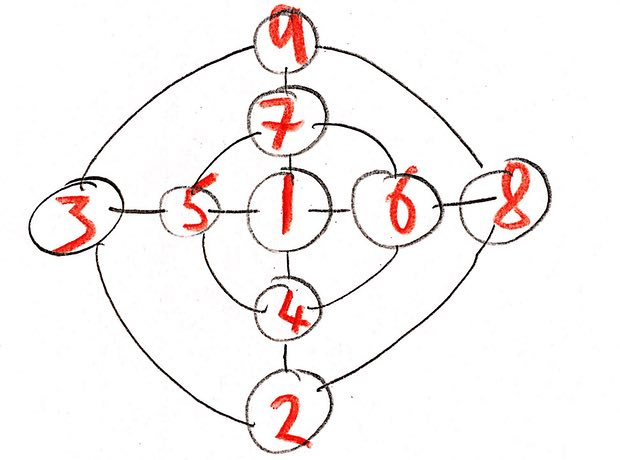
Путь к решению помогает проложить догадка – в центре может быть только нечётное число. Выбрав такое число, нужно разделить оставшиеся цифры на пары, которые в сумме дают одно и то же число, и расположить их в противоположных кружочках. Я выбрал 1 для центра, соответственно остаются пары 2 и 9, 3 и 8, 4 и 7, 5 и 6 – все они дают в сумме 11.

В честь юбилея этой колонки интернет любезно предоставил мне сингапурскую математическую задачку, ставшую вирусной. В середине мая веб был взволнован задачей, которую, якобы дают решать первоклассникам Сингапура, а это дети возрастом от 5 до 7 лет, и которая оказалась настолько сложной, что никто не может её решить.

Внимательно изучите последовательность цифр и заполните пробелы
Но наша история на самом деле про то, как фразы вроде «математическая задачка всколыхнула интернет» стали скучными и предсказуемыми попытками привлечь посетителей на страницу. Поскольку даже краткий взгляд на этот вопрос, который впервые появился на техническом форуме Сингапура, позволяет сказать, что это фото – очевидная подделка. Фотография выглядит отредактированной, а к задаче нет пояснений.
Судя по всему, задачку взяли (и видоизменили) с сайта, посвящённого математическим головоломкам, который ведёт Гордон Бёрджин, американский учитель на пенсии. И в варианте с сайта в левой нижней четверти стоит цифра 20. В сингапурской фотке 0 замазан. Неудивительно, что там нет очевидного решения!
«Я поражён этой подделкой и не знаю, чего они пытались этим достичь, – говорит Бёрджин. – Если их целью было бурное обсуждение и последующее отчаяние, то они своего добились!»
Далее идёт правильный вариант загадки.
1. В каждом из четырёх секторов внешнего круга находится двузначное число, равное сумме трёх чисел, расположенных в углах этого сектора. Числа в отдельных кружках могут меняться от 1 до 9, и каждое из чисел может быть использовано только один раз. Одно из чисел дано вам для того, чтобы начать. Найдите оставшиеся четыре.
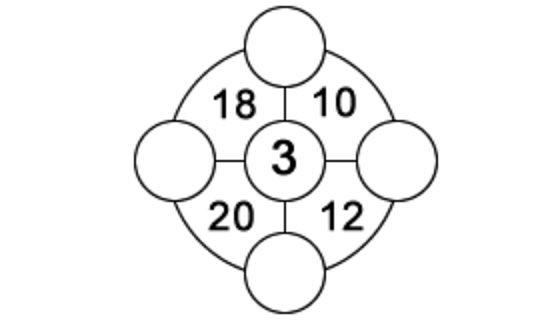
2. Поскольку сингапурская загадка была неправильная – попробуйте предложить вариант задачи, который бы подошёл для приведённой картинки (с затёртым нулём).
Эта загадка напомнила мне задачку из одной из самых интересных книг по истории загадок: "Wakoku chiekurabe", старейшую японскую книгу загадок, опубликованную в 1727 году. Это прекрасная загадка – и, по меньшей мере, она-то как раз родилась на Востоке!
3. Запишите числа от 1 до 9 в чёрных кружочках так, чтобы сумма чисел, находящихся на каждом из двух голубых кругов (включая центральный кружок), а также вдоль горизонтальных и вертикальных линий была одинаковой.
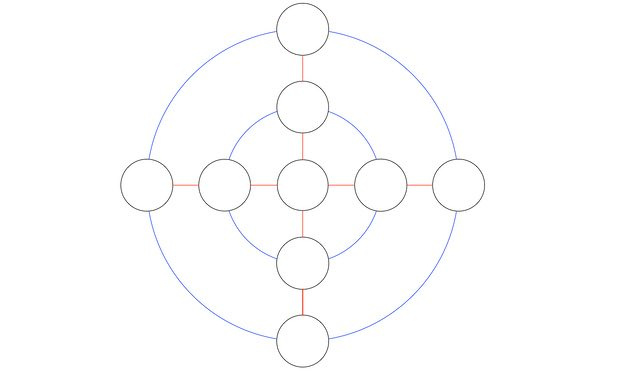
Это четыре суммы, каждая из которых состоит из пяти слагаемых, и все суммы получаются одинаковыми. Вот картинка из самой книги, на которой изображена схожая задача.

Решения

1. По часовой стрелке, начиная сверху: 6, 1, 8, 9
Если мы назовём позиции для чисел Север, Восток, Запад, и Юг, то кандидатами для Запада и Юга будут 8 и 9, поскольку Ю + З + 3 = 20, или Ю + З = 17. Но нам известно, что Ю + В + 3 = 12, или Ю + В = 9. Но Ю не может быть 9, поскольку тогда В = 0, а это запрещено. Поэтому Ю = 8, З = 9, С = 6 и В = 1.
2. Мне больше всего понравилось задание, присланное читателем по имени Том Флэннери, поскольку оно оказалось очень простым.
Заполните круги целыми числами так, чтобы сумма секторов в каждом из полукружий равнялась сумме чисел в кружочках.
3. И последняя задача, из японского сборника загадок 1727 года.
Решений может быть много. Вот моё решение:
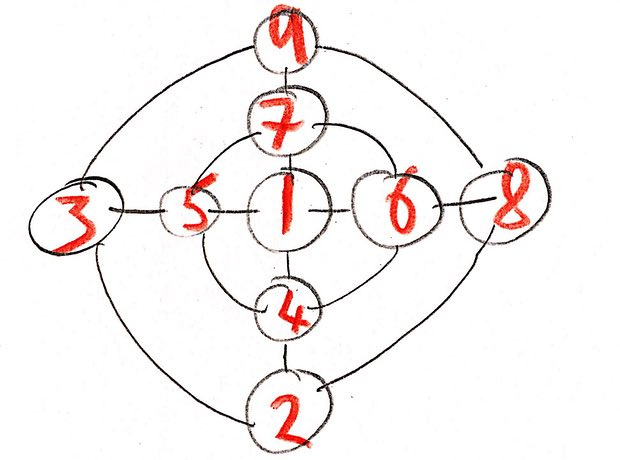
Путь к решению помогает проложить догадка – в центре может быть только нечётное число. Выбрав такое число, нужно разделить оставшиеся цифры на пары, которые в сумме дают одно и то же число, и расположить их в противоположных кружочках. Я выбрал 1 для центра, соответственно остаются пары 2 и 9, 3 и 8, 4 и 7, 5 и 6 – все они дают в сумме 11.











