Привет!
Понадобились мне как-то тензоры (расширения матриц) для моего проектика. Погуглил, нашел целый ряд всяких библиотек, все вокруг да около, а чего нужно — нет. Пришлось реализовать пятидневку и имплементировать то, что надо. Короткая заметка о работе с тензорами и трюках оптимизации.

Итак, что же нам нужно?
Элементы будут храниться в одномерном массиве. Чтобы из набора индексов получить элемент, мы будем умножать индексы на определенные коэффициенты и складывать. А именно, положим, у нас есть тензор [3 x 4 x 5]. Тогда нам нужно сформировать массив из трех элементов — блоков (сам название придумал). Тогда последний элемент равен 1, предпоследний равен 5, а первый элемент — 5 * 4 = 20. То есть blocks = [20, 5, 1]. Например, при обращении по индексу [1, 0, 4] индекс в массиве будет выглядеть как 20 * 1 + 5 * 0 + 4 * 1 = 24. Пока все ясно
… то есть изменение порядка осей. Тупой и простой способ — создать новый массив и загнать туда элементы в новом порядке. Но часто бывает удобно транспонировать, работать с нужным порядком осей, а затем менять порядок осей обратно. Конечно, в этом случае нельзя менять сам линейный массив (ЛМ), а при обращении к определенным индексам, мы будем просто подменять порядок.
Рассмотрим функцию:
Как видим, если поменять blocks местами, то создастся видимость свапнутых осей. Поэтому так и запишем:
Просто меняем номера и длины осей местами.
Подтензор N-мерного тензора это M-мерный тензор (M < N), который является частью исходного. Например, нулевой элемент тензора формы [2 x 3 x 4] это тензор формы [3 x 4]. Его мы получим просто сдвигом.
Представим, что мы получаем подтензор по индексу n. Тогда его первый элемент это n * blocks[0] + 0 * blocks[1] + 0 * blocks[2] + .... То есть сдвиг равен n * blocks[0]. Соответственно, не копируя исходный тензор, мы запоминаем сдвиг, создаем новый тензор со ссылкой на наши данные, но уже со сдвигом. А еще нужно будет выкинуть элемент из blocks, а именно элемент blocks[0], ведь это первая ось, к ней обращений не будет.
Все остальные уже следуют из этих.
Все операции с композицией, которые я определил, можно найти здесь.
Тут уже все просто.
1) Поточечные операции (то есть для двух тензоров операции производятся над парой соответствующих элементов (то есть с одинаковыми координатами)). Реализация тут (объяснение почему такой некрасивый код ниже).
2) Операции над матрицами. Произведение, инверсия, и другие простые операции, мне кажется, объяснения не требуют. Хотя есть что рассказать о детерминанте.
3) Операции над веторами (dot и cross product).
В C# нет темплейтов. Поэтому приходится использовать костыли. Некоторые люди придумали динамическую компиляцию в делегат, например так у него реализована сумма двух типов.
Однако хотелось кастома, поэтому я завел интерфейс, от которого пользователю нужно унаследовать структуру. При этом в самом линейном массиве хранится примитив, а функции сложения, разности, и другие вызываются как
Что инлайнится до вашего метода. Пример имплементации такой структуры.
Далее, хотя кажется, что логично в индексаторе использовать params, то есть как-то так:
На самом деле при каждом обращении будет создаваться массив, поэтому приходится создавать множество перегрузок. Аналогично происходит с другими функциями, работающими с индексами.
Еще я загнал все исключения и проверки в блок #if ALLOW_EXCEPTIONS на случай, если точно нужно быстро, а проблем с индексами точно нет. Небольшой прирост по производительности есть.
На самом деле это не просто так микрооптимизация, которая много чего будет стоить в плане безопасности. Например, в ваш тензор идет запрос, в котором вы и так уже по своим соображениям сделали проверку на корректность данных. Тогда зачем вам еще одна проверка? А они не бесплатные, особенно, если мы экономим даже лишние арифметические операции с целыми числами.
Спасибо Билли, это оказалось очень просто и реализуется через Parallel.For.
Хотя многопоточность это не панацея, и включать ее надо аккуратно. Я провел бенчмарк для поточечного сложения тензоров на i7-7700HQ:
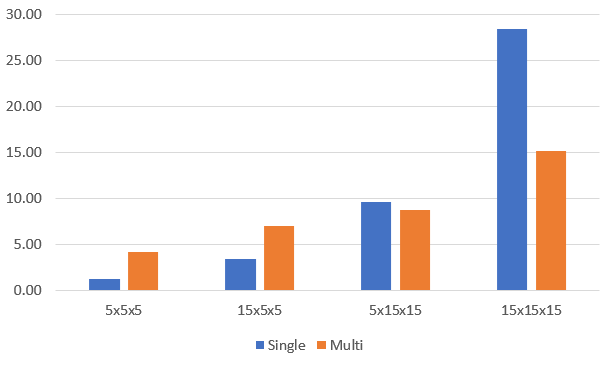
Где Y-ось показывает время (в микросекундах) на выполнение одной операции с двумя целочисленными тензорами определенного размера (размер по оси X).
То есть есть определенный порог, начиная с которого многопоток имеет смысл. Чтобы не надо было думать, сделал флажок Threading.Auto и тупо захардкодил константы, начиная с объема равного которым можно включать многопоток (есть более умный автоматический метод?).
При этом библиотека все равно никак не быстрее игровых матриц, или тем более тех, что подсчитываются на CUDA. А зачем? Те уже написаны, а у нас главное — кастомный тип.
Вот такая коротенькая заметка, спасибо за прочтение. Ссылка на гитхаб проекта здесь. А главный его пользователь — библиотека символической алгебры AngouriMath.
Понадобились мне как-то тензоры (расширения матриц) для моего проектика. Погуглил, нашел целый ряд всяких библиотек, все вокруг да около, а чего нужно — нет. Пришлось реализовать пятидневку и имплементировать то, что надо. Короткая заметка о работе с тензорами и трюках оптимизации.

Итак, что же нам нужно?
- N-мерные матрицы (тензоры)
- Имплементация базового набора методов работы с тензором как со структурой данных
- Имплементация базового набора математических функций (для матриц и векторов)
- Типы Generic, то есть любые. И кастомные операторы
А что уже написано до нас?
Так, в Towel имплементированы матрицы, но есть несколько существенных недостатков:
System.Numerics.Tensor скажете вы. Жаль, у этого типа очень мало методов определено, а главное, он не поддерживает кастомные типы. И, похоже, их подвела собственная технология.
Конечно еще есть всякие MathSharp, NumSharp, Torch.Net, TensorFlow, но это все игровые/ML-овские, ни о каких кастомных типах речи нет.
- Не тензоры, а только матрицы
- Transpose — это «активная» операция, работающая за O(V), где V — объем «фигуры». То есть поменять местами оси вам будет стоить перемещения элементов по всей матрице
В принципе библиотека будет работать с любыми типами, но при работе с ними она будет обращаться в том числе к их операторам. Поэтому если вам вдруг понадобилась работа с типом, у которого нет операторов, придется писать собственную обертку, которая явно не бесплатная по времени.На самом деле можно перезаписывать вызываемые делегаты вручную, хотя это и неочевидно (и еще не так быстро, об этом ниже)
System.Numerics.Tensor скажете вы. Жаль, у этого типа очень мало методов определено, а главное, он не поддерживает кастомные типы. И, похоже, их подвела собственная технология.
Конечно еще есть всякие MathSharp, NumSharp, Torch.Net, TensorFlow, но это все игровые/ML-овские, ни о каких кастомных типах речи нет.
Хранение элементов, транспонирование, подтензор
Элементы будут храниться в одномерном массиве. Чтобы из набора индексов получить элемент, мы будем умножать индексы на определенные коэффициенты и складывать. А именно, положим, у нас есть тензор [3 x 4 x 5]. Тогда нам нужно сформировать массив из трех элементов — блоков (сам название придумал). Тогда последний элемент равен 1, предпоследний равен 5, а первый элемент — 5 * 4 = 20. То есть blocks = [20, 5, 1]. Например, при обращении по индексу [1, 0, 4] индекс в массиве будет выглядеть как 20 * 1 + 5 * 0 + 4 * 1 = 24. Пока все ясно
Транспонирование
… то есть изменение порядка осей. Тупой и простой способ — создать новый массив и загнать туда элементы в новом порядке. Но часто бывает удобно транспонировать, работать с нужным порядком осей, а затем менять порядок осей обратно. Конечно, в этом случае нельзя менять сам линейный массив (ЛМ), а при обращении к определенным индексам, мы будем просто подменять порядок.
Рассмотрим функцию:
private int GetFlattenedIndexSilent(int[] indices)
{
var res = 0;
for (int i = 0; i < indices.Length; i++)
res += indices[i] * blocks[i];
return res + LinOffset;
}
Как видим, если поменять blocks местами, то создастся видимость свапнутых осей. Поэтому так и запишем:
public void Transpose(int axis1, int axis2)
{
(blocks[axis1], blocks[axis2]) = (blocks[axis2], blocks[axis1]);
(Shape[axis1], Shape[axis2]) = (Shape[axis2], Shape[axis1]);
}
Просто меняем номера и длины осей местами.
Подтензор
Подтензор N-мерного тензора это M-мерный тензор (M < N), который является частью исходного. Например, нулевой элемент тензора формы [2 x 3 x 4] это тензор формы [3 x 4]. Его мы получим просто сдвигом.
Представим, что мы получаем подтензор по индексу n. Тогда его первый элемент это n * blocks[0] + 0 * blocks[1] + 0 * blocks[2] + .... То есть сдвиг равен n * blocks[0]. Соответственно, не копируя исходный тензор, мы запоминаем сдвиг, создаем новый тензор со ссылкой на наши данные, но уже со сдвигом. А еще нужно будет выкинуть элемент из blocks, а именно элемент blocks[0], ведь это первая ось, к ней обращений не будет.
Другие операции с композицией
Все остальные уже следуют из этих.
- SetSubtensor форвардит элементы в нужный подтензор
- Concat создает новый тензор, и туда форвардит элементы из двух (при этом длина первой оси — сумма длин осей двух тензоров)
- Stack группирует некоторое число тензоров в один с дополнительной осью (например, stack([3 x 4], [3 x 4]) -> [2 x 3 x 4])
- Slice возвращает Stack от определенных подтензоров
Все операции с композицией, которые я определил, можно найти здесь.
Математические операции
Тут уже все просто.
1) Поточечные операции (то есть для двух тензоров операции производятся над парой соответствующих элементов (то есть с одинаковыми координатами)). Реализация тут (объяснение почему такой некрасивый код ниже).
2) Операции над матрицами. Произведение, инверсия, и другие простые операции, мне кажется, объяснения не требуют. Хотя есть что рассказать о детерминанте.
Сказ о детерминанте
Дело в том, что способов посчитать детерминант не один. Есть классический способ — метод Лапласа, рекурсивный, работает за O(N!). При работе с матрицами больше 3x3 метод Лапласа начинает проигрывать методу Гаусса (приведение матрицы к треугольной и перемножение элементов диагонали).
Но у метода Гаусса есть недостаток для нас, программистов. Для разных типов данных он выразится по-разному: для float это будет существенная потеря точности, а для int это будет просто неверный ответ.
Реализации в интернете отличаются друг от друга, одни требуют модуль числа, а другие используют деление. Мы же почти избежим и того, и другого.
Чтобы избежать ошибок деления, мы заведем тип дробь. Так, любые арифметические операции, включая деление, будут работать с дробью, а в конце функции мы в итоге поделим числитель на знаменатель. Реализацию можно найти тут. SafeDivisionWrapper это как раз та самая дробь.
Хотя у этого метода тоже есть недостаток: переполнение. Ведь если скапливать в числителе и знаменателе параллельно, то вместо одного небольшого числа у нас получится дробь с огромными знаменателем и числителем. Поэтому я оставил и не SafeDivision версию (для типов с большой точностью, или нечисленных типов его хватит).
Но у метода Гаусса есть недостаток для нас, программистов. Для разных типов данных он выразится по-разному: для float это будет существенная потеря точности, а для int это будет просто неверный ответ.
Реализации в интернете отличаются друг от друга, одни требуют модуль числа, а другие используют деление. Мы же почти избежим и того, и другого.
Чтобы избежать ошибок деления, мы заведем тип дробь. Так, любые арифметические операции, включая деление, будут работать с дробью, а в конце функции мы в итоге поделим числитель на знаменатель. Реализацию можно найти тут. SafeDivisionWrapper это как раз та самая дробь.
Хотя у этого метода тоже есть недостаток: переполнение. Ведь если скапливать в числителе и знаменателе параллельно, то вместо одного небольшого числа у нас получится дробь с огромными знаменателем и числителем. Поэтому я оставил и не SafeDivision версию (для типов с большой точностью, или нечисленных типов его хватит).
3) Операции над веторами (dot и cross product).
Оптимизация
Темплейты?
В C# нет темплейтов. Поэтому приходится использовать костыли. Некоторые люди придумали динамическую компиляцию в делегат, например так у него реализована сумма двух типов.
Однако хотелось кастома, поэтому я завел интерфейс, от которого пользователю нужно унаследовать структуру. При этом в самом линейном массиве хранится примитив, а функции сложения, разности, и другие вызываются как
var c = default(TWrapper).Addition(a, b);
Что инлайнится до вашего метода. Пример имплементации такой структуры.
Индексация
Далее, хотя кажется, что логично в индексаторе использовать params, то есть как-то так:
public T this[params int[] indices]
На самом деле при каждом обращении будет создаваться массив, поэтому приходится создавать множество перегрузок. Аналогично происходит с другими функциями, работающими с индексами.
Исключения
Еще я загнал все исключения и проверки в блок #if ALLOW_EXCEPTIONS на случай, если точно нужно быстро, а проблем с индексами точно нет. Небольшой прирост по производительности есть.
На самом деле это не просто так микрооптимизация, которая много чего будет стоить в плане безопасности. Например, в ваш тензор идет запрос, в котором вы и так уже по своим соображениям сделали проверку на корректность данных. Тогда зачем вам еще одна проверка? А они не бесплатные, особенно, если мы экономим даже лишние арифметические операции с целыми числами.
Многопоточность
Спасибо Билли, это оказалось очень просто и реализуется через Parallel.For.
Хотя многопоточность это не панацея, и включать ее надо аккуратно. Я провел бенчмарк для поточечного сложения тензоров на i7-7700HQ:

Где Y-ось показывает время (в микросекундах) на выполнение одной операции с двумя целочисленными тензорами определенного размера (размер по оси X).
То есть есть определенный порог, начиная с которого многопоток имеет смысл. Чтобы не надо было думать, сделал флажок Threading.Auto и тупо захардкодил константы, начиная с объема равного которым можно включать многопоток (есть более умный автоматический метод?).
При этом библиотека все равно никак не быстрее игровых матриц, или тем более тех, что подсчитываются на CUDA. А зачем? Те уже написаны, а у нас главное — кастомный тип.
Вот так вот
Вот такая коротенькая заметка, спасибо за прочтение. Ссылка на гитхаб проекта здесь. А главный его пользователь — библиотека символической алгебры AngouriMath.
Немного про наши тензоры в AngouriMath
Для нее эти тензоры полезны нечисленностью, ведь в AM-е тип элемента это Entity, кастомный класс. К примеру,
Вернет в ответ
var t = MathS.Matrices.Matrix(3, 3,
"A", "B", "C", // Эти буквы парсятся как символьные переменные, тут могло быть и "A * 3", и "sqrt(sin(x) + 5)"
"D", "E", "F",
"G", "H", "J");
Console.WriteLine(t.Determinant().Simplify());
Вернет в ответ
A * (E * J - F * H) + C * (D * H - E * G) - B * (D * J - F * G)








