
Комментарии 15
А для чего нужно строить обратные ребра? Может, какой-то пример, где они пригождаются?
Если меня не глючит, то даже в этом графе, если порядок нахождения путей будет другой, обратные ребра будут задействованы. А нужны они на случай, если найденный путь нагрузит одно из ребер больше, чем оптимальное распределение, в этом случае в графе появится путь через обратное ребро, разгружающий его таким образом, при этом поток из истока будет увеличиваться. Без обратного ребра найденное решение было бы неоптимальным.
Пример: граф в форме ромба с одной диагональю, А-исток, Д-сток, ВС-ребро в середине, АВ=7, ВС=4, СД=5, АС=3, ВД=4. Предположим, первым найден путь АВСД, вычитаем максимум (4), остаточная сеть остается АВ=3, ВС=0, СД=1, СВ=4 (обратное ребро). Дальше находим пути АВД и АСД, остается сеть АВ=0, ВД=1, АС=2, СД=0, и при отсутствии обратного ребра СВ решение неоптимально из-за перегрузки пути АВСД. Но оно есть и мы находим ещё один путь АСВД на 1 и получаем ответ 4+3+1+1=9.
Этот алгоритм применяют например при расчете транспортных потоков в городе
Интересно!
Но... Хотелось бы увидеть программную реализацию алгоритма.
Я долго думал над этим, а именно стоит ли добавлять реализацию!?
Но потом решил, что не стоит, ибо идея самой статьи - изложить саму сущность алгоритма на очень примитивном уровне. С минимальным уровнем математики и формального языка.
Если хотите углубиться в алгоритм, то можете посмотреть лекцию Павла Маврина на ютубе по этой теме. Всего хорошего! :)
я в давние времена реализовывал как практическую часть к лабораторной в универе — https://github.com/platinumthinker/ford_falkerson_flow
Объясните, пожалуйста, откуда взялись цифры на рёбрах на рисунке "Начальная остаточная сеть"? С виду как будто не имеют никакого отношения к рисунку из "Постановки задачи".
Попробую объяснить.
По исходному графу строим производный граф, который и будем называть остаточной сетью.
Остаточная сеть, в отличие от исходного, может иметь обратные ребра. Проще говоря, ребра, по котором можно вернуть жидкость, которую вы отправили из одной точки в другую. То есть, вы не только можете отправлять жидкость из одной точки в другую, но и можете, при необходимости, вернуть.
Советую почитать комментарий сверху, где коллега рассказал про то, для чего нужны обратные ребра.
Так вас же спрашивают, почему графы на рисунках «Постановка задачи» и «Начальная остаточная сеть» разные, когда вроде бы должны быть одинаковые. У них мало того, что веса рёбер отличаются, так ещё и ребро CB во втором графе развёрнуто в обратную сторону (то есть, это вообще другой граф).
Если бы не направленность графа, выглядело бы как типовая задача расчёта тока в ТОЭ.
github.com/Malkovsky/interactive-visualization/blob/master/examples/ford-fulkerson.ipynb
Если хочется посмотреть и потыкать, но не хочется мучаться с установкой, можно онлайн в биндере (в репе есть ссылка), но возможно придется подождать сборку докер-образа
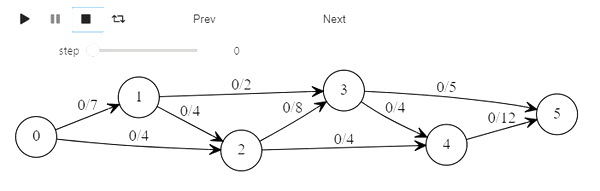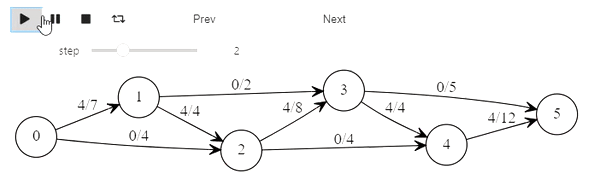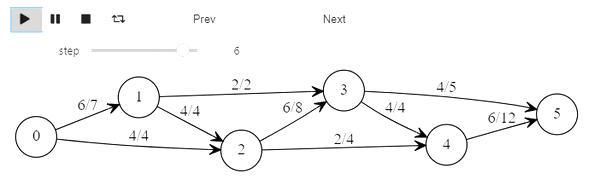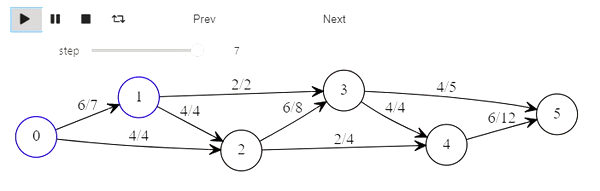
Алгоритм Форда-Фалкерсона