
Комментарии 8
А почему не рассказали, как числа Фибоначчи и функция Эйлера используются в комбинаторике?
Автору, спасибо за материал, математика интересная наука.
Если сказать честно, я знаю не слишком много об этих числах.
Так технические статьи не выкладывают, сначала надо разобраться а потом публиковать, а не наоборот :) Простой поиск в гугле уже даст кучу ссылок. Про числа Фибоначчи вообще можно много чего написать, например про их «нахождение» в природе: https://stemettes.org/zine/articles/fibonacci-in-nature/
Из описания функции Эйлера в тексте не ясно, для чего она нужна и в чем практический смысл.
Еще можно добавить код на Python или другом языке, чтобы читатели могли сами с комбинаторикой поэкспериментировать.
Удачи.
Также хочу отметить, что если число можно представить и как степень и как два множителя, то в преимуществе всегда степень какого-то числа (о как, в рифму).
Способ 3 функции Эйлера работает только для взаимно простых множителей.
Автор молодец, но: 1)Довольно поверхностно, для числа сочетаний можно было написать как выводится формула. 2)Для чисел Фибоначчи можнл было вывести формулу и рассказать про числа каталана. 3) в функции Эйлера опять все поверхностно, и разбор лучше делать не на конкретных примерах вроде 6=2*3, а для k=n*m
Вообще такие вещи в хороших школах на матане изучаются. В моей 57 тоже :)
Спасибо большое! Хорошо и доступно написано
Коллеги, спасибо за комментарии. Я эту статью написал в 2015 году, мне тогда действительно было 14 лет. Удивлён, что спустя больше 6 лет ее решили опубликовать из песочницы...
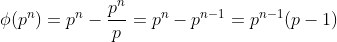
Интересное и простое из комбинаторики. Функция Эйлера