То что общество делиться на социальные классы - ни для кого не секрет. Во все времена людям было интересно узнать, почему они находятся не там где им хотелось бы и пытались найти этому объяснение. В средние века, все объяснялось Божьей Волей, и, по-видимому, большинство такое объяснение устраивало, ведь перейти из одного социального класса в другой было крайне затруднительно (а в индуизме, с его кастовой системой, едва ли возможно).
В новое время ситуация сильно изменилась, поскольку капитализм (а затем и социализм) предложили социальный лифт, который позволил многим людям повысить свой социальный статус и материальное положение. Многим, но не всем... И вот уже в наше время, появились всякие там курсы личностного и профессионального роста, где коучеры, во что бы то ни стало, утверждают что успеху можно научить (заплатив им, разумеется, определенную сумму). На самом деле польза таких тренингов очень спорна, и в этой статье мы не будем касаться этой темы. Более того, вряд ли она может считаться научной... Заметим, что наука тоже пытается ответить на вопрос, почему одни люди успешные, а другие не очень. Обычно делается это при помощи оценки человеческого интеллекта, оставляя за скобками другие, не менее важные (а порой и много более важные) факторы. Такие, как изначальное социальное (материальное) положение, связи и другие человеческие качества и таланты, напрямую не связанные с интеллектом. К тому же интеллект - тоже очень относительное понятие, и в наши дни, кроме "классического" определения интеллекта - IQ, все чаще говорят о так называемом, эмоциональном интеллекте, который по мнению многих коучеров и менеджеров, есть более важный фактор в достижении успеха (по сравнению с обычным IQ). Кроме того, говорят еще о политическом, социальном, духовном (и.т.д, смотри Рис. 1) интеллекте...
Только не совсем ясно, как, например, можно измерить духовный интеллект!.. В отличие от экзотических определений, классический IQ может быть измерен при помощи довольно простого теста, и кроме того, статистическое распределение этого показателя (в различных человеческих группах), хорошо исследовано. Поэтому, классический IQ предоставляет хорошую возможность проводить социологические исследования и строить статистические модели, которые, например, оценивают корреляцию между IQ и другими социальными показателями. Данная статья предлагает математическую модель, с помощью которой попробуем оценить влияние IQ на переход индивида из одного социального класса в другой. Заметим, что модель статистическая, и IQ определяет лишь шанс на успех. Другими словами, факторы не связанные с IQ (и просто обычная удача), в нашей моделе "схвачены" случайностью и, как и во многих других исследованиях модель позволяет лишь судить о корреляции между IQ и успехом, но никак не больше.
Тесты IQ разрабатываются так, чтобы результаты описывались нормальным распределением с медианным значением IQ, μ=100 и стандартным отклонением σ=15 (https://en.wikipedia.org/wiki/Intelligence_quotient). Для того чтобы связать уровень интеллекта с успехом (перехода в более высокий социальный класс), определим при помощи рекурсии следующую функцию, которую обозначим как CS (Chanse for Success):
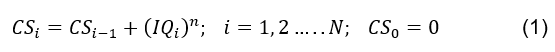
В уравнении (1), CSi, определяет шанс на успех у индивида i, чей уровень интеллекта равен IQi. Для наглядности, на Рис. 2(a), функция CS представлена в графическом виде, при n=1, в случае популяции состоящей всего из пяти индивидов, чей IQ равен 100, 90, 120, 80, 110. Очевидно, что "площадь" занимаемая каждым индивидом пропорциональна его IQ (в случае n=1). Теперь используя непрерывное равномерное распределение, выбираем "счастливого" индивида, которого переводим в следующий социальный класс. Таким образом более низкий социальный класс теряет одного индивида, в то время как следующий социальный класс пополняется новым индивидом. Непрерывное равномерное распределение, F(x), в нашей моделе, определяется как:
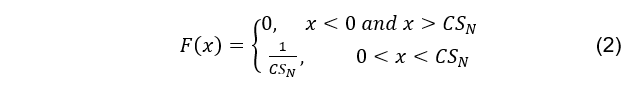
В результате используя распределение F(x), получаем что действительно, шанс индивида "быть избранным", пропорционален его IQ. Пропорционален, в случае n=1 и, для того чтобы усилить влияние интеллекта на счастливый исход, можно изменить степень n в уравнении (1), с единицы на более высокое значение. Тогда шанс на успех будет пропорционален не IQ, а (IQ)n. При n=3, функция CS показана на Рис. 2(b), и сравнивая "площади" занимаемые каждым индивидом (снова, в случае IQ=100, 90, 120, 80, 110), легко заметить, что в данном случае интеллект играет более значительную роль.

Очевидно, что при n→∞, модель становится детерминистской, поскольку исход предопределен: индивид с максимальным значением IQ (он, и только он) будет переведен в следующий социальный класс. С другой стороны, если n=0, то IQ не играет никакой роли, и успех определяется чистой случайностью.
Операция выбора индивидов "на повышение" повторяется столько раз, сколько индивидов должно быть в следующем социальном классе. После того как новый класс сформирован, из него, в свою очередь, можно создать ещё более высокий социальный класс, повторяя тот же самый цикл выбора. Важно отметить, что предлагаемая модель основана на следующих предположениях:
Индивид может перейти в следующий социальный класс, поднимаясь только на одну ступеньку вверх, и не может "перепрыгнуть" через ступеньку.
Возможность спуститься в более низкий социальный класс не предусмотрена моделью. Полагаем, что индивид потерявший работу (потерпевший неудачу в бизнесе, и.т.д.), может довольно быстро восстановить свое социальное положение. Опять же, насколько данное предположение верно - вне рамках данной статьи.
Изначально (скажем, по окончанию средней школы), все индивиды находятся внизу социальной пирамиды. Неравные начальные условия, богатые наследники, и.т.д - вне нашей модели.
Общее количество индивидов в популяции неизменно. Рождение новых индивидов и смерть, в модель не включаются.
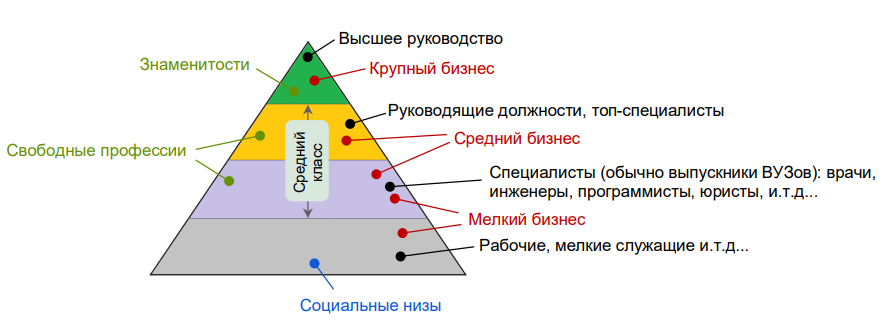
На сколько социальных классов распадается общество - очень спорный вопрос. Все зависит от определения! Условно поделим на четыре класса (прям как четыре касты когда-то в Индии: брахманы, кшатрии, вайшьи и шудры!), и в таком случае социальная пирамида будет выглядеть где-то примерно так, как показано на Рис. 3. Опять же, представленное нами, не может считаться однозначным: возможно кто-то предложит несколько другое определение.

Теперь следующий вопрос: каков процентный состав данной пирамиды? Или какой процент населения в каждом социальном классе?.. Очевидно, что однозначного ответа нет и быть не может. Зависит и от социальной системы, и от экономической ситуации, и от многих других вещей. Тогда просто введем параметр, который определит процентный состав, и параметрически исследуем его влияние. Обозначим этот параметр, как, r (ratio), и при помощи рекурсивного соотношения, определим соотношение между двумя соседними классами, как:
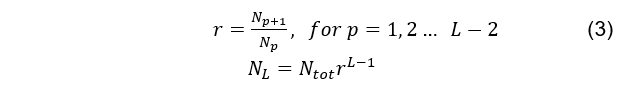
В уравнении (3), L означает количество социальных классов. В соответствии с Рис. 3 и уравнением (3), L=4 (где, 1- низший, а 4-высший класс), а Ntot - общее количество индивидов в социуме. Разумеется, r может быть не постоянным, например: N2/N1 » N3/N2. Причем вряд ли есть основания полагать, что он должен быть постоянным, но на данный момент допустим что это так. Для удобства, рекурсивное уравнение (3) можно привести к явному виду:
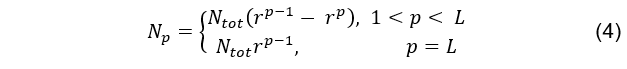
Условимся, что количество людей в социуме, Ntot, составляет 10,000. Тогда в соответствии с параметром r и уравнением (4) получим распределения населения по социальным классам, как показано в таблице 1. При r=0.05, подавляющее количество населения "прозябает" в низшем классе, и только чуть больше чем один индивид (на 10,000!) попадает в самый высокий класс. Другой предельный сценарий - r =0.5: в этом случае, социальный лифт действует очень хорошо, и поэтому только половина населения (самые не успешные) находятся в низшем социальном классе. Заметим, что при значениях r превышающих 0.5, социальная пирамида перестает быть пирамидой, поскольку количество индивидов в высших классах можете превысить их количество в более низких. Например, для r=0.8, в соответствии с уравнением (4), получим вот какое распределение: N1=2,000, N2=1,600, N3=1,280 и N1=5,120 - совсем не пирамида!

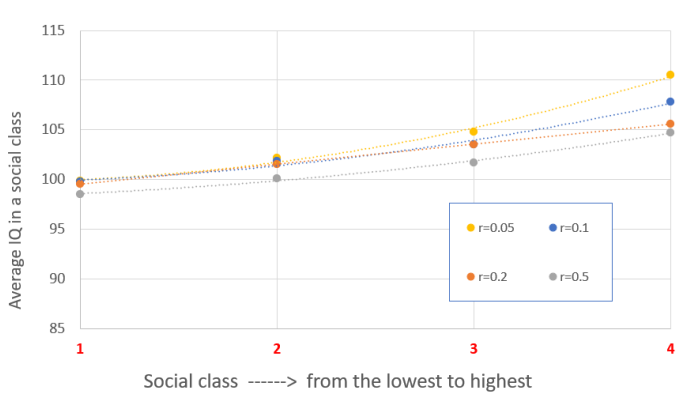
Используем код на MATLAB, для проведения вероятностных симуляций в соответствие с уравнениями (1) и (2). Подсчитываем, среднее значение IQ в каждом из четырех классов, и для получения статистически репрезентативных результатов, проводим симуляцию 20 раз, для каждого значения r в таблице 1. В конечном итоге, чтобы минимизировать статистическую погрешность, оцениваем среднее значение IQ для каждого социального класса, при помощи усреднения результатов 20 симуляций, как приведено в таблице 2. Полученные значения усредненного IQ, показаны на графике (Рис. 4), как функция от номера социального класса (от 1 то 4), для n=1 и r=0.05, 0.1, 0.2 и 0.5 (в соответствии с таблицей 1). Анализируя результаты на графике, нетрудно заметить что градиент кривой (dy/dx, где y - усредненный IQ и x - номер социального класса) усиливаться с уменьшением параметра r. Это вполне ясно: чем меньше индивидов могут находиться в высших классах, тем труднее подняться по социальной лестнице и тем "умнее" должен быть индивид. Несомненно, могут быть исключения, но статистически (на достаточно больших выборках) это так. И наоборот: при более высоких значениях r, происходит как бы инфляция высших классов. При r =0.5, только 50% индивидов находятся в самом низшем социальном классе (таблица 1), и разумеется, что не каждый кто "преуспел" обладает высоким IQ. Следовательно, для r = 0,5 разница между самым высоким и самым низким усредненным IQ, составляет всего около 6 баллов, в то время как для r=0.05, эта разница превышает 10 баллов. Можно предположить, что r = 0.05 подходит для описания общества с очень ограниченными возможностями, а r = 0.5, для общества с хорошим социальным лифтом (скажем, в случае экономического бума).

Влияние параметра n (уравнение 1) на распределение усредненного IQ показано на графике Рис. 5. Для исследования этого параметра, зафиксируем параметр r на значении 0.1, и проделаем те же самые расчеты, как и в предыдущем случае (20 симуляций + усреднение). Результаты на этом графике также вполне интерпретируемы: Чем выше значение степени n, тем большую роль в достижении успеха играет интеллект, и поэтому в высшие классы попадают в основном самые умные индивиды. Если внимательно присмотреться, то можно заметить, что при очень высоких значениях n, (n=5 или 10) индивиды внизу социальной пирамиды в среднем имеют более низкий IQ, чем для случая n=1. Это происходит из-за того, что самые интеллектуальные индивиды имеют хороший шанс подняться по социальной лестнице, и, следовательно, в самом низком классе остаются не самые умные. Легко догадаться, что при значениях n, стремящимся к 0 (параметр n может быть и дробным), IQ будет иметь исчезающе малый эффект на социальный успех (среднее значение IQ во всех классах будет примерно одинаковым); по-видимому такое описание подходит для феодального или сильно коррумпированного общества.
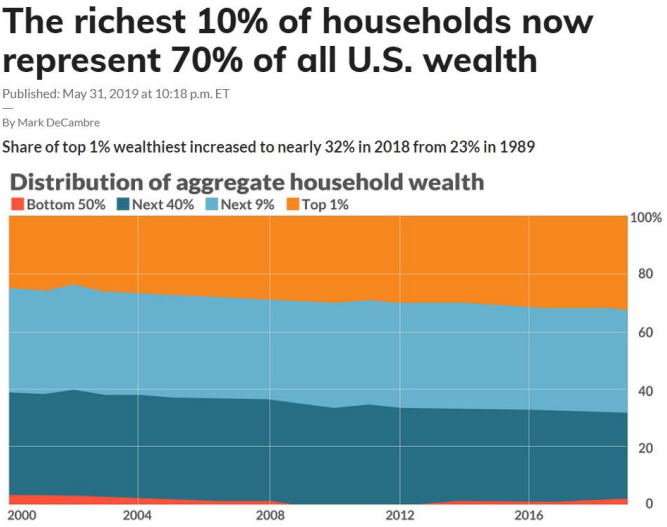
А теперь самый существенный вопрос: насколько предлагаемая модель подходит для описания реального положения вещей в социуме? Вопрос, очевидно, не простой, поскольку исследований и статистических данных в этой области собрано не мало, и зачастую они противоречивы. Тем не менее попробуем экспериментально проверить нашу модель. Сначала надо решить, как разделить социум для численных экспериментов. Каких-то фундаментальных законов тут нет, и конечно-же в интернете можно найти все что угодно. Тем не менее выберем классификацию, приведенную для домашних хозяйств в США. Диаграмма показана на Рис. 6, где разительный заголовок, сообщает о растущем неравенстве. Но нас интересует лишь процентный состав классов (социальная справедливость и эрозия среднего класса - за пределами данной статьи).
Предположим, что структура социума в соответствии с домохозяйствами, также подходит и для структуры по индивидам. Другими словами, если индивид находится в определенном социальном классе, то и его семья там же. В принципе, разумное предположение. Также заметим, что в соответствии с приведенной диаграммой, мы вынуждены предположить, что финансовое положение определяет и принадлежность к социальному классу. Как и в наших предыдущих расчетах, в соответствии с диаграммой Рис. 6, общество распадается на четыре класса (смотри Рис. 6): низший класс - 50% населения, 40% следующий класс (условно средний класс) и два последних топ-класса - 9% и 1%.

Результаты на графике Рис. 7, соответствуют социальной структуре на Рис. 6 и параметрам n = 1, 2 и 5. Пожалуй, ничего особенного - очень напоминает предыдущие результаты на Рис. 5.

Теперь обратимся к еще одному источнику. Это статья на тему IQ, которая называется "Unmasking the IQ Lie" (https://archive.scienceforthepeople.org/vol-6/v6n2/unmasking-the-iq-lie/). Как и следует из названия статьи, авторы (J. Selcer, S. Conrad, S. Flaschman, A. Weinrub, S. Orbach, J. Schwartz, & M. Schwartz) критически относятся к идее того, что IQ может влиять на успех и карьеру. В своей работе они используют данные довольно известного психолога R. Herrnstein, который как-раз то и утверждал, что IQ есть очень важный фактор успеха. Не касаясь социальных и политических взглядов различных исследователей, мы просто воспользуемся таблицами в статье. Вот какие данные приведены в таблице 3. Вся популяция (всего 100 опрашиваемых) делится на 10 групп по экономическому успеху (группа-1 → 10% с самым низким доходом и группа-10 → 10% с самым высоким доходом), и по IQ (группа-1 → 10% с самым низким IQ и группа-10 → 10% с самым высоким IQ). Каждое число в матрице (таблице) находится на пересечении определенной экономической (по вертикали) и интеллектуальной (по горизонтали) группы. Число означает процент тех кто находится одновременно в этой же экономической группе и в группе по IQ. Поясним на примере. Возьмем для этого, самую высокую экономическую группу (верхняя строка), и посмотрим на левую (10% самых умных) и правую (10% самых тупых) колонки. Число 30.9 в левой колонке таблицы 3(а), означает, что примерно 31 человек из 100, относящихся к самой успешной экономической группе, также находятся в топ-группе самых умных. И соответственно, число 0.6 в правой колонке, означает что из топ-группы самых экономически успешных, менее одного человека (0.6 из 100) находятся в IQ-группе самых тупых. Есть существенная разница между данными в таблицах 3(а) и 3(b). В первом случае, в опрашиваемую популяцию включаются все индивиды, а во втором - индивиды происходящие из равных социальных слоев (по-видимому “social class background”, можно также понимать как “с равными начальными возможностями”) и с одинаковым уровнем образования.

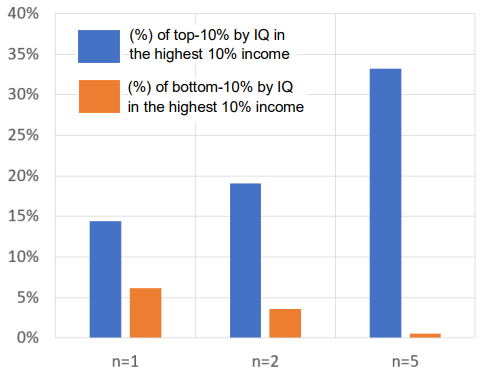
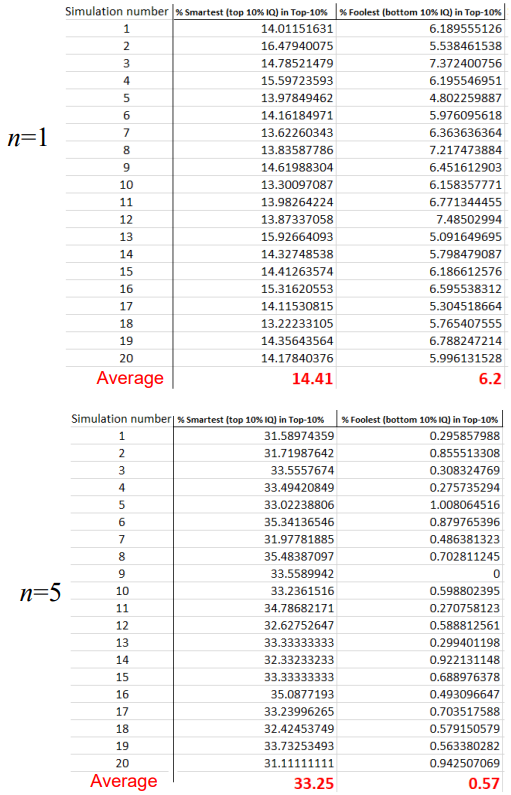
Теперь снова обратимся к нашей моделе, и проверим её предсказательную мощность. Два высших класса на графике Рис. 7 (9% + 1%), как-раз и составляют 10% самых экономически успешных (так был структурирован социум в наших симуляциях, в соответствии с данными на Рис. 6). Осталось лишь подсчитать количество самых умных и самых тупых в этих двух классах (напомним, что в наших симуляциях это 1,000 индивидов), и чтобы найти процентное соотношение, подсчитать так же количество самых умных и самых тупых в общей популяции. Топ-самых умных (10%) это те индивиды чей IQ превышает примерно 119, и соответственно самые тупые (10%) это те, чей IQ ниже 81. Это нетрудно подсчитать интегрируя функцию нормального распределения (Рис. 8). Напомним, что IQ описывается нормальным распределением с медианным значением 100 и стандартным отклонением 15. Результаты наших симуляций для n=1, 2 и 5 показаны на графике Рис. 9. и в таблице 4, для n=1 и 5. Получилось очень неплохое совпадение с результатами таблицы 3! Для n=1 (экономический успех пропорционален IQ), получается что 14.41% самых умных (IQ>119) из всей популяции попадают в самую успешную группу. И только 6.2% самых тупых (IQ<81) из всей популяции попадают в эту группу. Это очень близко к численным значениям в таблице 3(b): 14.1% и 6.6%! Так дела обстоят, для тех чье образование и классовое происхождение на одном уровне (таблица 4(b)). А вот если n=5, то результаты нашей модели хорошо предсказывают данные таблицы 3(а): 33.25% самых умных из всей популяции попадают в самую успешную группу (по таблице 3(а) - 30.9%), и только 6.2% самых тупых (по таблице 3(а) – 0.6%). Примечательно, что согласно нашей модели, процент самых умных (IQ>119) увеличиваться и самых тупых (IQ<81) уменьшается, с увеличением параметра n. Это вполне объяснимо, так-как с увеличением этого параметра, роль интеллекта в успехе становится более значительной, и индивиды с низким IQ едва ли могут попасть в высшие 10%. Почему такая разница между данными в таблице 3(а) и 3(b)? Почему в первом случае наша модель хорошо работает для n=5, а во втором - для n=1? По-видимому из-за того, что данные в таблице 2(b) относятся к индивидам с одинаковым уровнем образования, в то время как образование представляет собой достаточно мощный инструмент для достижения успеха. Но только для индивидов с высоким IQ! Для индивидов с низким IQ образование имеет обратный эффект, так-как им становиться труднее конкурировать с более умными индивидами. Скорее всего, это и объясняет почему для индивидов с разными уровнями образования степень n имеет более высокое значение, чем в случае когда у всех индивидов образование и социальное происхождение на одном уровне.
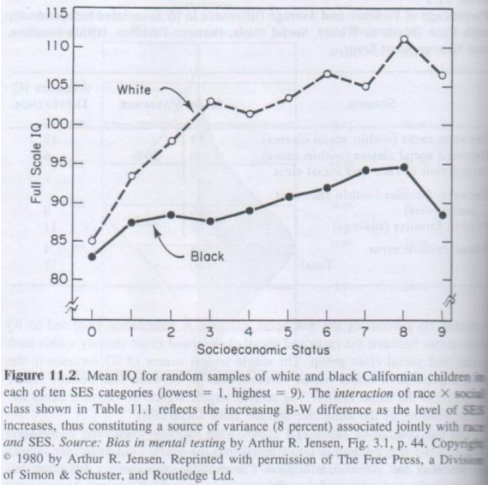
Испытаем нашу модель еще на одном примере. Данные на графике Рис. 10, были собраны в Калифорнии в 1980 году. Кривые на графике представляют IQ у детей белых американцев и у детей афроамериканцев, в зависимости от социально-экономического статуса их семей. Как и в предыдущем примере, все население (точнее, все семьи) поделено на 10 классов в соответствии с социально-экономическим положением. Чтобы использовать эти данные, введем еще одно допущение: предположим, что IQ передается по наследству. Другими словами, мы предполагаем, что значения CH на графике относятся не только к детям, но и к их родителям. Заметим, что до сих пор между учеными нет однозначного мнения о том, насколько велико влияние генетики на IQ. Очевидно одно: оно есть, и исключать генетические факторы при оценке интеллекта никак нельзя. Возможно, что для нашей модели мы допустили слишком сильное влияние генетики, но на то это и допущение.

Чтобы симуляции не были слишком громоздкими, допускаем что вся популяция состоит всего из 1,000 индивидов, и что в каждой группе их 100. Повторяем алгоритм выборки 10 раз в каждой симуляции; для статистической репрезентативности запускаем симуляцию 20 раз и усредняем результат (как и в прошлых примерах). Используя метод наименьших квадратов, пытаемся подобрать такие значения параметра n, чтобы кривые предсказанные моделью совпадали с данными на графике Рис. 10. Наилучшее совпадение получается для n =1 в случае афроамериканцев (m≈89.5) и n=2 для белых американцев (m≈100), как показано на графике Рис. 11. Выходит, что для разных рас значение параметра n (влияние IQ на социоэкономический статус) отличаются. В чем причина такого отличия - не относится к теме данной статьи.
Что можно сказать в заключении? Очевидно, что наша модель не описывает никакой фундаментальный закон, а скорее просто основана на интуиции. Сравнивая модель с экспериментальными данными, было показано, что один из параметров модели (степень n, определяющая влияние IQ на успех), может сильно отличаться от одного социума к другому. Предложенная нами модель достаточно проста и, несомненно, может быть развита в будущем с целью включения дополнительных факторов.
В принципе, могут существовать и другие системы (никак не связанные с IQ или социологией), где предложенная модель может быть применена. Все, что нужно,- это статистическое влияние одного фактора на прогрессивное (поступательное) изменение другого, а таких явлений немало.











