Сезон пожаров
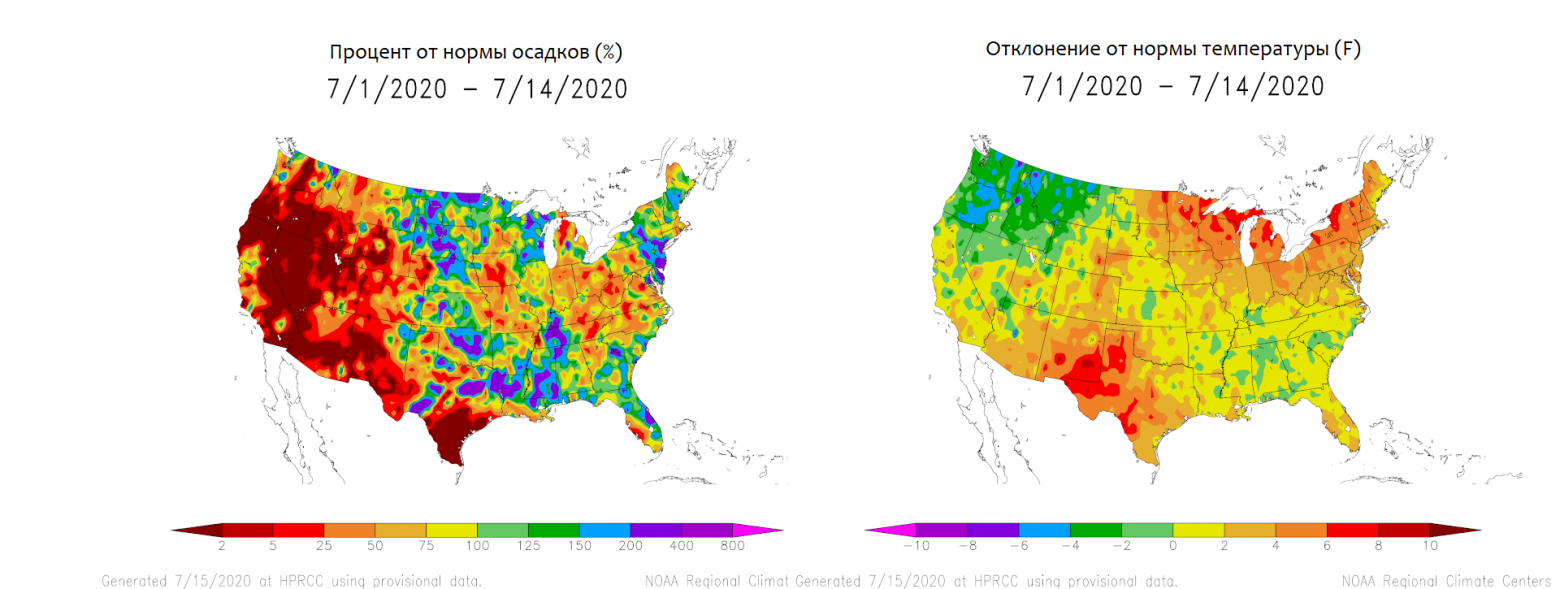
В июле западная часть Соединенных Штатов обычно вступает в самый разгар пожароопасного сезона. Во многих частях страны в это время выпадает меньше среднего количества осадков и температура выше среднего, что создаёт жаркие, сухие условия, идеальные для лесных пожаров.
Математические модели распространения огня являются важной частью борьбы с пожарами. Модели могут помочь определить, где может начаться пожар, как быстро он будет распространяться (и в каком направлении), и сколько тепла он будет выделять; эти важные подсказки могут спасти жизни и существенно сократить финансовые потери.
Принцип Гюйгенса
Некоторые из наиболее широко используемых симуляторов пожара (например, FARSITE, Prometheus) основаны на принципе распространения волн Гюйгенса. Он был первоначально предложен для описания распространения световых волн, а также объясняет, как звуковые волны могут распространяться по углам. Суть принципа Гюйгенса заключается в том, что каждая точка на краю волнового фронта может быть независимым источником вторичных волн, которые распространяют волну.
Хотя Гюйгенс изучал свет (а не звук) и никогда не был женат, я представляю себе именно это:
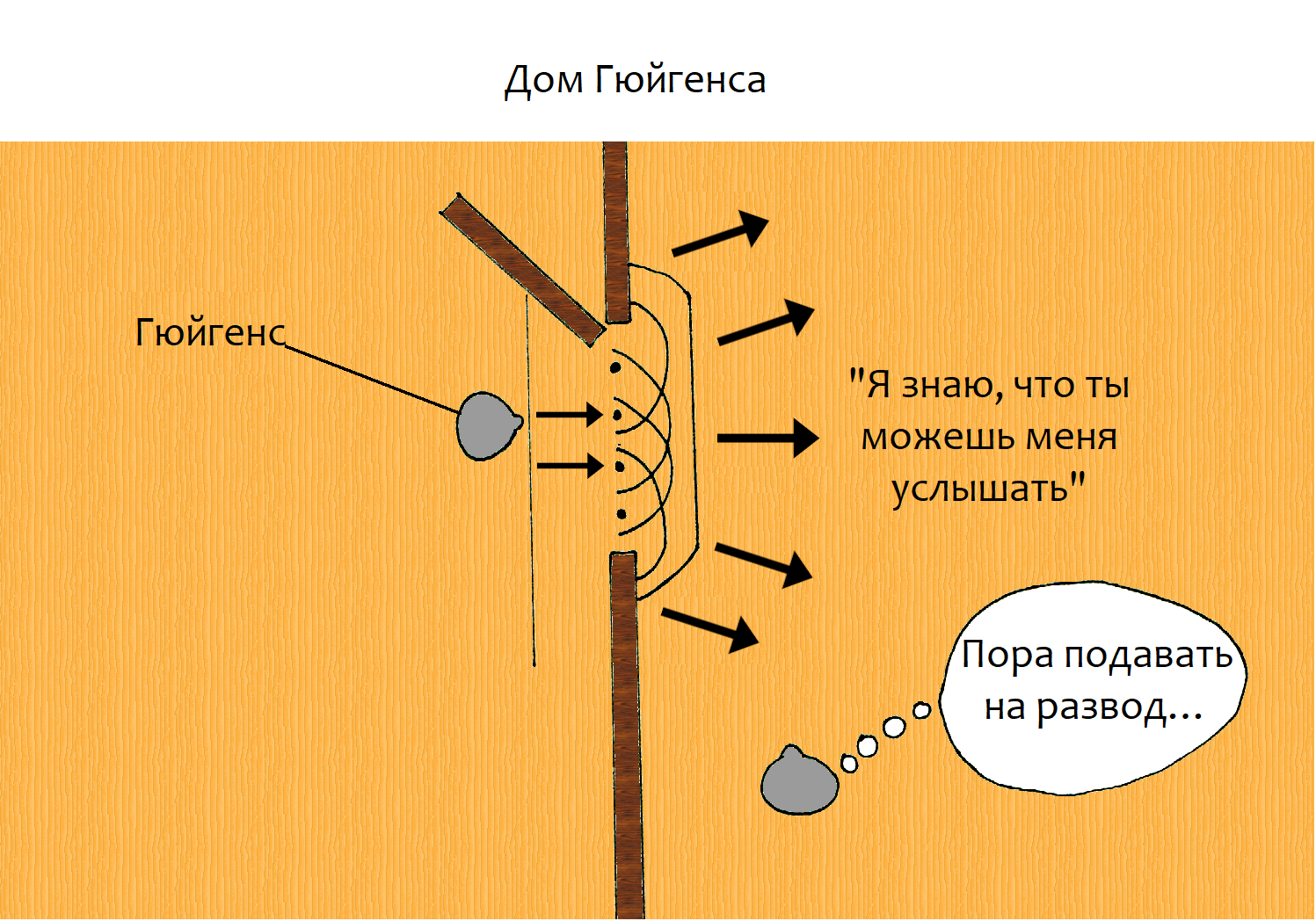
Модели пожаров, включающие принцип Гюйгенса, моделируют распространение огня в виде эллиптической волны, которая распространяется через меньшие вторичные эллиптические волны на фронте пожара. На каждом временном шаге модель использует информацию о пожарной обстановке для определения формы, направления и размера (скорости распространения) каждой вторичной волны. Форма и направление определяются вектором наклона ветра, а размер определяется уровнем горючего материала.
Новый волновой фронт – это поверхность, касательная ко всем вторичным волнам. Другими словами, маленькие эллипсы образуют своего рода оболочку вокруг исходного периметра пожара, а внешний край этой оболочки является новым фронтом пожара.
Клеточные автоматы
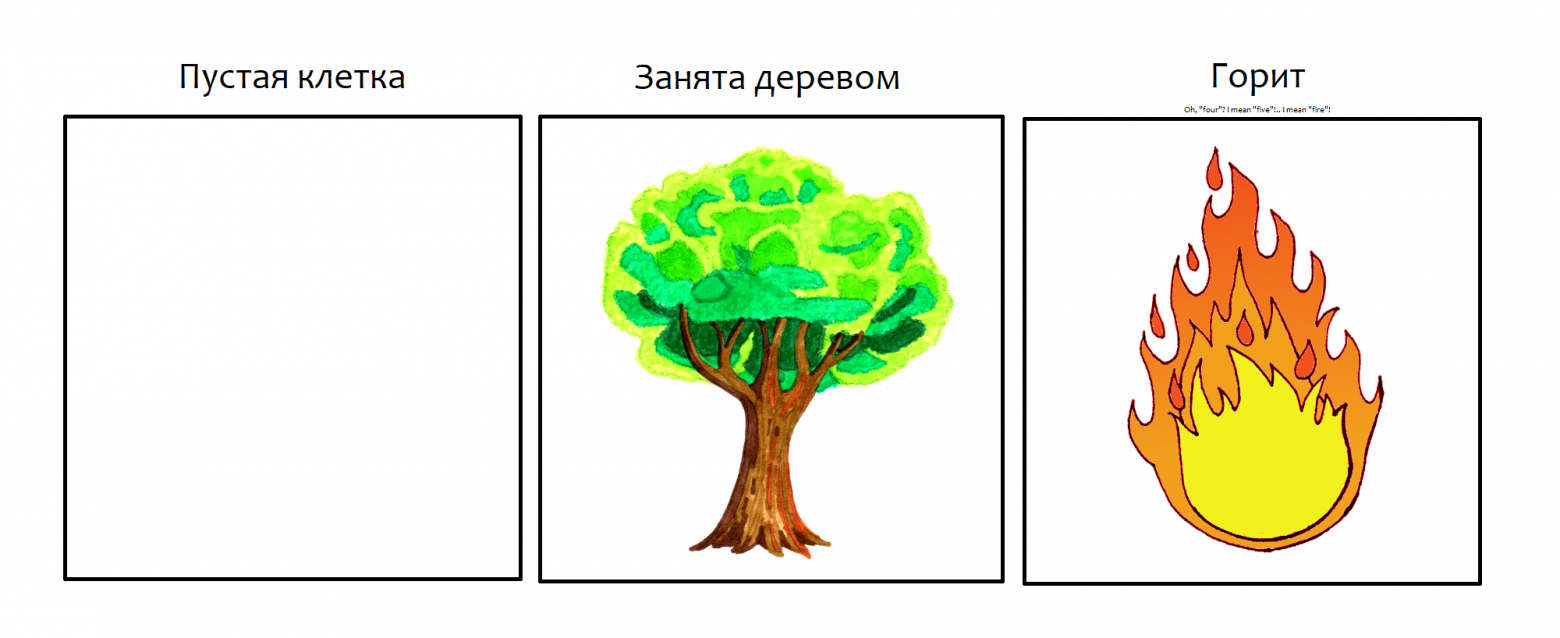
Очень идеализированный лесной пожар может быть представлен с помощью клеточного автомата. Простая модель лесного пожара на клеточном автомате состоит из сетки ячеек, где каждая ячейка может находиться в одном из трёх состояний:
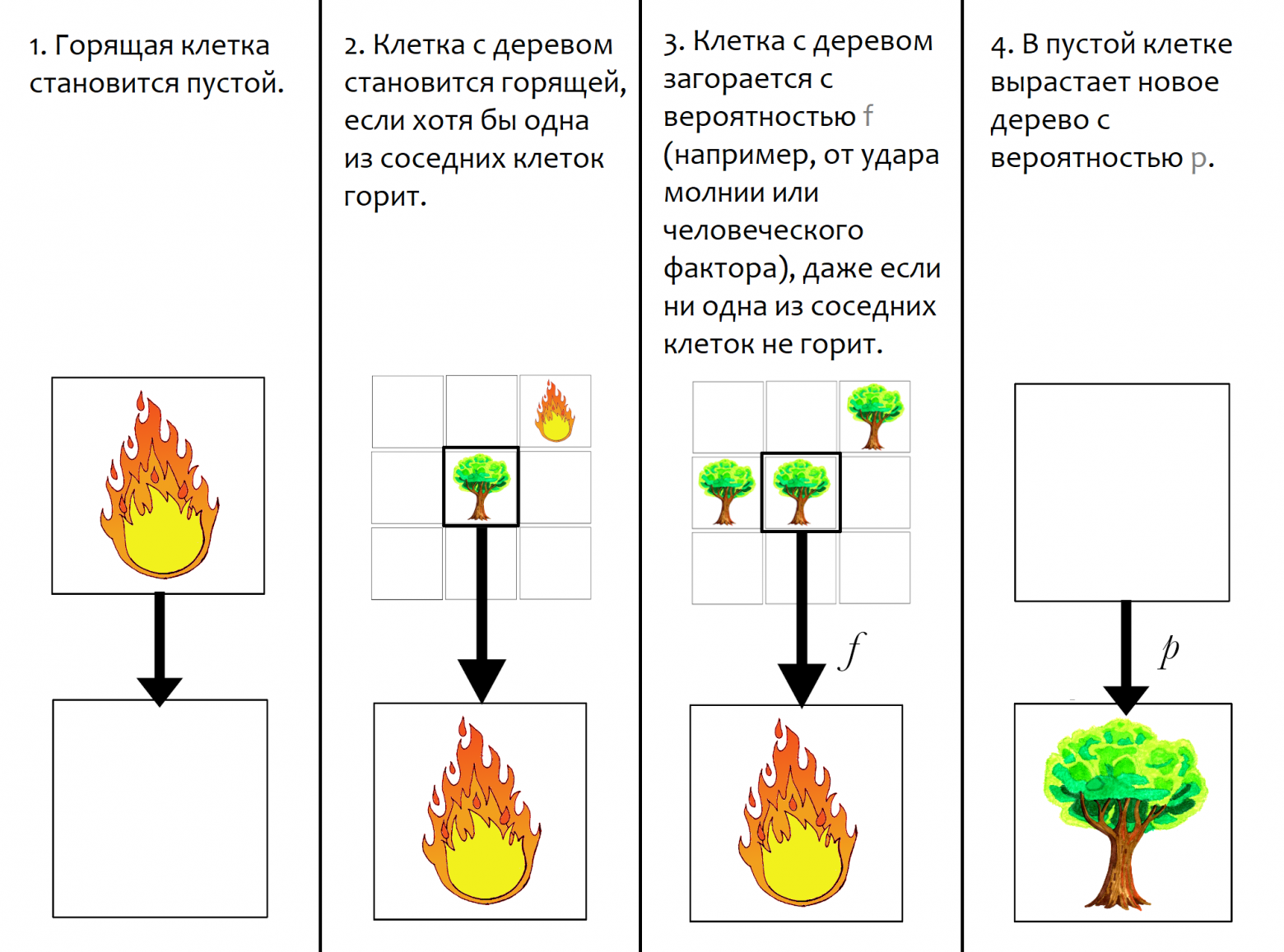
На каждом временном шаге состояние каждой клетки определяется четырьмя правилами, которые модель выполняет одновременно:
Модель лесного пожара на основе клеточных автоматов похожа на моделирование пожара на основе сетки, но не использует существующую модель распространения огня для определения скорости роста пожара. Клеточные автоматы являются примером самоорганизованной критичности и используются для моделирования нескольких природных и социальных явлений, включая лавины и эпидемии.
Да, настоящее моделирование пожаров куда сложнее
Модели пожаров также должны учитывать информацию о погоде, типе топлива (топливо – это всё, что может гореть) и топографии, которые в значительной степени влияют на рост пожара. Кроме того, "пожары создают свою собственную погоду", изменяя влажность и другие характеристики окружающей среды; это представляет серьёзную проблему для специалистов по моделированию пожаров.
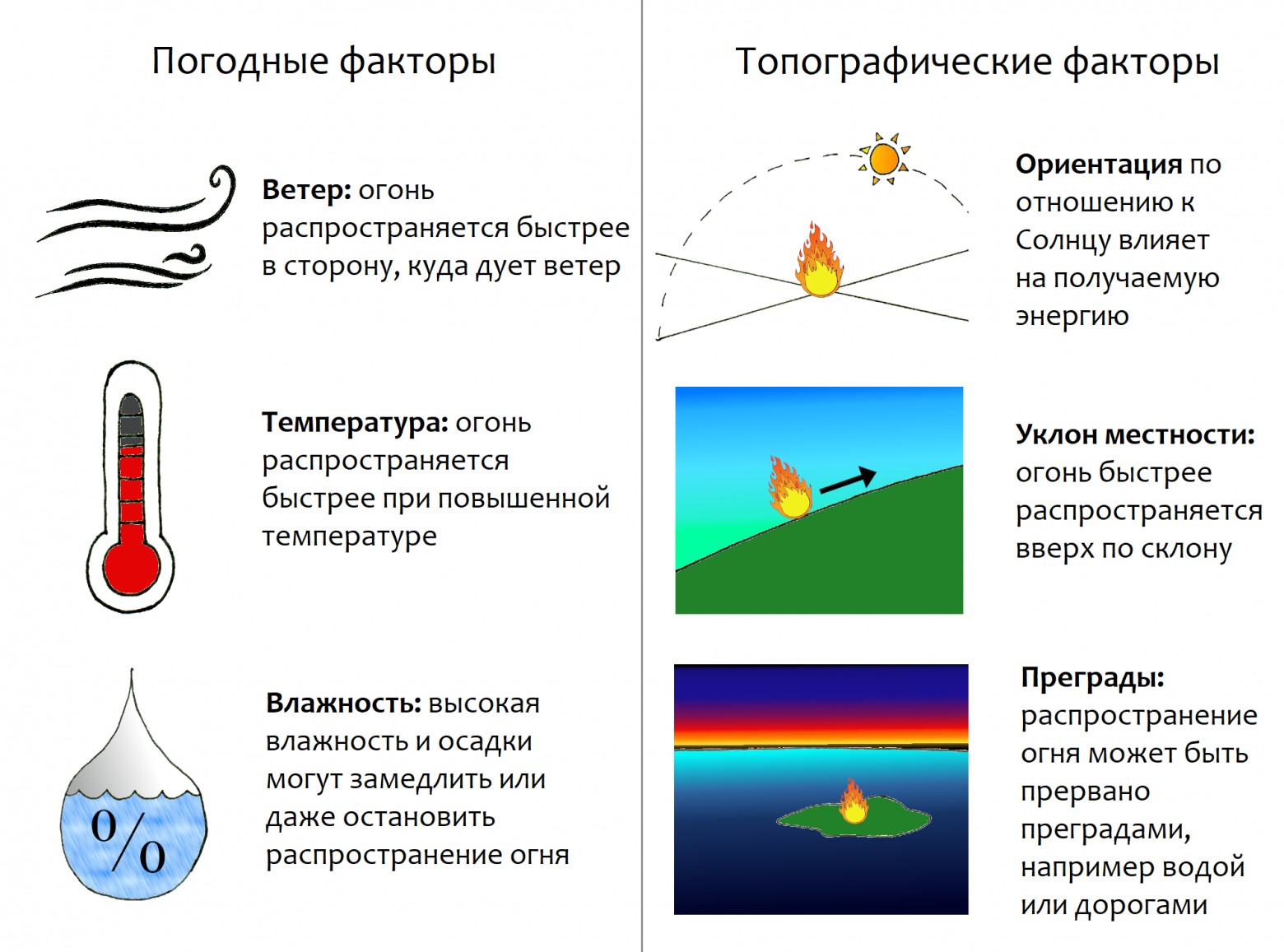
Рассмотрим FARSITE (теперь часть системы картографирования и анализа пожаров FlamMap) – известный симулятор пожара, используемый Лесной Службой США, Службой Национальных Парков и другими государственными и федеральными агентствами.
FARSITE реализует принцип Гюйгенса, используя набор дифференциальных уравнений, разработанных Г.Д. Ричардсом в 1990 году. Однако, как показано в таблице ниже, FARSITE также использует множество других уравнений, а также несколько слоёв геопространственных данных для моделирования роста пожара. Уравнения Ричардса используются только на одном этапе расчетов пожаров на поверхности и на одном этапе расчетов пожаров в кроне, что делает их относительно незначительным компонентом сложного процесса моделирования.

В моделировании пожаров важен баланс
Моделирование пожаров требует компромисса между точностью, доступностью данных и скоростью. Для реагирования на пожар в реальном времени скорость имеет решающее значение, однако самые физически сложные модели невозможно решать быстрее, чем в реальном времени. Как сказал исследователь из Университета Денвера Ян Мандел:
«Ценой дополнительной физической сложности является соответствующее увеличение вычислительных затрат, настолько, что полная трёхмерная явная обработка горения топлива в дикой природе с помощью прямого численного моделирования (DNS) в масштабах, значимых для атмосферного моделирования, не существует, находится за пределами современных суперкомпьютеров, и в настоящее время не имеет смысла делать из-за ограниченного уровня качества моделей погоды с пространственным разрешением менее 1 км.»
Следует отметить, что существует множество типов моделей поведения огня, и эти модели можно классифицировать на основе типов уравнений, которые они используют, переменных, которые они изучают, и физических систем, которые они представляют. Большинство моделей, используемых в настоящее время в США, включая FARSITE, являются полуэмпирическими. Многие вопросы о поведении огня всё ещё не решены.
→ Coding challenge
Можете ли вы построить свою собственную модель (например, клеточный автомат) для имитации распространения огня?
Какие дополнительные факторы вы можете добавить в свою модель?
Как вы их реализуете?
Сообщите о своих мыслях в комментариях!
Но давайте рассмотрим один из примеров модели клеточного автомата с четырьмя правилами моделирования пожара, который создал Кристиан Хилл.
[Следующий раздел в оригинальной статье приводит только часть реализации. Для большей полноты, раздел заменён описанием непосредственно из блога Кристиана]
Модель лесного пожара клеточным автоматом на Python
Простая модель лесного пожара определяется как двумерный клеточный автомат на сетке клеток, которые принимают одно из трёх состояний: пустая клетка, занята деревом или горит. Автомат развивается по следующим правилам, которые выполняются одновременно для каждой клетки при данном поколении:
Горящая клетка превращается в пустую клетку
Клетка, занятая деревом, становится горящей клеткой, если горит любая из восьми соседних клеток
Клетка, занятая деревом, становится горящей с вероятностью
f(даже если ни одна из соседних клеток не горит), как если бы в неё ударила молнияПустая клетка становится занятой деревом с вероятностью
p

Модель интересна как простая динамическая система, демонстрирующая самоорганизованную критичность. Следующий код Python моделирует лесной пожар с использованием этой модели для вероятностей p = 0.05, f = 0.001. Для визуализации используется анимация Matplotlib.
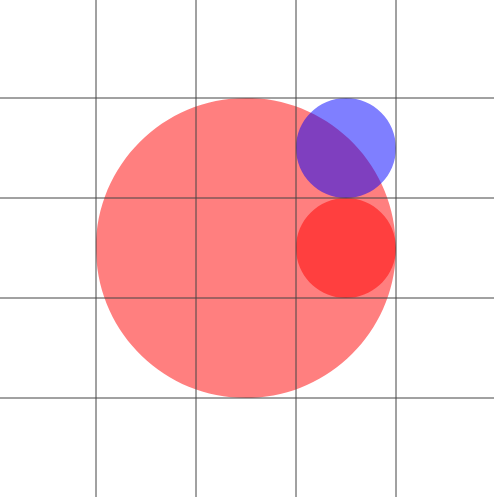
Дополнение: описанная симуляция не очень реалистична для небольших пожаров – пожары в густом лесу в такой модели имеют тенденцию распространяться в форме квадрата, потому что деревья, расположенные по диагонали, загораются так же легко, как и деревья, расположенные по ортогональной оси. Это можно улучшить, назначив вероятность возгорания этих деревьев меньше 1. Не совсем очевидно, какую вероятность назначить, но я использую 0.573. Это отношение B/A, где B – площадь перекрытия круга радиуса 3÷2 в точке (0,0) (горящее дерево) с кругом радиуса 1÷2 в точке (0,√2) (синий, диагонально примыкающее дерево), а A - площадь перекрытия этого первого круга с кругом радиуса 1÷2 в точке (0,1) (красный, ортогонально примыкающее дерево). A равна "площади" этого соседнего дерева, так как его окружность содержится в первой.
Код также доступен на Github
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation
from matplotlib import colors
# Анимация лесного пожара на основе простой модели клеточного автомата.
# Математика, лежащая в основе этого кода, описана в статье блога scipython:
# https://scipython.com/blog/the-forest-fire-model/
# Christian Hill, январь 2016.
# Обновлено в январе 2020.
# Окрестность Мура для восьми соседних клеток от рассматриваемой
neighbourhood = ((-1,-1), (-1,0), (-1,1), (0,-1), (0, 1), (1,-1), (1,0), (1,1))
EMPTY, TREE, FIRE = 0, 1, 2
# Цвета для визуализации: коричневый – пустая клетка, тёмно-зелёный – дерево
# и оранжевый – огонь. Обратите внимание, что для работы цветовой карты
# этот список и список границ должны быть на единицу больше,
# чем количество различных значений в массиве.
colors_list = [(0.2,0,0), (0,0.5,0), (1,0,0), 'orange']
cmap = colors.ListedColormap(colors_list)
bounds = [0,1,2,3]
norm = colors.BoundaryNorm(bounds, cmap.N)
def iterate(X):
"""Итерации леса в соответствии с четырьмя правилами лесного пожара"""
# Граница леса всегда пуста, поэтому рассматриваются только клетки
# с индексами от 1 до nx-2, от 1 до ny-2
X1 = np.zeros((ny, nx))
for ix in range(1,nx-1):
for iy in range(1,ny-1):
if X[iy,ix] == EMPTY and np.random.random() <= p:
X1[iy,ix] = TREE
if X[iy,ix] == TREE:
X1[iy,ix] = TREE
for dx,dy in neighbourhood:
# Соседние по диагонали деревья находятся дальше,
# поэтому загораются с меньшей вероятностью:
if abs(dx) == abs(dy) and np.random.random() < 0.573:
continue
if X[iy+dy,ix+dx] == FIRE:
X1[iy,ix] = FIRE
break
else:
if np.random.random() <= f:
X1[iy,ix] = FIRE
return X1
# Начальная доля леса, занятая деревьями.
forest_fraction = 0.2
# Вероятности роста нового дерева на пустой клетке и удара молнии.
p, f = 0.05, 0.0001
# Размер леса (количество клеток в направлениях x и y).
nx, ny = 100, 100
# Инициализируем сетку леса.
X = np.zeros((ny, nx))
X[1:ny-1, 1:nx-1] = np.random.randint(0, 2, size=(ny-2, nx-2))
X[1:ny-1, 1:nx-1] = np.random.random(size=(ny-2, nx-2)) < forest_fraction
fig = plt.figure(figsize=(25/3, 6.25))
ax = fig.add_subplot(111)
ax.set_axis_off()
im = ax.imshow(X, cmap=cmap, norm=norm)#, interpolation='nearest')
# Функция анимации: вызывается для создания кадра для каждого поколения.
def animate(i):
im.set_data(animate.X)
animate.X = iterate(animate.X)
# Привяжем нашу сетку к идентификатору X в пространстве имен функции animate.
animate.X = X
# Интервал между кадрами (мс).
interval = 100
anim = animation.FuncAnimation(fig, animate, interval=interval, frames=200)
plt.show()[Возвращаемся к изначальной статье]
Модификации модели
Водные преграды
Некоторые простые изменения в коде могут добавить в модель другие характеристики, влияющие на распространение огня. Например, чтобы добавить водные объекты, которые могут блокировать распространение огня, сначала определим новое состояние ячейки – WATER и соответствующим образом расширим список цветов и границы:
EMPTY, TREE, FIRE, WATER = 0, 1, 2, 3
colors_list = [(0.2,0,0), (0,0.5,0), (1,0,0), 'orange', 'blue']
…
bounds = [0,1,2,3,4]Затем добавим ещё одно правило в функцию итерации, которое просто гарантирует, что ячейки WATER остаются ячейками WATER.
def iterate(X):
X1 = np.zeros((ny, nx))
for ix in range(1,nx-1):
for iy in range(1,ny-1):
if X[iy,ix] == WATER:
X1[iy,ix] = WATER
…Наконец, определим границы водных объектов (в данном случае четыре вертикальных "ручья").
X[10:90, 10:15] = WATER
X[10:90, 40:45] = WATER
X[10:90, 60:65] = WATER
X[10:90, 80:85] = WATERЭти дополнения создают модель, которая показывает, как рост пожара ограничивается водой:

Примечательно, что в реальном мире огонь иногда может "перепрыгивать" через барьеры – такое поведение называется споттингом, что создает проблемы как для специалистов по моделированию пожаров, так и для спасателей.
Ветер
Оригинальная модель также может быть модифицирована с учётом ветра, который может значительно повлиять на распространение огня. Для этого сначала изменим исходную окрестность так, что NY и NX соответственно будут представлять собой первую и вторую координаты исходной окрестности.
# neighborhood = ((-1,-1), (-1,0), (-1,1), (0,-1), (0, 1), (1,-1), (1,0), (1,1))
# NY и NX теперь вместо neighborhood
NY=([-1,-1,-1,0,0,1,1,1])
NX=([-1,0,1,-1,1,-1,0,1])Чуть ниже NY и NX определим NZ, который будет представлять ветер. Каждое значение в NZ соответствует одной из координат по соседству (NY и NX). Если хотя бы одно из значений индекса в паре NY, NX, определяющих соседей, отрицательно, соответствующее значение NZ равно 0.1. В противном случае NZ равно 1. В качестве конкретного примера, первое значение NY и NX равно -1, поэтому эта первая пара координат соответствует соседу в точке (-1,-1). Таким образом, значение NZ, соответствующее этой паре, равно 0.1. Эта модификация в конечном итоге смещает распространение огня в направлении дующего ветра.
NZ=([.1,.1,.1,.1,1,.1,1,1])Последний шаг заключается в изменении функции итерации для проверки всех соседних клеток. Если сосед горит И случайно сгенерированное число меньше значения NZ соседа (0.1 или 1), то клетка загорается. Так как случайное число является плавающей величиной 0<x<1, при NZ = 1 случайное число всегда будет меньше, и клетка сгорит. Аналогично, 0.1 меньше большинства генерируемых случайных чисел. Это смещает распространение огня в зависимости от направления ветра.
def iterate(X):
X1 = np.zeros((ny, nx))
for ix in range(1,nx-1):
for iy in range(1,ny-1):
if X[iy,ix] == EMPTY and np.random.random() <= p:
X1[iy,ix] = TREE
if X[iy,ix] == TREE:
X1[iy,ix] = TREE
# Проверим все соседние клетки.
for i in range(0,7):
# Направленное распространение огня по направлению ветра.
if X[iy+NY[i],ix+NX[i]] == FIRE and np.random.random()<=NZ[i]:
X1[iy,ix] = FIRE
break
else:
if np.random.random() <= f:
X1[iy,ix] = FIRE
return X1Этот пример кода создает модель пожара с ветром, дующим равномерно с юго-востока.

Всё вместе
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import animation, colors
# Анимация лесного пожара на основе простой модели клеточного автомата.
# Математика, лежащая в основе этого кода, описана в статье блога scipython:
# https://scipython.com/blog/the-forest-fire-model/
# Christian Hill, январь 2016.
# Обновлено в январе 2020.
# Дополнения: ветер, водные преграды by Jen Ciarochi:
# https://triplebyte.com/blog/how-fire-spreads-mathematical-models-and-simulators
# Окрестность Мура для восьми соседних клеток от рассматриваемой
# neighbourhood = ((-1,-1), (-1,0), (-1,1), (0,-1), (0, 1), (1,-1), (1,0), (1,1))
# NY и NX теперь вместо neighborhood
NY = (-1, -1, -1, 0, 0, 1, 1, 1)
NX = (-1, 0, 1, -1, 1, -1, 0, 1)
NZ = (0.1, 0.1, 0.1, 0.1, 1, 0.1, 1, 1)
EMPTY, TREE, FIRE, WATER = 0, 1, 2, 3
# Цвета для визуализации: коричневый – пустая клетка, тёмно-зелёный – дерево
# и оранжевый – огонь. Обратите внимание, что для работы цветовой карты
# этот список и список границ должны быть на единицу больше,
# чем количество различных значений в массиве.
colors_list = [(0.2, 0, 0), (0, 0.5, 0), (1, 0, 0), 'orange', 'blue']
cmap = colors.ListedColormap(colors_list)
bounds = [0, 1, 2, 3, 4]
norm = colors.BoundaryNorm(bounds, cmap.N)
def iterate(X):
"""Итерации леса в соответствии с четырьмя правилами лесного пожара"""
# Граница леса всегда пуста, поэтому рассматриваются только клетки
# с индексами от 1 до nx-2, от 1 до ny-2
X1 = np.zeros((ny, nx))
for ix in range(1, nx - 1):
for iy in range(1, ny - 1):
if X[iy, ix] == WATER:
X1[iy, ix] = WATER
if X[iy, ix] == EMPTY and np.random.random() <= p:
X1[iy, ix] = TREE
if X[iy, ix] == TREE:
X1[iy, ix] = TREE
for dx, dy, dz in zip(NY, NX, NZ):
# Соседние по диагонали деревья находятся дальше,
# поэтому загораются с меньшей вероятностью:
if abs(dx) == abs(dy) and np.random.random() < 0.573:
continue
if X[iy + dy, ix + dx] == FIRE and np.random.random() <= dz:
X1[iy, ix] = FIRE
break
else:
if np.random.random() <= f:
X1[iy, ix] = FIRE
return X1
# Начальная доля леса, занятая деревьями.
forest_fraction = 0.2
# Вероятности роста нового дерева на пустой клетке и удара молнии.
p, f = 0.05, 0.0001
# Размер леса (количество клеток в направлениях x и y).
nx, ny = 100, 100
# Инициализируем сетку леса.
X = np.zeros((ny, nx))
X[1:ny-1, 1:nx-1] = np.random.randint(0, 2, size=(ny - 2, nx - 2))
X[1:ny-1, 1:nx-1] = np.random.random(size=(ny - 2, nx - 2)) < forest_fraction
X[10:90, 10:15] = WATER
X[10:90, 40:45] = WATER
X[10:90, 60:65] = WATER
X[10:90, 80:85] = WATER
fig = plt.figure(figsize=(25 / 3, 6.25))
ax = fig.add_subplot(111)
ax.set_axis_off()
im = ax.imshow(X, cmap=cmap, norm=norm) # , interpolation='nearest')
# Функция анимации: вызывается для создания кадра для каждого поколения.
def animate(i):
im.set_data(animate.X)
animate.X = iterate(animate.X)
# Привяжем нашу сетку к идентификатору X в пространстве имен функции animate.
animate.X = X
# Интервал между кадрами (мс).
interval = 100
anim = animation.FuncAnimation(fig, animate, interval=interval, frames=200)
plt.show()
Нашли опечатку или неточность в переводе? Выделите и нажмите
CTRL/⌘+Enter