Введение
Наверное, среди бывших и нынешних студентов технических университетов, найдутся те, кто помнит приятное ощущение, когда кажущаяся сложной в начале математическая конструкция разложилась по полочкам и стала предельно ясной! Попробуем сложить простую картину взаимосвязи понятной с первых курсов векторной геометрии и таких материй, как алгебры Клиффорда, кватернионы и спиноры.
Интерес начался со статьи «Единый математический язык для физики и инженерного искусства в 21 веке». Очень удобно, когда векторы можно переставлять местами в произведении и даже делить друг на друга, а повороты так и вообще задаются простейшими формулами. Но...
«Язык математики сегодня имеет много диалектов в виде различных алгебраических систем. Каждая из них разрабатывалась для решения своего класса задач и обладает своими достоинствами и недостатками» - рассказывает автор научной статьи «Геометрическая алгебра — язык творческого мышления» .
При первом прочтении этой статьи лично у меня сложилось впечатление, что все очень интересно, но очень непонятно. А когда я собрал несколько десятков книг с этими "многими диалектами", "ДЕСЯТКОВ КНИГ, И КАЖДАЯ НА НЕСКОЛЬКО СОТЕН СТРАНИЦ, КАРЛ!", то как то посвящать всю жизнь чтению, забросив работу и семью, желание не появилось.
На тот момент в моей голове, несвязанно друг с другом, проживали знания по комплексному анализу, векторной геометрии и иже с ней линейной алгебре, которые заложили еще в университете, не объяснив взаимосвязи. Так же, в общих осях, была понятна концепция кватернионов, изученная самостоятельно. Цель была - согласовать в собственной голове эти знания друг с другом, и с этой вот новой для меня дисциплиной, ради практического применения. Вот бы, думаю, найти автора, который на нескольких страницах объяснит, как это работает, чтобы не пришлось нырнуть в продвинутый математический аппарат. И частично это получилось благодаря статье «О спинорах человеческим языком». За что большое спасибо @flx0.
Если вы столкнулись с упомянутыми названиями в первый раз, то рекомендую просмотреть статьи, ссылки кликабельны.
Сокращения: АК-алгебры Клиффорда, ГП – геометрическое произведение, ГА – геометрическая алгебра
Тождество Лагранжа, разложение вектора по направлению другого вектора
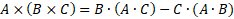
Для наглядности пусть A=C=r, B=v, где r - радиус вектор материальной точки, v - ее скорость. Далее коммутативность скалярного произведения и антикоммутативность векторного/внешнего произведения применяются без пояснений, для краткости.
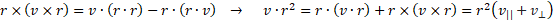
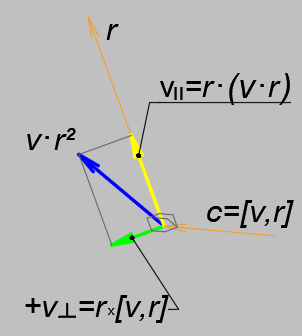
Таким образом тождество Лагранжа позволяет разложить вектор по направлениям относительно другого вектора на параллельную и перпендикулярную ему компоненту. По схеме можно проверить, что получаемые векторы — это правая тройка векторов.
Геометрическое произведение и кватернионы
Выражение похожее на «АБЦ = БАЦ минус ЦАБ» создает и геометрическое произведение (далее ГП), применяемое в алгебрах Клиффорда (далее АК), с тем отличием, что вместо векторного произведения применяется внешнее произведение.
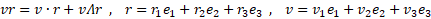
Нырнуть в математику все же пришлось, и ушло три месяца, чтобы осознать взаимосвязи. При этом оказалось, что есть нечеткость определения для внешнего произведения в русскоязычной статье в Википедии «Векторное произведение» по сравнению с определением в англоязычной статье Википедии «Geometric algebra» и учебника по геометрической алгебре и (см. в конце статьи). А в некоторых учебниках даже отождествили внешнее и векторное произведение для трехмерного пространства. Не буду их приводить, потому, что есть нюанс, но о нем позже :)
Вот что получится, если записать векторного и внешнего произведений ориентируясь на русскоязычную статье в Википедии


Из этого может неверно показаться, что

Забегая вперед правильное выражение
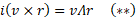
Запишем выражение для тройного ГП

Аналогичный способ изложен в статье «О спинорах человеческим языком», где вводится важное понятие |что компонента "v" параллельная "r" коммутирует, а перпендикулярная антикомутирует с "r"|, и сразу применятся

Запишем вместе выражения для двойного ГП (vr), тройного ГП (rvr) и тождества лагранжа


То есть тройное ГП означает то же, что и тождество Лагранжа, но обращенное по бивекторной компоненте, то есть “сопряженное относительно вектора r” по аналогии с комплексным сопряжением.

С учетом того, что в АК бивектор это мнимая величина и одновременно оператор поворота на 90 градусов в плоскости бивектора против часовой стрелки, это так же похоже на комплексные числа. Поэтому двойное ГП можно рассматривать как комплексное число, снабженное дополнительным свойством антикоммутативности умножения разных мнимых компонент.
Если же радиус вектор заменить на его единичный вектор, то из тройного ГП (rvr) и тождества Лагранжа получим разложение вектора скорости по направлениям этого единичного вектора в чистом виде. Что то же самое, что деление выражений выше на квадрат длины радиус-вектора.
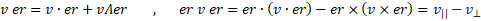

Можно видеть, что получится не одно и то же, если преобразовывать двойное и тройное ГП по формулам (*) и (**). В случае (rvr) будет получаться разный знак перед векторным произведением, а в случае (vr) векторное произведение будет вещественной или мнимой величиной.
Теперь, запишем выражение для двойного ГП и развернем его разложение по базису

Если считать бивекторы единичными кватернионами

Пересортировав, получим разложение вектора по кватернионному базису, аналогичному разложению по трем взаимно перпендикулярным комплексным плоскостям


В результате операции мы можем автоматически получать разложение движения на поступательное и вращательное. А единичные кватернионы помечены штрихами, так как через несколько абзацев появится величина без штриха. Направляющие косинусы
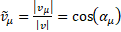
Отсюда несложным образом следует спинорное разложение, подробно изложенное в статье «Геометрическая алгебра — язык творческого мышления».
Альтернативная формулировка разложения: если еше раз пересортировать компоненты по номерам направляющих косинусов, получится нечто, что можно назвать разложением по «сдвоенным кватернионам», где вещественные компоненты так же отвечают за поступательное движение, а единичные кватернионы отвечают за вращательное движение в своих плоскостях относительно выбранного начала координат.


Например, если умножить последнее выражение на массу и квадрат радиус-вектора, то получим выражение для момента импульса сложного движения.
И вот обещанный нюанс.
Матрицы Паули в качестве спинорного базиса для разложения вектора
Было неожиданно, когда я, прочитал про связь геометрической алгебры с матрицами Паули в учебнике и потом в англоязычной статье в Википедии. До момента прочтения мне казалось, что матрицы Паули — это что-то из области квантовой физики, а именно из уравнений Максвелла. Поэтому увидев их в учебнике по математике, заинтересовался. Ведь это означает фундаментальный смысл этих матриц во всей физике, а не только в квантовой.
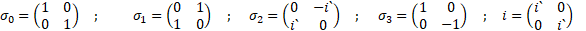
Разложение векторов, выражаясь математическим языком, в базисе матриц 2х2, выглядит так

А векторное и двойное векторное произведения в таком базисе


И, вуаля, можно видеть, что последнее является тождеством Лагранжа, правда перед тем как оно приводится в учебнике в таком виде, следует несколько страниц пояснений.
Так так как публикация не должна быть слишком длинной, вопрос базиса в матрицах 2х2 это тема для отдельного экскурса в линейную алгебру. Этот вопрос выходит за рамки данной статьи. Как и вопрос того, что в англоязычной статье в Википедии «Cross product»
Подведем итог: есть нереально удобный матаппарат, по сравнению с векторной геометрией, и им крайне мало кто пока пользуется (я узнавал у знакомых в МФТИ и МГТУ). И причин тому много. А ведь, даже в этой небольшой публикации: есть простой способ делать операцию сопряжения, есть возможность переставлять векторы в любом виде произведений, есть скалярное произведение без потери информации о координатах проекций (если все-таки не пользоваться необдумано свойством)

и все с понятной геометрической интерпретацией, при желании ее получить. Применять же можно, хоть в образовательных целях, хоть в практических, для любого направления физики связаного с векторным инструментарием.
Ссылки на источники:
1. «От алгебры Клиффорда до атома водорода» Г.Казанова, 1997.
3. «Геометрическая алгебра — язык творческого мышления»
4. «О спинорах человеческим языком»
5. «Единый математический язык для физики и инженерного искусства в 21 веке»
6. «Матрицы Паули»
7. «Векторное произведение» и «Cross product»
8. Мне лично очень помогло: «Основы теории алгебр Клиффорда и спиноров» Д.С. Широков.»












