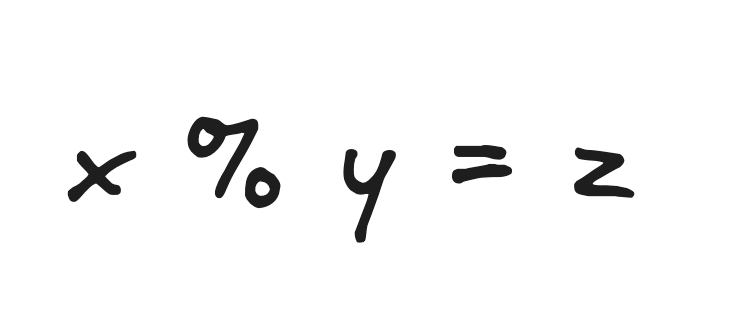
От переводчика
Всем привет, меня зовут Максим Иванов, я Frontend-разработчик, и когда-то мы с другом писали переводы на Хабрахабр. Было интересно, но в какой-то момент я прекратил эту деятельность. Спустя 5 лет я решил снова попробовать писать про мою любимую профессию. Сегодня поговорим о математическом операторе в JavaScript, который представляет из себя символ процента.
1. Введение
Когда я впервые столкнулся с оператором Modulo (%), я ничего не понял ?. Тогда я учился в 9 классе, это был 2009 год. С математикой я всегда разговаривал на "Вы", хотя для того, чтобы стать разработчиком, нужно было иметь базовые знания математики. Если у вас нет представления о том, что делает данный оператор, то для вас результаты будут казаться случайными:
const what = 10 % 4; // 2
const the = 10 % 10; // 0
const heck = 4 % 10; // 4Поэтому мы с вами разберемся как работает этот оператор через повседневную задачу деления чисел. Мы также рассмотрим практический вариант использования этого оператора в задачах во Frontend(е).
Целевая аудитория
Эта статья написана для разработчиков уровня Intern / Junior. Предполагается, что у вас есть уже некоторое знание JavaScript для понимания происходящего, но основные выводы будут полезны всем! ?
2. Математическая модель
Предположим, у нас есть некоторая арифметика вида 12 ÷ 4. Мы не будем давать теоретическое определение делению, так как деление многозначный термин, означающий распределение в разные группы. В данном случае мы хотим понять из скольких групп одинакового размера состоит число 12.
Операция 12 ÷ 4 эквивалента числу 3, поскольку каждая группа содержит 3 элемента. По сути, мы выясняем, сколько элементов будет храниться внутри каждой группы.

Наше делимое число 12 – удобное число, из которого можно легко составить несколько разных групп по 6, 4, и 3 соответственно элемента в каждом.
Предположим, что вместо этого выражения у нас есть 11 ÷ 4. Поделим на калькуляторе ?.

Легко понять, как работает деление, если мы делим пиццу или пирожное на четверых человек, но что, если предмет не так легко делим? Тут мы можем вспомнить курс школьной программы начальных классов, где мы применяли деление в столбик:

Таким образом, выражение 11 ÷ 4 дает нам две группы четверок и группу из ¾ . 3 – это остаток от деления. Смысл оператора деления по модулю в том, чтобы находить эти остатки.
В тех случаях, когда число можно поровну разделить на группы (например, как мы уже делали с 12 ÷ 4), ничего лишнего не остается, и остаток равен нулю.
12 % 4; // 0
%В тех ситуациях, когда делимое не может быть разделено поровну на группы, оператор по модулю позволяет нам узнать, сколько осталось.
11 % 4; // 33. Реальные сценарии использования в жизни
Вся эта математика конечно важна и интересна, но давайте поговорим о том, чем этот оператор может нам пригодиться в Web.
Circular Array
Есть одна из задач на Circular Array, с которой разработчики часто сталкиваются в работе или на собеседовании, где данный оператор будет вполне уместен.

Например, у нас есть массив из трех цветов. Каждую секунду мы хотим переключаться на следующий цвет в списке. Когда мы достигнем конца списка, мы хотим вернуться к первому элементу.
Как бы вы это реализовали на JavaScript без оператора по модулю? (напишите в комментариях)
Предположим, у нас есть переменная timeElapsed, которая начинается с 0 и увеличивается каждую секунду на 1. Таким образом, нам нужно сопоставить постоянно растущее значение с элементами массива, состоящим из трех элементов. По сути, нам нужно написать функцию, которая выдает следующие результаты:
const COLORS = ['red', 'yellow', 'blue'];
getColor({ timeElapsed: 0 }); // 'red'
getColor({ timeElapsed: 1 }); // 'yellow'
getColor({ timeElapsed: 2 }); // 'blue'
getColor({ timeElapsed: 3 }); // 'red'
getColor({ timeElapsed: 4 }); // 'yellow'
getColor({ timeElapsed: 5 }); // 'blue'
getColor({ timeElapsed: 6 }); // 'red'
getColor({ timeElapsed: 7 }); // 'yellow'
getColor({ timeElapsed: 8 }); // 'blue'
// ...And so on, forever
Давайте посмотрим, как оператор по модулю может помочь нам решить эту задачу:
const COLORS = ['red', 'yellow', 'blue'];
function getColor({ timeElapsed }) {
const colorIndex = timeElapsed % COLORS.length;
return COLORS[colorIndex];
}Этот код работает именно так, как нам нужно! Этот метод всегда будет возвращать один из трех цветов, если timeElapsed является целым числом. И по мере увеличения timeElapsed он будет переключаться между тремя цветами.
COLORS.length равен 3, так как в нашем массиве 3 цвета и по мере того, как timeElapsed будет увеличивается с 0, эта функция выполняет следующую последовательность вычислений:
const colorIndex = 0 % 3; // 0
const colorIndex = 1 % 3; // 1
const colorIndex = 2 % 3; // 2
const colorIndex = 3 % 3; // 0
const colorIndex = 4 % 3; // 1
const colorIndex = 5 % 3; // 2
const colorIndex = 6 % 3; // 0
const colorIndex = 7 % 3; // 1
const colorIndex = 8 % 3; // 2
// ...And so on, foreverЗатем мы можем использовать этот colorIndex для поиска цвета в массиве COLORS. Гарантируется, что цикл всегда будет находиться в пределах диапазона доступных индексов для этого массива.
Чтобы понять, почему это работает, стоит вспомнить нашу новую модель деления: мы делим timeElapsed на три группы одинакового размера, без каких-либо дробных или десятичных значений. Остаток всегда будет либо 0, 1 или 2. Он никогда не будет 3 и более, потому что, если бы остаток был 3, то в каждую группу можно было бы поместить еще по одному, что неверно математически!

По сути, мы с вами воспользовались «круговым» массивом. Независимо от того, насколько велико было бы наше базовое значение timeElapsed, мы можем бесконечно перебирать цвета в массиве COLORS.
Уже только один такой трюк делает оператор по модулю достойным того, чтобы использоваться в JavaScript! Я использовал этот трюк с круговым массивом десятки раз на протяжении многих лет, и это лишь один из нескольких практических случаев использования этого удобного оператора.
Fizz Buzz
Чтобы понять как потенциальный будущий сотрудник умеет писать код, на собеседованиях часто дают небольшие задачки на программирование. Одна из таких задач Fizz buzz используется в качестве метода проверки при найме стажеров/джуниоров.
Игроки называют числа подряд, соблюдая три правила:
Если число делится на 3, вместо него надо сказать «Fizz».
Если число делится на 5, вместо него надо сказать «Buzz».
А если число делится одновременно на 3 и на 5, то надо вместо него сказать «FizzBuzz».
Например, в этой игре первые 20 чисел будут выглядеть так:
1, 2, Fizz, 4, Buzz, Fizz, 7, 8, Fizz, Buzz, 11, Fizz, 13, 14, Fizz Buzz, 16, 17, Fizz, 19, BuzzИмея вышеперечисленный опыт и школьные знания математики, мы можем написать код, который будет делать то, что нам нужно:
function fizzBuzz(n) {
// Объявляем массив для хранения результатов
let result = [];
// Цикл от 1 до n (включительно)
for (let i = 1; i <= n; ++i) {
// Проверяем делится ли число на 3 и на 5
if (i % 3 === 0 && i % 5 === 0) {
result.push("FizzBuzz");
}
// Проверяем делится ли число на 3
else if (i % 3 === 0) {
result.push("Fizz");
}
// Проверяем делится ли число на 5
else if (i % 5 === 0) {
result.push("Buzz");
} else {
result.push(i.toString());
}
}
return result;
}Как бы вы решили эту задачу без использования оператора % (напишите в комментариях)? Так как многие задачи бывают сильно заезженными, часто интервьюеры просят продемонстрировать решение иным способом. Бывает, что некоторые хотят проверить, не зазубрили ли вы решение этой задачи. Можете ли вы придумать иной алгоритм решения?
Математическое сравнение кратности чисел с отброшенной дробной частью
Если бы в JavaScript не было оператора по модулю, то более склонные к математике люди стали бы использовать такой метод:

в меньшую сторону до ближайшего целого значения
Все что нам нужно сделать, это написать функциюmultipleOfN, которая будет определять, является ли число n кратным множителю f, и если результат n/f такой же, как иn/f с отброшенной дробной частью, то значит, что эти числа делятся без остатка. По условию задачи мы с вами уже знаем f, это 3 и 5. Таким образом, наш код после некоторых изменений легко бы работал и дальше, справляясь с данной задачей:
function fizzBuzz(n) {
let result = [];
function multipleOfN(factor, number) {
return Math.floor(number / factor) == number / factor;
}
for (let i = 1; i <= n; ++i) {
if (multipleOfN(3, i) && multipleOfN(5, i)) {
result.push("FizzBuzz");
} else if (multipleOfN(3, i)) {
result.push("Fizz");
} else if (multipleOfN(5, i)) {
result.push("Buzz");
} else {
result.push(i.toString());
}
}
return result;
}Старое школьное правило
А что если вы забыли функции функции для удаления дробной части числа посредством округления или усечения? Чтобы быстро понять, что число делится на 5 без остатка, нужно знать, что оно заканчивается на 5 или 0. Путем приведения числа в строку это можно быстро выяснить.
function multipleOf5(number) {
return ['0', '5'].includes(number.toString().at(-1));
}Но как определить, что число делится на 3 без остатка? Тут нужно вспомнить старое школьное правило, согласно которому, если сложить цифры числа и получить сумму кратную 3, тогда значит данное число кратно 3.
function multipleOf3(number) {
const total = number
.toString()
.split("")
.reduce((sum, number) => sum + Number(number), 0);
return [3, 6, 9, 12, 15, 18].includes(total);
}
Здесь кроется серьезный недостаток в решении, где список чисел кратных 3 приходится зашивать прямо в код программы из-за чего решение становится невалидным для олимпиадных задач. Так как после 18, есть еще ряд других чисел кратных тройке: 21, 24, 27, 30, ...
Однако, если в постановке задачи FizzBuzz было указано о входном счетчике первых 100 чисел, то данное решение вполне можно оценить на тройку с плюсом. Ведь если мы знаем, что последнее число 100, то оно точно не делится на 3, а делится на 5, а предпоследнее 99 число, его сумма 9+9 равна 18, что вполне входит в ту группу кратных чисел 3, которую мы зашили.
function fizzBuzz(n) {
let result = [];
function multipleOf5(number) {
return ['0', '5'].includes(number.toString().at(-1));
}
function multipleOf3(number) {
const total = number
.toString()
.split("")
.reduce((sum, number) => sum + parseInt(number), 0);
return [3, 6, 9, 12, 15, 18].includes(total);
}
for (let i = 1; i <= n; ++i) {
if (multipleOf3(i) && multipleOf5(i)) {
result.push("FizzBuzz");
} else if (multipleOf3(i)) {
result.push("Fizz");
} else if (multipleOf5(i)) {
result.push("Buzz");
} else {
result.push(i.toString());
}
}
return result;
}
Как правило, вам вряд ли повезет, ведь входным параметром могут быть числа от 1 до 104.
Card number
Частой задачей может быть форматирование номера банковской карты. На языке международных банковских стандартов номер карты называется PAN — Primary Account Number. Он может состоять из 13, 15, 16, 18 или 19 цифр. Наиболее распространенный вариант — 16. Бывает, что в базе данных хранят неформатированный PAN, однако на интерфейсе, и чтобы пользователям было удобно, вам нужно сделать некоторые преобразования. Задача состоит в том, чтобы входную строку "XXXXXXXXXXXXXXX" преобразовать подобным образом "XXXX XXXX XXXX XXXX".
function format(pan) {
return pan
.split(``)
.map((char, index) => (index && index % 4 === 0 ? ` ${char}` : char))
.join(``);
}Задача также решается с помощью оператора деления по модулю. Мы определяем позицию в строке, кратную 4, и добавляем перед символом пробел. Как бы вы решили эту задачу без оператора по модулю? (напишите в комментариях)
4. Производительность
Предположим, мы хотим сравнить, что быстрее? Использование оператора деления по модулю или использования Math.floor, который дает такой же результат.
a) от 1 до 100

b) от 1 до 1 000

c) от 1 до 10 000

d) от 1 до 100 000

e) от 1 до 1 000 000

f) от 1 до 10 000 000

g) от 1 до 100 000 000 и более

В какой-то момент мы начинаем замечать, что при сравнительно больших величинах, результаты либо начинают сравняться, либо отличаются не в столь сильный перевес. Тут можно начинать гадать, произвела ли виртуальная машина JavaScript с ее умным JIT-компилятором какие-то дополнительные оптимизации для тех или иных действий или же действительно результаты работы становятся кардинальными, когда предел стремится к бесконечности.
Важно понимать, что у разных браузеров под капотом есть своя виртуальная машина JS. Для Chrome это V8, для Firefox это SpiderMonkey, для Safari это JavaScriptCore. Поэтому всегда относитесь к JavaScript бенчмаркам с опаской, ведь на разных машинах результаты могут быть разными.
Я проводил замеры на сайте perf.link.
Built-in mod (%) function vs native mod operator
Можно пофантазировать и использовать свои функции. Например, так будет выглядеть наша функция fastMod:
function fastMod(n, factor) {
return n >= factor ? n % factor : n;
}
Согласно тестам Chandler Carruth's benchmarks at CppCon 2015, такая же функция, но уже написанная на С++ (на x86, при компиляции с Clang) давала лучший результат. Разумеется сейчас уже не 2015 год, и к тому же реализации JIT-компиляторов в JavaScript движках уже давно научились использовать более хитрые оптимизации под капотом. Но даже не прибегая к исследованиям на C++, основываясь на теории статического анализа, мы сможем объективно объяснить почему такая функция быстрее лишь потому, что она будет иметь одновременно лучший и худший сценарии использования.
5. Асимптотическая сложность
Любой алгоритм можно определить через асимптотическую сложность, которая показывает, как количество операций, выполняемых алгоритмом, будет меняться в зависимости от объема входных данных. В математике и программировании асимптотическая сложность записывается с использованием «О»-нотации. Ее ввел немецкий математик Пауль Бахман в 1894 году.
Базовое понятие статического анализа – O(1). Этот класс сложности имеют операции, которые выполняются за константное время, например, создание переменной, получение элемента коллекции или сложение небольших чисел. Если вы не знаете о каких классах сложности идет речь, можете посмотреть ролик.
Получение элемента коллекции - O(1), константный алгоритм
Перебор коллекции это O(n) - линейный алгоритм
Вложенные циклы по той же коллекции - O(n^2), квадратичный алгоритм
Бинарный поиск - O(logN), логарифмический алгоритм

а) x + y
x + y – это простое сложение двух переменных. Вне зависимости от значений x и y, для выполнения сложения требуется одна операция. Следовательно, асимптотическая сложность этого выражения - константа O(1).
const a = arr[0]; // O(1)
const b = 9 + 5; // O(1)
x + y; // O(1)UPD: Как хорошо подметили в комментариях, если у нас безразмерные целые числа, то понятно, что ты за один такт процессора их не сложить даже на современных процессорах.
@antonkrechetov: Тот, кто умеет складывать числа в столбик знает, что для получения суммы нужно сложить каждый разряд одного числа с тем же разрядом другого. Чтобы получить количество разрядов числа, нужно взять его логарифм. Так что сложность сложения двух чисел x и y произвольной длины - O(log(x + y)).
Но если мы говорим про Int64, то это определенно O(1), а если это безразмерный Int то логарифм более похож на правду.
Важно помнить, что у «О»-нотации есть три уровня оценки асимптотической сложности операций, которые показывают, какое количество может потребоваться для решения задачи:
нижняя оценка, или лучший случай — минимальное количество операций;
верхняя оценка, или худший случай — максимальное количество операций;
средняя, или средний случай — среднее количество операций.
b) x * y
Умножение двух чисел x и y имеет линейную сложность, так как требуется выполнить x умножений, чтобы получить результат. Таким образом, асимптотическая сложность умножения x * y составляет O(x) или O(y), в зависимости от того, какое из чисел больше.
c) x / y
Деление x на y также имеет линейную сложность, так как в худшем случае, если x и y равны, потребуется выполнить x делений. Таким образом, асимптотическая сложность деления x / y будет составлять O(x) или O(y), в зависимости от того, какое из чисел больше.
d) x % y
Какова асимптотическая сложность у выражения x % y? С одной стороны, мы уже изучили математическую модель и знаем, что оператор деления по модулю эквивалентен трем операциям в математике. У нас есть запись вида x = y % z , которая будет эквивалентна x = x - y * (x / y) . Таким образом, количество командных циклов будет намного больше для его вычисления. В худшем случае (x > y), операция остатка от деления может иметь линейную сложность и составлять O(x), а в лучшем случае (x < y || x = y) может быть O(1), что означает постоянное время выполнения.
Обратите внимание, что на практике асимптотическая сложность операции взятия остатка может быть оптимизирована в зависимости от аппаратной архитектуры и используемого компилятора, поэтому фактическая производительность может различаться.
Если x и y не являются переменными целого алгоритма, а будут константами в простом случае, то сложность всех вышеперечисленных операций будет O(1), потому что при постоянных величинах значения не оказывают существенное влияние на сложность. Рекомендую посмотреть еще один ролик про классы сложности, чтобы закрепить данный материал.
const x = 12;
const y = 4;
x + y; // O(1)
x * y; // O(1)
x / y; // O(1)
x % y; // O(1)6. В заключение
Буду рад комментариям, если данная статья вам была полезна. Чтобы закрепить знания, оставлю здесь задание, которое вы можете выполнить самостоятельно. Важно не прибегать к помощи Google, StackOverflow, Chat GPT, а с листком бумаги продумать, как вы можете применить оператор деления по модулю к данной задаче.
Написать функцию склонения остатка рублей на вашем счете
function declension(value, titles) {
// ...
}
declension(120_000, ['рубль', 'рубля', 'рублей']); // 120000 рублей
declension(1, ['рубль', 'рубля', 'рублей']); // 1 рубль
declension(2, ['рубль', 'рубля', 'рублей']); // 2 рубля