Привет, Хабр! Меня зовут Кирилл Колодяжный, я работаю в YADRO и продолжаю изучать машинное обучение на С++. Я уже писал, как реализовать модели для распознавания лиц на фото и для поиска объекта в пространстве с помощью computer vision. Ссылки на материалы ищите в конце статьи.
Сегодня затрону «математическую» тему и расскажу о реализации сверток: что это за операция и какие есть алгоритмы для вычисления. Приведу простые примеры с кодом, чтобы вы могли опробовать решения.
У статьи будет вторая часть: про особенности реализации одного из этих алгоритмов с использованием CUDA в рамках фреймворка PyTorch и про то, как адаптировать его под свои задачи.

Начнем с формального, но не строго математического определения.
Свертка — это интеграл от произведения двух функций после обращения и сдвига одной из них, если свертка непрерывная. В случае дискретной свертки интеграл заменяется на сумму.

Поскольку я буду рассказывать о свертке в машинном обучении, приведу и определение в ML-контексте
В ML свертка — это функция взаимной корреляции, скользящее произведение двух функций.
Чаще всего свертку можно понять как использование фильтра для обработки исходных данных или сигнала. Фильтр при взаимной корреляции не является обратным, и область пересечения между двумя функциями f и g представляет собой взаимную корреляцию.
Если рассматривать исходный сигнал как изображение, то свертку можно использовать для выделения границ. Значения фильтра, или ядра свертки, могут быть известными, как в случае с фильтром Собеля, который предназначен для выделения границ. Также эти значения могут быть изучены в процессе обучения нейронных сетей, чтобы выявлять различные особенности в данных.

Как работает свертка
Мы проходимся двумерным сигналом по каждому элементу и прикладываем фильтр. Сначала считаем в фильтре произведение, а потом сумму элементов.

У свертки есть три характерных параметра настройки:
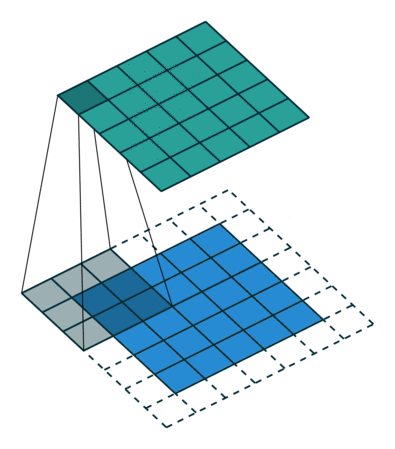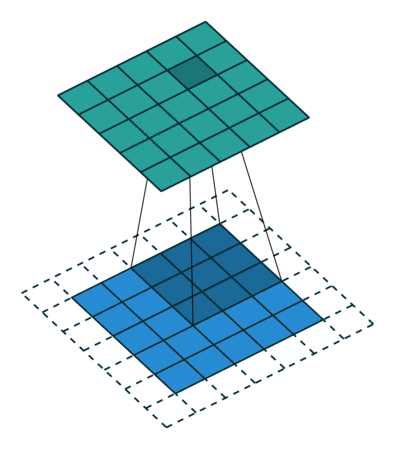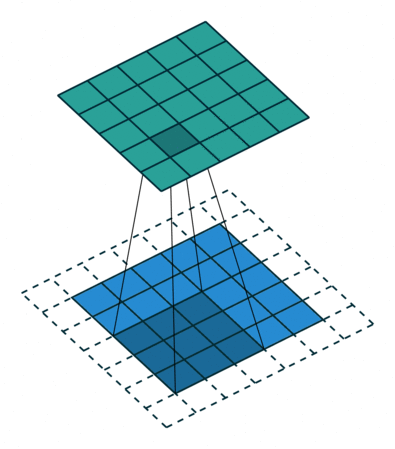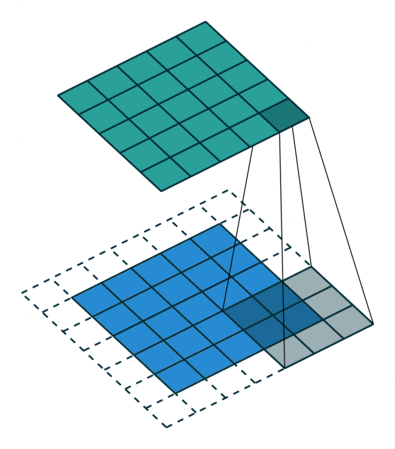
Padding — расширение исходного сигнала. Нужен для более осмысленной обработки краевых элементов.
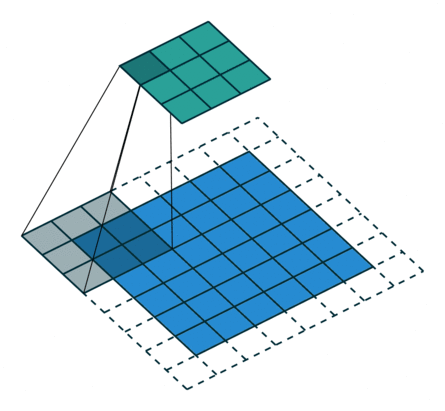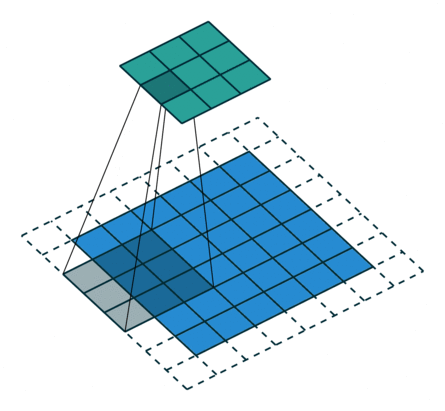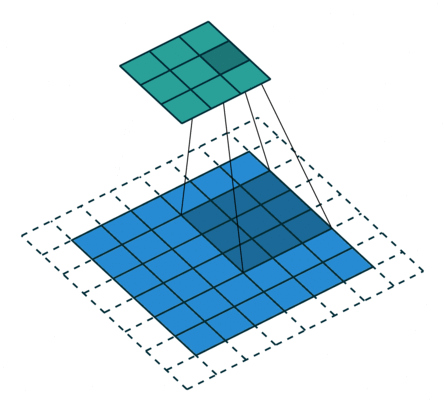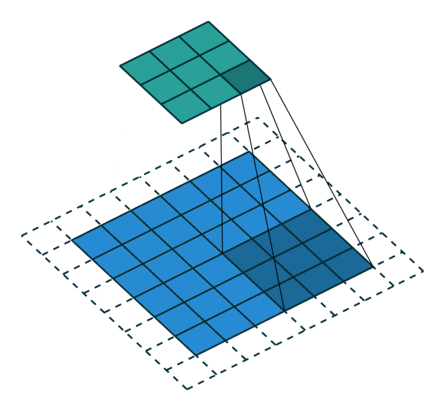
Stride — шаг свертки, который показывает, через сколько элементов применять фильтр. В примере идем через два элемента.

Dilation — инструмент для реализации разреженной свертки, он задает шаг между элементами, к которым мы применяем фильтр.
Как реализовать операцию свертки: наивный подход
Это несложная операция. Мы можем последовательно применить несколько вложенных циклов для итерации по нашим параметрам: по stride, с учетом padding и размера фильтра.
Исходные параметры:
C | Input channels |
H | Input height |
W | Input width |
N | Mini-batch size |
P | Padding |
Q | Output height |
R | Output width |
S | Stride |
U | Kernel height |
V | Kernel width |
K | Number of kernels (depth) |
Допустим, для таких исходных параметров у нас получится семь вложенных циклов, внутри которых мы посчитаем произведение, а потом сумму.

Такой подход достаточно просто реализовать на CUDA. Первое, что нужно задать для реализации на GPU — это размер grid (сетки), то есть, указать количество блоков и потоков в рамках блока:
auto num_blocks = img_height - (kernel_size - 1); // кол-во блоков = кол-ву строк auto num_threads = img_width - (kernel_size - 1); // кол-во потоков в блоке = кол-ву точек в строке auto shared_mem_size = kernel_size * kernel_size * sizeof(float); conv_img_gpu<<<num_blocks, num_threads, shared_mem_size>>>(img, kernel, img_out, img_width, img_height, kernel_size);
Мы пройдемся по каждой строке изображения (в статье я называю исходный сигнал изображением) и в каждом пикселе применим фильтр. Сходу можно предложить такую оптимизацию: разместить ядро в shared-памяти (локальной памяти) наших блоков, чтобы каждый раз не грузить его из глобальной памяти. Это увеличит производительность реализации.
Здесь представлен код как раз самого ядра (kernel) — функции, которая будет вычисляться в одном потоке на GPU.
__global__ void conv_img_gpu(float* img, float* kernel, float* img_out, int width, int height, int kernel_size) { auto tid = threadIdx.x; // локальный ID потока внутри блока auto y = blockIdx.x + (kernel_size - 1) / 2; // блок связан со строкой изображения, Y auto x = threadIdx.x + (kernel_size - 1) / 2; // поток связан с пикселем изображения в строке, X auto idx = y * width + x; // глобальный индекс пикселя по всем блокам auto k_num_el = kernel_size * kernel_size; // количество элементов ядра auto center = (kernel_size - 1) / 2; // центр ядра по двум измерениям extern __shared__ float sdata[]; // shared memory для значений ядра if (tid < k_num_el) sdata[tid] = kernel[tid]; // перенос значений ��дра из глобальной памяти __syncthreads(); // синхронизация потоков - ждем заполнения smem ... }
Вычисляем функцию:
Вычисляем индекс данных, которые будет обрабатывать этот поток.
Исходя из индекса блоков, вычисляем, какая это строка и какой пиксель в изображении начальный.
Далее в строке с ключевым словом
__shared__описываем shared-память — туда положим данные фильтра.Далее задаем if, который проверяет, что индекс потока не превышает количество данных из фильтра — это нужно, чтобы не выйти за границы пределов памяти.
Добавляем операцию синхронизации потоков.
Синхронизация потоков нужна, чтобы перенести данные из глобальной памяти в shared-память. Это убережет от «гонок» при обращении к еще не заполненной shared-памяти. Все потоки дойдут до этой синхронизации, а потом продолжат выполнение.
К этому моменту мы перенесем все данные из глобальной памяти в shared и дальше сможем использовать значение нашего фильтра. У нас просто есть два цикла по размерам фильтра. В примере ниже используется одно значение размерности, так как я предполагаю квадратный фильтр. И в нем точно так, как в псевдокоде выше, мы считаем произведение, прибавляем его к сумме и накапливаем результат.
__global__ void conv_img_gpu(...) { ... float sum = 0.0; if (idx < width * height){ for (int k_y = 0; k_y < kernel_size; k_y++) for (int k_x = 0; k_x < kernel_size; k_x++){ auto img_x = k_x + x - center; auto img_y = k_x + y - center; sum += img[img_y * width + img_x] * sdata[k_y * kernel_size + k_x]; } img_out[idx] = sum; } }
Недостатки простого подхода
Вычислительная сложность:
Arithmetic Intensity (AI):
Особенности архитектуры GPU учитываются не полностью.
Не учитываются различные размеры ядер и изображения.
Не работает с дополнительными параметрами свертки.
Есть ли подход, который учитывает все недостатки простого метода? Давайте разберемся.
Альтернативные подходы
Winograd
Один из альтернативных подходов — алгоритм Winograd, названный в честь автора Шмуэля Винограда. Это математик, который работал в области вычислительной сложности и анализа алгоритмов.
Сам алгоритм заключается в том, что мы переводим значение сигнала и фильтра в другое пространство — Winograd, где операцию свертки можно заменить на поэлементное умножение. Для этого нужно специальным образом подготовить матрицы преобразования. Если кратко то на основе выбранных начальных точек строится многочлен Лагранжа, он используется для получения матрицы Вандермонда, которая потом раскладывается в матрицы A, B, G. Для детального описания подхода можно обратиться к например к этой статье.

На картинке видим такие матрицы для размера фильтра 2х2 и регион изображения 3х3.
Как работает алгоритм:
Делим изображение на тайлы.
Применяем преобразование с помощью матрицы преобразования отдельно для тайла, отдельно для фильтра.
Перемножаем их.
Делаем обратное преобразование и собираем финальный результат.
x-data, f-filters * - elementwise multiply 1: F = G f G^T 2: s{a,b,c,...} = SplitInTiles(x) 3: R{} = results 4: for k to Ns do 5: R[k] = B s[k] B^T * F 6: end 7: for k to Ns do 8: R[k] = A^T R[k] A 9: end 10: R = CombineFinalResult(R)
Подход основан на теореме Шмуэля Винограда: «Линейная свертка двух последовательностей может быть представлена в виде двух полиномов с коэффициентом, соответствующим исходным последовательностям. И это можно реализовать с меньшим количеством операций умножения».
Этот подход позволяет существенно уменьшить количество операций умножения, заменив их операциями сложения. То есть амортизированная сложность с учетом того, что у нас предвычисленная матрица, существенно меньше, чем у наивного подхода.
Однако тоже есть определенные ограничения:
Матрицы A, G, B рассчитываются заранее, их размер зависит от размера ядра — для больших ядер размер тоже будет большим.
Сложно реализовать для параметров свертки, не равных 1.
Амортизированная сложность:
Быстрое преобразование Фурье
Следующий алгоритм для быстрого вычисления свертки — быстрое преобразование Фурье. Суть та же:
Преобразуем значение сигнала и фильтра в другое пространство, где можем произвести поэлементное умножение, только в этот раз комплексное.
Делим изображение на тайлы.
Делаем преобразование Фурье.
Производим умножение со значениями фильтра.
Делаем обратное преобразование и комбинируем результат.
x-data, f-filters * - complex elementwise multiply 1: F = FFT(f) 2: s{a,b,c,...} = SplitInSegments(x) 3: S{A,B,C,...} = FFT(s) 4: R{} = results 5: for k to Ns do 6: R[k] = S[k]*F 7: end 8: R = InverseFFT(R) 9: for k to Ns do 10: RemoveAliasedsamples(R[k]) 11: end 12: R = CombineFinalResult(R)
Это можно изобразить следующей схемой:

Слева на картинке изображен фильтр. При использовании подхода с FFT нам нужно добавить padding и к исходному сигналу, и к фильтру, чтобы согласовать их размерности. После чего сделать преобразование фильтра в частотное пространство. И дальше двигаемся окном по исходному сигналу, делаем FFT-преобразование, производим умножение с фильтром и формирование выхода.

Надо сказать, что подход работает намного быстрее, чем наивная реализация. Вычислительная сложность алгоритма — O(N^2 log(N). Но есть ограничение: он будет требовать намного больше памяти. Это связано с тем, что сам преобразованный сигнал в преобразовании Фурье будет занимать больше памяти. В зависимости от выбранного подхода мы должны идти окном по исходному сигналу с перекрытием.
Таким образом, у нас будут получаться дополнительные области памяти, ненужные для формирования выходного сигнала, но нужные для работы алгоритма.

Подход на основе General Matrix Multiplication
Следующий подход основан на быстром вычислении операции GEMM (General Matrix Multiplication):
𝐶←𝛼𝐴𝐵+𝛽𝐶
Это операция — одна из функций библиотек для линейной алгебры, реализующих интерфейс BLAS (Basic Linear Algebra Subprograms). Представляет собой взвешенное произведение матриц со сложением в аккумулятор (третью матрицу), также умноженное на коэффициент. В целом вычислительная сложность умножения матриц — это или
, если у нас квадратная матрица.
Однако есть на данный момент алгоритмы и побыстрее. По-моему, самый лучший результат сейчас — это примерно . Что еще хорошо: у операции матричного умножения высокая арифметическая интенсивность:
Разобраться, как происходит умножение матриц на примере T-Head Matrix Extension, можно с помощью материала моего коллеги Андрея Соколова.
Арифметических операций намного больше, чем обращений в память, — значит, мы можем потенциально хорошо ее распараллелить.
Эта операция реализована во многих библиотеках — от тех, которые работают на CPU, до GPU и специальных вычислителей. Это OpenBLAS, cuBLAS, Cutlass, Intel MKL, rocBLAS. Т.е. она эффективно реализована под разные программные фреймворки и аппаратные реализации.
Суть распараллеливания заключается в том, что мы разделяем операцию умножения на отдельные блоки.

Перемножение строки и столбца делим на отдельные блоки, и вот эти маленькие матричные умножения разносим на разные потоки вычисления. В рамках этих потоков мы также можем использовать специальные, хорошо оптимизированные инструкции для вычисления. Например, тензорные ядра, операции MMA (Matrix multiply-add) или Fused multiply-add-операции.
Чтобы использовать операцию GEMM для вычисления свертки, нужно преобразовать как изображение, так и фильтр в формат, подходящий для матричного умножения. Перемножить напрямую мы их, конечно, не можем. Существует подход, называемый Image to column (im2col) или Volume to column (vol2col), который описывает, каким образом нам преобразовать исходное изображение в подходящую матрицу для операции GEMM.
Здесь представлен результат преобразования изображения 3х3 с padding = 1 в такую матрицу 9х9:

Мы видим, что многие элементы здесь повторяются. Это происходит из-за того, ��то фильтр движется скользящим окном и вычисление производится с этими же элементами.
Отсюда следует одно из основных ограничений этого алгоритма: он требует достаточно много памяти из-за повторяющихся элементов в построенной большой матрице. Однако это компенсируется очень быстрым вычислением операции GEMM. Плюс алгоритм подвержен «проклятию размерности».

Если мы увеличим количество, допустим, слоев, у нас будет трехмерная свертка. А если еще используем достаточно много батчей, матрица будет пропорционально сильно расти.
Но есть способ решения проблем с потреблением памяти — мы не обязаны хранить всю эту большую матрицу в памяти.
Implicit GEMM
Существует подход, продолжающий GEMM, — обычно его называют Implicit GEMM. Суть в том, что мы не вычисляем сразу всю большую матрицу свертки. Мы ее будем вычислять по мере работы потоков, динамически загружать нужные нам блоки в shared memory и потом эффективно их вычислять. Этот подход более подробно разберем во второй части.
Сравнение подходов
Наивный подход, несмотря на его недостатки, используется нередко. Он реализован в cuBLAS и будет работать для небольших размерностей ядер и данных.
Алгоритм Winograd очень эффективный, но используется для маленьких ядер, так как для больших размеров ядер матрица для преобразования будет сильно расти. Плюс у подхода часто ограниченный набор параметров для свертки.
Алгоритмы, основанные на преобразовании Фурье, подходят для больших ядер, для больших размерностей входных данных, но требуют достаточно много памяти.
GEMM, по ограничениям похож на FFT. Работает с любым набором параметров, с любыми размерностями, если вам хватает памяти. Самое распространенное применение — вариант с Implicit GEMM, потому что он работает достаточно гибко, обрабатывает и маленькие, и большие, и средние размеры, требует не так много памяти.
О том, как реализовать свертку в CUDA, я расскажу в следующей части. А пока изучите другие мои работы о машинном обучении на «плюсах»: