Надоели нестабильные баги в многопоточном коде? Попробуй воспользоваться модел-чекерами! Ведь больше не надо бояться неверифицированных модел-чекеров, работающих либо за экспоненциальное время, либо неоптимально. Все это в прошлом: в Max Planck Institute for Software Systems разработали новый алгоритм под названием TruSt, который решает эти проблемы и, кроме того, верифицирован на Coq.
Меня зовут Владимир Гладштейн. Этим летом я проходил стажировку в MPI-SWS в группе, которая придумала алгоритм нового модел-чекера для поиска багов в многопоточных программах. Этот алгоритм является оптимальным и truly stateless (вследствие чего работает с линейными затратами по памяти). В этом посте я расскажу, как работают модел-чекеры, в каких случаях их можно использовать, и что за алгоритм придумали мои коллеги. А еще как я проверял доказательства его корректности на Coq.

О себе
Я учусь на 4-ом курсе программы «Математика, алгоритмы и анализ данных» факультета математики и компьютерных наук СПбГУ, а также работаю в Лаборатории языковых инструментов JetBrains Research. Я больше двух лет изучаю формальную верификацию программ и в основном пишу на языке Coq.
О стажировке
Этим летом мне посчастливилось пройти стажировку в Max Planck Institute for Software Systems. Попал я туда неслучайно. Дело в том, что Лаборатория языковых инструментов JBR тесно сотрудничает с этим институтом. В частности, руководитель моей группы Антон Подкопаев был постдоком у профессора MPI Виктора Вафеядиса. Поэтому с рекомендацией от Антона на меня быстро обратили внимание и устроили собеседование с Виктором. В итоге меня зачислили стажером на два месяца — с июля по август 2021 года. Стажировка проходила дистанционно.
О проекте, в котором я работал
В начале лета команда в MPI-SWS, к которой я присоединился, готовилась к подаче статьи на конференцию POPL. Если вкратце, они придумали алгоритм нового модел-чекера (далее МС) для поиска багов в многопоточных программах и предложили мне формально проверить доказательства его корректности на Coq. Этой задачей я и занимался.
Но давайте обо всем по порядку. Начнем с Coq.
O Coq
Coq — это функциональный язык программирования с очень мощной системой зависимых типов. С помощью нее по соответствию Карри-Говарда в Coq удается формулировать и на специальном языке записывать доказательства теорем, которые он сможет проверить. Примеры формулировок теорем в Coq у нас еще будут, а пока, чтобы представлять о чем речь, можно почитать начало мягкого введения. Главное, что тут надо понять — на этом языке можно написать доказательство теоремы, и он его проверит. Среди CS сообщества считается, что теоремы, проверенные на Coq, не содержат ошибок в доказательствах.
О багах в многопоточном коде
Думаю хаброжители знают, что многопоточные программы — это штука сложная. Иногда в них появляются баги, которые очень тяжело отловить тестами. Такие баги могут появляться пару раз на тысячу запусков программы, однако, если ей ежедневно пользуется порядка десяти тысяч человек, то хочется как-то баг отловить и исправить. Одним из решений как раз являются MC.
Давайте разберем пример такой программы. Пример довольно объемный, но он поможет понять, в каких случаях разумно использовать модел-чекеры. Если хотите пропустить пример, жмите сюда.
Представьте себе любимый банк. А теперь представьте, что вас назначили программистом в этом банке и попросили написать код для обслуживания очередей. Человек приходит в банк, берет номерок и ждет своей очереди.
Условно ваша программа должна уметь:
Хранить номер билетика, который будет выдан следующему человеку;
Хранить номер билета человека, которого сейчас обслуживают;
Выдавать новые билеты;
Менять номер обслуживающегося билета.
Давайте попробуем написать такое на C, используя многопоточность. Сначала заведем структуру, описывающую память нашего автомата по выдаче билетов:
struct ticketlock_s {
atomic_int next; // номер билета, который будет выдан следующему человеку
atomic_int owner; // номер билета у человека, которого сейчас обслуживают
};Так как мы будем писать многопоточный код, в котором поля данной структуры будут шариться между потоками, нам необходимо сделать их не просто int, a atomic_int.
Теперь давайте опишем процедуру выдачи билета человеку с его последующим ожиданием своей очереди:
static inline void ticketlock_lock(struct ticketlock_s *l)
{
int ticket = atomic_load(&l->next); // получаем номер следующего билета
atomic_store(&l->next, ticket + 1); // увеличиваем номер следующего билета на 1
while (atomic_load(&l->owner) != ticket) { // человек ждет своей очереди
}
}Теперь можно описать процедуру перехода очереди от одного человека к другому:
static inline void ticketlock_unlock(struct ticketlock_s *l)
{
int owner = atomic_load(&l->owner); // получаем номер обслуживаемого человека
atomic_store(&l->owner, owner + 1); // увеличиваем номер
}Для простоты будем считать, что обслуживание человека заключается в том, что он кладет одну денежку на некоторый счет x, а потом происходит проверка, что значение x действительно увеличилось на один:
int thread(void* unused) {
ticketlock_lock(&lock); // человек получает номерок и ждет
int y = x++; // сохраняем значение x в y и кладем 1 денег на x
assert(x == y + 1); // проверка, что на x было положено 1 денег
ticketlock_unlock(&lock); // зовем следующего
return 0;
}Однако наш банк должен обслуживать много людей, поэтому, чтобы смоделировать его работу, надо запустить процедуру thread в нескольких потоках одновременно:
void test() {
ticketlock_init(&lock); // инициализируем поля нулями
thrd_t threads[N_THREADS]; // создаем несколько потоков
for (int i = 0; i < N_THREADS; ++i) {
int err = thrd_create(&threads[i], thread, NULL); // запускаем во всех потоках thread
if (err) {
abort();
}
}
// сливаем потоки
for (int i = 0; i < N_THREADS; ++i) {
thrd_join(threads[i], NULL);
}
}Как мы хотим, чтобы работала наша программа? Рассмотрим на примере двух потоков (N_THREADS = 2).
Будем придерживаться модели памяти Sequential Consistency (то есть можно считать, что при запуске программы инструкции разных потоков перемешиваются, сохраняя свой порядок внутри одного потока, и запускается однопоточный код).
Допустим в банк пришли Петя (первый поток) и Вася (второй поток). В нормальной ситуации они находятся сначала на строке:
ticketlock_lock(&lock);Предположим, что сначала работает первый поток (то есть Петя первый взял билетик):
int ticket = atomic_load(&l->next);
atomic_store(&l->next, ticket + 1)Он получает билет номер 0, и следующий билет будет уже иметь номер 1. Потом, например, сюда может встроиться Васин (второй) поток и оттуда выполнится три строчки (Вася возьмет свой билет и сядет в очередь):
int ticket = atomic_load(&l->next); // Вася получает билет номер 1
atomic_store(&l->next, ticket + 1); // следующий билет теперь имеет номер 2
while (atomic_load(&l->owner) != ticket) { // owner равен 0, поэтому Вася ждет, пока не продолжит работать Петин поток
}Наконец встраивается первый поток: Петя спокойно перескакивает бесконечный цикл (а не садится туда ждать), потому что номер его билета совпадает с номером билета, который будут обслуживать.
while (atomic_load(&l->owner) != ticket) { // условие не срабатывает, потому что owner = 0, а у Пети как раз билет номер 0
}Далее первый поток выходит из ticket_lock и начинается обслуживание Пети:
int y = x++; // Петя положил денежку на счет x
assert(x == y + 1); // все хорошо: x = 1, y = 0
ticketlock_unlock(&lock); // зовем ВасюТут Васин поток не может никуда встроиться до того, как мы выполним ticketlock_unlock(&lock), потому что пока в Петином потоке не выполнится ticketlock_unlock(&lock), номер Васиного билета (1) не совпадет с номером обслуживаемого человека (0), и Вася не сможет выйти из цикла . Также ясно, что assert не нарушится, потому что сначала Петя увеличит значение x (там будет 1, а в y — 0), потом то же самое сделает Вася.
Это хорошее поведение программы, так как хоть потоки и исполняются параллельно, мы не можем начать обслуживать Васю, пока не закончим обслуживать Петю.
Теперь вопрос: может ли когда-то нарушится проверяемый assert? И ответ: к сожалению, да. На самом деле этот assert нарушается ровно тогда, когда в процесс обслуживания одного клиента встраивается обслуживание другого. Давайте посмотрим, как это может произойти в случае, если у нас два потока.
Предположим теперь, что сначала в первом потоке выполняется первая инструкция ticketlock_lock:
int ticket = atomic_load(&l->next); // Петя получает билет с номером 0Потом сразу вмешивается второй поток, и там выполняются первые две инструкции:
int ticket = atomic_load(&l->next); // Вася тоже получает билет с номером 0
atomic_store(&l->next, ticket + 1); // номер следующего номера теперь 1Наконец, выполняется следующая инструкция первого потока:
atomic_store(&l->next, ticket + 1); // в номер следующего потока снова записывается 1Далее ни один из потоков не зависает в цикле while, и они оба выходят из ticketlock_lock. Это плохо, потому что теперь мы можем случайно начать обслуживать их одновременно, а это иногда приводит к разного рода ошибкам (в частности, нарушения assert’a).
События могут развиваться как-то так: сначала, первый поток продолжает
int y = x++; // Петя положил денежку на счет xТут сразу встроился Вася:
int y = x++; // обслужили Васю: увеличили xИ в итоге в первом потоке в y находится 0, а х уже равен 2, что ведет к невыполнению assert’a.
Ясно, что тут возникла проблема, потому что Вася получил свой билет до того, как наша программа успела до конца обработать получение билета Петей. Поэтому чтобы ее решить, надо просто сделать так, чтобы один поток не мог влезть между двумя инструкциями, отвечающими за выдачу билета, пока их исполняет другой поток. А именно:
int ticket = atomic_load(&l->next);
atomic_store(&l->next, ticket + 1);Для этого можно их объединить в одну атомарную инструкцию:
int ticket = atomic_fetch_add(&l->next, 1);«Плохой» способ выполнения программы происходит достаточно редко, так что тестами его отловить непросто. Именно поэтому тут нужен какой-нибудь другой путь проверки ее корректности.
О Model Checker
Чтобы ловить такие баги, можно использовать MC. Что они делают? Это специальные программы, которые на вход берут ваш многопоточный код и стараются некоторым способом обойти все возможные сцены его исполнения (может быть по модулю некоторой эквивалентности). Для того чтобы понять, как они работают, давайте обратимся к семантике многопоточных программ.
О семантике многопоточных программ
Каждой многопоточной программе можно поставить в соответствие некоторый «граф исполнения». Каждый такой граф описывает определенное множество исполнений программы, ведущих к одному и тому же результату. То есть если у вас есть на руках такой граф, вы можете «почти» сказать, как исполнилась программа, но этого «почти» хватает, чтобы например понять, нарушались ли какие-то assert’ы или нет.
Пример: рассмотрим программу на неком псевдоязыке:
x := 0
x:= 1 || x:= 2
r := x
assert (r!=1)Тут мы сначала записываем в x 0, потом в двух разных потоках пишем 1 и 2, и в конце читаем из x.
Этой программе соответствует несколько «графов исполнения». Например, такой:
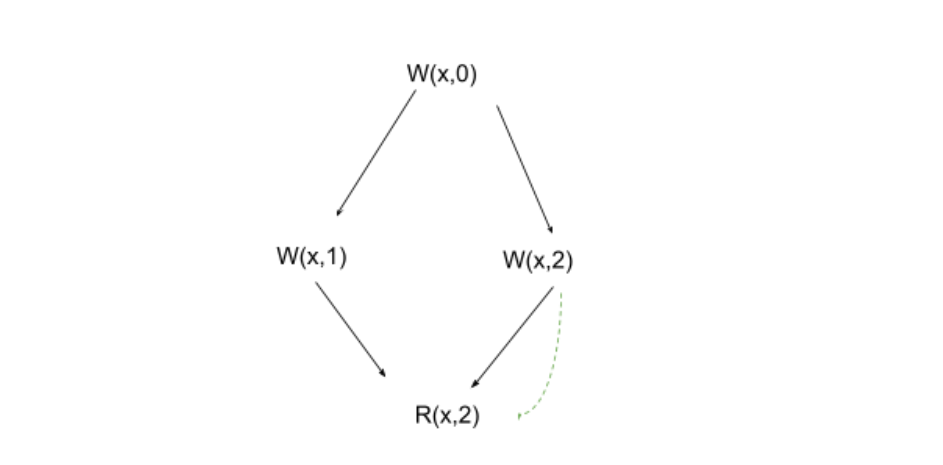
В этом графе есть два типа вершин, они называются событиями:
W(x,i)— запись в переменную x числа i (например, инструкцииx := 0соответствуетW(x,0));R(x,j)— чтение из переменной x числа j (например, если мы вr := xпрочитали 2, то этому будет соответствовать R(x,2)).
И два типа ребер:
Серые — program order. Они соответствуют порядку инструкций (например x:=1 идет после x:=0, поэтому между ними стоит стрелка);
Зеленые — reads from. Они показывают, откуда событие чтения берет свое значение (в данном случает r := x читает из x:= 2).
Смотря на этот граф, легко понять, что assert не срабатывает.
О моделях памяти
Запуская один и тот же код на разных языках или на разных процессорах, мы можем наблюдать разные поведения. Почему так происходит? Дело в том, что над вашим кодом компилятор, а потом и сам процессор могут проявлять разного рода оптимизации. Эти оптимизации изначально были написаны для однопоточного кода, поэтому они могут привести к тому, что программа поведет себя совсем не так как вы хотите (подробнее тут). Ну и отличия в поведениях программ как раз обуславливаются тем, что при разных энвайронментах эти оптимизации разные. Модели поведения многопоточных программ называются моделями памяти (далее MM). Самая простая и известная MM — это Sequential Consistency.
Если мы хорошо изучим конкретную ММ, то сможем по графу исполнения программы говорить, допустим он или нет при данной ММ. Поэтому ММ часто моделируются просто предикатами на графах.
О проблемах model checker
Итак, задача MC заключается в переборе всех возможных графов соответствующих данной программе.
MC можно оценивать по большому количеству параметров, вот три из них:
Оптимальность: так как MC занимается обходом графов, можно говорить, что он оптимален если обходит каждый граф соответствующий программе ровно один раз
Stateless/explicit-state: MC может хранить какие-то данные о графах, которые он уже обошел. Если он вообще никакой информации не хранит, то будем называть его Stateless.
Параметричность по MM: будем говорить, что МС параметричен по MM, если он работает для различных MM. Математически это моделируется так, что MC принимает на вход некоторый предикат на графах исчисления
consи дальше исследует графы, соответствующие этому предикату.
Самые успешные существующие MC являются параметричными по модели памяти, оптимальными и почти Stateless. То есть они не посещают одни и те же графы несколько раз, однако, хранят какую-то информацию о своей предыдущей работе, что ведет к экспоненциальным затратам по памяти.
О TruSt
Наконец, новый алгоритм, который был разработан в MPI-SWS, является первым оптимальным, параметричным по модели памяти и в то же время Stateless (вследствие чего имеет линейные затраты по памяти). Поэтому он и называется TruSt (Truly Stateless).
Tут, однако, стоит отметить, что он работает не для всех моделей памяти, а лишь для тех, которые удовлетворяют некоторым условиям. Сюда подходят такие модели памяти, как Sequential consistency (SC), Total store ordering (TSO) (еще про эту модель можно почитать тут), Partial store ordering (PSO), а также фрагмент модели памяти языка С/С++ (RC11).
MC ищет ошибки в многопоточной программе, но кто гарантирует, что в самом алгоритме МС нет ошибок? Ведь если они есть, model checker может ввести пользователя в заблуждение. Поэтому важно формально верифицировать МС. Как раз этим я и занимался. Я взял псевдокод, на котором алгоритм был представлен в статье, закодировал это в Coq и формально проверил некоторые теоремы о корректности этого алгоритма.
К сожалению, сам алгоритм устроен довольно сложно, и я не смогу его здесь описать. Все подробности можно найти в статье. А сейчас я расскажу достаточно общую схему того, как он был закодирован на языке Coq.
Зафиксируем для начала некоторый предикат модели памяти на графах сons:
procedure Verify(P) // Главная процедура: берет на вход программу P и запускает вспомогательную процедуру Visit
Visit(P, G0) // Visit запускается от нашей программы и пустого графа и рекурсивно исследует все соответствующие графы
procedure Visit(P, G) // описание процедуры исследование графов
if !cons G then return // если граф не удовлетворяет предикату консисетности то выходим из цикла
a := next(P, G) // выбираем какую инструкцию в программе надо исполнить следующей и записываем соответствующее событие a в G
switch a do
case a = ⊥ // если в a ничего не записалось, значит мы исполнили все инструкции
return “OK”
case a ∈ error // если а соответствует нарушению assert’а или какой-то ошибке то вернем сообщение об ошибке
exit(“error”)
… // в иных случаях мы будем хитро рекурсивно вызываться на каких-то других графахПримерно так этот алгоритм и реализован. Посмотрим, как его кодировать в Coq.
Будем говорить, что граф G1 связан отношением ⇒ с графом G2 (и писать G1 ⇒ G2) если Visit(P, G1) вызовет Visit(P, G2) на верхнем уровне рекурсии. Далее введем некоторые обозначения:
G1 ⇒k G2 будет значить, что G1 ⇒ ..k раз... ⇒ G2
G1 ⇒* G2 будет значить, что существует некоторый k такой, что G1 ⇒k G2
О том, что я проверил на Coq
Корректность
Theorem TruSt_Correct : forall G, G0 ⇒* G -> cons G
Эта теорема говорит о том, что если мы за какое-то количество шагов можем дойти из начального графа в граф G, то граф G является консистентным. Эта теорема доказывается тривиально, так как алгоритм явно на каждом шаге проверяет графы на консистентность.
Терминируемость
Theorem TruSt_Terminate : exists B, forall G, G0 ⇒k G -> k < B
Есть некоторая оценка на количество вложенных вызовов рекурсии алгоритма. Тут надо пояснить, что весь этот метод работает только для конечных программ. То есть это должны быть программы без бесконечных циклов и рекурсий (если в нашей программе есть потенциально бесконечный цикл, то мы просто разворачиваем его на наперед заданную глубину и верификация происходит по модулю этой глубины). Далее можно доказать, что есть некоторые события, которые никогда не удаляются (а только добавляются) в ходе рекурсивных вызовов алгоритма. Из этого легко следует терминируемость.
Полнота
Theorem TruSt_Complete : forall G, cons G /\ p_sem G -> G0 ⇒* G
Тут написано, что если
cons G— граф G консистентенp
_sem G— граф G кодирует некоторое исполнение нашей программы,
то мы этот граф встретим на каком-то рекурсивном вызове. То есть эта теорема гарантирует, что мы точно проверим все возможные исходы.
Это одна из самых сложных теорем. Для ее доказательства пришлось построить обратный алгоритм для Visit: Prev. То есть Prev каждому консистентному графу (относительно cons) сопоставляет его непосредственного предка относительно ⇒ (если он существует). Prev получается записать намного проще, чем Visit, более того, он будет детерминированным, так что доказывать теоремы для него проще. Далее показываются две вещи:
если
Prev G = G’, тоG’ ⇒ Gесли
cons Gиp_sem G, то последовательно применяяPrevкGмы всегда придем к пустому графу.
Из этого легко следует теорема.
Оптимальность
В Coq ее сформулировать не очень просто, поэтому покажу схематично. Пусть
G0 ⇒ G1 ⇒ G2 ⇒ … ⇒ Gnесть последовательность шагов из пустого графа в некоторый GnG0 ⇒ H1 ⇒ H2 ⇒ … ⇒ Hnесть последовательность шагов из пустого графа в некоторый Hn иHn = Gn
Тогда и все промежуточные графы тоже будут равны. То есть мы не посетим один и тот же граф два раза.
Эта теорема тоже очень непростая и следует из того, что обратная процедура к Visit детерминирована.
Итоги
В итоге я проверил на Coq полный набор теорем про корректность представленного алгоритма. В ходе этой проверки было:
Найдена куча ошибок и неточностей в доказательствах на бумажке. Некоторые леммы не доказывались в том виде, в котором они были сформулированы, и пришлось придумывать новые формулировки.
Некоторые теоремы (например, теорема об оптимальности) были переформулированы, чтоб точнее ухватить суть вещи, которую мы хотим доказать.
Также в ходе формализации я заметил, что одно место в алгоритме является избыточным, и его убрали. Если вкратце, то в этом месте делалась проверка, которая следовала из других проверок. Так как на корректность алгоритма это не влияло, то понять, что оно лишнее, было непросто. Я заметил, что в доказательствах оно не играет роли, и предложил его убрать.
Заключение
В этом проекте мне пришлось во многом выйти из своей зоны комфорта: я писал его на новом для себя диалекте языка Coq, общался с людьми на английском, пользовался GitLab’ом и т.д... Это однозначно ценный опыт, но самое главное, что мне удалось поработать с мега крутыми специалистами в области Weak Memory. Надеюсь, что я смогу продолжить сотрудничать с ними в будущем. Это была очень крутая стажировка!
Мой код на GitHub