Блез Паскаль - один из основателей математического анализа, блестящий физик и философ. С ранних лет он проявлял недюжинные способности во всех областях науки и техники, за которые брался его пытливый ум. Например, в возрасте 8 лет Блез, даже не зная толком названий геометрических фигур (окружность он называл "колечком", а прямую - "палочкой"), доказал 32-ю теорему Евклида о сумме углов треугольника.

Неудивительно, что в 16-летнем возрасте юный гений стал доказывать уже свои теоремы. С одной из таких теорем я бы хотел Вас познакомить. Доказательство теоремы не тривиально (доказательство для жаждущих), поэтому я просто хочу показать каждому красоту геометрии. Начнем с простого предварительного построения:
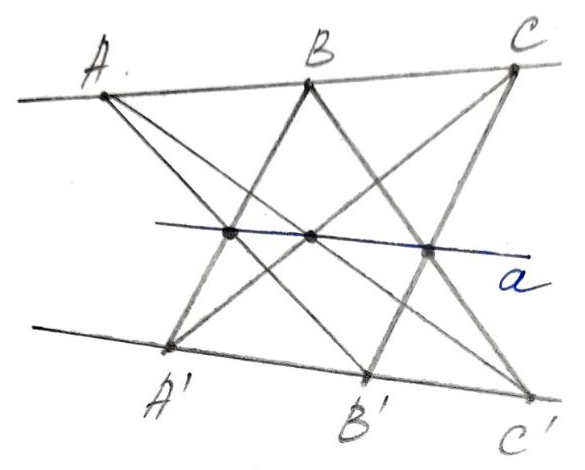
Мы взяли две непараллельные прямые, отметили три пары точек (произвольных в известной степени), а затем соединили каждую точку с её противоположными собратьями. О чудо! Все три точки пересечения лежат на одной прямой! Паскаль пошел дальше своего предшественника: "А что, если попробовать сделать то же самое с окружностью?"

А что, если пойти дальше? Ведь окружность - это частный случай эллипса, который, в свою очередь, является одним из трех главных типов т.н. конических сечений:

К коническим сечениям относятся: парабола, эллипс и гипербола + три вырожденных случая - точка, прямая и пара прямых. Именно такую форму принимает пересечение плоскости с поверхностью кругового конуса. Как Вы уже догадываетесь, для параболы результат оказался таким же:
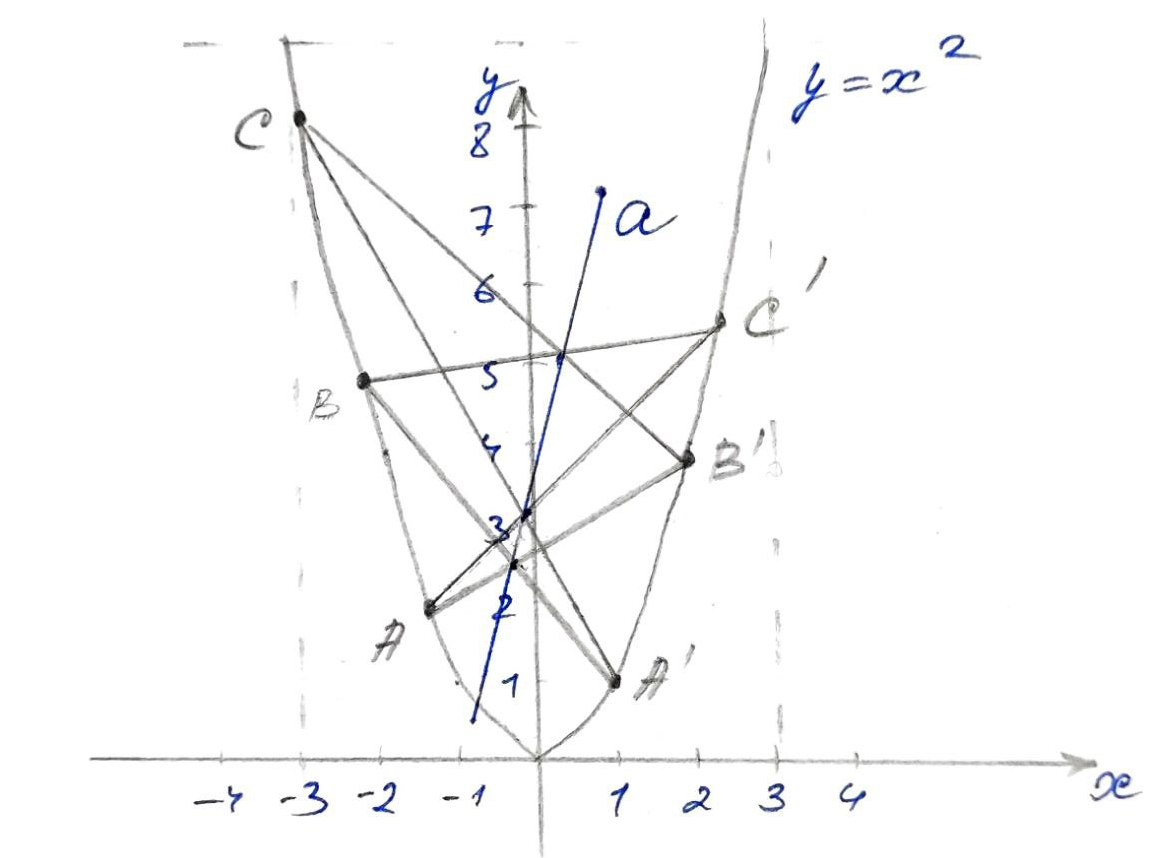
Такого рода построения позволили сформулировать 16-летнему мальчику первую из теорем, названных его именем:
"Если шестиугольник вписан в коническое сечение, то точки пересечения трех пар противоположных сторон лежат на одной прямой".
Современники настолько были поражены теоремой Паскаля, что на латинице она известна как "Hexagrammum Misticum":
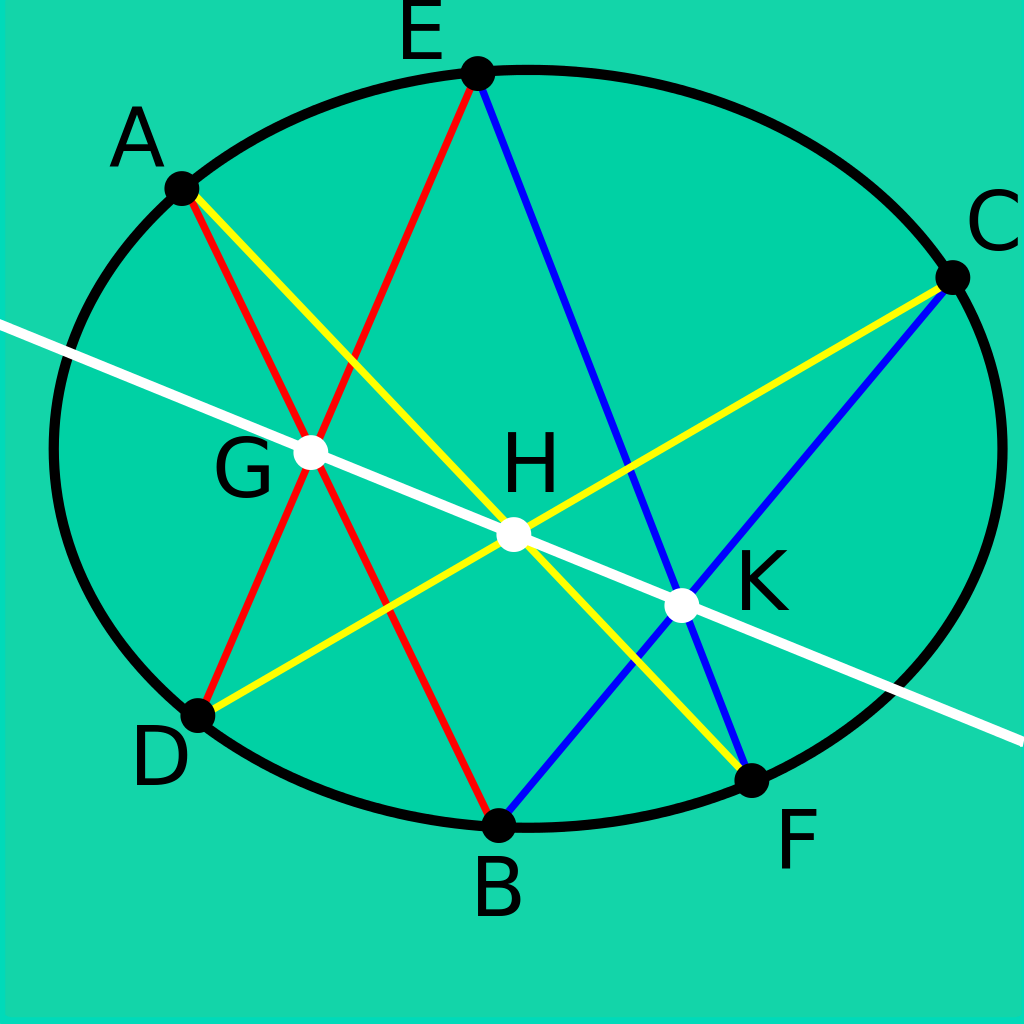
Информация об этой теореме вместе с более чем (!!!) 400 следствиями вошла в "Полный труд о конических сечениях", написанный Паскалем в 31 год. Восхищения этой уникальной рукописью уже после смерти гения не скрывал сам Готфрид Лейбниц, но, к сожалению, работа была утеряна племянником Паскаля и так и не была опубликована.
Хотя имеется множество вариантов доказательства теоремы Паскаля, историкам математики не известно, как она была доказана в первоисточнике, хотя многие и сходятся к использованию теоремы Менелая.










