
Казалось бы, жизнь невозможно повернуть назад, а предмет из фотографии не восстановишь. Хотя с последним можно поспорить: из плоского 2D-изображения реально восстановить 3D-модель объекта. Подобная «магия» часто практикуется в AR/VR, управлении беспилотниками и других сферах. Для этого первым делом производится калибровка камеры. Чтобы понять процесс калибровки, сперва следует освоить базовые принципы преобразования трехмерных координат точек в двухмерные на плоскости.
Сегодня мы рассмотрим:
геометрию формирования изображения на сенсоре камеры (pinhole модель);
как рассчитываются координаты точки на сенсоре для точки из реального мира;
как переходить от одной системы координат к другой;
что такое внутренние и внешние параметры камеры и зачем они нужны.
Начнем с основ геометрии формирования изображения, для чего в лучших традициях математических задачек из учебников поупражняемся на яблоках, точнее — одном яблоке. Представим, что оно лежит где-нибудь посреди комнаты. Берем камеру, чтобы сфотографировать яблоко. Итак, нам дан объект в трехмерной системе координат мирового пространства, который мы хотим запечатлеть в двухмерной среде.
Основная задача здесь — поиск координат пикселей на фотографии с камеры. Они соответствуют трехмерным координатам центра яблока в 3D пространстве. А вот здесь уже стоит поговорить о четырех различных системах координат, каждая из которых играет важную роль в описании пространства и объектов.
Мировая система координат
Это глобальная точка отсчета, которая помогает определить положение предмета в трехмерном пространстве. Она служит стандартом для измерения и описания координат объектов независимо от точки наблюдения.
Возвращаясь к примеру, мировая система координат находит позицию яблока в пространстве комнаты независимо от того, где именно расположилась камера. На помощь в этом приходят те самые числа , которые фиксируют положение объекта вдоль трех взаимно перпендикулярных осей (Декартова система координат). Это горизонтальная ось
, вертикальная
и глубина
.
На рисунке ниже желтым цветом показана мировая система координат:
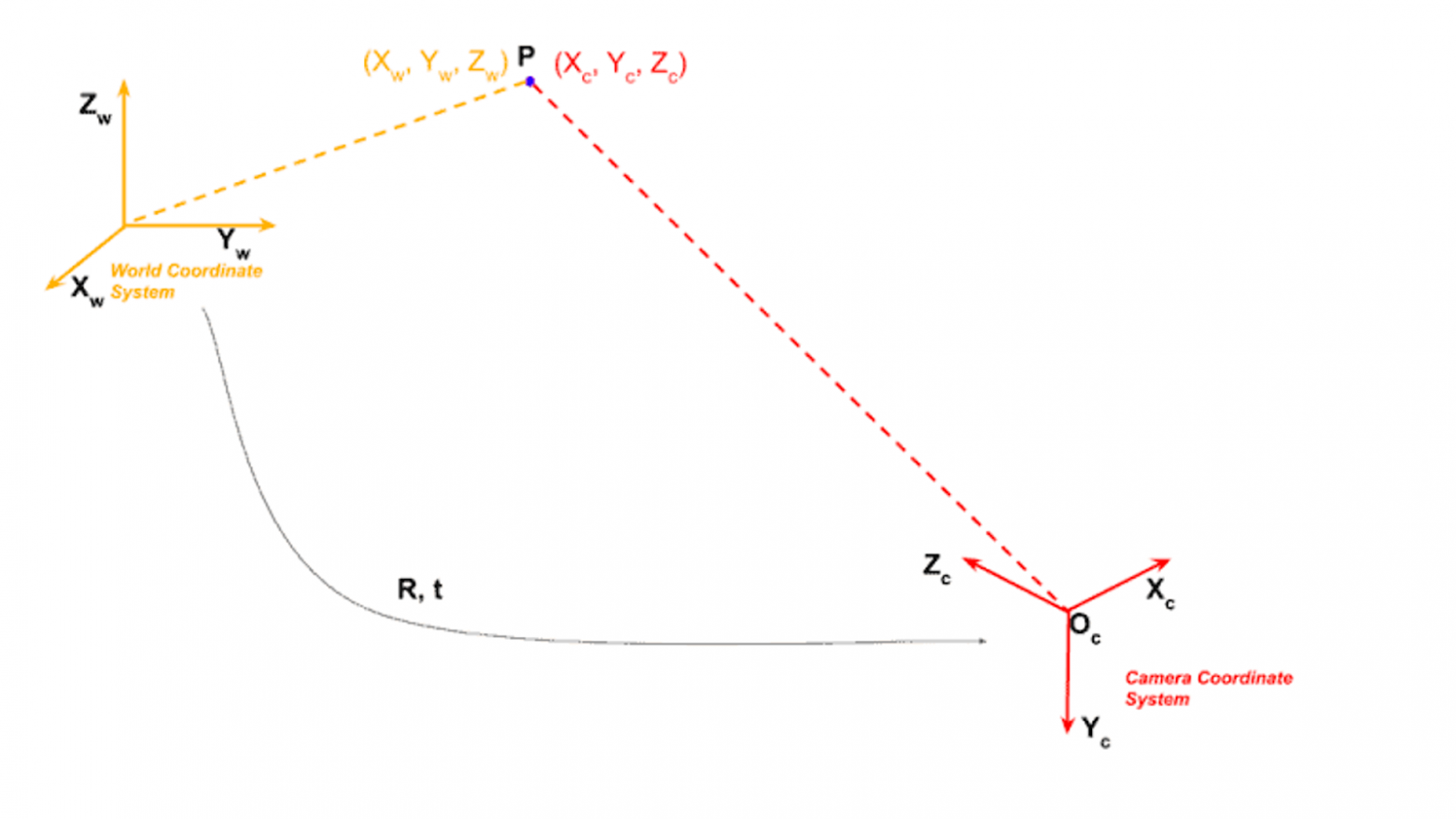
Начальную точку координат можно выбрать в любом пункте комнаты, например, в одном из углов. Тогда оси
и
будут ориентированы в горизонтальной плоскости вдоль двух стен, в то время как ось
— вдоль вертикального угла стены.
Чтобы вычислить положение яблока, необходимо измерить расстояние от начала координат в мировой системе до объекта. В итоге мы получим
Система координат камеры
Теперь представим, что камеру установили в начале координат комнаты и настроили так, что оси совпадают с соответствующими осями
помещения. То есть две системы координат сливаются воедино и становятся эквивалентными друг другу.
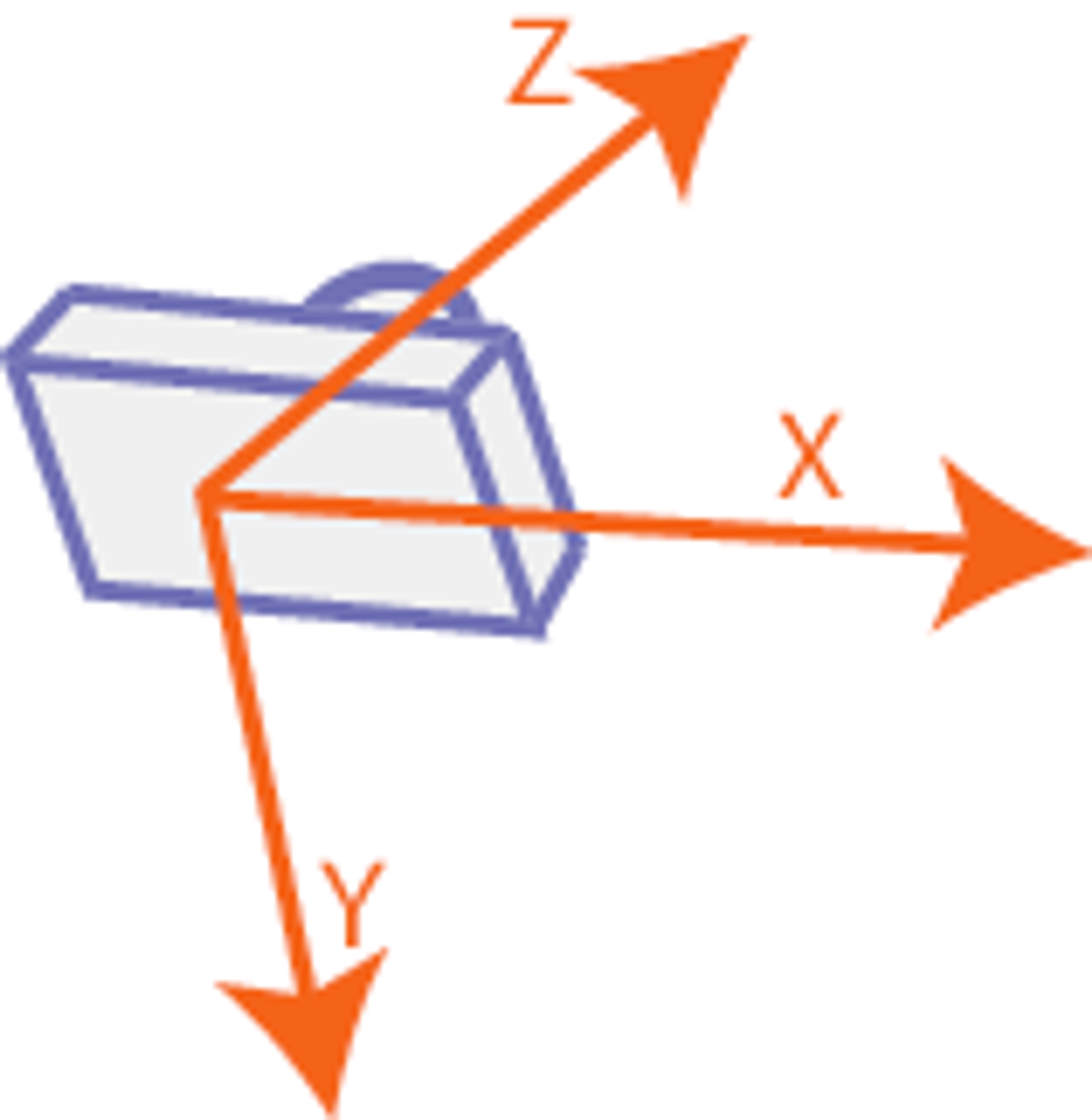
Но нам важно иметь возможность поставить камеру в любой точке комнаты, из которой можно наблюдать за нужной областью. Для этого-то и ищут связь между 3D координатами мира и 3D координатами камеры.
Чаще всего расположение осей камеры выглядит следующим образом:
Мировые координаты и координаты камеры связаны матрицей вращения и вектором перемещения
.
— матрица поворота размером 3x3. Она описывает ориентацию камеры, с помощью которой мы выравниваем направления осей мировой системы координат и системы координат камеры.
— вектор параллельного переноса размером 3x1. Он определяет положение центра камеры, с помощью которого мы смещаем начало координат в мировом пространстве в начало координат в матрице камеры.
Соответственно, у нашего яблока будут значения координат в мировой и
— в системе камеры. Используя приведенную ниже формулу, можно перевести координаты точек из одной системы в другую.
Однородные координаты
Это концепция применяется в геометрии и компьютерной графике для представления точек, векторов и преобразований в более простой и обобщенной форме. Однородные координаты позволяют легко выполнять различные геометрические преобразования путем умножения матриц (например, трансляцию, масштабирование и поворот). Главное удобство в том, что все можно выразить линейной операцией. В однородных координатах точка в трехмерном пространстве представляется четырьмя числами , где
является весовым коэффициентом. В декартовых координатах она соответствует точке:
Например, для плоскости мы задаем каждую точку парой координат Чтобы перевести ее в однородные координаты, добавляется ещё одна координата
Отсюда мы получаем следующие свойства:
Точке
будет соответствовать однородная координата
При умножении на любое число координаты будут задавать ту же точку.
Например, точка в однородных координатах будет
, и при умножении на 5 будет
, но она всё равно задаёт ту же точку
, и таких примеров бесконечное множество.
То же самое работает и для трехмерного пространства. Для нас наиболее интересно представлять точку с единичной глубиной, то есть . Поэтому для однородных координат
мы можем разделить все координаты на
и получить
, что равно
Что такое однородные координаты, в общих чертах обрисовали. Теперь воспользуемся их свойствами для получения универсальных координат на изображении. Разделим на глубину и подвинем изображение на единичное расстояние от центра проекции. В результате мы получаем точку на изображении
После этого можно использовать свойства однородных координат, отбросить
и прийти к
Таким образом, получается компактно представить данные в более простой реализации и объединить несколько преобразований в одно.
Модель камеры с точечной диафрагмой
Жаль разрывать рассказ о четырех системах координат на полуслове, но чтобы лучше понять последнюю из них, придется сделать небольшое отступление. Отдохнем от формул и посмотрим на девайс, который позволяет применить все эти расчеты на практике. Одно из самых простых оптических устройств для получения изображения — пинхол-камера. Понял принцип ее работы — считай, постиг основы основ фотографии.
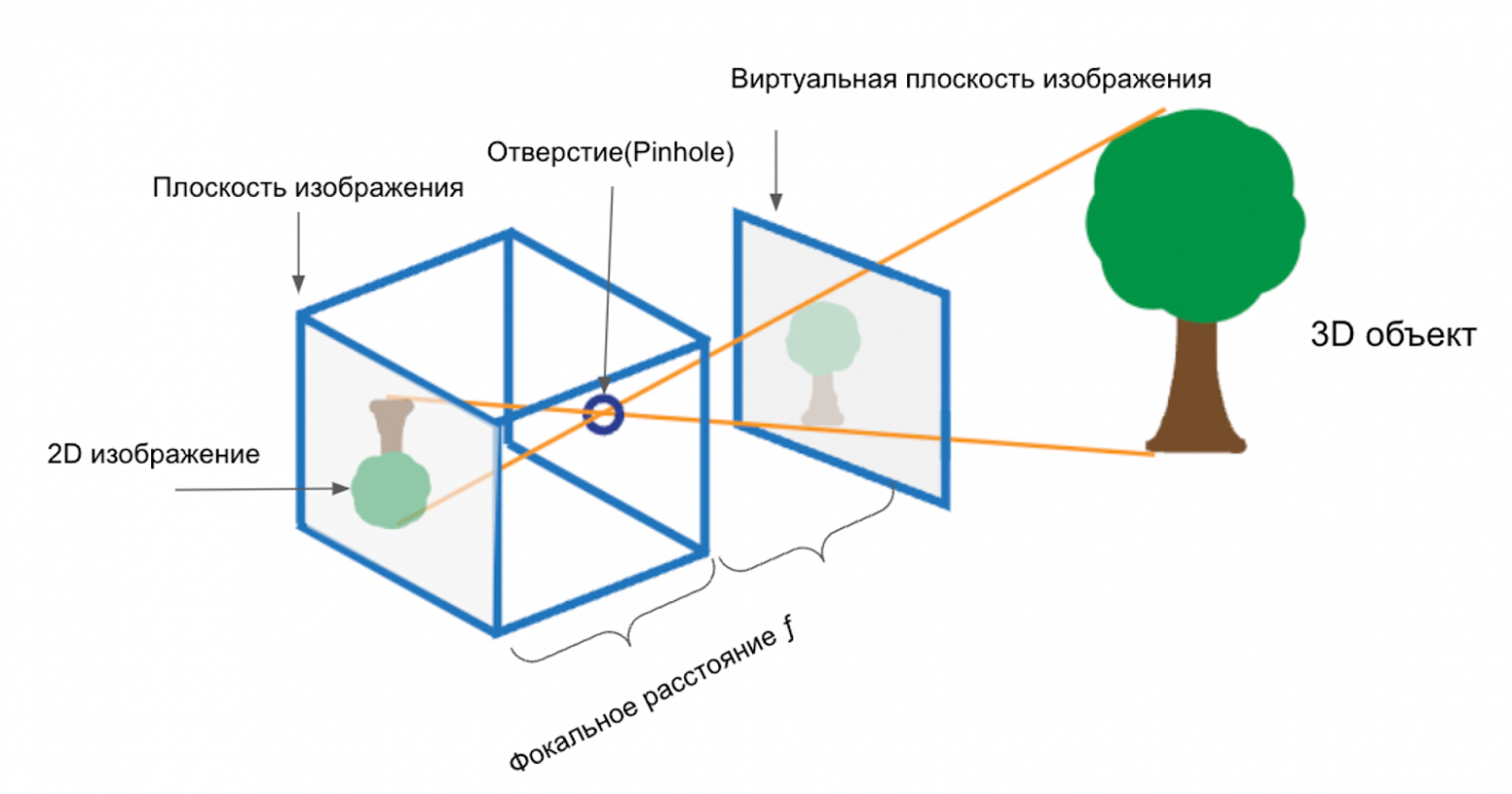
Такая камера пропускает свет через небольшое отверстие (пинхол) и фокусирует его на противоположную внутреннюю стенку, служащую экраном (так называемая «плоскость изображения»). В нашем случае это матрица камеры (сенсор). На ней формируется 2D изображение внешнего мира. Картинка получается перевернутой вверх ногами и отраженной слева направо, поскольку свет распространяется по прямым линиям
Важную роль играет промежуток между pinhole и плоскостью изображения, который называется фокусным расстоянием . Оно зависит от размеров камеры и отверстия, а также от оптических свойств пинхола. Чем больше фокусное расстояние, тем четче и одновременно мельче по размеру будет проекция.
Притом для упрощения работы и анализа часто используется концепция виртуальной плоскости изображения. Она размещается на расстоянии перед отверстием и служит для формирования такой же картинки, как на сенсоре, но уже без перевернутого представления.
Если вы хотите не просто прочитать об этом, но и увидеть все в действии, то здесь можно поиграть с простой моделью pinhole-камеры. Вы досконально рассмотрите 2D изображения при изменении размера диафрагмы и количества света.
Система координат изображения
Теперь мы знаем, что такое фокусное расстояние и с чем его едят и готовы идти дальше. Представим, что мы получили точку с координатами . Далее ее можно спроецировать на плоскость изображения.
Координаты точки на изображении сильно зависят от расстояния оптического центра, или центра проекции .
Плоскость изображения размещается на фокусном расстоянии от оптического центра
.
Последний обозначает точку внутри камеры, через которую проходит главная оптическая ось от фокусного объектива к сенсору (или матрице) камеры.
Во время формирования изображения на плоскости матрицы оптический центр определяет точку
, в которой линии проекции из объектива пересекаются и создают точное представление трехмерных объектов на двумерной поверхности.
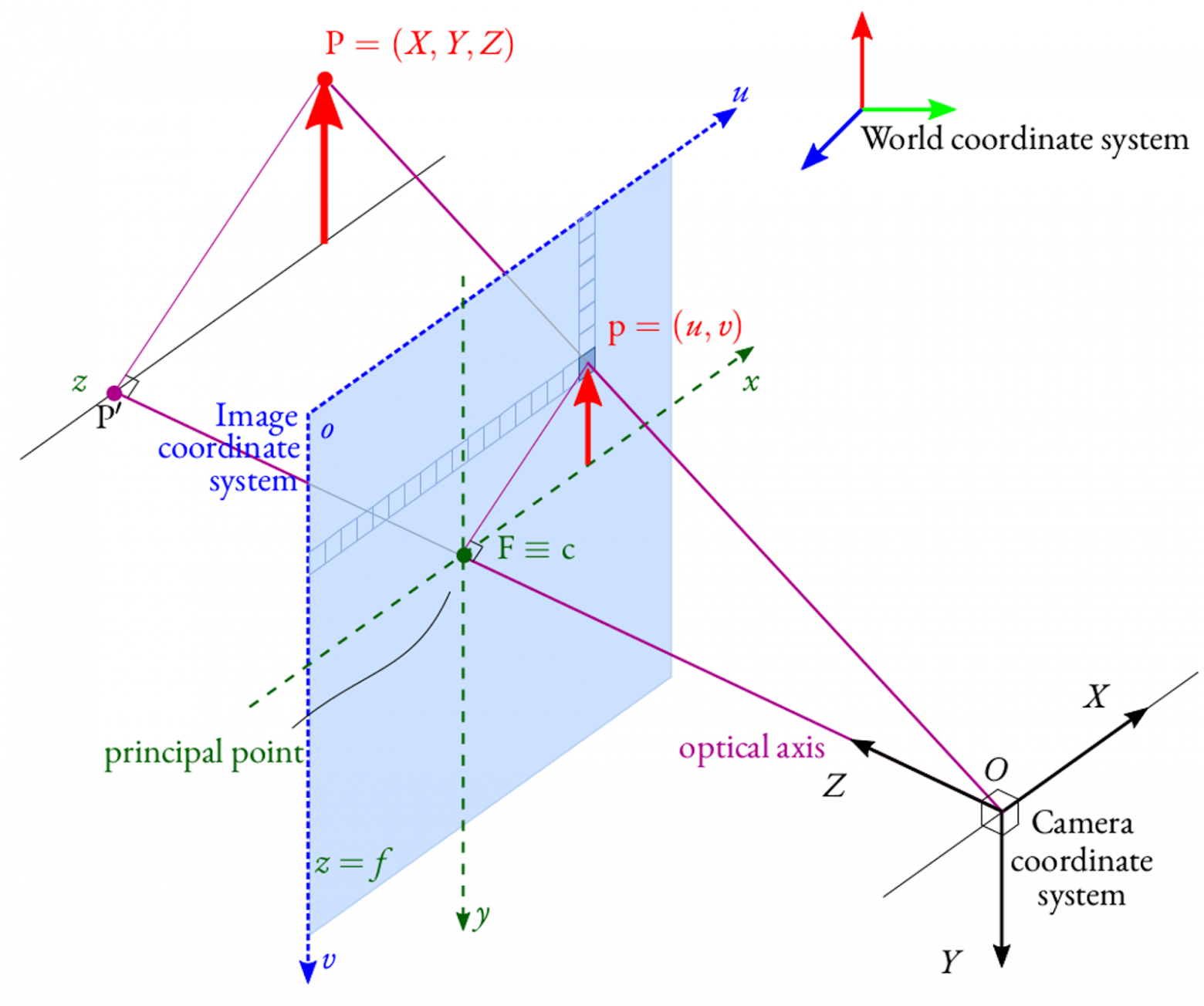
Точки на плоскости изображения и
в 3D координатах камеры эквивалентны:
Это означает, что точка на плоскости изображения соответствует точке
в трехмерном пространстве. Между их координатами есть определенное отношение, а именно — принадлежности к одному лучу, где
— константа:
Такое отношение остается постоянным для всех точек, расположенных на одной линии проекции точки на плоскость изображения. Оно позволяет установить связь между 2D координатами на изображении и 3D координатами объектов в пространстве.
Из проекции треугольников и
на плоскости
и
соответственно мы получаем:
где — координаты на изображении,
(
на рисунке 3) — фокусное расстояние,
— координаты точки в системе координат камеры.
Формулы выше можно получить и в матричном виде:
Принцип подобия треугольников связывает однородные и декартовы координаты, поэтому мы можем записать формулу так:
Матрица 3x3 в формуле выше — это внутренние параметры камеры.
Важно, что матрица сейчас не учитывает положение главной точки
(principal point), ориентацию осей
и
, а также размеры пикселей камеры, которые влияют на фокусное расстояние. Поэтому далее мы рассмотрим изменение матрицы
в более реалистичных условиях.
Матрица показывает одинаковое фокусное расстояние при условии квадратного пикселя на матрице камеры. Так происходит не всегда, поэтому матрица с двумя разными фокусными расстояниями будет выглядеть следующим образом:
Оптический центр и ось
камеры должны пересекаться в начале координат изображения в точке
(principle point). Однако бывают исключения,например, если сдвинулся сенсор или произошло искажение при перемещении объектива. Возможен и небольшой перекос
между осями
и
датчика камеры.
Ранее мы получили калибровочную матрицу, или матрицу внутренних параметров камеры (intrinsic matrix). С ее помощью у нас получится следующее выражение:
Пока что на этом с общей теорией закончим. Если у вас возникли какие-то вопросы, буду рад ответить на них в комментариях. В следующей публикации мы рассмотрим уже непосредственно калибровку камеры, сбор датасета, различные виды маркеров и проблему дисторсии.
P.S.
Первая версия статьи написана для deepschool-pro, на Хабре публикуется с изменениями и дополнениями.