AlexAproner 2 ноя 2023 в 17:47

Ещё раз про алгоритм сжатия Хаффмана

Сложный

21 мин

18K

Блог компании SamsungАлгоритмы*Математика*Сжатие данных*

Туториал

К написанию этой заметки меня сподвигло почти полное отсутствие информации на русском языке относительно эффективной реализации алгоритма оптимального префиксного кодирования алфавита с минимальной избыточностью, известного по имени своего создателя как алгоритм Хаффмана. Этот алгоритм в том или ином виде используется во многих стандартах и программах сжатия разнообразных данных.

Канонический алгоритм Хаффмана

Хорошее описание алгоритма Хаффмана можно найти в книгах [1,2]. Поэтому я почти дословно процитирую информацию из раздела, посвящённого описанию алгоритма Хаффмана в книге [1].

Алгоритм относится к группе “жадных” (greedy) алгоритмов и использует только частоту появления одинаковых символов во входном блоке данных. Ставит в соответствие символам входного потока, которые встречаются чаще, цепочку битов меньшей длины. И напротив, встречающимся редко - цепочку большей длины. Для сбора статистики требует двух проходов по входному блоку (также существуют однопроходные адаптивные варианты алгоритма).

Характеристики алгоритма Хаффмана [1]:

Степени сжатия: 8, 1.5, 1 (лучшая, средняя, худшая степени)
Симметричность по времени: 2:1 (за счёт того, что требует двух проходов по массиву сжимаемых данных)
Характерные особенности: один из немногих алгоритмов, который не увеличивает размера исходных данных в худшем случае (если не считать необходимости хранить таблицу перекодировки вместе с файлом).

Основные этапы алгоритма сжатия с помощью кодов Хаффмана

Сбор статистической информации для последующего построения таблиц кодов переменной длины
Построение кодов переменной длины на основании собранной статистической информации
Кодирование (сжатие) данных с использованием построенных кодов

Описанный выше алгоритм сжатия требует хранения и передачи вместе c кодированными данными дополнительной информации, которая позволяет однозначно восстановить таблицу соответствия кодируемых символов и кодирующих битовых цепочек.

Следует отметить, что в некоторых случаях можно использовать постоянную таблицу (или набор таблиц), которые заранее известны как при кодировании, так и при декодировании. Или же строить таблицу адаптивно в процессе сжатия и восстановления. В этих случаях хранение и передача дополнительной информации не требуется, а также отпадает необходимость в предварительном сборе статистической информации (этап 1).

В дальнейшем мы будем рассматривать только двухпроходную схему с явной передачей дополнительной информации о таблице соответствия кодируемых символов и кодирующих битовых цепочек.

Первый проход по данным: сбор статистической информации

Будем считать, что входные символы - это байты. Тогда сбор статистической информации будет заключаться в подсчёте числа появлений одинаковых байтов во входном блоке данных.

Построение кодов переменной длины на основании собранной статистической информации

Алгоритм Хаффмана основывается на создании двоичного дерева [3].

Изначально все узлы считаются листьями (конечными узлами), которые представляют символ (в нашем случае байт) и число его появлений. Для построения двоичного дерева используется очередь с приоритетами, где узлу с наименьшей частотой присваивается наивысший приоритет.

Алгоритм будет включать в себя следующие шаги:

Шаг 1. Помещаем все листья с ненулевым числом появлений в очередь с приоритетами (упорядочиваем все листья в порядке убывания числа появления)

Шаг 2. Пока в очереди больше одного узла, выполняем следующие действия:

Шаг 2a. Удаляем из очереди два узла с наивысшим приоритетом (самыми низкими числами появлений)

Шаг 2b. Создаём новый узел, для которого выбранные на шаге 2a узлы являются наследниками. При этом число появлений нового узла (его вес) полагается равным сумме появлений выбранных на шаге 2a узлов

Шаг 2c. Добавляем узел, созданный на шаге 2b, в очередь с приоритетами.

Единственный узел, который останется в очереди с приоритетами в конце работы алгоритма, будет корневым для построенного двоичного дерева.

Чтобы восстановить кодирующие слова, нам необходимо пройти по рёбрам от корневого узла получившегося дерева до каждого листа. При этом каждому ребру присваивается бит “1”, если ребро находится слева, и “0” - если справа (или наоборот).

Пример работы описанного выше алгоритма представлен на рисунке 1.

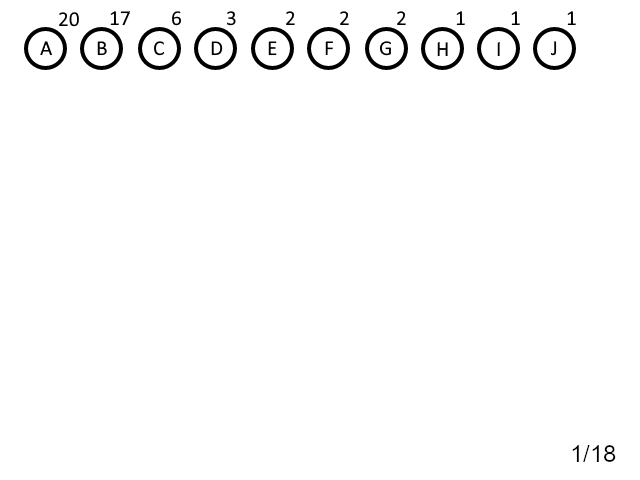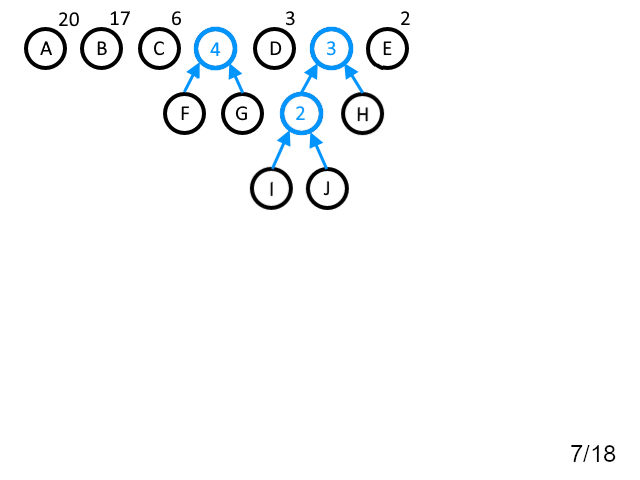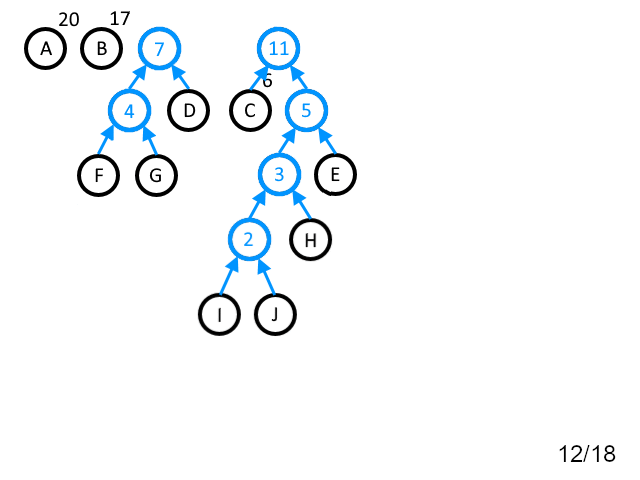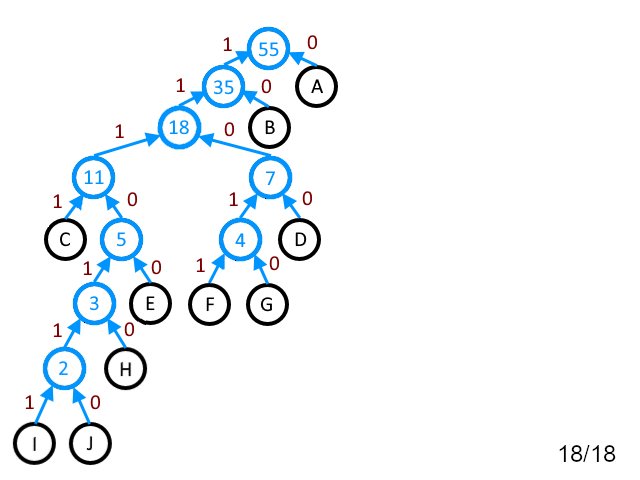
Рисунок 1. Пример работы алгоритма Хаффмана

Таблица 1. Построенные коды Хаффмана для примера, приведённого на рисунке 1.

Входной символ	Число появлений	Длина битового кода	Битовый код
"A"	20	1	0
"B"	17	2	10
"C"	6	4	1111
"D"	3	4	1100
"E"	2	5	11100
"F"	2	5	11011
"G"	2	5	11010
"H"	1	6	111010
"I"	1	7	1110111
"J"	1	7	1110110

Приведённое выше описание алгоритма создаёт впечатление, что реализация алгоритма построения кодов должна быть основана на указателях и требовать дополнительной памяти для хранения адресов внутренних узлов двоичного дерева. Пример такой реализации можно найти, например, в статье [3]. Для целей обучения такая реализация хороша, но и только. И становится очень печально, когда на полном серьёзе такую реализацию пытаются использовать в реальном ПО.

Построение кодов с минимальной избыточностью, эффективно использующее оперативную память

Основные идеи алгоритма

Прежде чем перейти к описанию такого эффективного алгоритма построения кодов с минимальной избыточностью, нам придётся немного погрузится в теорию кодирования [4].

До этого момента мы подразумевали, что результатом построения кодов является назначение каждому входному символу битового кода. Соответствие битовых кодов каждому входному символу задаёт схему кодирования.

Чтобы кодирование было взаимно-однозначным, схема кодирования должна обладать свойством префикса – т.е. ни один используемый для кодирования определённого символа битовый код не должен быть префиксом битового кода, предназначенного для кодирования любого другого входного символа [1].

Пусть – длина битового кода, предназначенного для кодирования -го символа из алфавита входных символов. Тогда необходимым условием того, что схема кодирования обладает свойством префикса, является выполнение следующего неравенства:

$K = \sum_{i=1}^{n} 2^{-l_i} \leq 1$

Это неравенство в литературе называется неравенством Макмиллана-Крафта (Kraft inequality) [4,5].

В то же время, чтобы схема кодирования обладала свойством минимальной избыточности, необходимо построить такие битовые коды, чтобы математическое ожидание длины битовых кодов $l_{avg} = \sum_{i=1}^{n}l_i*p_i$ было минимальным (- вероятности появления символов входного алфавита).

Необходимо ещё раз отметить, что схема кодирования, задающая множество битовых кодов с длинами, для которых выполняется неравенство Макмиллана-Крафта, не гарантирует свойство префикса. Так, для схемы кодирования двухсимвольного алфавита, состоящей из битовых кодов “0” и “00”, неравенство Макмиллана-Крафта будет выполняться: $K = 2^{-1} + 2^{-2} = 0.75 \leq 1$ . Но битовые коды очевидно не будут обладать свойством префикса. Тем не менее, если у нас есть информация о длинах кодов , для которых выполняется неравенство Макмиллана-Крафта, мы всегда можем построить соответствующие этим длинам битовые коды, которые будут обладать свойством префикса [4,5].

К алгоритму построения битовых кодов по их длинам мы вернёмся позднее, а сейчас зафиксируем тот факт, что задача построения кодов с минимальной избыточностью сводится к нахождению длин таких кодов для символов входного алфавита на основе собранной статистической информации.

Следуя статье [6], опишем алгоритм построения кодов с минимальной избыточностью, не требующий для своей работы дополнительной памяти (“in-place”).

Прежде всего рассмотрим основные идеи алгоритма. В его основе лежат следующие два наблюдения.

Первое наблюдение: мы можем хранить листья двоичного дерева отдельно от внутренних узлов, которые формируются в процессе слияния (шаги 2a и 2b) описанного выше алгоритма Хаффмана. Таким образом у нас получается две очереди с приоритетами. Более того, поскольку внутренние узлы формируются в отсортированном порядке, а листья также сортируются на шаге 1, то очереди с приоритетами превращаются в обычные списки.

При этом вес любого узла дерева необходим только до того момента пока узел не будет обработан. Для любого заданного слияния необходимо хранить по крайней мере весов. В конце слияний у нас сохранится лишь один вес.

Второе наблюдение: нам нет необходимости хранить указатели на родительские узлы (индексы родительских узлов) в двух списках. Если глубина каждого внутреннего узла известна, то мы можем восстановить глубину для каждого из листьев (так как можно предположить, что длины кодов не будут возрастать). Например, для дерева, изображённого на рисунке 2, с глубинами внутренних узлов (обозначенных оранжевым цветом) [3, 3, 2, 1, 0] глубины листьев (обозначенных зелёным цветом) будут равны [4, 4, 4, 4, 2, 1].

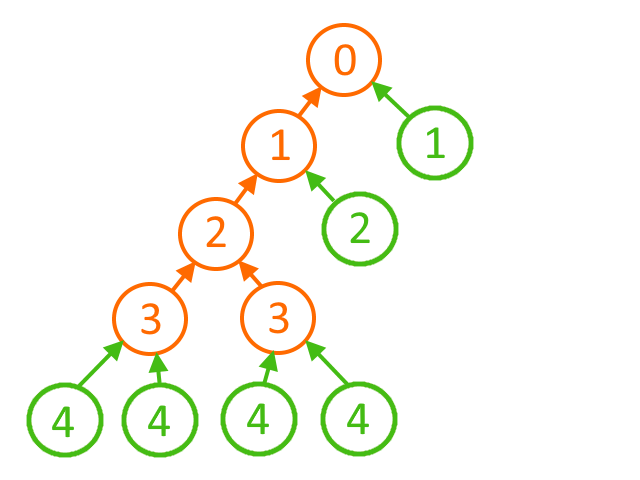
Рисунок 2. Пример дерева с глубинами

В начале процесса слияния ни в одном из списков нет указателей на родительские узлы (индексов родительских узлов). А в конце процесса слияния у нас будет указателей на родительские узлы (индексов родительских узлов). Но все эти указатели (индексы) будут принадлежать внутренним узлам.

Общее число весов (хранящихся для узлов, которые не были ещё обработаны) и указателей на родительские узлы (индексов родительских узлов) (хранящихся для внутренних узлов, которые уже были обработаны) никогда не превысит . Т.е. указатели на родительские узлы (индексы родительских узлов) и веса могут храниться во входном массиве .

Таким образом, входной массив одновременно является рабочим для алгоритма. В начале работы алгоритма массив содержит числа (частоты) появлений символов входного алфавита, состоящего из символов, во входном потоке данных. Затем на каждом из этапов содержимое массива изменяется: элементы в массиве на разных этапах алгоритма используются для хранения числа (частоты появлений) символов, весов внутренних узлов, индексов родительских узлов, глубин внутренних узлов, и наконец, глубины листьев (длины кодов для каждого символа).

Основные этапы алгоритма

Перейдём к непосредственному описанию алгоритма “inplace” построения кодов с минимальной избыточностью.

Этот алгоритм включает в себя следующие три основных этапа:

Этап №1. Формирование внутренних узлов.

Входные данные: массив , содержащий числа (частоты) появлений символов входного алфавита из символов.

Выходные данные: массив , содержащий следующие данные:

- указатели на родительские узлы (индексы родительских узлов);

- вес корневого узла;

- не используется.

    1   s ← 0
    2   r ← 0
    3   for t ← 0 to n-2
    4       do ⇨ выбираем первый узел-потомок
    5          if (s > n-1) or (r < t and A[r] < A[s])
    6          then ⇨ выбираем внутренний узел
    7               A[t] ← A[r]
    8               A[r] ← t+1
    9               r ← r+1
    10         else ⇨ выбираем лист
    11              A[t] ← A[s]
    12              s ← s+1
    13         ⇨ выбираем второй узел-потомок
    14         if (s > n-1) or (r < t and A[r] < A[s])
    15         then ⇨ выбираем внутренний узел
    16              A[t] ← A[t]+A[r]
    17              A[r] ← t+1
    18              r ← r+1
    19         else ⇨ выбираем лист
    20              A[t] ← A[t]+A[s]
    21              s ← s+1

Важные замечания к показанному выше псевдокоду: - Операции “or” и “and” вычисляются условно (так, как это, например, происходит в языке программирования C/C++).

Суть первого этапа в следующем: на каждой итерации цикла сравнивают следующий внутренний узел с наименьшим весом (если он существует) со следующим листом с наименьшим весом (если он существует) и выбирают наименьший по весу из двух (строки 5 - 12). Найденный наименьший вес назначается вновь создаваемому узлу дерева . Затем к добавляется следующее наименьшее значение (строки 14 - 21). Если в результате на предыдущих шагах был выбран хотя бы один внутренний узел, то вес заменяется индексом родителя выбранного внутреннего узла.

Пример работы описанного первого этапа алгоритма для случая входных данных, приведённых на рисунке 1, представлен на рисунке 3.

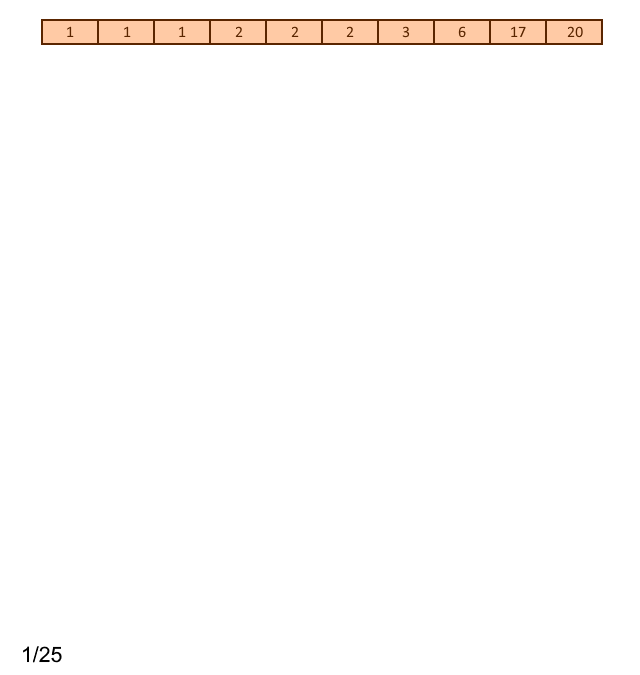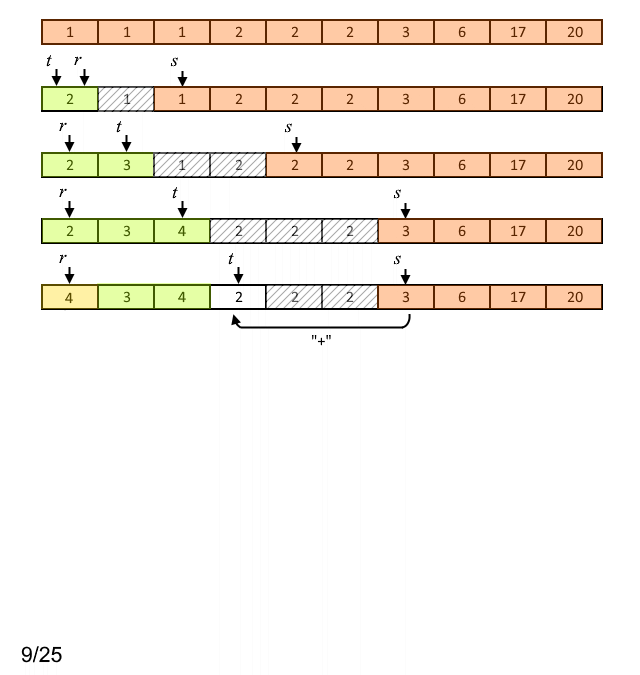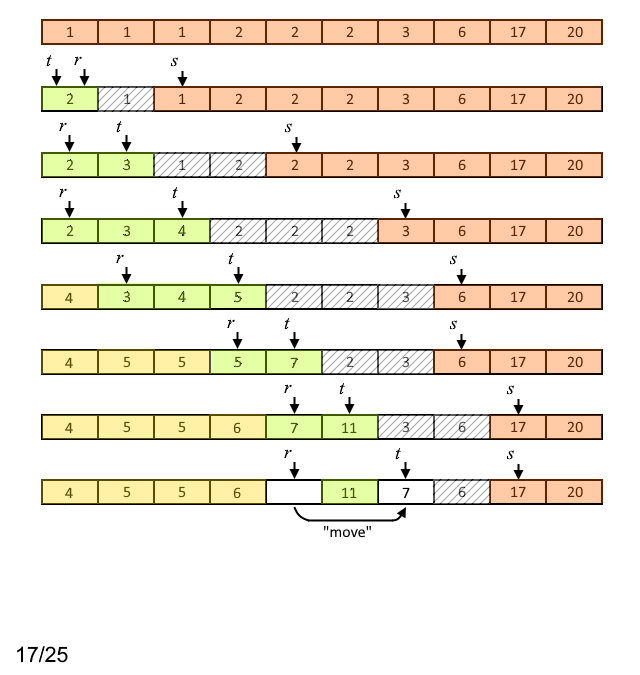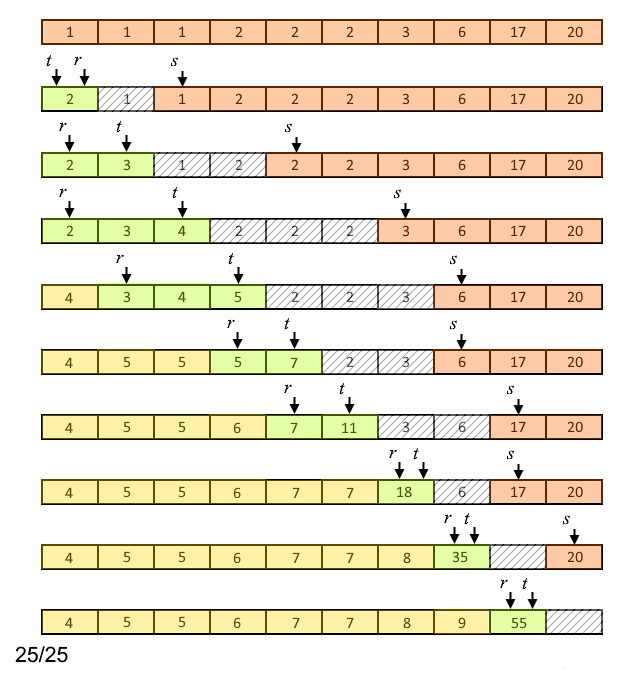
Рисунок 3. Пример работы первого этапа алгоритма

Здесь светло-коричневым цветом выделены ячейки массива, содержащие число появлений каждого символа входного алфавита; светло-зелёным - ячейки массива, содержащие веса внутренних узлов до того момента, как они будут объединены; светло-жёлтым - указатели на родительские узлы (индексы родительских узлов) после операции объединения.

Этап №2. Преобразование индексов родительских узлов в значения глубин каждого узла.

Входные данные: - указатели на родительские узлы (индексы родительских узлов);

Выходные данные: - значение глубины для каждого из внутренних узлов.

    1   A[n-2] ← 0
    2   for t ← n-2 downto 0
    3      do A[t] ← A[A[t]-1]+1

Продолжая наш пример, на этапе №2 мы получим следующий результат:

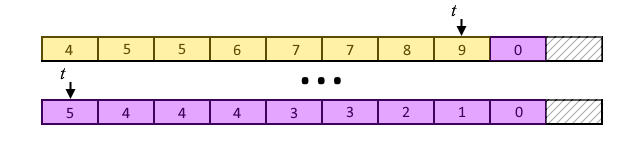
Пример преобразования индексов родительских узлов

Светло-фиолетовым выделены значения глубины для внутренних узлов.

Этап №3. Преобразование значений глубин внутренних узлов в значения глубин листьев (длин кодов).

Входные данные: - значение глубины для каждого из внутренних узлов.

Выходные данные: - значения глубины для каждого из листьев (т.е. длины кодов для каждого символа).

    1   a ← 1
    2   u ← 0
    3   d ← 0
    4   t ← n-2
    5   x ← n-1
    6   while a > 0
    7   do ⇨ определяем количество внутренних узлов с глубиной, равной d
    8      while t ≥ 0 and A[t] = d
    9         do u ← u+1
    10           t ← t-1
    11     ⇨ назначаем листьями узлы, которые не являются внутренними
    12     while a > u
    13        do A[x] ← d
    14           x ← x-1
    15           a ← a-1
    16     ⇨ переходим к следующему значению глубины
    17     a ← 2∙u
    18     d ← d+1
    19     u ← 0

глубин внутренних узлов преобразуются в глубин листьев (длин кодов для каждого символа). Для этого производится сканирование массива справа налево с использованием указателя для внутренних узлов и указателя на элемент, в котором будет сохранено значение длины кода очередного листа дерева.

Иллюстрация работы этапа №3 для нашего примера приведена на рисунке ниже:

Пример преобразования значений глубин узлов в длины кодов

Рисунок 4. Пример работы третьего этапа алгоритма

Здесь голубым цветом выделены получающиеся значения длин кодов.

Подводя итог, описанный выше алгоритм состоит из трёх этапов, на каждом из которых осуществляется проход по массиву (один раз в прямом направлении, и два - в обратном).

Алгоритм выполняется за время и использует дополнительной памяти в случае, если входной массив числа (частоты) появлений символов входного алфавита предварительно отсортирован.

Ещё раз подчеркну, что алгоритм не требует явного построения дерева с использованием указателей (дополнительного динамического выделения памяти под формируемые узлы дерева), что на практике приводит к увеличению времени, необходимого для построения кодов переменной длины.

Построение кодов переменной длины

Теперь, когда у нас есть длины кодов для каждого символа, построим для них битовые коды.

Итак, - длина битового кода, предназначенного для кодирования -го символа из алфавита входных символов. Обозначим через $n_\lambda$ число символов входного алфавита, для которых длина кода равна $\lambda$ :

$n_\lambda = | \{ i | l_i =\lambda \}, 1 \leq \lambda \leq L$

Здесь - получившаяся после применения описанного выше алгоритма максимальная длина кода.

Далее, код с длиной $\lambda$ для -го символа из множества символов, для которых длина кода одинакова и равна $\lambda$ , может быть получен с помощью следующей формулы:

$j+base[\lambda], 0 \leq j < n_\lambda,$

где

$base[\lambda]=\lceil \frac{ \sum_{k=\lambda+1}^{L} n_k*2^{L-k} }{2^{L-\lambda}} \rceil.$

Входные данные: массив , содержащий длины кодов для каждого символа входного алфавита из символов.

Выходные данные: массив , где целое число $B[i], 0 \leq i < n$ содержит битовое представление кода в -ых младших битах.

    1    ⇨ подсчитываем число символов с одинаковыми длинами кодов
    2   for i ← 0 to n-1
    3       do m[i] ← 0
    4   for i ← 0 to n-1
    5       do m[A[i]] ← m[A[i]] + 1
    6    ⇨ вычисляем значения base для каждой длины кода
    7   s ← 0
    7   for k ← L downto 1
    8       do Base[k] ← s >> (L - k)
    9          s ← s + (m[k] << (L - k))
    10   ⇨ вычисляем коды для каждого символа входного алфавита
    11  p ← 0
    12  for i ← 0 to n-1
    13     do if p ≠ A[i]
    14        then j ← 0
    15             p ← A[i]
    16        B[i] ← j + Base[A[i]]
    17        j ← j + 1

Построим коды переменной длины для нашего примера.

Таблица 2. Пример построения кодов переменной длины.

Входной символ	Длина битового кода	base	j	Битовый код
"H"	6	0	0	000000
"I"	6		1	000001
"J"	5	1	0	00001
"E"	5		1	00010
"F"	5		2	00011
"G"	5		3	00100
"D"	5		4	00101
"C"	4	3	0	0011
"B"	2	1	0	01
"A"	1	1	0	1

Обратите внимание на вид получившихся кодов. Коды одинаковой длины - это возрастающая последовательность целых чисел. Такие коды носят название канонических [5,7] и позволяют проводить быстрое кодирование и декодирование.

Кроме того, зная только длины кодов, можно достаточно быстро построить канонические коды при декодировании. Это позволяет компактно представить дополнительную информацию, которую необходимо передать декодеру, чтобы однозначно восстановить таблицу соответствия кодируемых символов и используемых для этого кодов переменной длины (таблицу перекодировки).

Например, дополнительная информация может иметь такую структуру:

Пример структуры данных, необходимый для хранения дополнительных данных

В англоязычной литературе дополнительная информация носит название “prelude”, и компактное представление такой дополнительной информации - это отдельная интересная задача, в которую я не буду сейчас углубляться. Для интересующихся оставлю ссылку на статью [8], где подробно разбирается этот вопрос.

Внимательный читатель может заметить, что построенные коды переменной длины, представленные в таблице 2, и коды Хаффмана из таблицы 1 не совпадают ни по длинам кодов, ни по их битовым представлениям (см. таблицу 3).

Таблица 3. Сравнение результатов построения кодов с минимальной избыточностью.

Входной символ	Коды Хаффмана		Канонические коды
	Длина битового кода	Битовый код	Длина битового кода	Битовый код
“H”	6	111010	6	000000
“I”	7	1110111	6	000001
“J”	7	1110110	5	00001
“E”	5	11100	5	00010
“F”	5	11011	5	00011
“G”	5	11010	5	00100
“D”	4	1100	5	00101
“C”	4	1111	4	0011
“B”	2	10	2	01
“A”	1	0	1	1

Применение алгоритма Хаффмана всегда будет создавать код с минимальной избыточностью, но не каждый возможный код с минимальной избыточностью может быть получен с помощью применения алгоритма Хаффмана. Поэтому заголовок этой заметки, строго говоря, некорректен.

Для приведённых в таблице 3 канонических кодов и кодов Хаффмана легко проверить, что неравенство Макмиллана-Крафта выполняется ( $K\leq1$ ), а средняя длина кода $l_{avg}$ одинакова и равна .

Кодирование/декодирование данных с помощью кодов переменной длины

Теперь остановимся на вопросе кодирования (сжатия) данных с использованием построенных канонических кодов.

Для этого вернёмся к нашему примеру. Пусть длины битовых кодов для каждого символа хранятся в массиве CodeLen[]. Запишем битовое представление каждого из кодов в массив CodeWord[]. Каждый элемент массива CodeWord[] - беззнаковое целое число, где биты кода выровнены по правому краю (Таблица 4).

Таблица 4. Представление кодов переменной длины для проведения кодирования.

Входной символ	CodeLen[]	Битовый код	CodeWord[]
“H”	6	000000	0
“I”	6	000001	1
“J”	5	00001	1
“E”	5	00010	2
“F”	5	00011	3
“G”	5	00100	4
“D”	5	00101	5
“C”	4	0011	3
“B”	2	01	1
“A”	1	1	1

Тогда процедура кодирования данных D длиной с помощью построенных кодов переменной длины будет иметь следующий вид:

    1   for i ← 0 to n-1
    2       do ⇨ берём очередной символ из массива входных данных D
    3          s ← D[i]
    4          l ← CodeLen[s]
    5          c ← CodeWord[s]
    6          PutBits(c, l)

В приведённой выше процедуре кодирования используется функция , которая записывает в выходной поток данных младших битов целого беззнакового числа .

Для проведения декодирования преобразуем таблицу кодов следующим образом. Во-первых, сформируем массив L_code[], где каждый элемент - беззнаковое -битное целое число, которое сформировано путём выравнивания битового кода по левому -битному краю. Здесь - максимальная длина кода.

Для нашего примера массив L_code[] представлен в таблице 5.

Таблица 5. Представление кодов переменной длины при декодировании.

Входной символ	CodeLen[]	Битовый код	L_code[]
“H”	6	000000	0
“I”	6	000001	1
“J”	5	00001	2
“E”	5	00010	4
“F”	5	00011	6
“G”	5	00100	8
“D”	5	00101	10
“C”	4	0011	12
“B”	2	01	16
“A”	1	1	32

Далее, из массива L_code[] выберем первые по порядку следования элементы, соответствующие различным длинам кодов и сформируем массив FirstCode[] (Таблица 6). В случае, если коды с некоторыми длинами отсутствуют (в нашем примере, коды с длиной, равной 3), то для них берётся следующее значение.

Таблица 6. Вспомогательный массив для проведения декодирования.

Длина битового кода	FirstCode[]
6	0
5	2
4	12
3	16
2	16
1	32
0	64

Значение FirstCode[0] необходимо нам для корректной работы алгоритма поиска длины кода при декодировании очередного закодированного символа. К этому алгоритму мы вернёмся чуть позже, а здесь лишь приведём формулу для вычисления FirstCode[0]:

FirstCode[0] = FirstCode[ $l_{min}$ ] + (1 << ( $L-l_{min}$ )),

где $l_{min}$ - минимальная длина кода, “<<” - операция битового сдвига влево.

Затем, сформируем структуру данных DecTable[][], которая для нашего примера будет иметь следующий вид:

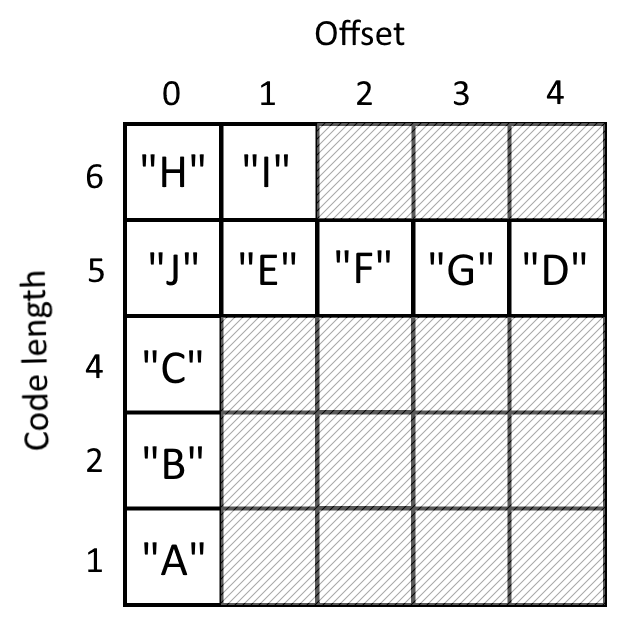
Пример структуры данных, необходимый для декодирования

Здесь offset - порядковые индексы символов, имеющих одинаковую длину кода.

Процедура декодирования будет иметь следующий вид:

    1   for i ← 0 to n-1
    2       do ⇨ получаем из потока закодированных данных L бит
    3          Buffer ← ShowBits(L)
    4          ⇨ определяем длину кода для очередного символа s
    5          for l ← L to 1
    6              do if FirstCode[l] ≤ Buffer < FirstCode[l-1] 
    7                     then goto line 8
    8          ⇨ на основании найденной длины кода декодируем символ s
    9          offset ← (Buffer - FirstCode[l]) >> (L - l)
    10          s ← DecTable[l][offset]
    11         ⇨ удаляем l битов из потока закодированных данных
    12         RemoveBits(l)

Приведённую выше процедуру декодирования можно ускорить, если линейный поиск длины кода (строки 5 - 7) заменить алгоритмом бинарного поиска:

    1   for i ← 0 to n-1
    2       do ⇨ получаем из потока закодированных данных L бит
    3          Buffer ← ShowBits(L)
    4          ⇨ определяем длину кода для очередного символа s
    5          left ← 0, right ← L + 1
    6          while (right - left) > 1
    7          do
    8              middle = (right + left) / 2
    9              if FirstCode[middle] ≤ Buffer
    10             then
    11                 right ← middle
    12             else
    13                 left ← middle
    14          ⇨ на основании найденной длины кода декодируем символ s
    15          offset ← (Buffer - FirstCode[right]) >> (L - right)
    16          s ← DecTable[right][offset]
    17         ⇨ удаляем right битов из потока закодированных данных
    18         RemoveBits(right)

Если мы вернёмся к описанию процедуры кодирования, то можно заметить, что суммарное число битов для закодированных данных может быть некратно 8. Это значит, что при записи закодированных данных в память или файл на диске нам необходимо дополнить закодированные данные таким числом битов, чтобы получить целое число байтов (например, добавить нулевые биты, если это необходимо).

Однако эти дополнительные биты должны быть проигнорированы при декодировании. В описанной выше процедуре декодирования предполагается, что мы передаём исходный размер данных (длину незакодированных данных ) вместе с закодированной информацией.

Следует заметить, что это - не единственный способ, необходимый для правильного декодирования данных. Другим вариантом является включение в алфавит входных символов еще одного специального символа (обозначим его - “EndOfData”), частота появления которого полагается равной 1. Тогда для символа будет построен префиксный код. Мы помещаем в конец кодируемых данных, а при декодировании появление кода для остановит процедуру декодирования. У такого способа остановки декодирования есть один недостаток, о котором мы поговорим позднее.

Вопросы практической реализации

Теперь предлагаю перейти в практическую плоскость и рассмотреть проблемы реализации описанных до этого алгоритмов для реальных вычислительных систем.

При описании процедуры построения битовых кодов по найденным длинам, мы предполагали, что целые числа $B[i], 0 \leq i < n$ , которые служат для хранения битовых представлений кодов, имеют достаточный для этого размер в битах (битовую разрядность).

Так как мы изначально договорились, что входные символы — это байты, то входной алфавит будет состоять из 256 символов. Символы такого алфавита могут иметь вероятности $2^{-1}, 2^{-1}, ..., 2^{-255}, 2^{-255}$ , что при построении префиксных кодов приведёт к появлению двух кодов с длиной 255 битов каждый. На практике для таких распределений применяют другие методы кодирования, например арифметическое кодирование [1].

Тем не менее, в худшем случае нам необходимо предусмотреть возможность хранения битовых кодов большой длины.

Далее, разрядность целых чисел задаётся разрядностью вычислительной системы (для педантов - разрядностью машинного слова вычислительной системы). Для ноутбука, на котором я писал этот текст, разрядность равна 64 битам. И для работы с битовыми кодами, длина которых превышает 64 бита, необходима реализация специальных алгоритмов, которые будут осуществлять базовые операции для таких кодов, что в большинстве случаев приводит к катастрофическому замедлению работы алгоритмов кодирования.

Чтобы решить эту проблему, при реализации алгоритма кодирования мы можем до некоторой степени пожертвовать степенью сжатия в обмен на обеспечение высокой скорости кодирования/декодирования. Рассмотрим два основных подхода к решению этой проблемы.

Применение алгоритма ограничения максимальной длины кода.

Входными данными для этого алгоритма является массив , содержащий длины кодов для каждого символа входного алфавита из символов.

    1    ⇨ подсчитываем число символов с одинаковыми длинами кодов
    2   for i ← 0 to n-1
    3       do m[i] ← 0
    4   for i ← 0 to n-1
    5       do m[A[i]] ← m[A[i]] + 1
    6    ⇨ пересчитаем количество кодов с длинами, меньшими требуемой L_restrict
    7   for i ← L downto L_restrict+1
    8       do while m[i] > 0
    9          do
    10            j ← i - 1
    11            do
    12               j ← j - 1
    13            while m[j] ≤ 0
    14            m[i] ← m[i] - 2
    15            m[i-1] ← m[i-1] + 1
    16            m[j+1] ← m[j+1] + 2
    17            m[j] ← m[j] - 1
    18    ⇨ переназначим длины кодов символам входного алфавита
    19   n ← 0
    20   for i ← L_restrict downto 1
    21   do
    22       k ← m[i]
    23       while k > 0
    24       do
    25          A[n] ← i
    26          n ← n + 1
    27          k ← k - 1

Приведённый выше алгоритм ограничения максимальной длины кода состоит из 3 этапов [9]. На первом этапе (строки 1 - 5) производится подсчёт числа кодов для каждой из длин , где - максимальная длина кода. Результат такого подсчёта записывается в массив (точно также как и в начале процедуры формирования битовых кодов по их длинам).

Второй этап (строки 6 - 17) заключается в пересчёте количества кодов с длинами, меньшими требуемой величины $L\_restrict$ , так, чтобы длины кодов для всех символов входного алфавита были меньше или равны $L\_restrict$ .

Так как два символа входного алфавита (два листа двоичного дерева) формируют одну вершину-родителя, то на каждой итерации внутреннего цикла (строки 8 - 17) мы берём пару символов с длиной кода . Для этих двух символов вершина-родитель будет иметь длину кода . Затем мы ищем символ с длиной кода, меньшей чем , и заменяем его выбранной вершиной-родителем. При этом заменяемый символ помещается на место вершины-родителя. Звучит очень запутанно, поэтому предлагаю рассмотреть работу этого этапа для нашего примера, полагая $L\_restrict = 4$ .

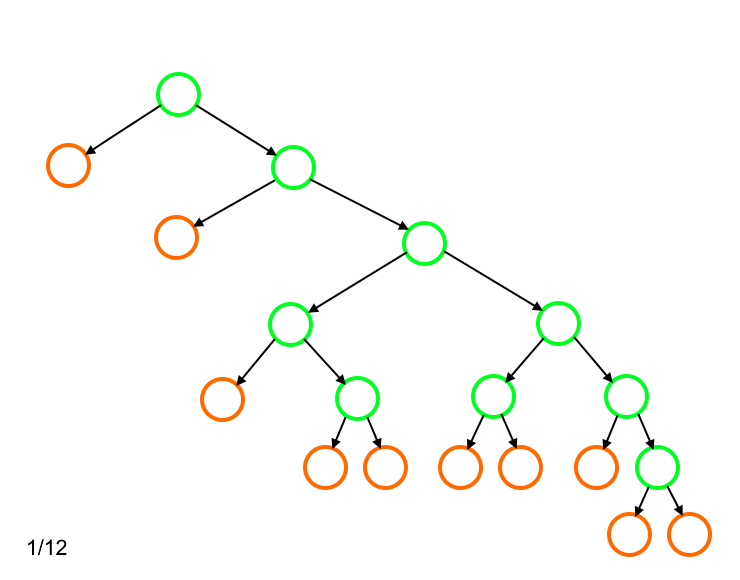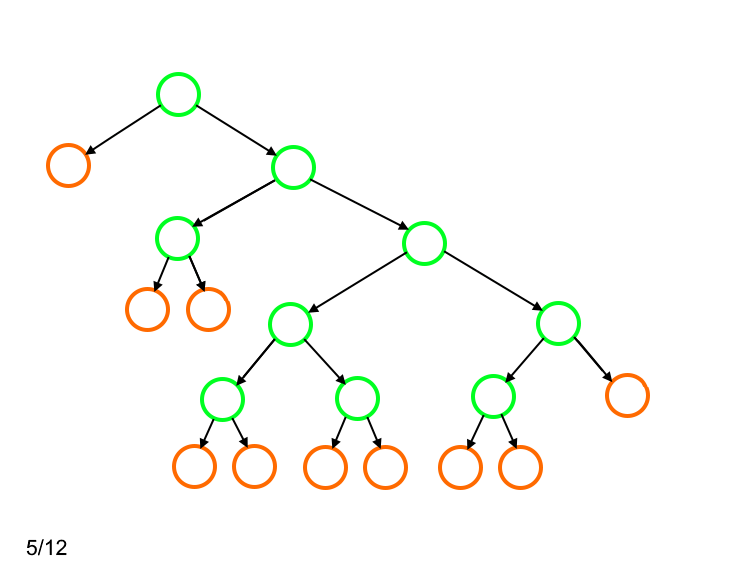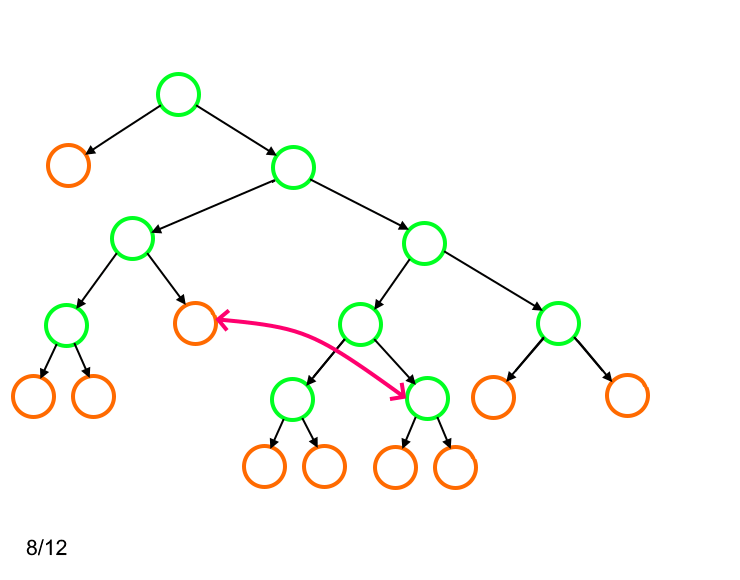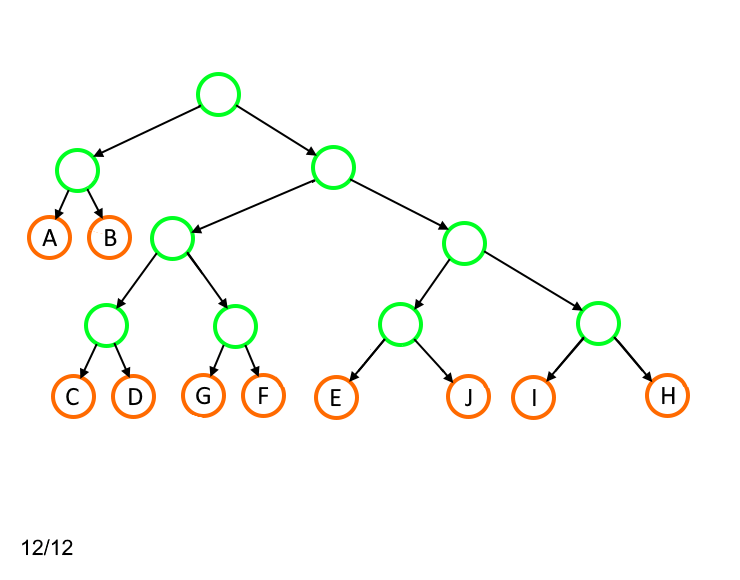
Пример работы алгоритма ограничения максимальной длины кода

Алгоритм оперирует количеством символов, для которых длина кода одинакова. Поэтому нам оказывается неважной привязка каждого листа к определённому символу входного алфавита. Такая перепривязка производится на третьем этапе (строки 18 - 27).

Корректная работа приведённого алгоритма гарантируется при следующем условии:

$L\_restrict >= \lceil log_2(size(A)) \rceil,$

где - размер входного алфавита.

По сути указанное выше ограничение - это минимально возможная высота двоичного дерева с количеством листов, равным количеству символов входного алфавита. Для нашего примера такое дерево будет иметь следующий вид:

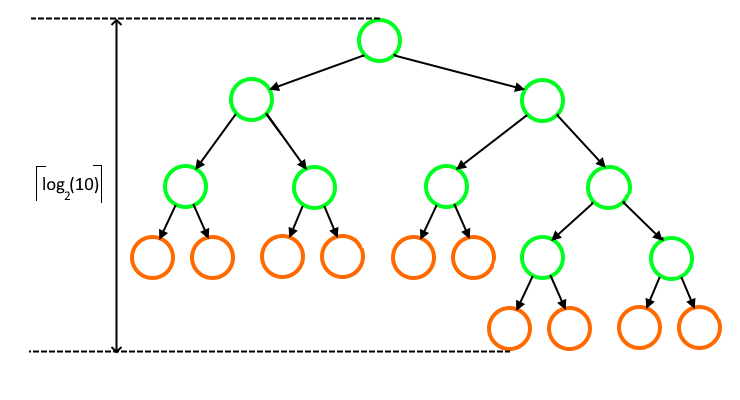
Двоичное дерево мимниальной длины для алфавита из 10 символов

Для такого дерева применить описанный алгоритм невозможно, так как на определённом шаге будут отсутствовать листья, которые можно было бы заменить вершиной-родителем для двух листов, имеющих длину кода 4.

Применение escape-кодирования.

Так как редко встречающимся символам входного алфавита назначаются более длинные коды по сравнению с часто встречающимися символами, то одной из возможностей ограничить максимальную длину получающихся кодов является кодирование группы редко встречающихся символов парой .

Здесь - префиксный код псевдосимвола, имеющего частоту появления, равную сумме частот появления символов из группы редко встречающихся символов, - код фиксированной длины, позволяющий однозначно декодировать символ из этой группы. Такая схема кодирования в литературе носит название escape-кодирования (кодирования с использованием escape-псевдосимвола).

Хотелось бы заметить, что вариант escape-кодирования применяется в случае, если размер входного алфавита оказывается достаточно большим, и построение кодов переменной длины для каждого символа будет гарантированно приводить к появлению кодов с большими длинами.

Например, в стандарте JPEG требуется кодировать целые числа из диапазона , и каждый символ кодируется парой , где - префиксный код, кодирующий информацию о длине цепочки нулевых символов, предшествующих очередному ненулевому кодируемому символу, а также о количестве битов, необходимых для однозначного декодирования этого ненулевого символа. имеет длину, равную количеству битов, которое закодировано в . Более подробное описание такой схемы кодирования можно найти в [10]. Английский язык там достаточно простой, а автор излагает суть алгоритмов, используемых в стандарте JPEG, простыми словами.

Вернёмся обратно к нашей проблеме ограничения максимальной длины кода. Проведём замену символов с длинами кодов, большими требуемой величины $L\_restrict$ , парой символов . - код переменной длины длиной $L\_restrict$ , - код фиксированной длины. Так как мы договорились что входные символы - это байты, то размер кода может быть равен 8 битам.

Рассмотрим такую процедуру ограничения максимальной длины кода для нашего примера. Пусть, как и в предыдущем случае, $L\_restrict = 4$ . Тогда таблица кодирования будет выглядеть следующим образом:

Таблица 7. Схема кодирования с использованием escape-символа.

Входной символ	CodeLen[]	CodeWord[]	FixedCodeWord[]
“H”	4	0011	111
“I”	4	0011	110
“J”	4	0011	101
“E”	4	0011	100
“F”	4	0011	011
“G”	4	0011	010
“D”	4	0011	001
“C”	4	0011	000
“B”	2	01	-
“A”	1	1	-

Исходя из числа символов, которые будут кодироваться с помощью escape-символа, длина кода будет равна 3 битам, что позволяет однозначно декодировать символы входного алфавита.

Процедура кодирования данных D длиной будет иметь следующий вид:

    1   for i ← 0 to n-1
    2       do ⇨ берём очередной символ из массива входных данных D
    3          s ← D[i]
    4          if s ∈ группе символов, кодируемых с помощью escape-символа
    5          then ⇨ помещаем в выходной битовый поток код, соответствующий escape-символу
    6               l ← CodeLen[s]
    7               c ← CodeWord[s]
    8               PutBits(c, l)
    9               ⇨ помещаем в выходной битовый поток код фиксированной длины
    10              l ← FixedCodeLen
    11              c ← FixedCodeWord[s]
    12              PutBits(c, l)
    13         else ⇨ кодируем символ напрямую с помощью кода переменной длины
    14              l ← CodeLen[s]
    15              c ← CodeWord[s]
    16              PutBits(c, l)

Здесь FixedCodeLen - наперёд заданная длина кода фиксированной длины.

Процедура декодирования очевидно вытекает из процедуры кодирования. Как только из входного кодированного потока появляется код, соответствующий escape-символу, то производится считывание FixedCodeLen битов, которые помогают однозначно декодировать символ входного алфавита.

Приведённая схема кодирования снижает степень сжатия данных в обмен на ограничение максимальной длины кода с целью ускорения кодирования/декодирования. Чтобы поднять степень сжатия и при этом не потерять в скорости кодирования/декодирования, можно использовать не один, а несколько escape-символов, а также осуществить предобработку входных данных перед их кодированием. Но здесь я бы не хотел углубляться в эту тему, так как этo требует, на мой взгляд, отдельной заметки, а то и целой серии статей.

В заключение, необходимо заметить, что ограничение максимальной длины кода может помочь сделать декодирование достаточно быстрым.

Быстрое декодирование

Напомним, что - максимальная длина кода. Тогда при декодировании мы можем построить одномерную таблицу соответствия, которая может ускорить процедуру декодирования.

Для нашего примера такая одномерная таблица будет выглядеть так:

Таблица 8. Пример одномерной таблицы соответствия для быстрого декодирования.

Битовый L-битный код	Фактическая длина кода	Входной символ
000000	6	“H”
000001	6	“I”
000010	5	“J”
000011	5	“J”
000100	5	“E”
000101	5	“E”
000110	5	“F”
000111	5	“F”
001000	5	“G”
001001	5	“G”
001010	5	“D”
001011	5	“D”
001100	4	“C”
001101	4	“C”
001110	4	“C”
001111	4	“C”
010000	2	“B”
010001	2	“B”
…	…	…
011110	2	“B”
011111	2	“B”
100000	1	“A”
…	…	…
111111	1	“A”

Битовый -битный код задаёт адрес в одномерной таблице соответствия, по которому в процессе декодирования определяется фактическая длина кода и символ.

В этом случае процедура декодирования имеет следующий вид:

    1   for i ← 0 to n-1
    2       do ⇨ получаем из потока закодированных данных L бит
    3          Buffer ← ShowBits(L)
    4          ⇨ определяем длину кода и декодируем очередной символ
    5          s ← FastDecSymbolTable[Buffer]
    6          l ← FastDecLenTable[Buffer]
    7          ⇨ удаляем l битов из потока закодированных данных
    8          RemoveBits(l)

Здесь - это длина незакодированных данных, FastDecSymbolTable и FastDecLenTable— одномерные массивы, содержащие декодированный символ и соответствующую ему длину кода.

Таким образом, вычислительная сложность декодирования уменьшится с (для декодирования, использующего бинарный поиск) до .

Размер массивов FastDecSymbolTable и FastDecLenTable равен . Если достаточно большое, то указанные массивы будут огромного размера, и в худшем случае не поместятся в оперативной памяти вычислительной системы. А даже если и поместятся, то фактическая скорость декодирования будет невелика из-за постоянных обращений к оперативной памяти. Поэтому приведённая процедура быстрого декодирования имеет смысл, если массивы FastDecSymbolTable и FastDecLenTable будут помещаться в кеш (“cache”) вычислительной системы.

В заключение хотелось бы отметить, что за рамками этой заметки остались такие важные вопросы, как: применимость кодирования данных с использованием кодов переменной длины, моделирование вероятностей при кодировании данных, а также общие вопросы теории энтропийного кодирования. Я сознательно старался не касаться этих тем, а сосредоточиться на алгоритме построения кодов переменной длины и его практической реализации.

Хочу поблагодарить Ивана Соломатина за помощь и ценные советы в процессе подготовки этой публикации.

Алексей Фартуков

руководитель лаборатории Samsung

Литература

Д. Ватолин, А. Ратушняк, М. Смирнов, В. Юкин. Методы сжатия данных. Устройство архиваторов, сжатие изображений и видео. Диалог-МИФИ - 2003.
Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ, 3-е издание. Вильямс - 2013.
Алгоритм сжатия Хаффмана. Перевод MaxRokatansky. Блог компании OTUS. https://habr.com/ru/company/otus/blog/497566/ - 2020.
Яблонский С. В. Введение в дискретную математику. М.: Наука - 1986.
A. Moffat, T.C. Bell and I. H. Witten. Lossless Compression for Text and Images. International Journal of High Speed Electronics and Systems. Vol. 08, No. 01, pp. 179-231 (https://doi.org/10.1142/S0129156497000068) - 1997.
A. Moffat and J. Katajainen. In-Place Calculation of Minimum-Redundancy Codes. WADS ’95: Proceedings of the 4th International Workshop on Algorithms and Data Structures, pp. 393–402 - 1995.
A. Moffat. Huffman Coding. ACM Computing Surveys. Vol. 52 Issue 4, pp. 1–35 ( https://doi.org/10.1145/3342555) - 2020.
A. Turpin and A. Moffat. Housekeeping for prefix coding. IEEE Transactions on Communications, vol. 48, no. 4, pp. 622-628, April 2000, doi: 10.1109/26.843129.
T.81 : Information technology - Digital compression and coding of continuous-tone still images - Requirements and guidelines (09/92) https://www.w3.org/Graphics/JPEG/itu-t81.pdf
Cristi Cuturicu. A note about the JPEG decoding algorithm. http://www.opennet.ru/docs/formats/jpeg.txt - 1999.

Теги:

Хабы: