
Много людей, в первый раз сталкивающихся в работе с датчиками, склонны считать, что получаемые показания — это точные значения. Некоторые вспоминают, что в показаниях всегда есть погрешности и ошибки. Чтобы ошибки в измерениях не приводили к ошибкам в функционировании системы в целом, данные датчиков необходимо обрабатывать. На ум сразу приходит словосочетание “фильтр Калмана”. Но слава этого “страшного” алгоритма, малопонятные формулы и разнообразие используемых обозначений отпугивают разработчиков. Постараемся разобраться с ним на практическом примере.
Об алгоритме
Что же нам потребуется для работы фильтра Калмана?
- Нам потребуется модель системы.
- Модель должна быть линейной (об этом чуть позже).
- Нужно будет выбрать переменные, которые будут описывать состояние системы (“вектор состояния”).
- Мы будем производить измерения и вычисления в дискретные моменты времени (например, 10 раз в секунду). Нам потребуется модель наблюдения.
- Для работы фильтра достаточно данных измерений в текущий момент времени и результатов вычислений с предыдущего момента времени.
Алгоритм работает итеративно. На каждом шаге алгоритм берёт данные датчиков (с шумом и другими проблемами), вектор состояния с предыдущего шага и по этим данным оценивает состояние системы на текущем шаге. Кроме того, он еще отслеживает насколько мы можем быть уверены, что наш текущий вектор состояний соответствует истинному положению дел (разброс значений для каждой переменной в векторе).
Обычно используются следующие обозначения:
Содержимое вектора состояния зависит от фантазии разработчика и решаемой задачи. Например, мы можем отслеживать координаты объекта, а также его скорость и ускорение. В этом случае получается вектор из трёх переменных: {позиция, скорость, ускорение} (для одномерного случая; для 3D мира будет по одному такому набору для каждой оси, то есть, 9 значений в векторе)
По сути, речь идёт о совместном распределении случайных величин
В фильтре Калмана мы предполагаем, что все погрешности и ошибки (как во входных данных, так и в оценке вектора состояния) имеют нормальное распределение. А для многомерного нормального распределения его полностью определяют два параметра: математическое ожидание вектора и его ковариационная матрица.
Математическая модель системы / процесса
Мы имеем дело с динамической системой, т.е. состояние системы меняется со временем. Имея модель системы, фильтр Калмана может предугадывать, каким будет состояние системы в следующий момент времени. Именно это позволяет фильтру так эффективно устранять шум и оценивать параметры, которые не наблюдаются (не измеряются) напрямую.
Фильтр Калмана накладывает ограничения на используемые модели: это должны быть дискретные модели в пространстве состояний. А ещё они должны быть линейными.
Дискретные и линейные?
Дискретность означает для нас то, что модель работает “шагами”. На каждом шаге мы вычисляем новое состояние системы по вектору состояния с предыдущего шага. Обычно, модели такого рода задаются системой разностных уравнений.
По поводу линейности: каждое уравнение системы является линейным уравнением, задающим новое значение переменной состояния. Т.е. никаких косинусов, синусов, возведений в степень и даже сложений с константой.
По поводу линейности: каждое уравнение системы является линейным уравнением, задающим новое значение переменной состояния. Т.е. никаких косинусов, синусов, возведений в степень и даже сложений с константой.
Такую модель удобно представлять в виде разностного матричного уравнения:
Давайте разберём это уравнение подробно. В первую очередь, нас интересует первое слагаемое (
Например, для равноускоренного движения матрица будет выглядеть так:
Первая строка матрицы — хорошо знакомое уравнение
А что же с остальными слагаемыми?
В некоторых случаях, мы напрямую управляем процессом (например, управляем квадракоптером с помощью пульта Д/У) и нам достоверно известны задаваемые параметры (заданная на пульте скорость полёта). Второе слагаемое — это модель управления. Матрица  называется матрицей управления, а вектор
называется матрицей управления, а вектор  — вектор управляющих воздействий. В случаях когда мы только наблюдаем за процессом, это слагаемое отсутствует.
— вектор управляющих воздействий. В случаях когда мы только наблюдаем за процессом, это слагаемое отсутствует.
Последнее слагаемое — — это вектор ошибки модели. Модель равноускоренного движения абсолютно точно описывает положение объекта. Однако в реальном мире есть множество случайных факторов — дороги неровные, дует ветер, и т.п. Иногда, процесс сложен и приходится использовать упрощённую модель, которая не учитывает все аспекты. Именно так возникает ошибка модели.
— это вектор ошибки модели. Модель равноускоренного движения абсолютно точно описывает положение объекта. Однако в реальном мире есть множество случайных факторов — дороги неровные, дует ветер, и т.п. Иногда, процесс сложен и приходится использовать упрощённую модель, которая не учитывает все аспекты. Именно так возникает ошибка модели.
То, что мы записываем это слагаемое, не означает, что мы знаем ошибку на каждом шаге или описываем её аналитически. Однако фильтр Калмана делает важное предположение — ошибка имеет нормальное распределение с нулевым математическим ожиданием и ковариационной матрицей . Эта матрица очень важна для стабильной работы фильтра и мы её рассмотрим позже.
. Эта матрица очень важна для стабильной работы фильтра и мы её рассмотрим позже.
Последнее слагаемое —
То, что мы записываем это слагаемое, не означает, что мы знаем ошибку на каждом шаге или описываем её аналитически. Однако фильтр Калмана делает важное предположение — ошибка имеет нормальное распределение с нулевым математическим ожиданием и ковариационной матрицей
Модель наблюдения
Не всегда получается так, что мы измеряем интересующие нас параметры напрямую (например, мы измеряем скорость вращения колеса, хотя нас интересует скорость автомобиля). Модель наблюдения описывает связь между переменными состояния и измеряемыми величинами:
Первое слагаемое
Второе слагаемое
Вернёмся к нашему примеру. Пусть у нас на роботе установлен один единственный датчик — GPS приёмник (“измеряет” положение). В этом случае матрица
Строки матрицы соответствуют переменным в векторе состояния, столбцы — элементам вектора измерений. В первой строке матрицы находится значение “1” так как единица измерения положения в векторе состояния совпадает с единицей измерения значения в векторе измерений. Остальные строки содержат “0” потому что переменные состояния соответствующие этим строкам не измеряются датчиком.
Что будет, если датчик и модель используют разные единицы измерения? А если датчиков несколько?
Например, модель использует метры, а датчик — количество оборотов колеса. В этом случае матрица будет выглядеть так:
Количество датчиков ничем (кроме здравого смысла) не ограничено.
Например, добавим спидометр:
Второй столбец матрицы соответствует нашему новому датчику.
Несколько датчиков могут измерять один и тот же параметр. Добавим ещё один датчик скорости:
Количество датчиков ничем (кроме здравого смысла) не ограничено.
Например, добавим спидометр:
Второй столбец матрицы соответствует нашему новому датчику.
Несколько датчиков могут измерять один и тот же параметр. Добавим ещё один датчик скорости:
Ковариационные матрицы и где они обитают
Для настройки фильтра нам потребуется заполнить несколько ковариационных матриц:
Ковариационные матрицы?
Для нормально распределенной случайной величины её математическое ожидание и дисперсия полностью определяют её распределение. Дисперсия — это мера разброса случайной величины. Чем больше дисперсия — тем сильнее может отклоняться случайная величина от её математического ожидания. Ковариационная матрица — это многомерный аналог дисперсии, для случая, когда у нас не одна случайная величина, а случайный вектор.
В одной статье сложно уместить всю теорию вероятностей, поэтому ограничимся сугубо практическими свойствами ковариационных матриц. Это симметричные квадратные матрицы, на главной диагонали которой располагаются дисперсии элементов вектора. Остальные элементы матрицы — ковариации между компонентами вектора. Ковариация показывает, насколько переменные зависят друг от друга.
Проиллюстрируем влияние мат. ожидания, дисперсии и ковариации.
Начнём с одномерного случая. Функция плотности вероятности нормального распределения — знаменитая колоколообразная кривая. Горизонтальная ось — значение случайной величины, а вертикальная ось — сравнительная вероятность того что случайная величина примет это значение:

Чем меньше дисперсия — тем меньше ширина колокола.
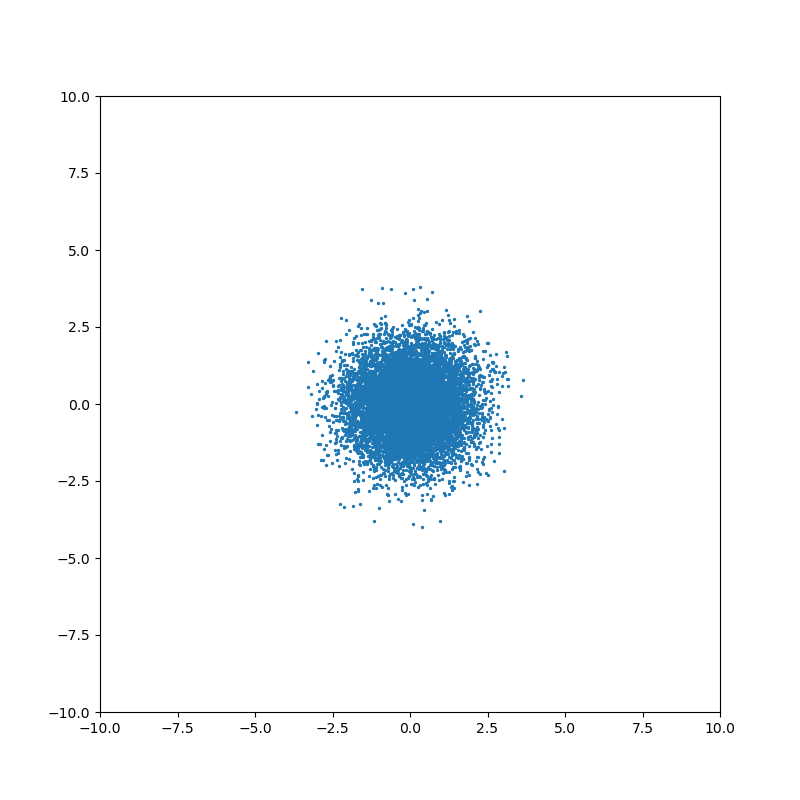
Понятие ковариации возникает для совместного распределения нескольких случайных величин. Когда случайные величины независимы, то ковариация равна нулю:

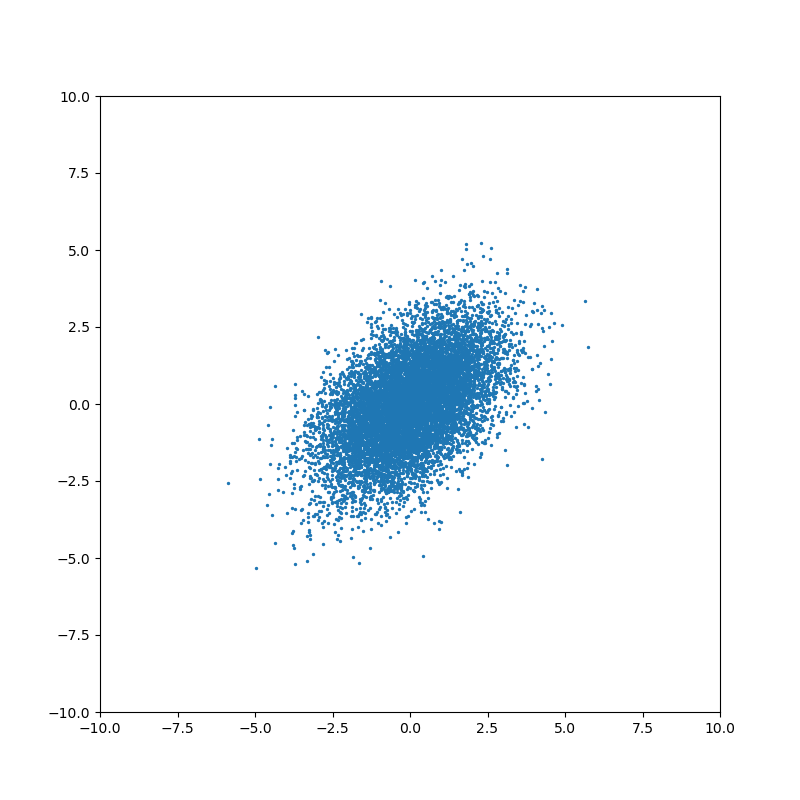
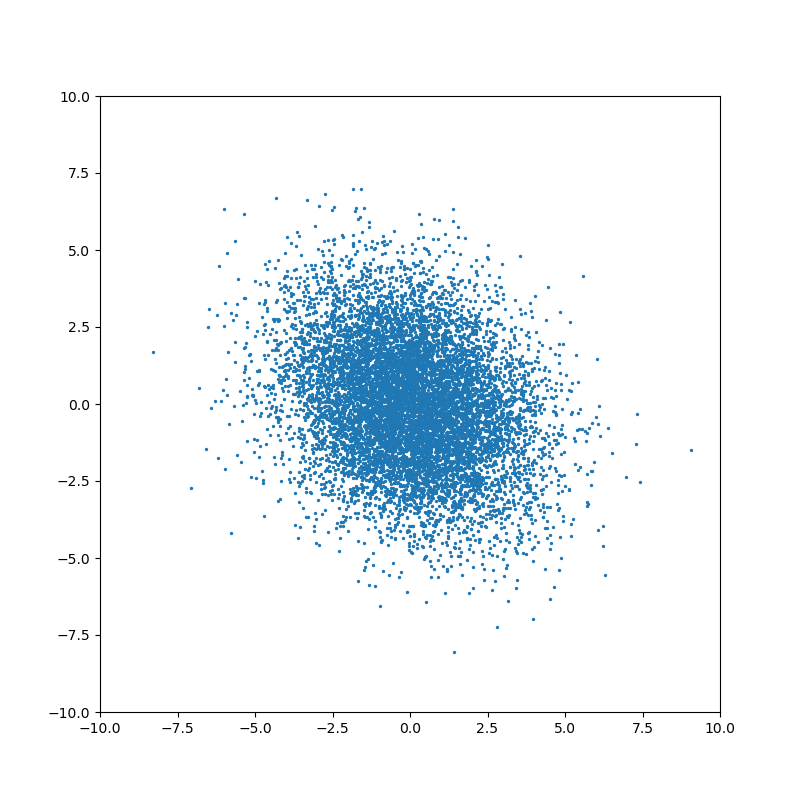
Ненулевое значение ковариации означает, что существует связь между значениями случайных величин:


В одной статье сложно уместить всю теорию вероятностей, поэтому ограничимся сугубо практическими свойствами ковариационных матриц. Это симметричные квадратные матрицы, на главной диагонали которой располагаются дисперсии элементов вектора. Остальные элементы матрицы — ковариации между компонентами вектора. Ковариация показывает, насколько переменные зависят друг от друга.
Проиллюстрируем влияние мат. ожидания, дисперсии и ковариации.
Начнём с одномерного случая. Функция плотности вероятности нормального распределения — знаменитая колоколообразная кривая. Горизонтальная ось — значение случайной величины, а вертикальная ось — сравнительная вероятность того что случайная величина примет это значение:

Чем меньше дисперсия — тем меньше ширина колокола.
Понятие ковариации возникает для совместного распределения нескольких случайных величин. Когда случайные величины независимы, то ковариация равна нулю:

Ненулевое значение ковариации означает, что существует связь между значениями случайных величин:


На каждом шаге фильтр Калмана строит предположение о состоянии системы, исходя из предыдущей оценки состояния и данных измерений. Если неопределенности вектора состояния выше, чем ошибка измерения, то фильтр будет выбирать значения ближе к данным измерений. Если ошибка измерения больше оценки неопределенности состояния, то фильтр будет больше “доверять” данным моделирования. Именно поэтому важно правильно подобрать значения ковариационных матриц — основного инструмента настройки фильтра.
Рассмотрим каждую матрицу подробнее:
Квадратная матрица, порядок матрицы равен размеру вектора состояния
Как уже было сказано выше, эта матрица определяет “уверенность” фильтра в оценке переменных состояния. Алгоритм самостоятельно обновляет эту матрицу в процессе работы. Однако нам нужно установить начальное состояние, вместе с исходным предположением о векторе состояния.
Во многих случаях нам неизвестны значения ковариации между переменными для изначального состояния (элементы матрицы, расположенные вне главной диагонали). Поэтому можно проигнорировать их, установив равными 0. Фильтр самостоятельно обновит значения в процессе работы. Если же значения ковариации известны, то, конечно же, стоит использовать их.
Дисперсию же проигнорировать не выйдет. Необходимо установить значения дисперсии в зависимости от нашей уверенности в исходном векторе состояния. Для этого можно воспользоваться правилом трёх сигм: значение случайной величины попадает в диапазон
Пример
Допустим, нам нужно установить дисперсию для переменной состояния — скорости робота. Мы знаем что максимальная скорость передвижения робота — 10 м/с. Но начальное значение скорости нам неизвестно. Поэтому, мы выберем изначальное значение переменной — 0 м/с, а среднеквадратичное отклонение  ;
;  Соответственно, дисперсия
Соответственно, дисперсия  .
.
Квадратная матрица, порядок матрицы равен размеру вектора наблюдения (количеству измеряемых параметров).
Во многих случаях можно считать, что измерения не коррелируют друг с другом. В этом случае матрица
Квадратная матрица, порядок матрицы равен размеру вектора состояния.
С этой матрицей обычно возникает наибольшее количество вопросов. Что означает ошибка модели? Каков смысл этой матрицы и за что она отвечает? Как заполнять эту матрицу? Рассмотрим всё по порядку.
Каждый раз, когда фильтр предсказывает состояние системы, используя модель процесса, он увеличивает неуверенность в оценке вектора состояния. Для одномерного случая формула выглядит приблизительно следующим образом:
Если установить очень маленькое значение
Если же установить большое значение
Для многомерного случая формула выглядит несколько сложнее, но смысл схожий. Однако, есть важное отличие: эта матрица указывает, на какие переменные состояния будут в первую очередь влиять ошибки модели и неучтённые факторы.
Допустим, мы отслеживаем перемещение робота, используя модель равноускоренного движения, и вектор состояния содержит следующие переменные: положение x, скорость v и ускорение a. Однако, наша модель не учитывает, что на дороге встречаются неровности.
Когда робот проходит неровность, показания датчиков и предсказание модели начнут расходиться. Структура матрицы
Мы можем выдвинуть различные предположения относительно природы шума. Для нашего примера с равноускоренным движением логично было бы предположить, что неучтённые факторы (неровность дороги) в первую очередь влияют на ускорение. Этот подход применим ко многим структурам модели, где в векторе состояния присутствует переменная и несколько её производных по времени (например, положение и производные: скорость и ускорение). Матрица
Так как же заполняется матрица Q?
Обычно используют модель-приближение. Рассмотрим на примере модели равноускоренного движения:
Мы предполагаем, что ускорение постоянно на каждом шаге. Но из-за неровностей дороги ускорение, на самом деле, постоянно изменяется. Мы можем предположить, что изменение ускорения происходит под воздействием непрерывного белого шума с нулевым математическим ожиданием (т.е. усреднив все небольшие изменения ускорения за время движения робота мы получаем 0)
В этой модели матрица Q рассчитывается следующим образом
Для нашей модели равноускоренного движения матрица будет выглядеть так:
 — спектральная плотность мощности белого шума
— спектральная плотность мощности белого шума
Подставляем матрицу процесса, соответствующую нашей модели:
Мы предполагаем, что ускорение на самом деле постоянно в течение каждого шага моделирования, но дискретно и независимо меняется между шагами. Выглядит очень похоже на предыдущую модель, но небольшая разница есть
 — мощность шума
— мощность шума
 — наивысший порядок производной, используемой в модели (т.е. ускорение для вышеописанной модели)
— наивысший порядок производной, используемой в модели (т.е. ускорение для вышеописанной модели)
В этой модели матрица определяется следующим образом:
определяется следующим образом:
и подставляем в формулу. В итоге получаем:
Обе модели являются приближениями того, что происходит на самом деле в реальности. На практике, приходится экспериментировать и выяснять, какая модель подходит лучше в каждом отдельном случае. Плюсом второй модели является то, что мы оперируем дисперсией шума, с которой уже хорошо умеем работать.
Модель непрерывного белого шума
Мы предполагаем, что ускорение постоянно на каждом шаге. Но из-за неровностей дороги ускорение, на самом деле, постоянно изменяется. Мы можем предположить, что изменение ускорения происходит под воздействием непрерывного белого шума с нулевым математическим ожиданием (т.е. усреднив все небольшие изменения ускорения за время движения робота мы получаем 0)
В этой модели матрица Q рассчитывается следующим образом
Для нашей модели равноускоренного движения матрица будет выглядеть так:
Подставляем матрицу процесса, соответствующую нашей модели:
Модель “кусочного” белого шума
Мы предполагаем, что ускорение на самом деле постоянно в течение каждого шага моделирования, но дискретно и независимо меняется между шагами. Выглядит очень похоже на предыдущую модель, но небольшая разница есть
В этой модели матрица
и подставляем в формулу. В итоге получаем:
Обе модели являются приближениями того, что происходит на самом деле в реальности. На практике, приходится экспериментировать и выяснять, какая модель подходит лучше в каждом отдельном случае. Плюсом второй модели является то, что мы оперируем дисперсией шума, с которой уже хорошо умеем работать.
Простейший подход
В некоторых случаях прибегают к грубому упрощению: устанавливают все элементы матрицы
Действительно, если рассчитать
Т.е. для нашей модели равноускоренного движения можно взять матрицу
Важное замечание
Во всех примерах выше используется вектор состояния
Рассмотрим вектор состояния
Матрица
Дисперсия, соответствующая наивысшим порядкам производных
Однако, на практике нет никакого смысла перемешивать порядок переменных состояния таким образом, чтобы порядки производных шли не по очереди — это просто неудобно.
Пример кода
Нет смысла изобретать велосипед и писать свою собственную реализацию фильтра Калмана, когда существует множество готовых библиотек. Я выбрал язык python и библиотеку filterpy для примера.
Чтобы не загромождать пример, возьмем одномерный случай. Одномерный робот оборудован одномерным GPS, который определяет положение с некоторой погрешностью.
Моделирование данных датчиков
Начнём с равномерного движения:
Simulator.py
import numpy as np
import numpy.random
# Моделирование данных датчика
def simulateSensor(samplesCount, noiseSigma, dt):
# Шум с нормальным распределением. мат. ожидание = 0, среднеквадратичное отклонение = noiseSigma
noise = numpy.random.normal(loc = 0.0, scale = noiseSigma, size = samplesCount)
trajectory = np.zeros((3, samplesCount))
position = 0
velocity = 1.0
acceleration = 0.0
for i in range(1, samplesCount):
position = position + velocity * dt + (acceleration * dt ** 2) / 2.0
velocity = velocity + acceleration * dt
acceleration = acceleration
trajectory[0][i] = position
trajectory[1][i] = velocity
trajectory[2][i] = acceleration
measurement = trajectory[0] + noise
return trajectory, measurement # Истинное значение и данные "датчика" с шумом
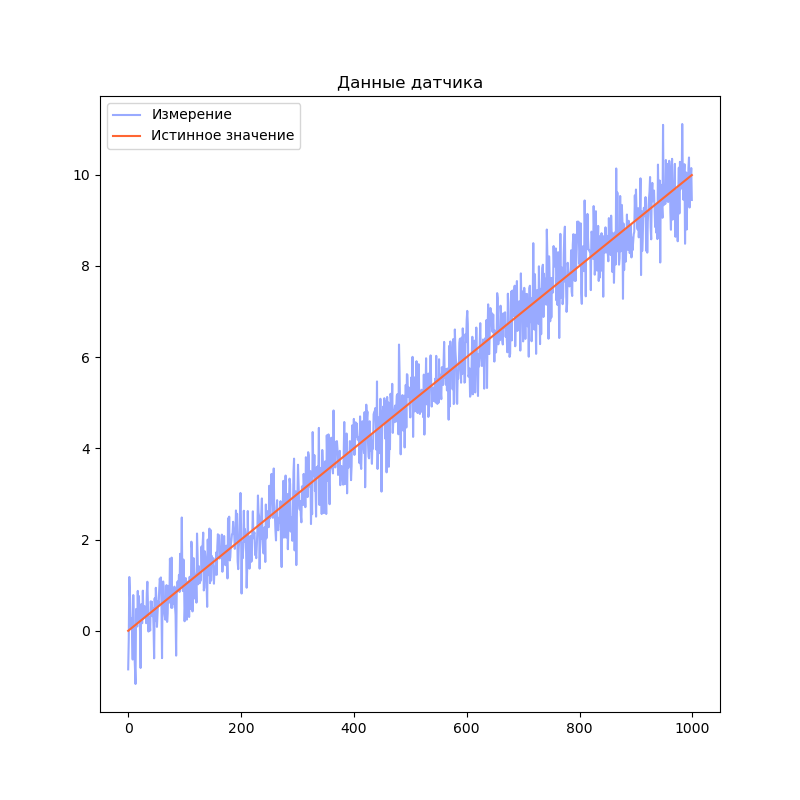
Визуализируем результаты моделирования:
Код
import matplotlib.pyplot as plt
dt = 0.01
measurementSigma = 0.5
trajectory, measurement = simulateSensor(1000, measurementSigma, dt)
plt.title("Данные датчика")
plt.plot(measurement, label="Измерение", color="#99AAFF")
plt.plot(trajectory[0], label="Истинное значение", color="#FF6633")
plt.legend()
plt.show()

Реализация фильтра
Для начала выберем модель системы. Я решил взять 3 переменных состояния: положение, скорость и ускорение. В качестве модели процесса возьмем модель равноускоренного движения:
Код
import filterpy.kalman
import filterpy.common
import matplotlib.pyplot as plt
import numpy as np
import numpy.random
from Simulator import simulateSensor # моделирование датчиков
dt = 0.01 # Шаг времени
measurementSigma = 0.5 # Среднеквадратичное отклонение датчика
processNoise = 1e-4 # Погрешность модели
# Моделирование данных датчиков
trajectory, measurement = simulateSensor(1000, measurementSigma, dt)
# Создаём объект KalmanFilter
filter = filterpy.kalman.KalmanFilter(dim_x=3, # Размер вектора стостояния
dim_z=1) # Размер вектора измерений
# F - матрица процесса - размер dim_x на dim_x - 3х3
filter.F = np.array([ [1, dt, (dt**2)/2],
[0, 1.0, dt],
[0, 0, 1.0]])
# Матрица наблюдения - dim_z на dim_x - 1x3
filter.H = np.array([[1.0, 0.0, 0.0]])
# Ковариационная матрица ошибки модели
filter.Q = filterpy.common.Q_discrete_white_noise(dim=3, dt=dt, var=processNoiseVariance)
# Ковариационная матрица ошибки измерения - 1х1
filter.R = np.array([[measurementSigma*measurementSigma]])
# Начальное состояние.
filter.x = np.array([0.0, 0.0, 0.0])
# Ковариационная матрица для начального состояния
filter.P = np.array([[10.0, 0.0, 0.0],
[0.0, 10.0, 0.0],
[0.0, 0.0, 10.0]])
filteredState = []
stateCovarianceHistory = []
# Обработка данных
for i in range(0, len(measurement)):
z = [ measurement[i] ] # Вектор измерений
filter.predict() # Этап предсказания
filter.update(z) # Этап коррекции
filteredState.append(filter.x)
stateCovarianceHistory.append(filter.P)
filteredState = np.array(filteredState)
stateCovarianceHistory = np.array(stateCovarianceHistory)
# Визуализация
plt.title("Kalman filter (3rd order)")
plt.plot(measurement, label="Измерение", color="#99AAFF")
plt.plot(trajectory[0], label="Истинное значение", color="#FF6633")
plt.plot(filteredState[:, 0], label="Оценка фильтра", color="#224411")
plt.legend()
plt.show()
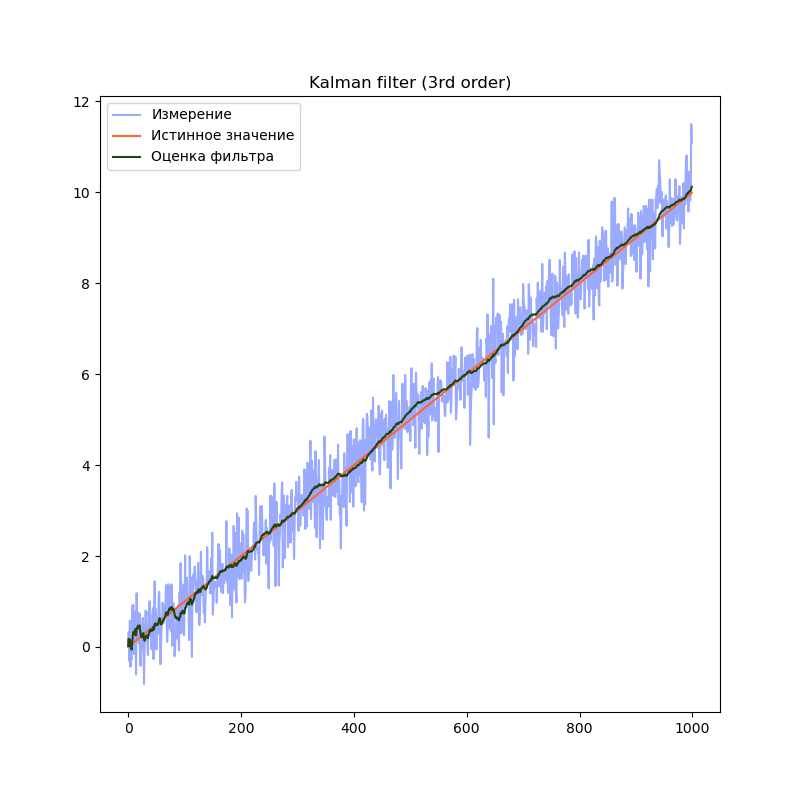
Бонус — сравнение различных порядков моделей
Сравним поведение фильтра с моделями разного порядка. Для начала, смоделируем более сложный сценарий поведения робота. Пусть робот находится в покое первые 20% времени, затем движется равномерно, а затем начинает двигаться равноускоренно:
Simulator.py
# Моделирование данных датчика
def simulateSensor(samplesCount, noiseSigma, dt):
# Шум с нормальным распределением. мат. ожидание = 0, среднеквадратичное отклонение = noiseSigma
noise = numpy.random.normal(loc = 0.0, scale = noiseSigma, size = samplesCount)
trajectory = np.zeros((3, samplesCount))
position = 0
velocity = 0.0
acceleration = 0.0
for i in range(1, samplesCount):
position = position + velocity * dt + (acceleration * dt ** 2) / 2.0
velocity = velocity + acceleration * dt
acceleration = acceleration
# Переход на равномерное движение
if(i == (int)(samplesCount * 0.2)):
velocity = 10.0
# Переход на равноускоренное движение
if (i == (int)(samplesCount * 0.6)):
acceleration = 10.0
trajectory[0][i] = position
trajectory[1][i] = velocity
trajectory[2][i] = acceleration
measurement = trajectory[0] + noise
return trajectory, measurement # Истинное значение и данные "датчика" с шумомВ предыдущем примере мы использовали модель, содержащую переменную (положение) и две производных её по времени (скорость и ускорение). Посмотрим, что будет, если избавиться от одной или обеих производных:
2-й порядок
# Создаём объект KalmanFilter
filter = filterpy.kalman.KalmanFilter(dim_x=2, # Размер вектора стостояния
dim_z=1) # Размер вектора измерений
# F - матрица процесса - размер dim_x на dim_x - 2х2
filter.F = np.array([ [1, dt],
[0, 1.0]])
# Матрица наблюдения - dim_z на dim_x - 1x2
filter.H = np.array([[1.0, 0.0]])
filter.Q = [[dt**2, dt],
[ dt, 1.0]] * processNoise
# Начальное состояние.
filter.x = np.array([0.0, 0.0])
# Ковариационная матрица для начального состояния
filter.P = np.array([[8.0, 0.0],
[0.0, 8.0]])
1-й порядок
# Создаём объект KalmanFilter
filter = filterpy.kalman.KalmanFilter(dim_x=1, # Размер вектора стостояния
dim_z=1) # Размер вектора измерений
# F - матрица процесса - размер dim_x на dim_x - 1х1
filter.F = np.array([ [1.0]])
# Матрица наблюдения - dim_z на dim_x - 1x1
filter.H = np.array([[1.0]])
# Ковариационная матрица ошибки модели
filter.Q = processNoise
# Ковариационная матрица ошибки измерения - 1х1
filter.R = np.array([[measurementSigma*measurementSigma]])
# Начальное состояние.
filter.x = np.array([0.0])
# Ковариационная матрица для начального состояния
filter.P = np.array([[8.0]])Сравним результаты:
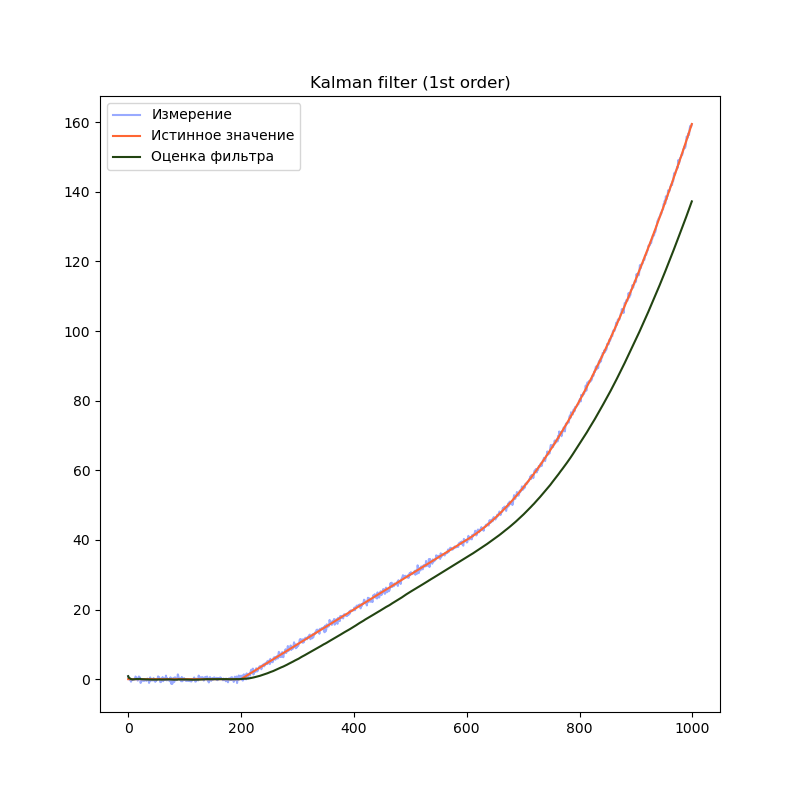
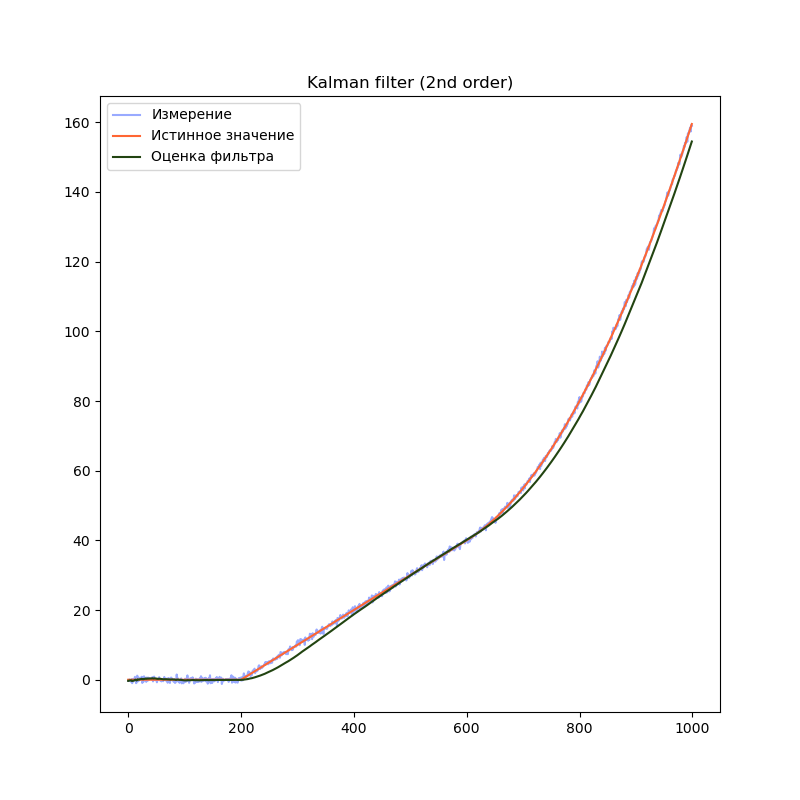

На графиках сразу заметно, что модель первого порядка начинает отставать от истинного значения на участках равномерного движения и равноускоренного движения. Модель второго порядка успешно справляется с участком равномерного движения, но так же начинает отставать на участке равноускоренного движения. Модель третьего порядка справляется со всеми тремя участками.
Однако, это не означает что нужно использовать модели высокого порядка во всех случаях. В нашем примере, модель третьего порядка справляется с участком равномерного движения несколько хуже модели второго порядка, т.к. фильтр интерпретирует шум сенсора как изменение ускорения. Это приводит к колебанию оценки фильтра. Стоит подбирать порядок модели в соответствии с планируемыми режимами работы фильтра.
Нелинейные модели и фильтр Калмана
Почему фильтр Калмана не работает для нелинейных моделей и что делать
Всё дело в нормальном распределении. При применении линейных преобразованийк нормально распределенной случайной величине, результирующее распределение будет представлять собой нормальное распределение, или будет пропорциональным нормальному распределению. Именно на этом принципе и строится математика фильтра Калмана.
Есть несколько модификаций алгоритма, которые позволяют работать с нелинейными моделями.
Например:
Extended Kalman Filter (EKF) — расширенный фильтр Калмана. Этот подход строит линейное приближение модели на каждом шаге. Для этого требуется рассчитать матрицу вторых частных производных функции модели, что бывает весьма непросто. В некоторых случаях, аналитическое решение найти сложно или невозможно, и поэтому используют численные методы.
Unscented Kalman Filter (UKF). Этот подход строит приближение распределения получающегося после нелинейного преобразования при помощи сигма-точек. Преимуществом этого метода является то, что он не требует вычисления производных.
Мы рассмотрим именно Unscented Kalman Filter
Unscented Kalman Filter и почему он без запаха
Основная магия этого алгоритма заключается в методе, который строит приближение распределения плотности вероятности случайной величины после прохождения через нелинейное преобразование. Этот метод называется unscented transform — сложнопереводимое на русский язык название. Автор этого метода, Джеффри Ульман, не хотел, чтобы его разработку называли “Фильтр Ульмана”. Согласно интервью, он решил назвать так свой метод после того как увидел дезодорант без запаха (“unscented deodorant”) на столе в лаборатории, где он работал.
Этот метод достаточно точно строит приближение функции распределения случайной величины, но что более важно — он очень простой.
Для использования UKF не придётся реализовывать какие-либо дополнительные вычисления, за исключением моделей системы. В общем виде, нелинейная модель не может быть представлена в виде матрицы, поэтому мы заменяем матрицы
Реализуем unscented Kalman filter для линейной модели из прошлого примера:
Код
import filterpy.kalman
import filterpy.common
import matplotlib.pyplot as plt
import numpy as np
import numpy.random
from Simulator import simulateSensor, CovarianceQ
dt = 0.01
measurementSigma = 0.5
processNoiseVariance = 1e-4
# Функция наблюдения - аналог матрицы наблюдения
# Преобразует вектор состояния x в вектор измерений z
def measurementFunction(x):
return np.array([x[0]])
# Функция процесса - аналог матрицы процесса
def stateTransitionFunction(x, dt):
newState = np.zeros(3)
newState[0] = x[0] + dt * x[1] + ( (dt**2)/2 ) * x[2]
newState[1] = x[1] + dt * x[2]
newState[2] = x[2]
return newState
trajectory, measurement = simulateSensor(1000, measurementSigma)
# Для unscented kalman filter необходимо выбрать алгоритм выбора сигма-точек
points = filterpy.kalman.JulierSigmaPoints(3, kappa=0)
# Создаём объект UnscentedKalmanFilter
filter = filterpy.kalman.UnscentedKalmanFilter(dim_x = 3,
dim_z = 1,
dt = dt,
hx = measurementFunction,
fx = stateTransitionFunction,
points = points)
# Ковариационная матрица ошибки модели
filter.Q = filterpy.common.Q_discrete_white_noise(dim=3, dt=dt, var=processNoiseVariance)
# Ковариационная матрица ошибки измерения - 1х1
filter.R = np.array([[measurementSigma*measurementSigma]])
# Начальное состояние.
filter.x = np.array([0.0, 0.0, 0.0])
# Ковариационная матрица для начального состояния
filter.P = np.array([[10.0, 0.0, 0.0],
[0.0, 10.0, 0.0],
[0.0, 0.0, 10.0]])
filteredState = []
stateCovarianceHistory = []
for i in range(0, len(measurement)):
z = [ measurement[i] ]
filter.predict()
filter.update(z)
filteredState.append(filter.x)
stateCovarianceHistory.append(filter.P)
filteredState = np.array(filteredState)
stateCovarianceHistory = np.array(stateCovarianceHistory)
plt.title("Unscented Kalman filter")
plt.plot(measurement, label="Измерение", color="#99AAFF")
plt.plot(trajectory[0], label="Истинное значение", color="#FF6633")
plt.plot(filteredState[:, 0], label="Оценка фильтра", color="#224411")
plt.legend()
plt.show()
Разница в коде минимальна. Мы заменили матрицы F и H на функции f(x) и h(x). Это позволяет использовать нелинейные модели системы и/или наблюдения:
# Функция наблюдения - аналог матрицы наблюдения
# Преобразует вектор состояния x в вектор измерений z
def measurementFunction(x):
return np.array([x[0]])
# Функция процесса - аналог матрицы процесса
def stateTransitionFunction(x, dt):
newState = np.zeros(3)
newState[0] = x[0] + dt * x[1] + ( (dt**2)/2 ) * x[2]
newState[1] = x[1] + dt * x[2]
newState[2] = x[2]
return newStateТакже, появилась строчка, устанавливающая алгоритм генерации сигма-точек
points = filterpy.kalman.JulierSigmaPoints(3, kappa=0)Этот алгоритм определяет точность оценки распределения вероятности при прохождении через нелинейное преобразование. К сожалению, существуют только общие рекомендации относительно генерации сигма-точек. Поэтому для каждой отдельной задачи значения параметров алгоритма подбираются экспериментальным путём.
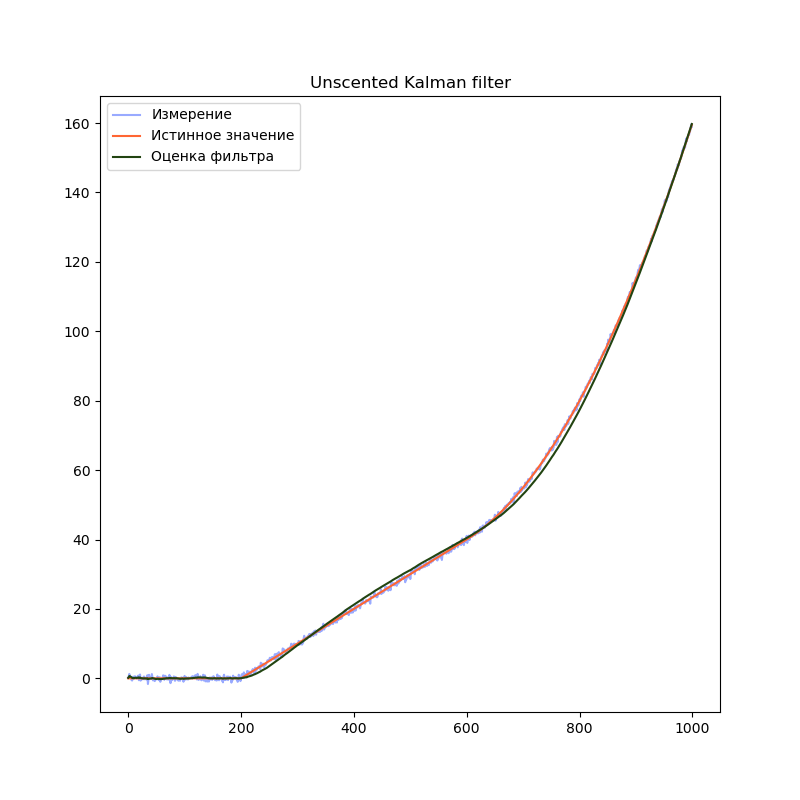
Ожидаемый результат — график оценки положения практически не отличается от обычного фильтра Калмана.
В этом примере используется линейная модель. Однако мы могли бы использовать нелинейные функции. Например, мы могли бы использовать следующую реализацию:
g = 9.8
# Вектор состояния - угол наклона
# Вектор измерений - ускорение вдоль осей X и Y
def measurementFunction(x):
measurement = np.zeros(2)
measurement[0] = math.sin(x[0]) * g
measurement[1] = math.cos(x[0]) * g
return measurementТакую модель измерений было бы невозможно использовать в случае с линейным фильтром Калмана
Вместо заключения
За рамками статьи остались теоретические основы фильтра Калмана. Однако объем материала по этой теме ошеломляет. Сложно выбрать хороший источник. Я бы хотел рекомендовать замечательную книгу от автора библиотеки filterpy Roger Labbe (на английском языке). В ней доступно описаны принципы работы алгоритма и сопутствующая теория. Книга представляет собой документ Jupyter notebook, который позволяет в интерактивном режиме экспериментировать с примерами.
Литература
→ Roger Labbe — Kalman and Bayesian Filters in Python
→ Wikipedia