Перевод поста Эда Пегга младшего (Ed Pegg Jr) "From Close to Perfect—A Triangle Problem"
Выражаю благодарность за помощь в переводе Андрею Дудину.
Скачать перевод в виде документа Mathematica, который содержит весь код использованный в статье, можно здесь.
В языке Wolfram Language (доступном, скажем, в системе Mathematica) функция RootApproximant позволяет найти замкнутую форму в виде алгебраического числа для некоторого приближённого числа, и эта функция позволила нам превратить приближенное решение задачи о разбиении квадрата на 50 подобных остроугольных треугольников с углами (45°, 60°, 75°) в точное.
Ясно, что квадрат можно разбить на треугольники (триангулировать), например, просто соединив его противоположные вершины. Известно, так же, что квадрат можно разбить на семь подобных треугольников разной площади или на десять остроугольных равнобедренных треугольников (см. рис. ниже). Известны также классические задачи, связанные с разбиением квадрата на восемь остроугольных треугольников (см. рис. ниже), или на двадцать треугольников со сторонами, относящимися друг к другу как
. На третьем чертеже (считая сверху) показано разбиение квадрата на подобные треугольники с углами (45°, 60°, 75°), но вы можете с легкостью заметить, что это решение не корректно, так как один из треугольников немного накладывается на другой.In[1]:=
Out[9]=
Можно с легкостью найти разбиение квадрата на подобные прямоугольные треугольники. Но можно ли найти разбиение квадрата на подобные не прямоугольные треугольники? В своей статье “Tilings of Polygons with Similar Triangles” (“Разбиение многоугольников на подобные треугольники”) (Combinatorica, 10(3), 1990 pp. 281–306), Ласкович (Laczkovich) доказал, что это возможно только для трёх видов треугольников с углами (22°30’, 45°, 112°30’), (15°, 45°, 120°) и (45°, 60°, 75°). Я прочёл эту статью и попытался найти в явном виде разбиение квадрата на подобные треугольники с углами (45°, 60°, 75°), но построение такого разбиения оказалось сложным, и у меня сложилось ощущение, что для решения этой задачи потребуется использовать тысячи таких треугольников. Во всех моих решениях присутствовали изъяны, аналогичные тому, что был показан выше, поэтому я решил организовать небольшое соревнование: награда за найденное разбиение равна 200 долларов минус доллар за каждый треугольник в найденном решении.
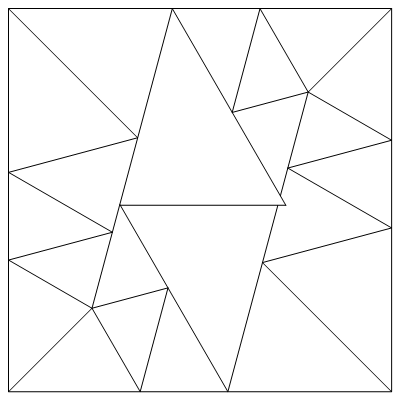
Лью Бакстер начал (Lew Baxter) с тщательного изучения подхода Ласковича, и смог найти решение, использовав для этого 7 триллионов треугольников. Но он нашёл способ улучшить это решение и написал программу для поиска более оптимальных решений. Уже через несколько недель он получил решение, содержащие 198 треугольников, чего было бы достаточно для того, чтобы получить от меня приз в размере 2 долларов. Но он продолжил свои поиски и наконец пришёл к решению содержащему всего 64 треугольника. К сожалению, координаты всех вершин треугольников были найдены приближённо, хотя и с большой точностью. На тот момент казалось, что решение, которое я привожу ниже, оптимально и найти лучшего решения, ещё и в замкнутой форме, не удастся. На рисунке ниже вы можете видеть найденное разбиение для половины квадрата, ясно, что достаточно отразить это решение относительно диагонали квадрата, чтобы получить решение исходной задачи.
In[10]:=
In[11]:=
In[12]:=
Out[12]=
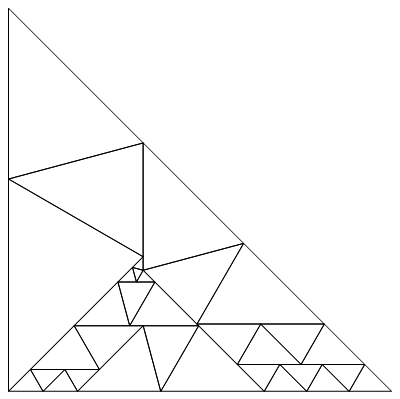
Для построения точного решения по этому приближённому решению можно использовать функцию RootApproximant, которая ищет корень некоторого многочлена, который будет с заданной точностью аппроксимировать данное приближённое число. В геометрических задачах, подобных той, что рассматриваем мы, очень часто точное решение как раз представляет собой набор корней некоторых многочленов. Для рассматриваемой задачи, я попробовал следующее: с помощью функции RootApproximant были найдены возможные замкнутые формы для каждой из координат, которые затем были умножены на 4686 для того, чтобы избавиться от дробей. Все значения, как легко заметить, имеют вид
, что кажется довольно обнадёживающим.In[13]:=
Out[13]=
Ниже можно посмотреть на полученное решение, содержащее 64 треугольника.
In[14]:=
Out[14]=
Затем, я получил новое сообщение от Лью — если поработать немного с треугольниками 6, 7, 21, и 22, то в итоге можно заменить семь треугольников всего на один.
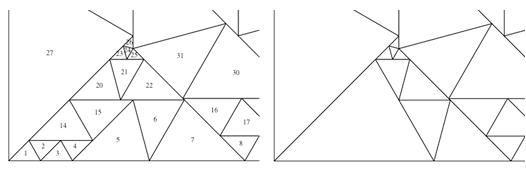
Я вычислил новый набор точных координат вершин, хотя это было уже не очень просто.
In[15]:=
In[16]:=
В итоге было получено решение, содержащее 50 треугольников. Неужели это точное решение? С помощью кода, приведённого ниже, вычислим углы всех треугольников.
In[17]:=
In[18]:=
Out[18]=
Легко видеть, что каждый из треугольников имеет углы, равные в точности (45°, 60°, 75°), так что решение Бакстера в действительности точное. Теперь мы можем взглянуть на решение содержащее 50 треугольников.
In[19]:=
Out[19]=
Таким образом, я должен Лью Бакстеру 150 долларов. Если вы когда-либо занимались проблемами численной оптимизации и поиск точного решения cложен и не понятен, возможно вам стоит попробовать использовать функции, вроде, RootApproximant в языке Wolfram Language.
