Комментарии 26
Спасибо за то, что почитали информацию из моего профиля) Я польщен вашим вниманием.
Поясню для вас немного: «первый» — относится ко времени появления сертифицированных инструкторов.
«Руководитель» — это не системный администратор (мою должность можно назвать с той же легкостью «IT-директор»).
Последнее: я не убеждаю никого в своей крутости) В статьях даже нет упоминания про меня (кроме небольшой строки внизу). Я рассказываю про интересные задачи, которые можно решать с помощью языка Wolfram Language, часть из которых решаю сам, а часть — являются переводами из официальных блогов и журналов Wolfram Research.
Поясню для вас немного: «первый» — относится ко времени появления сертифицированных инструкторов.
«Руководитель» — это не системный администратор (мою должность можно назвать с той же легкостью «IT-директор»).
Последнее: я не убеждаю никого в своей крутости) В статьях даже нет упоминания про меня (кроме небольшой строки внизу). Я рассказываю про интересные задачи, которые можно решать с помощью языка Wolfram Language, часть из которых решаю сам, а часть — являются переводами из официальных блогов и журналов Wolfram Research.
Есть такие конструкторы для создания многогранников.

Я так понял, для 6, 7, 8, 9 и 16 автор нашел глобальный оптимум, а для остальных — просто хорошие решения (пока не понятно глобальный это оптимум или нет). И что оптимальность следует из существования некого root object.
Кто-нибудь на пальцах может объяснить что такое root object и как оно доказывает, что решение оптимально?
Кто-нибудь на пальцах может объяснить что такое root object и как оно доказывает, что решение оптимально?
Root object — это специальная конструкция в языке Wolfram Language, основанная на функции Root.
Root[f, k] задает k-й корень полиномиального уравнения f[x]=0.
Этот символьный объект является аналитическим и Wolfram Language может производить множество различных вычислений, опираясь на его свойства. Эти объекты служат для представления решений полиномиальных уравнений степени выше 4-й, которые по теореме Абеля — Руффини не могут быть решены в радикалах. Если посмотрите на решение Эда Пега, вы увидите и полином f и номер корня k. Полином представляется в виде чистой функции с аргументом #1 (аналог x, по сути).
Простой пример:

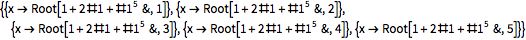
Root[f, k] задает k-й корень полиномиального уравнения f[x]=0.
Этот символьный объект является аналитическим и Wolfram Language может производить множество различных вычислений, опираясь на его свойства. Эти объекты служат для представления решений полиномиальных уравнений степени выше 4-й, которые по теореме Абеля — Руффини не могут быть решены в радикалах. Если посмотрите на решение Эда Пега, вы увидите и полином f и номер корня k. Полином представляется в виде чистой функции с аргументом #1 (аналог x, по сути).
Простой пример:

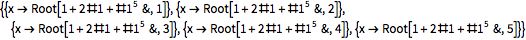
Ладно, хорошо, теперь это понятно. Теперь я даже вижу в статье полиномы с дикими коэффициентами. А откуда берутся эти полиномы и как они соотносятся с многогранниками? И почему в полиноме 16 степени мы берем именно 5й корень, их же там целых 16? Желательно тоже на пальцах, если не затруднит.
Еще в тексте фигурирует некий параметр r, но определения того, что это такое, я в статье не нашел.
Еще в тексте фигурирует некий параметр r, но определения того, что это такое, я в статье не нашел.
Как бы то ни было
-3 < 1, но (-3)^2 > 1.
Перевод совсем не ОК, лучше «для четырёх точек решением будет правильный тетраэдр». Так как мы фиксируем точки и ищем решение, а не наоборот.
Тут перевод даже не близок к оригиналу, там:
Где вы увидели пирамиду? Тут рассказано про конструкцию по ссылке [1], где берутся два «перпендикулярных» симлекса на трёх и на двух вершинах с единичными сторонами и рассматривается их выпуклая оболочка.
Возведение числа в квадрат, которое больше или меньше единицы, даст большее или меньшее число соответственно.
-3 < 1, но (-3)^2 > 1.
Для правильного тетраэдра с объёмом в sqrt(2)/12= 0.117851 потребуется четыре точки.
Перевод совсем не ОК, лучше «для четырёх точек решением будет правильный тетраэдр». Так как мы фиксируем точки и ищем решение, а не наоборот.
Для правильной пирамиды с единичным перпендикуляром потребуется 5 точек, а её объём равен sqrt(3)/12 = 0.1443375; это решение было получено в 1976-ом году [1].
Тут перевод даже не близок к оригиналу, там:
Five points need a unit equilateral triangle with a perpendicular unit line, with volume Square root of 3/12 = 0.1443375; solved in 1976 [1].
Где вы увидели пирамиду? Тут рассказано про конструкцию по ссылке [1], где берутся два «перпендикулярных» симлекса на трёх и на двух вершинах с единичными сторонами и рассматривается их выпуклая оболочка.
Вы можете говорить что угодно, это ваше личное субъективное мнение, высказанное в классической манере интернет-хама. Единственное ваше желание — хамить, спровоцировать на ответную негативную реакцию. Именно поэтому вы пишите брызжущие слюной комментарии, в отличие от, скажем, mkot, указавшего выше на конкретные огрехи нашего с Кириллом перевода, которые мы исправим. У вас ничего не получится, можете не стараться, меня из себя вы не выведите)
Если по-честному, то ваши переводы действительно требуют серьёзной доработки.
Вот наугад взял:
Что-такое огромный ромбокубоктаэдр? В оригинале great rhombcuboctahedron. Слова great и small рядом с телами обычно переводят как большой и малый. Дальше, почему половина тела? На что это должно быть похоже? Снова в оригинале было half the vertices of. То есть особым образом выбранная половина вершин. И т. п.
На самом деле ваши статьи гораздо бы улучшились и их бы стало приятнее читать, если бы их кто-нибудь, кто хорошо разбирается в теме, вычитал бы перед публикацией.
Вот наугад взял:
половина огромного ромбокубоктаэдра
Что-такое огромный ромбокубоктаэдр? В оригинале great rhombcuboctahedron. Слова great и small рядом с телами обычно переводят как большой и малый. Дальше, почему половина тела? На что это должно быть похоже? Снова в оригинале было half the vertices of. То есть особым образом выбранная половина вершин. И т. п.
На самом деле ваши статьи гораздо бы улучшились и их бы стало приятнее читать, если бы их кто-нибудь, кто хорошо разбирается в теме, вычитал бы перед публикацией.
Вы видимо знаете мою биографию лучше меня. Если вы считаете себя великим математиком, напишите статью, покажите сами класс) А то, насколько я вижу, вы только занимаетесь критиканством других, прячась за своей анонимной страничкой, не содержащей никакой информации о вас. Приведите свою оф. страницу, список ваших опубликованных работ, должность, организацию, фото, ваш город и пр., чтобы мы могли оценить ваш уровень профессионализма. Информация обо мне представлена наиболее полно в LinkedIn (за исключением последней должности в Баласс, которая еще не описана) ru.linkedin.com/in/osipovroman
Ок, аноним brainick.
P.S. Потрудитесь почитать мой профиль дальше первой строчки.
P.S. Потрудитесь почитать мой профиль дальше первой строчки.
Утомили вы меня уже выцеплять только удобные вам куски, чтобы выдрав их из общего контекста и содержания подать так, как вам нужно.
Если бы вы потрудились погуглить, вы бы нашли, что это за общество «Женщины в науке и образовании», организующее ежегодную международную конференцию «Математика. Компьютер. Образование» www.mce.biophys.msu.ru при поддержке огромного количества уважаемых организаций и деятелей науки и образования. Если вы думаете, что такой умный и пошутили о названии этой организации первым — о, вы сильно ошибаетесь.
Что касается кандидатской — я никогда не говорил, что она была защищена и что у меня есть к. ф-м. н.
Мое общение на этом с вами окончено. На дальнейшие комментарии с вашей стороны отвечать не буду, потому что смысла тратить на вас время, объясняя кто я и чем занимаюсь — не вижу вообще.
Распинаться перед интернет-троллем-анонимом у меня желания больше нет. Удачи.
Если бы вы потрудились погуглить, вы бы нашли, что это за общество «Женщины в науке и образовании», организующее ежегодную международную конференцию «Математика. Компьютер. Образование» www.mce.biophys.msu.ru при поддержке огромного количества уважаемых организаций и деятелей науки и образования. Если вы думаете, что такой умный и пошутили о названии этой организации первым — о, вы сильно ошибаетесь.
Что касается кандидатской — я никогда не говорил, что она была защищена и что у меня есть к. ф-м. н.
Мое общение на этом с вами окончено. На дальнейшие комментарии с вашей стороны отвечать не буду, потому что смысла тратить на вас время, объясняя кто я и чем занимаюсь — не вижу вообще.
Распинаться перед интернет-троллем-анонимом у меня желания больше нет. Удачи.
А со мной вы будете разговаривать?
Мне кажется, вы слишком строги к Роману и выставляете слишком высокую планку для публикуемой здесь информации. Насколько я могу судить, Хабр не является научной площадкой. Учитывая, что авторство статей (тех, о которых идет речь) принадлежит не Роману, критиковать можно две вещи: качество перевода и процесс отбора информации. По переводу, насколько я вижу, Роман принимает и учитывает замечания. По отбору — в конце концов, это его дело.
Я понимаю ваше стремление увеличить плотность информации и отношение сигнал / шум, но на таких ресурсах как Хабр, мне думается, это lost cause (да и вообще, задача совсем не из простых, и в первую очередь должна решаться создателями площадки, а не блоггерами, на таких площадках как Хабр). Я мог бы перечислить несколько причин, почему это так (как мне представляется), но скажу лишь, что, по моему мнению, это прямо заложено в бизнес и социальную модель Хабра и вполне устраивает его создателей. Это вполне в духе времени, нравится это или нет. Пытаться превратить площадку в то, чем она не является — неблагодарный труд. В конце концов, никто не мешает попробовать организовать площадку, где будут действовать другие правила, и сделать ее успешной и посещаемой.
Возвращаясь к постам этого блога, я бы посоветовал в первую очередь рассматривать их как иллюстрации к применению функционала Wolfram Mathematica, рассчитанные на широкую (и потому разно-уровневую, и в целом не очень взыскательную) аудиторию. Есть два подхода к подаче информации: можно либо предоставлять много разного и давать каждому возможность решать, что ценно, а что нет, либо давать «избранное», но тогда отбирающий во-многом принимает решение за читателя. И раз уж вы заговорили об отечественной науке, то позвольте мне, как человеку имевшему дело и с отечественным, и с зарубежным подходом, сказать вот что: во-многом, именно отсутствие упора на «единственном правильном пути к истине» помогает западным ученым выходить на высокий уровень и получать замечательные результаты (сравните, например, лекции Фейнмана с курсом Ландау, для начинающего физика-теоретика).
Мне кажется, вы слишком строги к Роману и выставляете слишком высокую планку для публикуемой здесь информации. Насколько я могу судить, Хабр не является научной площадкой. Учитывая, что авторство статей (тех, о которых идет речь) принадлежит не Роману, критиковать можно две вещи: качество перевода и процесс отбора информации. По переводу, насколько я вижу, Роман принимает и учитывает замечания. По отбору — в конце концов, это его дело.
Я понимаю ваше стремление увеличить плотность информации и отношение сигнал / шум, но на таких ресурсах как Хабр, мне думается, это lost cause (да и вообще, задача совсем не из простых, и в первую очередь должна решаться создателями площадки, а не блоггерами, на таких площадках как Хабр). Я мог бы перечислить несколько причин, почему это так (как мне представляется), но скажу лишь, что, по моему мнению, это прямо заложено в бизнес и социальную модель Хабра и вполне устраивает его создателей. Это вполне в духе времени, нравится это или нет. Пытаться превратить площадку в то, чем она не является — неблагодарный труд. В конце концов, никто не мешает попробовать организовать площадку, где будут действовать другие правила, и сделать ее успешной и посещаемой.
Возвращаясь к постам этого блога, я бы посоветовал в первую очередь рассматривать их как иллюстрации к применению функционала Wolfram Mathematica, рассчитанные на широкую (и потому разно-уровневую, и в целом не очень взыскательную) аудиторию. Есть два подхода к подаче информации: можно либо предоставлять много разного и давать каждому возможность решать, что ценно, а что нет, либо давать «избранное», но тогда отбирающий во-многом принимает решение за читателя. И раз уж вы заговорили об отечественной науке, то позвольте мне, как человеку имевшему дело и с отечественным, и с зарубежным подходом, сказать вот что: во-многом, именно отсутствие упора на «единственном правильном пути к истине» помогает западным ученым выходить на высокий уровень и получать замечательные результаты (сравните, например, лекции Фейнмана с курсом Ландау, для начинающего физика-теоретика).
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
Наибольшие малые многогранники: новые решения в комбинаторной геометрии