Комментарии 14
Ну как всегда, на самом интересном месте…
www.youtube.com/watch?v=p8zPx41oxwE
www.youtube.com/watch?v=eyNhhRCCMiI
Познавательные видео, давно смотрел и не раз, очень наглядно.
www.youtube.com/watch?v=eyNhhRCCMiI
Познавательные видео, давно смотрел и не раз, очень наглядно.
Минутку-минутку! Я вот смотрел видео, как вывернуть сферу наизнанку (Chijikson приложил ссылки на две части), и там нельзя было выполнять такое преобразование, как вот у вас тут:
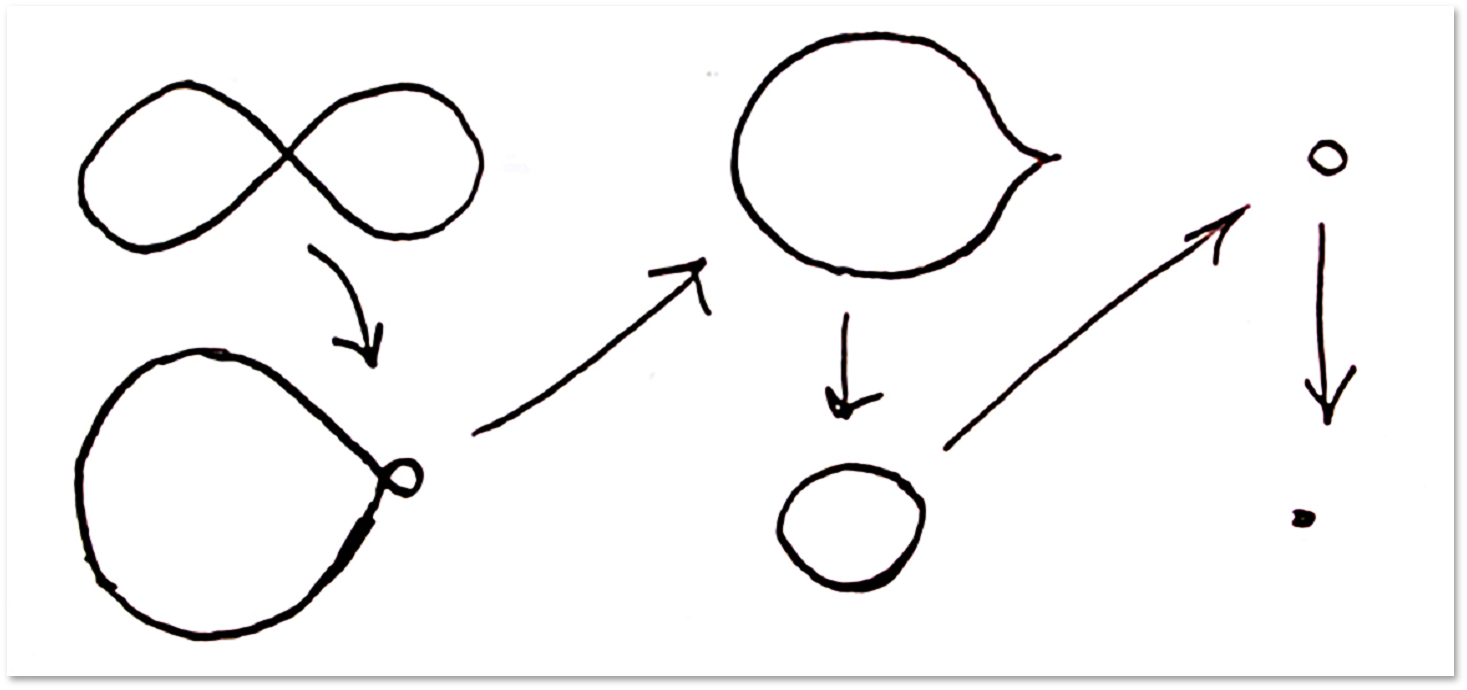
Разве изломы допустимы? Или это зависит, простите дилетанта, от уровня «строгости»?
Ну и к превращению сферы в полусферу такой же вопрос — если у краев получившейся «миски» конечная кривизна, т.е. это не излом, то тогда это и не полусфера, а если края являются именно изломами — то было ли корректным такое преобразование?

Разве изломы допустимы? Или это зависит, простите дилетанта, от уровня «строгости»?
Ну и к превращению сферы в полусферу такой же вопрос — если у краев получившейся «миски» конечная кривизна, т.е. это не излом, то тогда это и не полусфера, а если края являются именно изломами — то было ли корректным такое преобразование?
Излома нет. Эту восьмерку можно нарисовать касательными, т.е. два круга соприкасающиеся в точке.
В парадоксе Смейла (видео про сферу) речь идет о так называемой регулярной гомотопии. Требование гладкости (отсутствия изломов) для регулярной гомотопии вытекает ровно из того факта, что оно дает интересные для изучения классы погружений.
В данном случае рассматривается вполне обычная гомотопия петель, которая которая определяет гомотопические классы и, соответственно, фундаментальную группу. Такая конструкция опять же рассматривается ровно потому, что она дает интересную информацию о структуре — позволяет классифицировать многообразия.
Надо понимать, что нет никакого «высшего смысла» в изучении какого-либо конкретного типа гомотопий или каких-либо объектов вообще. Их изучают ровно потому, что они интересны. Каждый из них имеет свое право на существование (но фундаментальная группа, в некотором смысле, более фундаментальна).
В данном случае рассматривается вполне обычная гомотопия петель, которая которая определяет гомотопические классы и, соответственно, фундаментальную группу. Такая конструкция опять же рассматривается ровно потому, что она дает интересную информацию о структуре — позволяет классифицировать многообразия.
Надо понимать, что нет никакого «высшего смысла» в изучении какого-либо конкретного типа гомотопий или каких-либо объектов вообще. Их изучают ровно потому, что они интересны. Каждый из них имеет свое право на существование (но фундаментальная группа, в некотором смысле, более фундаментальна).
[offtop]
О Перельмане есть довольно интересный документальный фильм, называется: «Иноходец. Урок Перельмана». Советую посмотреть.
[/offtop]
О Перельмане есть довольно интересный документальный фильм, называется: «Иноходец. Урок Перельмана». Советую посмотреть.
[/offtop]
Огромное спасибо Яндексу (и всем преподавателям в частности) за интересные лекции, а также комментаторам за полезные ссылки.
Я ничего не имею против математики, даже за её развитие, но мне тяжело понимать некоторые вещи. Например, то, какое практическое применение носит теорема Пуанкаре.
За видео спасибо!
За видео спасибо!
Практическая польза такая же, как и от Гипотеза Таниямы — Симуры — Вейля. Развитие фундаментальной науки прежде всего.
Это где-то крутилось в голове, но я немного о другом спрашивал. Наверное не верно сформулировал вопрос. Я хотел узнать, нашло ли доказательство данной гипотезы, применение где-нибудь в практике, в уже существующих технологиях. Т.е. такое событие очень пригодилось кому-то прямо здесь и сейчас, просто раньше на гипотезу лишь ссылались, а теперь можно быть уверенным в её верности.
О как…
Фёдор Юрьевич на хабре o_0
Фёдор Юрьевич на хабре o_0
Очень интересно, спасибо.
Есть одна маленькая просьба: захватывайте лазерную указку и отправляйте её на правую сторону экрана. Для этого нужна веб-камера с ИК фильтром и несложная програмка.
Есть одна маленькая просьба: захватывайте лазерную указку и отправляйте её на правую сторону экрана. Для этого нужна веб-камера с ИК фильтром и несложная програмка.
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
О гипотезе Пуанкаре. Лекция в Яндексе