Это вторая часть статьи о том, как улучшить A/B-тесты. Советую сначала прочитать первую, чтобы лучше понимать материал. В новой части я подробно остановлюсь на методах увеличения мощности в A/B-тестах: поговорим про CUPED, бутстрап-критерии, стратификацию и парную стратификацию.

Терминология
Ещё раз напомню терминологию, которую буду использовать в статье:
Статистически значимый результат — результат, который статистически значимо лучше 0.
Прокрас теста — результат эксперимента статистически значимо отличается от 0, и у вас есть какой-то эффект.
Зелёный тест — метрика в A/B-тесте статистически значимо стала лучше.
Красный тест — метрика в A/B-тесте статистически значимо стала хуже.
Серый тест — результат A/B-теста не статистически значим.
Тритмент — фича или предложение, чьё воздействие на пользователей вы проверяете в A/B-тесте.
MDE — минимальный детектируемый эффект. Размер, который должен иметь истинный эффект от тритмента, чтобы эксперимент его обнаружил с заданной долей уверенности (мощностью). Чем меньше MDE, тем лучше.
Мощность критерия — вероятность критерия задетектировать эффект, если он действительно есть. Чем больше мощность критерия, тем он круче. Мощность также напрямую зависит от ширины доверительного интервала: чем она меньше, тем мощнее критерий.
Предпериод — период до начала эксперимента.
Методы увеличения мощности в AB-тестах
Для начала давайте вспомним, из каких 3 основных этапов состоит AB–тест:
Разделение пользователей на тест и контроль.
Активная стадия теста. Пользователи совершают действия, которые мы потом будем анализировать.
Анализ результатов. Здесь применяются статистические критерии для подведения итогов теста.
Каждый из этих этапов можно улучшить.
Увеличение времени продолжительности теста
Начнём с самого простого метода увеличить мощности A/B-теста: увеличить время продолжительности теста. В основном, чем дольше вы держите тест, тем вероятнее получите статистически значимые результаты, потому что в эксперименте поучаствует больше людей. Чем больше людей, тем меньше дисперсия у средних величин, а значит, меньше доверительный интервал. Это увеличивает вероятность задетектировать эффект.
Но чем больше вы держите тест, тем меньше гипотез протестируете за определённый промежуток времени. Например:
Вы держите один тест два месяца и не можете запустить другой тест, который влияет на результаты текущего эксперимента.
Вы держите один тест один месяц, а во второй месяц запускаете второй эксперимент.
В первом случае доверительный интервал при анализе первого теста будет поменьше, чем во втором. Зато во втором случае вы смогли протестировать сразу две гипотезы.

Но даже если вы захотите продержать тест два года, не факт, что мощность критерия будет сильно лучше, чем если бы вы держали его год. У нас часто бывает, что людей становится больше, но и метрика в этот момент становится шумнее. Из-за этого не происходит сокращения доверительного интервала. Рассмотрим пример: для одного из наших A/B-экспериментов я построил зависимость ширины доверительного интервала от номера недели эксперимента.
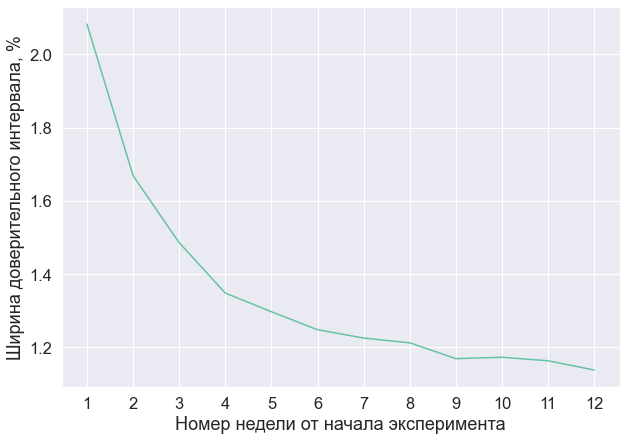
Здесь видно, что в последние шесть недель доверительный интервал особо не менялся, а значит, не менялась и мощность критерия. Поэтому не важно, в какую из последних недель я проводил бы анализ: в мощности A/B-теста я бы не выигрывал. Но если бы я подержал эксперимент только шесть недель, то во вторые шесть бы мог запустить другой эксперимент и не потерять в мощности для первого.
Кстати, построив такой график на предэкспериментальном периоде, вы можете определить оптимальный срок A/B-теста. Как это сделать:
Например, вы планируете запустить тест 1 июня. Вы берёте значение метрики для пользователя
С 1 по 8 марта.
С 1 по 15 марта.
...
С 1 марта по 31 мая.
Делите случайно в каждом примере выше пользователей на тест и контроль.
Запускаете на них ваш критерий. Считаете ширину доверительного интервала.
Рисуете график как в примере выше.
Определяете срок A/B-теста.
Таким образом вы сможете определить оптимальный срок, чтобы не проводить тест слишком долго и не потерять в мощности критерия.
Замечание: эти рассуждения корректны, если вы не измеряете долгосрочные эффекты от тритмента. В противном случае стоит как можно дольше держать эксперимент.
Итого: увеличение времени проведения — часто рабочий метод улучшить мощность A/B-теста, но лишь до определённого срока. Кроме того, это ограничивает скорость тестирования гипотез.
Перейдём к более интересной и всегда рабочей схеме: методам сокращения дисперсии при постанализе A/B-теста. Самый простой, но и самый опасный способ, — убрать выбросы или топ пользователей. Но это мы уже обсудили в предыдущей статье. Теперь я предлагаю посмотреть, как создать более мощные критерии, не изменяя выборку.
Постанализ: CUPED
CUPED (Controlled-experiment Using Pre-Experiment Data) — очень популярный в последнее время метод уменьшения вариации. Основная идея метода такова: давайте вычтем что-то из теста и из контроля так, чтобы математическое ожидание разницы новых величин осталось таким же, как было, а дисперсия уменьшилась.

A и B — некоторые случайные величины (ковариаты). Тогда утверждается, что если θ будет такой, как указано в формулах далее, то дисперсия будет минимально возможной для таких статистик:

В случае выборок разного размера:

Формула для дисперсии:


То есть, чем больше корреляция по модулю, тем меньше будет дисперсия.
Также важно помнить: чтобы метод работал корректно, необходимо и достаточно, чтобы математические ожидания A и B совпадали.

Осталось понять, что брать в роли A и B. Чаще всего для них берут значения той же метрики на предэкспериментальном периоде. Например, вы смотрите метрику выручки, тогда в роли ковариаты A и B можно взять выручку от пользователя за месяц до начала эксперимента. Чем хорош такой способ:
Математическое ожидание метрики на предпериоде будет одним и тем же в тесте и в контроле — иначе у вас некорректно поставлен A/B-тест. А значит, и CUPED даст правильный результат.
В большинстве случаев метрика на предпериоде сильно коррелирует с экспериментальным периодом. Отсюда получается, что и дисперсия сильно уменьшится.
Кроме значения метрики на предпериоде можно использовать результаты ML-модели, обученной предсказывать истинные значения метрик без влияния тритмента. С хорошей моделью можно достичь большего уменьшения дисперсии.
Теперь, когда мы определились с новой метрикой, надо понять, какой критерий использовать. Можно точно также использовать T-test для CUPED-метрик. Вот результаты проверок на искусственных тестах:
Проверка корректности метода на AB, AA тестах
# 2. Создание тестируемого критерия.
def cuped_ttest(control, test, control_before, test_before):
theta = (np.cov(control, control_before)[0, 1] + np.cov(test, test_before)[0, 1]) /\
(np.var(control_before) + np.var(test_before))
control_cup = control - theta * control_before
test_cup = test - theta * test_before
return absolute_ttest(control_cup, test_cup)
# 3. Заводим счётчик.
bad_cnt = 0
# 4. Цикл проверки.
N = 30000
for i in tqdm_notebook(range(N)):
# 4.a. Тестирую A/B-тест.
control_before = sps.expon(scale=1000).rvs(1000)
control = control_before + sps.norm(loc=0, scale=100).rvs(1000)
test_before = sps.expon(scale=1000).rvs(1000)
test = test_before + sps.norm(loc=0, scale=100).rvs(1000)
test *= 1.1
# 4.b. Запускаю критерий.
_, _, _, left_bound, right_bound = cuped_ttest(control, test, control_before, test_before)
# 4.c. Проверяю, лежит ли истинная разница средних в доверительном интервале.
if left_bound > 100 or right_bound < 100:
bad_cnt += 1
# 5. Строю доверительный интервал для конверсии ошибок у критерия.
left_real_level, right_real_level = proportion_confint(count = bad_cnt, nobs = N, alpha=0.05, method='wilson')
# Результат.
print(f"Реальный уровень значимости: {round(bad_cnt / N, 4)};"
f" доверительный интервал: [{round(left_real_level, 4)}, {round(right_real_level, 4)}]")Реальный уровень значимости: 0.0513; доверительный интервал: [0.0489, 0.0539].
Результаты для A/A-тестов: реальный уровень значимости: 0.0486; доверительный интервал: [0.0462, 0.0511].
Про используемую процедуру проверки критерия можно прочитать в первой части статьи.
Давайте ещё посмотрим, на сколько в искусственном примере уменьшилась ширина доверительного интервала по сравнению с обычным T-test:
# 2. Создание тестируемого критерия.
def cuped_ttest(control, test, control_before, test_before):
theta = (np.cov(control, control_before)[0, 1] + np.cov(test, test_before)[0, 1]) /\
(np.var(control_before) + np.var(test_before))
control_cup = control - theta * control_before
test_cup = test - theta * test_before
return absolute_ttest(control_cup, test_cup)
cuped_ci_lengths = []
ttest_ci_lengths = []
N = 30000
for i in tqdm_notebook(range(N)):
# 4.a. Тестирую A/B-тест.
control_before = sps.expon(scale=1000).rvs(1000)
control = control_before + sps.norm(loc=0, scale=100).rvs(1000)
test_before = sps.expon(scale=1000).rvs(1000)
test = test_before + sps.norm(loc=0, scale=100).rvs(1000)
test *= 1.1
# 4.b. Запускаю критерий.
_, _, cuped_ci, _, _ = cuped_ttest(control, test, control_before, test_before)
_, _, ttest_ci, _, _ = absolute_ttest(control, test)
cuped_ci_lengths.append(cuped_ci)
ttest_ci_lengths.append(ttest_ci)
coeff = np.mean(cuped_ci_lengths) / np.mean(ttest_ci_lengths)
print(f"Отношение ширины доверительных интервалов друг к другу: {round(coeff * 100, 3)}%")Отношение ширины доверительных интервалов друг к другу: 11.015%.
Мы сократили доверительный интервал примерно в 10 раз! В этом примере мы очень сильно увеличили мощность критерия, перейдя от T-test к CUPED-критерию. А ещё, CUPED состоит всего из четырёх строчек кода!
Также, часто в некоторых статьях предлагают следующую метрику для CUPED:

Вместо ковариаты B, объявленной ранее, подставляется значение этой метрики на предпериоде, из которого вычтено среднее значение. Тогда математическое ожидание этой ковариаты будет нулевым, а математическое ожидание новых штрихованных метрик совпадает с математическим ожиданием начальных метрик:

Кроме того, в этот момент вы не теряете бизнес-смысл у вашей новой CUPED-метрики, и можете посчитать оценки и доверительные интервалы для вашей метрики в тесте и в контроле.
Так вот, запомните: никогда не используйте такую CUPED–метрику! Покажу, к чему это может привести.
Пример
Сначала посмотрим, сколько раз истинное математическое ожидание C не попало в доверительный интервал для математического ожидания C'':
bad_cnt = 0
N = 1000
for i in tqdm_notebook(range(N)):
control_before = sps.expon(scale=1000).rvs(1000)
control = control_before + sps.norm(loc=0, scale=100).rvs(1000)
control_cup = control - (control_before - np.mean(control_before))
std = np.std(control_cup) / np.sqrt(len(control_cup))
mean = np.mean(control_cup)
left_bound, right_bound = sps.norm(loc=mean, scale=std).ppf([0.025, 0.975])
if left_bound > 1000 or right_bound < 1000:
bad_cnt += 1
left_real_level, right_real_level = proportion_confint(count = bad_cnt, nobs = N, alpha=0.05, method='wilson')
print(f"Не попал в {round(bad_cnt / N, 4) * 100}% случаев;"
f" доверительный интервал: [{round(left_real_level, 4) * 100}%, {round(right_real_level, 4) * 100}%]")Не попал в 85.2% случаев; доверительный интервал: [82.86%, 87.27%].
Новая метрика имеет другое математическое ожидание, нежели изначальная (в тех предпосылках, на которых работает t-test и на которых строится доверительный интервал через ЦПТ)! Это значит, что вы не можете использовать доверительный интервал этой статистики для оценки среднего у начальной метрики.
А теперь посмотрим, что в этот момент покажет CUPED-критерий:
# 2. Создание тестируемого критерия.
def incorrect_cuped(control, test, control_before, test_before):
theta = (np.cov(control, control_before)[0, 1] + np.cov(test, test_before)[0, 1]) /\
(np.var(control_before) + np.var(test_before))
control_mean = np.mean(control_before)
test_mean = np.mean(test_before)
control_cup = control - theta * (control_before - control_mean)
test_cup = test - theta * (test_before - test_mean)
return absolute_ttest(control_cup, test_cup)
# 4. Цикл проверки.
N = 30000
for i in tqdm_notebook(range(N)):
# 4.a. Тестирую A/A-тест.
control_before = sps.expon(scale=1000).rvs(1000)
control = control_before + sps.norm(loc=0, scale=100).rvs(1000)
test_before = sps.expon(scale=1000).rvs(1000)
test = test_before + sps.norm(loc=0, scale=100).rvs(1000)
# 4.b. Запускаю критерий.
_, _, _, left_bound, right_bound = incorrect_cuped(control, test, control_before, test_before)
# 4.c. Проверяю, лежит ли истинная разница средних в доверительном интервале.
if left_bound > 0 or right_bound < 0:
bad_cnt += 1
# 5. Строю доверительный интервал для конверсии ошибок у критерия.
left_real_level, right_real_level = proportion_confint(count = bad_cnt, nobs = N, alpha=0.05, method='wilson')
# Результат.
print(f"Реальный уровень значимости: {round(bad_cnt / N, 4)};"
f" доверительный интервал: [{round(left_real_level, 4)}, {round(right_real_level, 4)}]")Реальный уровень значимости: 0.8964; доверительный интервал: [0.8929, 0.8998].
Ошибка будет больше, чем в 80% случаев!
Получается, что метрика как портит CUPED-критерий, так и не даёт правильную оценку изначальной метрики.
> Доказательство и выводы из него
Давайте вспомним, в каком предположении работает T-test, а также строится доверительный интервал для случайной величины по выборке? В предположении о независимости элементов, где как раз и кроется ошибка. Давайте немного поколдуем.
Возьмём случайную величину mean(C_b) и размножим её на выборку размера N, что мы и делаем в рассматриваемой CUPED-метрике. Посчитаем математическое ожидание и дисперсию выборки в предположении о независимости её элементов.
В таком случае дисперсия будет равна 0, ведь вся выборка состоит только из одного значения.
Математическое ожидание: вне зависимости от размера N, среднее у этой выборки будет равно mean(C_b), а значит, по усиленному закону больших чисел математическое ожидание выборки будет равно текущему полученному значению mean(C_b), а не истинному матожиданию C_b.
Думаю, вы поняли, к чему я клоню. В предположении о независимости выборок получаются следующие результаты:
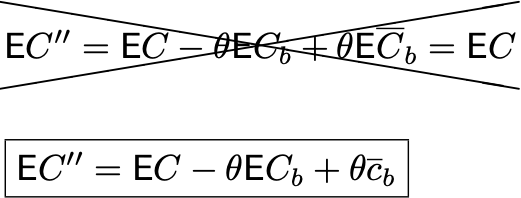
Где c_b — полученное значение среднего на предпериоде.
То есть алгоритм построения доверительного интервала, а также T-test ожидают получить на вход такую выборку:

Где различные индексы отвечают за разные наблюдения. А мы вместо этого передаём такую выборку, внимание на индекс у mean(C_b):

Поэтому и возникает продемонстрированная ранее ошибка.
Итого: в предположении о независимости, CUPED-метрика с вычитанием среднего значения приведёт вас к неверному результату! А зависимость элементов выборки очевидно следует из того, что у вас используется одна и та же случайная величина при создании каждого элемента выборки.
Теперь, посмотрим, как решить этот вопрос:
Не использовать такую CUPED-метрику.
Намучиться, пострадать, но самостоятельно выписать дисперсию для среднего этой метрики, учитывая все ковариации и зависимости в данных. Возможно, получится корректный критерий, если вы не ошибётесь.
Реализовать через бутстрап. И тогда подобная ковариата работает.
Причём варианты два и три не несут в себе глубокого смысла, потому что по мощности их критерии не будут выигрывать у аналогов без вычитания среднего.

Относительный CUPED
Осталось показать, как настроить CUPED для относительной постановки A/B-тестов. И здесь всё будет не так гладко.
Предлагается посмотреть на следующую нетривиальную статистику:

Причём в числителе штрихованные CUPED — случайные величины без вычитания среднего у ковариаты, а в знаменателе — обычное среднее на контроле, без штрихов. Знаменатель такой, потому что CUPED-метрика не сохранит изначальное математическое ожидание.
Утверждается, что при большом размере выборок эта статистика, как и относительный T-test критерий, будет верно оценивать и строить доверительный интервал для истинного прироста. Доказательство корректности будет практически такое же, как и у T-test критерия из первой части. Дисперсия для такой функции также строится через дельта-метод, а формула практически полностью повторяет формулу для дисперсии в T-test.
Формула дисперсии:

Формула дисперсии в случае выборок разного размера

Код проверки корректности метода на A/B- и A/A-тестах
В этот раз код будет не таким простым. Но очень много кусков взято из реализации relative_ttest из первой части.
# 2. Создание тестируемого критерия.
def relative_cuped(control, test, control_before, test_before):
theta = (np.cov(control, control_before)[0, 1] + np.cov(test, test_before)[0, 1]) /\
(np.var(control_before) + np.var(test_before))
control_cup = control - theta * control_before
test_cup = test - theta * test_before
mean_den = np.mean(control)
mean_num = np.mean(test_cup) - np.mean(control_cup)
var_mean_den = np.var(control) / len(control)
var_mean_num = np.var(test_cup) / len(test_cup) + np.var(control_cup) / len(control_cup)
cov = -np.cov(control_cup, control)[0, 1] / len(control)
relative_mu = mean_num / mean_den
relative_var = var_mean_num / (mean_den ** 2) + var_mean_den * ((mean_num ** 2) / (mean_den ** 4))\
- 2 * (mean_num / (mean_den ** 3)) * cov
relative_distribution = sps.norm(loc=relative_mu, scale=np.sqrt(relative_var))
left_bound, right_bound = relative_distribution.ppf([0.025, 0.975])
ci_length = (right_bound - left_bound)
pvalue = 2 * min(relative_distribution.cdf(0), relative_distribution.sf(0))
effect = relative_mu
return ExperimentComparisonResults(pvalue, effect, ci_length, left_bound, right_bound)
# 3. Заводим счётчик.
bad_cnt = 0
# 4. Цикл проверки.
N = 30000
cis = []
for i in tqdm_notebook(range(N)):
# 4.a. Тестирую A/B-тест.
control_before = sps.expon(scale=1000).rvs(1000)
control = control_before + sps.norm(loc=0, scale=100).rvs(1000)
test_before = sps.expon(scale=1000).rvs(1000)
test = test_before + sps.norm(loc=0, scale=100).rvs(1000)
test *= 1.1
# 4.b. Запускаю критерий.
_, _, ci, left_bound, right_bound = relative_cuped(control, test, control_before, test_before)
cis.append(ci)
# 4.c. Проверяю, лежит ли истинная разница средних в доверительном интервале.
if left_bound > 0.1 or right_bound < 0.1:
bad_cnt += 1
# 5. Строю доверительный интервал для конверсии ошибок у критерия.
left_real_level, right_real_level = proportion_confint(count = bad_cnt, nobs = N, alpha=0.05, method='wilson')
# Результат.
print(f"Реальный уровень значимости: {round(bad_cnt / N, 4)};"
f" доверительный интервал: [{round(left_real_level, 4)}, {round(right_real_level, 4)}]")Реальный уровень значимости: 0.0506; доверительный интервал: [0.0481, 0.0531].
Результаты для A/A-тестов: реальный уровень значимости: 0.048; доверительный интервал: [0.046, 0.0503].
Отлично! Мы смогли построить относительный критерий для CUPED, который корректно работает.
Итого: если вы ещё не используете CUPED для A/B-тестов, самое время это исправить. Пишется не сложнее, чем T-test, но при этом сильно улучшает мощность критериев.

Теперь предлагаю поговорить про бутстрап-аналог CUPED–метода.
Постнормировка
Идея метода та же, что и в CUPED: использовать предэкспериментальный период. Ранее мы вычитали метрику, но ведь можно не только вычитать, но и делить:
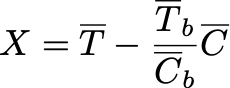
Утверждается, что математическое ожидание этой случайной величины совпадает с мат. ожиданием изначальной разницы теста и контроля. В чём логический смысл такой статистики? Допустим, мы случайно поделили выборку на тест и контроль, но сделали это плохо. К примеру, среднее в тесте на предпериоде в 2 раза больше, чем среднее в контроле. Тогда очень вероятно, что и без всякого тритмента среднее в тесте и в контроле будут отличаться друг от друга примерно в 2 раза. Поэтому, давайте домножим контроль на 2 и сбалансируем значения в группах на экспериментальном периоде.
То есть логика метода такая: уменьшим влияние шума, возникшего при делении на тест и контроль.
Теоретическое обоснование корректности

Осталось понять матожидание произведения. Заметим, что если выборки теста и контроля независимы, то есть следующее свойство:

А значит:
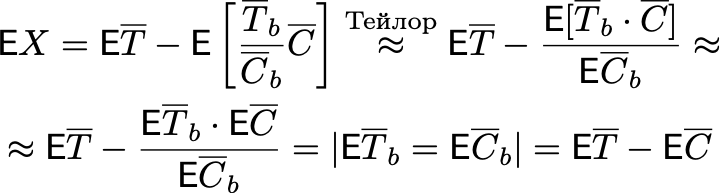
В относительной постановке статистика будет такой — идея та же, что и в абсолютной постановке:
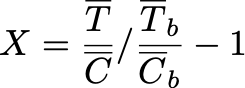
То есть мы смотрим, как раньше и сейчас тест относится к контролю. Если раньше тест был больше контроля в 2 раза, и сейчас мы получили такие же результаты, то наш тритмент никак не улучшил метрику.
Доказательство корректности
Для доказательства корректности этой формулы я не могу сослаться на ряд Тейлора. Можно было бы расписать через усиленный закон чисел, но для оригинальности посмотрим на доказательство по-другому.
По центральной предельной теореме все четыре выборки распределены нормально, а значит у нас есть отношение четырёх нормальных случайных величин. Так вот утверждается, что если знаменатель достаточно отдалён от 0, то отношение двух случайных величин, распределённых нормально, есть также случайная величина из нормального распределения. Поэтому в итоге статистика X будет распределена нормально с математическим ожиданием, которое мы хотим оценить в относительной постановке.
А теперь вопрос: как такое считать? Выписанная ранее формула дисперсии при делении двух случайных величин друг на друга уже внушает страх многим из нас, а тут у нас целых четыре отношения друг к другу! Здесь на помощь приходит один из лучших методов в статистике, который может помочь в любой непонятной ситуации, — bootstrap.
Бутстрап — это статистический метод, который позволяет по одной выборке построить «приблизительно» доверительный интервал для любой статистики, зависящей от выборки целиком.
Чуть подробнее о методе
К примеру, мы хотим построить доверительный интервал для отношения четырёх средних величин. У нас всего одна выборка (состоящая из четырёх частей: тест, контроль и они же на предпериоде), а значит, и одна статистика. Но по одному значению не построить распределение или доверительный интервал. Бутстрап позволяет решить эту проблему.
Для иллюстрации работы метода я предлагаю рассмотреть пример с покемонами. Пусть у нас есть изначальная выборка покемонов с некоторым значением статистики. Метод бутстрапа предлагает из одной этой выборки покемонов сделать бесконечно много выборок. Как? С помощью простого выбора элементов с повторением из изначальной выборки. Тогда у каждой новой выборки можно посчитать свою статистику, и по этим данным построить доверительный интервал. Единственное, о чем надо помнить: размер новых выборок должен быть таким же, как и у изначальной выборки. Подробнее узнать о методе можно на Википедии.
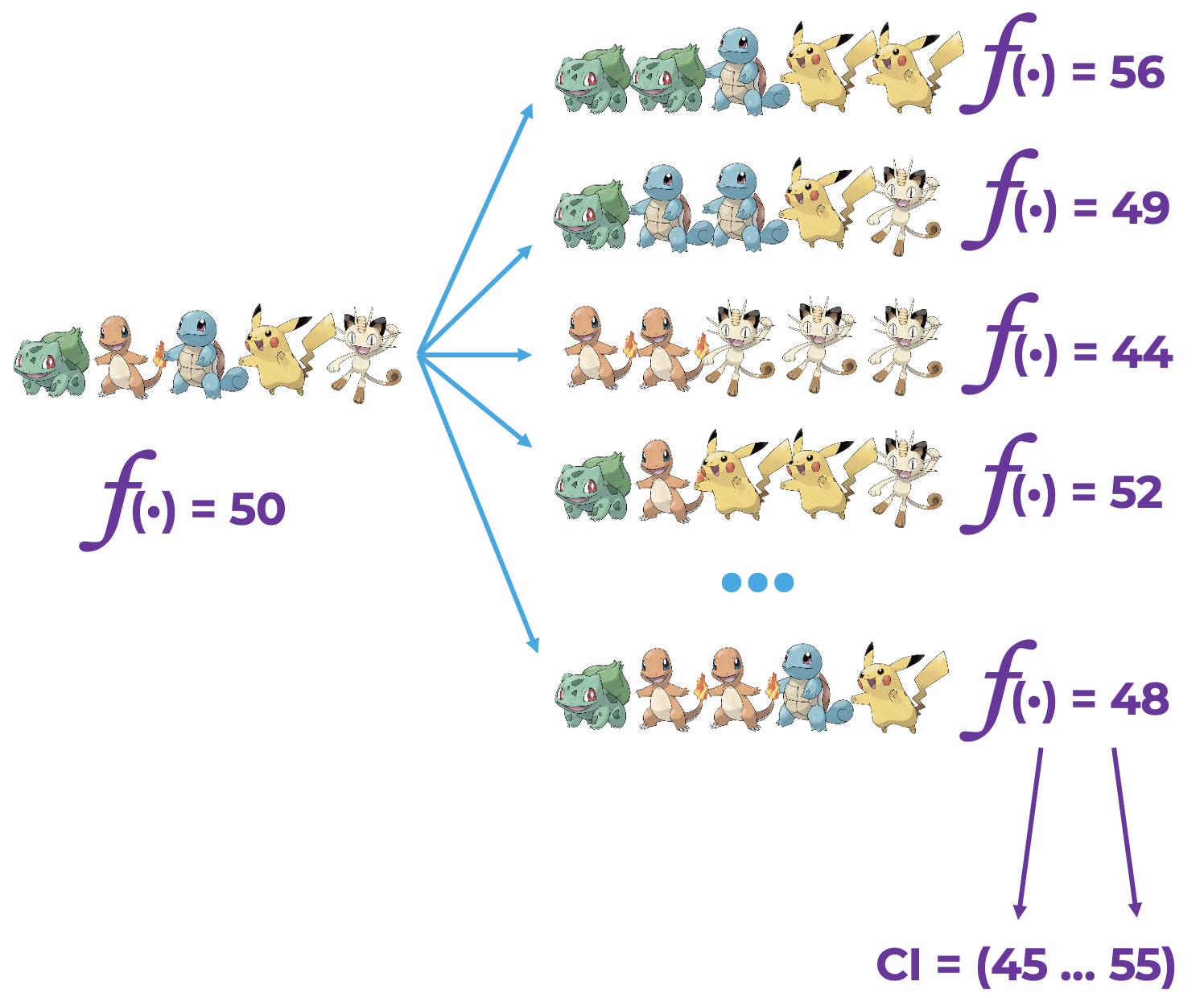
Благодаря тому, что бутстрап может построить доверительный интервал для любой статистики, статистический критерий практически не отличается в относительной и в абсолютных постановках. Единственное различие — это статистика, которую метод считает по выборке.
В случае абсолютной постановки A/B-теста:
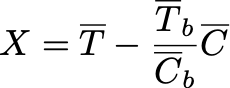
В относительной:
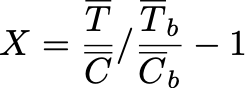
Если же реализовывать аналог T-test через бутстрап, то внутри критерия надо будет считать такие статистики:

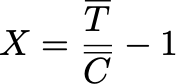
A/A- и A/B-проверка
Бутстрап-критерий. Код может казаться большим, но это обман. Смысловой части здесь мало, а всё, что меняется при переходе от абсолютной к относительной постановке, скрыто в первых двух строчках критерия.
def bootstrap(control, test, test_type='absolute'):
# Функция от средних, которую надо посчитать на каждой выборке.
absolute_func = lambda C, T: T - C
relative_func = lambda C, T: T / C - 1
boot_func = absolute_func if test_type == 'absolute' else relative_func
stat_sample = []
batch_sz = 100
# В теории boot_samples_size стоить брать не меньше размера выборки. Но на практике можно и меньше.
boot_samples_size = len(control)
for i in range(0, boot_samples_size, batch_sz):
N_c = len(control)
N_t = len(test)
# Выбираем N_c элементов с повторением из текущей выборки.
# И чтобы ускорить этот процесс, делаем это сразу batch_sz раз
# Вместо одной выборки мы получим batch_sz выборок
control_sample = np.random.choice(control, size=(len(control), batch_sz), replace=True)
test_sample = np.random.choice(test, size=(len(test), batch_sz), replace=True)
C = np.mean(control_sample, axis=0)
T = np.mean(test_sample, axis=0)
assert len(T) == batch_sz
# Добавляем в массив посчитанных ранее статистик batch_sz новых значений
# X в статье – это boot_func(control_sample_mean, test_sample_mean)
stat_sample += list(boot_func(C, T))
stat_sample = np.array(stat_sample)
# Считаем истинный эффект
effect = boot_func(np.mean(control), np.mean(test))
left_bound, right_bound = np.quantile(stat_sample, [0.025, 0.975])
ci_length = (right_bound - left_bound)
# P-value - процент статистик, которые лежат левее или правее 0.
pvalue = 2 * min(np.mean(stat_sample > 0), np.mean(stat_sample < 0))
return ExperimentComparisonResults(pvalue, effect, ci_length, left_bound, right_bound)A/B-тест: реальный уровень значимости: 0.0486; доверительный интервал: [0.0446, 0.053].
A/A-тест: реальный уровень значимости: 0.0541; доверительный интервал: [0.0498, 0.0587].
Постнормировка.
def post_normed_bootstrap(control, test, control_before, test_before, test_type='absolute'):
# Функция от средних, которую надо посчитать на каждой выборке.
absolute_func = lambda C, T, C_b, T_b: T - (T_b / C_b) * C
relative_func = lambda C, T, C_b, T_b: (T / C) / (T_b / C_b) - 1
boot_func = absolute_func if test_type == 'absolute' else relative_func
stat_sample = []
batch_sz = 100
#В теории boot_samples_size стоить брать не меньше размера выборки. Но на практике можно и меньше.
boot_samples_size = len(control)
for i in range(0, boot_samples_size, batch_sz):
N_c = len(control)
N_t = len(test)
# Надо помнить, что мы семплируем именно юзеров
# Поэтому, если мы взяли n раз i элемент в выборке control
# То надо столько же раз взять i элемент в выборке control_before
# Поэтому будем семплировать индексы
control_indices = np.arange(N_c)
test_indices = np.arange(N_t)
control_indices_sample = np.random.choice(control_indices, size=(len(control), batch_sz), replace=True)
test_indices_sample = np.random.choice(test_indices, size=(len(test), batch_sz), replace=True)
C = np.mean(control[control_indices_sample], axis=0)
T = np.mean(test[test_indices_sample], axis=0)
C_b = np.mean(control_before[control_indices_sample], axis=0)
T_b = np.mean(test_before[test_indices_sample], axis=0)
assert len(T) == batch_sz
stat_sample += list(boot_func(C, T, C_b, T_b))
stat_sample = np.array(stat_sample)
# считаем истинный эффект
effect = boot_func(np.mean(control), np.mean(test), np.mean(control_before), np.mean(test_before))
left_bound, right_bound = np.quantile(stat_sample, [0.025, 0.975])
ci_length = (right_bound - left_bound)
# P-value - процент статистик, которые лежат левее или правее 0.
pvalue = 2 * min(np.mean(stat_sample > 0), np.mean(stat_sample < 0))
return ExperimentComparisonResults(pvalue, effect, ci_length, left_bound, right_bound)A/B-тест: реальный уровень значимости: 0.0492; доверительный интервал: [0.0468, 0.0517].
Как я покажу далее, на реальных данных постнормировка работает не хуже, чем CUPED, но пишется проще: нет никаких страшных дисперсий и распределений.
Итого: главное, что надо запомнить о бустрап-критериях:
Не хотите думать — используйте бутстрап! Вся теория зашита в самом методе, дисперсию выводить математически не надо. Если есть интересующая статистика, бутстрап сразу для неё построит доверительный интервал. От вас в коде критерия надо поменять одну формулу подсчёта статистики по выборке.
Главный минус — такие критерии ну очень долгие. Конечно, есть хаки с распараллеливанием, пуассоновским бутстрапом и т. п. Но они всё ещё не ускорят его настолько, чтобы он был быстрее T-test подобных критериев.

Улучшенное разделение пользователей на тест и контроль
Мы посмотрели, как можно увеличивать мощность A/B–тестов, улучшая мощность критерия. Но кроме этого можно подумать о том, как лучше поделить пользователей на тест и контроль, чтобы:
тест и контроль были всё также сбалансированы;
дисперсия разницы теста с контролем стала бы сама по себе меньше.
Поэтому поговорим о стратификации.
Стратификация
Рассмотрим самый простой пример для визуализации: пусть у нас есть генеральная совокупность пользователей-покемонов:

Мы захотели провести на них A/B-тест. К примеру, раздать скидки на услуги Авито. При обычном A/B-тестировании мы случайно разбиваем всю выборку на тест и контроль, к примеру так:
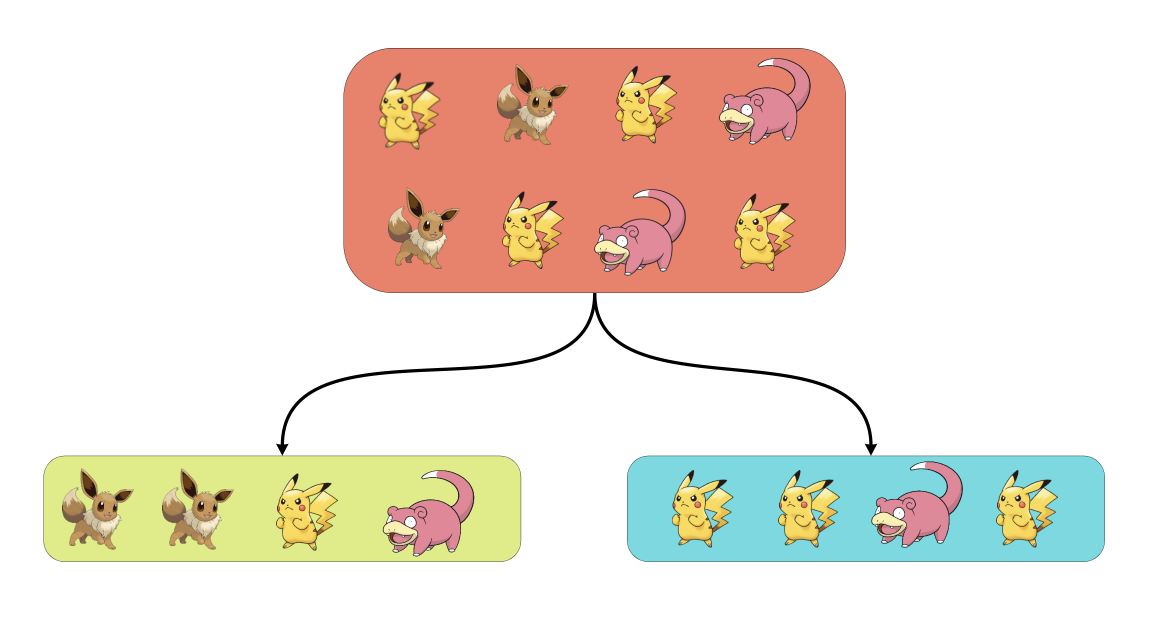
Дальше к этому мы применяем T-test, бутстрап, CUPED и т.д. и считаем результаты. Но вопрос: а что, если Пикачу (жёлтенькие) реагируют на тритмент не так, как Слоупоки (розовенькие)? Это вносит дополнительный шум в данные, так как в одной выборке три Пикачу, а в другой — один.
Поэтому давайте добавим вспомогательный шаг при делении выборки на тест и контроль. Сначала сгруппируем всех покемонов по виду, а потом будем сэмплировать из каждой группы (или страты) половину покемонов в тест, а другую — в контроль. Этот метод и называется стратификацией.
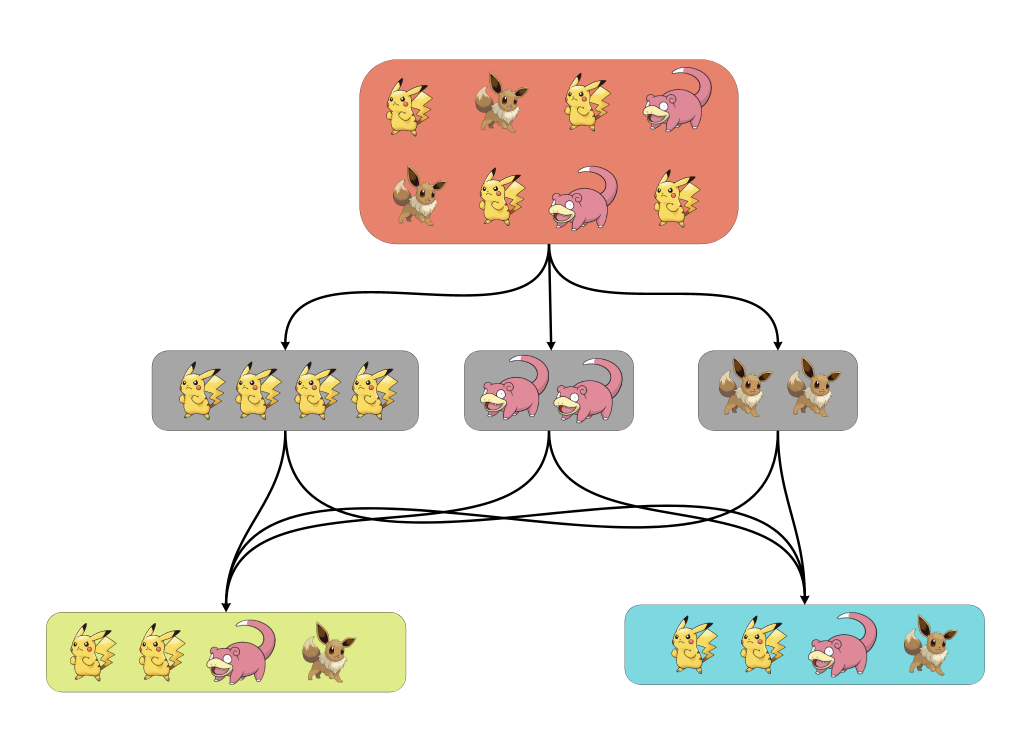
Утверждается, что дисперсия выборок при случайном делении и стратифицированном делении будет разной.
Формулы дисперсий

Где:
K — количество видов покемонов.
p_k — вероятность случайного покемона в изначальной выборке быть покемоном типа k.
σ_k — стандартное отклонение метрики в группе покемонов k.
μ_k — среднее метрики в группе покемонов k.
μ — среднее метрики на всей популяции покемонов.
Дисперсия стратифицированной выборки состоит из взвешенных дисперсий внутри страт. А дисперсия при случайном — обычном — разбиении состоит из дисперсии стратифицированной выборки и взвешенной «дисперсии между стратами». Таким образом, уменьшение вариации происходит за счёт выкидывания дисперсии между страт и оставление её лишь внутри групп.
На практике же примеры признаков, по которым можно группировать пользователей на страты, — это:
пол;
возраст;
страна/город проживания;
компания или частное лицо;
кластеризация с помощью машинного обучения;
всё, что придет нам в голову.
Существует и некоторое усовершенствование такого метода: парная стратификация.
Парная стратификация и переход к парному критерию
Для начала распишем по шагам предлагаемый метод:
Отсортируем всех пользователей на предэкспериментальном периоде.
Разобьём всех юзеров на группы — страты — из двух стоящих подряд человек.
Из каждой страты случайно одного пользователя отправим в контроль, а другого — в тест.
Иллюстрация метода:
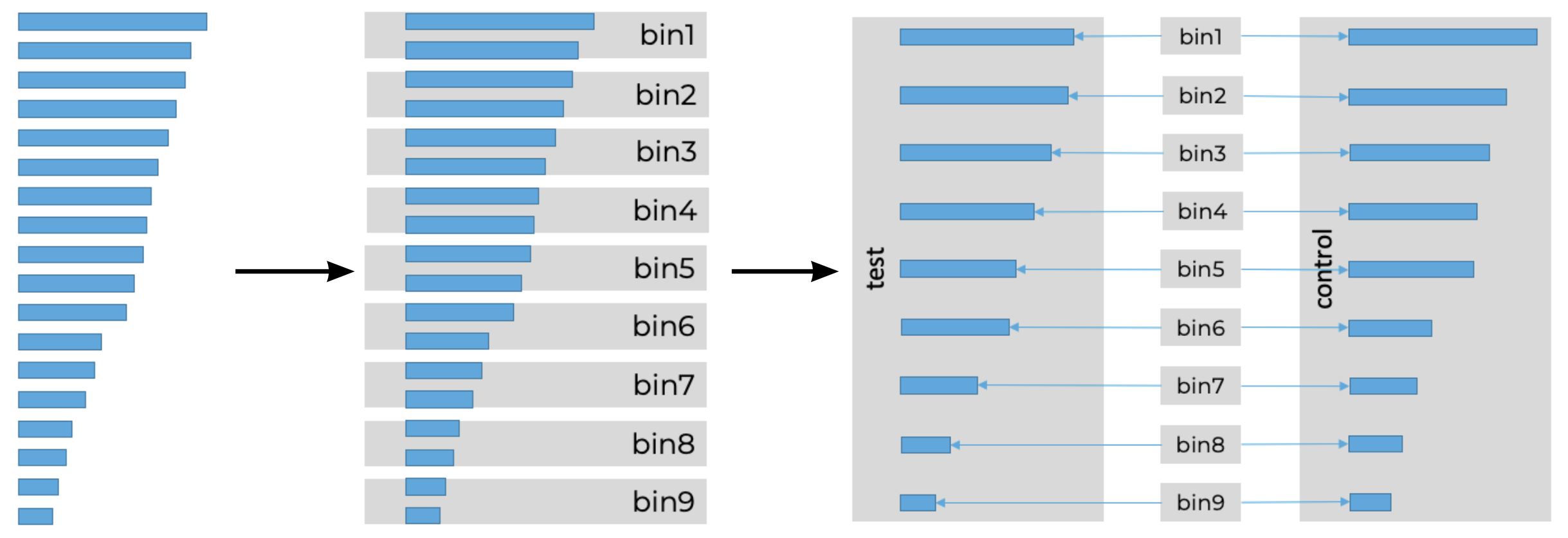
Как видно, идейно метод является продолжением идеи стратификации. Точно так же есть страты и точно так же половина группы уходит в контроль, а другая — в тест. Осталось лишь поменять критерий, держа в памяти, что дисперсия у стратифицированных выборок меньше, чем дисперсия при случайном разбиении. Но есть ещё беда: как я покажу далее, выборки теста и контроля станут зависимыми! Поэтому предлагается соединить две выборки T и C.
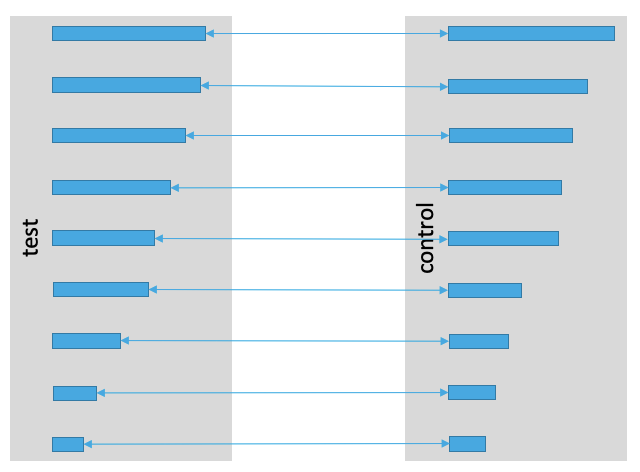
Как их соединить? Давайте перейдём к новой случайной величине Z=T-C. Для неё мы будем считать среднее и строить доверительный интервал. Поэтому от обычных критериев перейдём к спаренным.

Посмотрим на примерах, как в этом случае меняются критерии
Главное отличие в том, что в неспаренных критериях дисперсию можно считать по отдельности на тесте и контроле, а в спаренных надо учитывать ковариацию между ними. Казалось бы, откуда ковариация? Элементы выборки независимы между собой, а значит, тест с контролем должны быть независимы друг от друга. Но это не так.

Как видно, у обычного T-test поменяется только строчка с оценкой дисперсии: вместо суммы дисперсий теперь считается одна дисперсия разности, которая учитывает в себе ненулевую ковариацию T и C. Для относительного T-test надо реализовать ровно формулу дисперсии, учитывающую ковариацию. Я приводил её в первой статье.
Посмотрим на относительный CUPED:
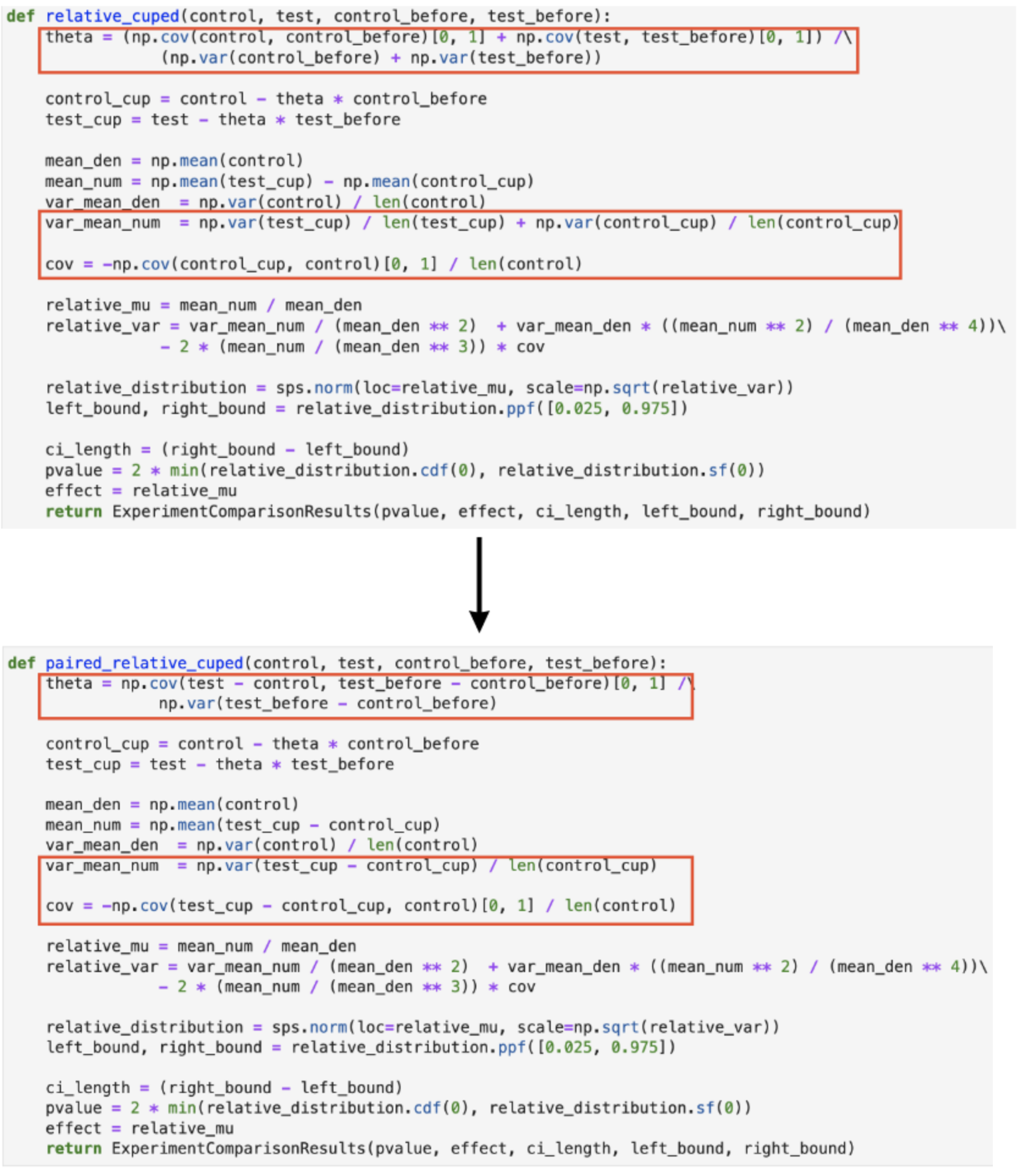
Здесь как раз вида разница в подсчёте θ, но оба варианта я расписал ранее.
Для бутстрапа изменения немного другие: теперь надо сэмплировать бутстрапные выборки T и С не по отдельности, а вместе:
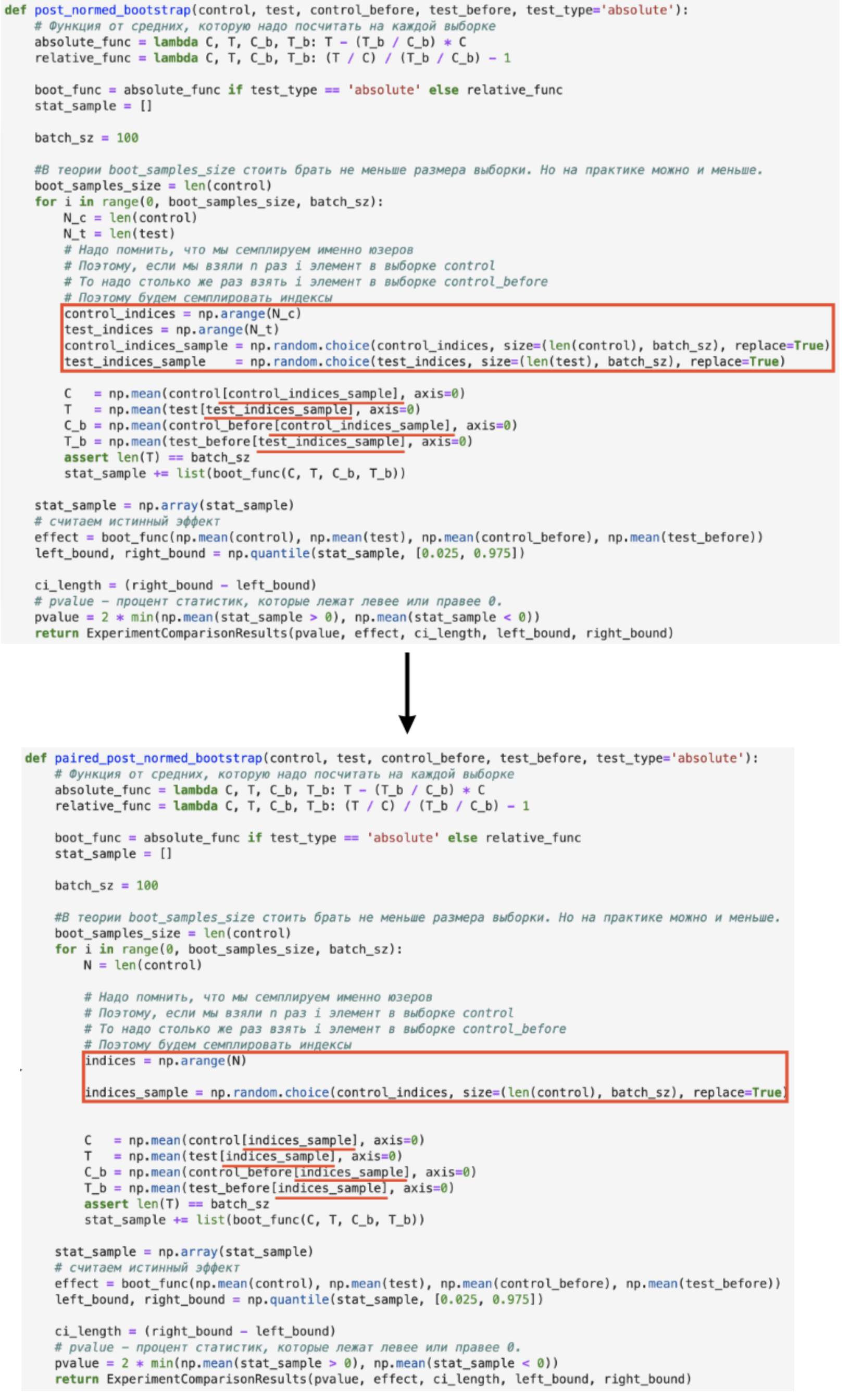
Теперь я предлагаю на примере посмотреть, как этот метод работает для T-test, а ещё на сравнение результатов спаренного и обычного критериев.
Сравнение спаренных и обычных критериев
def splitter(before_metrics):
size = len(before_metrics)
# отсортируем массив
sorted_array = np.sort(before_metrics)[::-1]
control = []
test = []
for i in range(0, size, 2):
if np.random.rand() < 0.5:
control.append(sorted_array[i])
test.append(sorted_array[i + 1])
else:
control.append(sorted_array[i + 1])
test.append(sorted_array[i])
return np.array(control), np.array(test)
bad_cnt_paired = 0
paired_power = 0
bad_cnt = 0
power = 0
N = 30000
for i in tqdm_notebook(range(N)):
before = sps.expon(scale=1000).rvs(4000)
C_b, T_b = splitter(before)
C = C_b + sps.norm(loc=0, scale=100).rvs(2000)
T = T_b + sps.norm(loc=0, scale=100).rvs(2000)
T *= 1.01
_, _, _, left_bound, right_bound = relative_ttest(C, T)
_, _, _, left_bound_paired, right_bound_paired = paired_relative_ttest(C, T)
if left_bound > 0.01 or right_bound < 0.01:
bad_cnt += 1
if left_bound_paired > 0.01 or right_bound_paired < 0.01:
bad_cnt_paired += 1
if left_bound > 0:
power += 1
if left_bound_paired > 0:
paired_power += 1
left_real_level, right_real_level = proportion_confint(count = bad_cnt, nobs = N,
alpha=0.05, method='wilson')
left_real_level_paired, right_real_level_paired = proportion_confint(count = bad_cnt_paired, nobs = N,
alpha=0.05, method='wilson')
print(f"Реальный уровень значимости для обычного критрия: {round(bad_cnt / N, 4)};"\
f" доверительный интервал: [{round(left_real_level, 5)}, {round(right_real_level, 5)}]")
print(f"Реальный уровень значимости для спаренного критерия: {round(bad_cnt_paired / N, 4)};"\
f" доверительный интервал: [{round(left_real_level_paired, 5)}, {round(right_real_level_paired, 5)}]")
print(f"Мощность спаренного критерия vs. мощность обычного критерия: {paired_power / N} VS. {power / N}")Реальный уровень значимости для обычного критерия: 0.0; доверительный интервал: [0.0, 0.00013].
Реальный уровень значимости для спаренного критерия: 0.0513; доверительный интервал: [0.04886, 0.05385].
Мощность спаренного критерия vs. мощность обычного критерия: 0.8623 vs. 0.0.
Обычный критерий «заширяет» доверительный интервал: во всех случаях истинный прирост попал в доверительный интервал, хотя в 5% не должен был. Чем это плохо? Обычный критерий строит слишком большой доверительный интервал для прироста, и 0 всё время будет лежать в этом интервале. Такой критерий не подходит в случае, когда мы боремся за мощность метода. Это видно и на результатах сравнения мощности: парный критерий имеет мощность 86%, обычный — 0%.
В случае, если выборки не спарены:
Реальный уровень значимости для обычного критерия: 0.0503; доверительный интервал: [0.04792, 0.05287].
Реальный уровень значимости для спаренного критерия: 0.0519; доверительный интервал: [0.04939, 0.05446].
Мощность спаренного критерия vs. мощность обычного критерия: 0.056 vs. 0.044.
Видно, что в случае спаренных выборок результаты сильно лучше: вместо мощности в 5% мы получили 86%. А ещё спаренный критерий корректно отработал как при парно стратифицированных выборках, так и при обычном делении.
В чём прелесть спаренных критериев: они работают и в неспаренных случаях, когда не была применена парная стратификация. Они просто дополнительно учитывают ковариацию между выборками, которой нет в случае обычных выборок. По идее, спаренные критерии могут добавить шума в доверительный интервал, но наши реальные и искусственные эксперименты показывают, что этого или не происходит, или шум незаметен в сравнении с шумом в самих выборках.
Поэтому, используя парные критерии, вы не ухудшите результаты A/B-тестов. Но в случае парной стратификации сможете улучшить их мощность.
Для тех, кто заинтересовался методом и не боится небольшого количества математики, предлагаю обсудить теорию, стоящую за ним.
Теория
Рассмотрим сначала на тех же искусственных примерах, что и ранее, ковариацию между T и C:
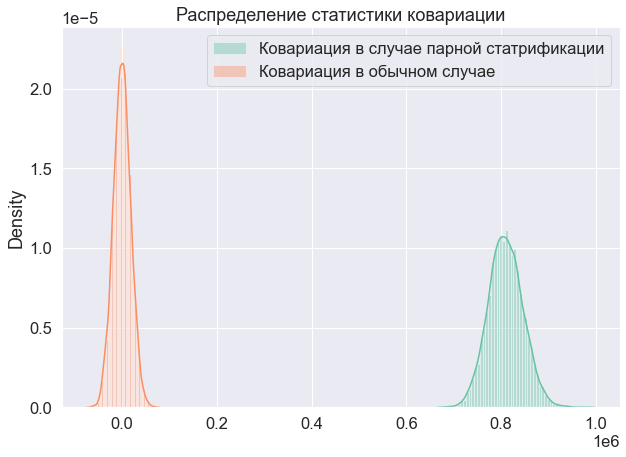
Ковариация в случае парной стратификации не нулевая, а значит, выборки не независимы. Теперь докажем это через теоретические выкладки.
Для начала покажем, почему вообще спаренные критерии уменьшают здесь дисперсию. Для этого докажем существование ковариации между T и C в случае парной стратификации. Распишем наши текущие метрики через их значения на предпериоде, по которому мы сортируем, и через некоторую случайную величину ε, который появляется при переходе к экспериментальному периоду.
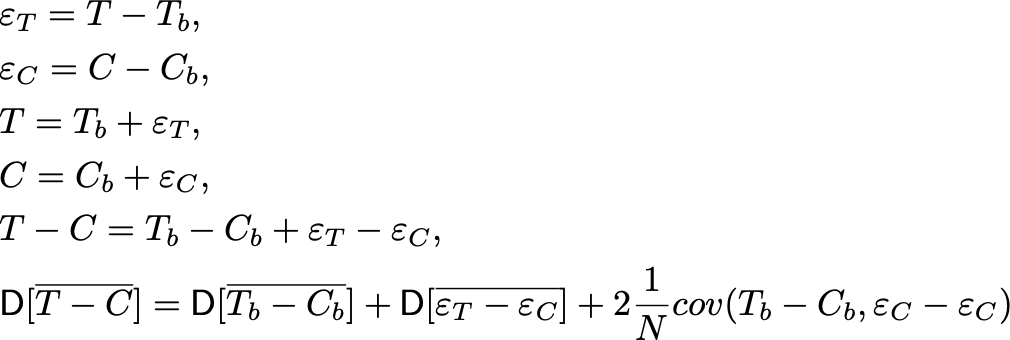
Распишем дисперсию на предпериоде. Она равна:
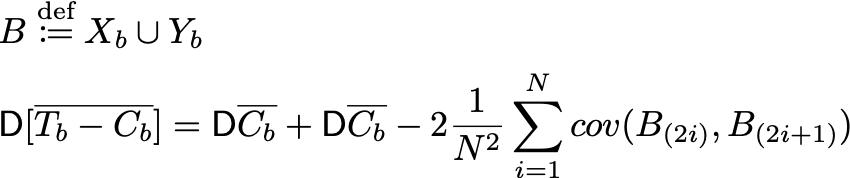
Доказательство:
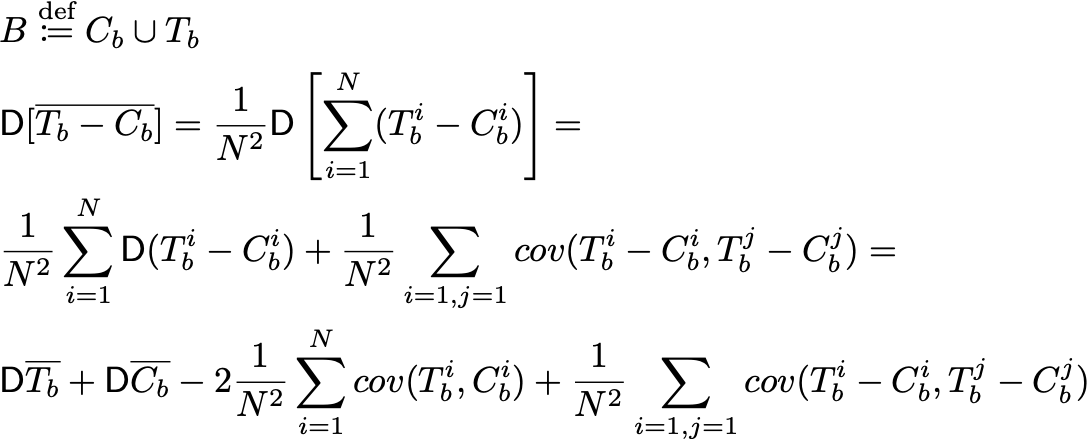
Теперь вспомним, что T_b^i, C_b^i — это i-ые порядковые статистики в этих выборках. А в объединённой выборке B — это две подряд стоящих порядковых статистики B_(2i-1), B_(2i). Но мы не знаем, B_(2i) = T_b^i или B_(2i)=C_b^i. Зато знаем, что вероятность каждого из этих двух вариантов равна 1/2. Тогда ковариации расписываются так:
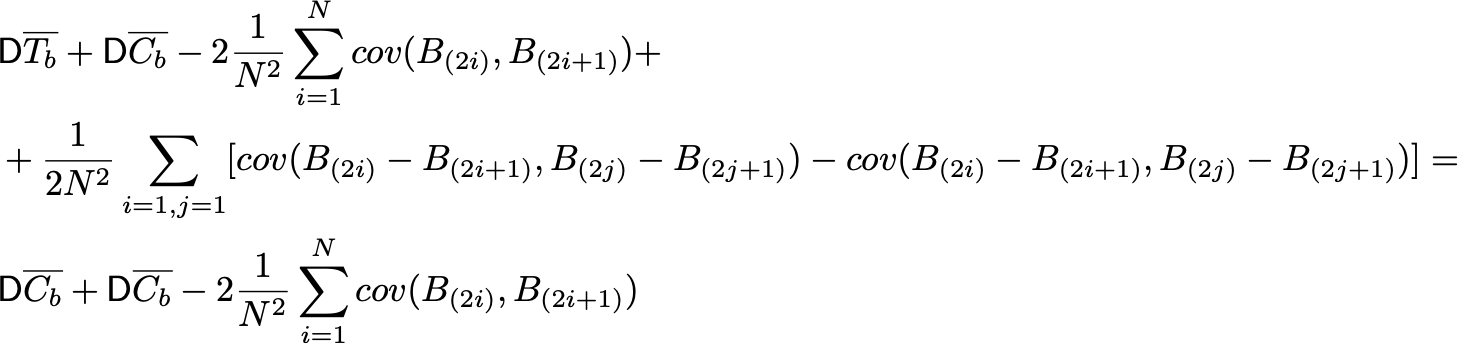
Ковариация между двумя порядковыми статистиками будет положительной. К примеру, для равномерного распределения значения ковариации можно посчитать теоретически. Отсюда же получается, что существует положительная ковариация между выборками теста и контроля на предэкспериментальном периоде. Хотя казалось бы, все элементы выборок независимы между собой. То есть у парно стратифицированных выборок на предпериоде дисперсия будет меньше, чем у обычных. ч.т.д.
Теперь рассмотрим оставшиеся слагаемые, образующие дисперсию разницы D[T-C]. Для простоты посчитаем, что ε не зависит от предпериода. Тогда:

Причём этот переход не зависит от рассматриваемого метода: если бы стратификации не было, но переход остался точно таким же. Поэтому парная стратификация уменьшила дисперсию только благодаря добавлению положительной ковариации на предпериоде. Отсюда также следует, что:
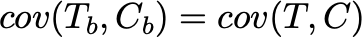
Итого, на экспериментальном периоде у нас также есть зависимость теста и контроля. Поэтому дисперсия станет меньше.
Теперь посмотрим на случай, когда ε зависит от предпериода:

Может ли быть такое, что на предпериоде ковариация была положительной, как мы показали ранее, а на экспериментальном периоде — отрицательной? Вообще, да, если предположить, что наш тритмент так повлиял на выборку, что чем больше ранее было значение метрики, тем меньше оно будет сейчас. Те, кто раньше платил меньше всего, сейчас начнут платить больше всех. В таком случае дисперсия может стать больше.
Например, пусть у нас на экспериментальном периоде тритмент просто зеркально отразил метрику на предпериоде, а в контроле она осталась такой же. Тогда посмотрим на ширину доверительных интервалов в случае использования парного и обычного критерия:
ci_NOT_splitted_length = []
ci_splitted_length = []
N = 1000
# сплитование
for i in tqdm_notebook(range(N)):
before = sps.expon(scale=1000).rvs(4000)
# уже отсортированы
C_b, T_b = splitter(before)
C = C_b
T = -1 * T_b
_, _, ci_splitted_sample, _, _ = paired_ttest(C, T)
ci_splitted_length.append(ci_splitted_sample)
###################################
# не было сплитования
for i in tqdm_notebook(range(N)):
before = sps.expon(scale=1000).rvs(4000)
C_b, T_b = before[:2000], before[2000:]
C = C_b
T = -1 * T_b
_, _, ci_NOT_splitted_sample, _, _ = absolute_ttest(C, T)
ci_NOT_splitted_length.append(ci_NOT_splitted_sample)
print("ширина доверительного интервала в случае неспаренного критерия vs. спаренного критерия:"\
f" {round(np.mean(ci_NOT_splitted_length), 2)} VS. {round(np.mean(ci_splitted_length), 2)}")
print(f"p-value сравнения: {absolute_ttest(np.array(ci_NOT_splitted_length), np.array(ci_splitted_length)).pvalue}")Ширина доверительного интервала в случае неспаренного критерия vs. спаренного критерия: 123.8 vs. 174.96. P-value сравнения: 0.0.
Так что да, возможно, что парная стратификация приведёт к заширению доверительного интервала. Но для этого надо, чтобы тритмент «перевернул» ваших юзеров (была большая метрика — стала маленькой и наоборот), что практически невозможно на практике.
Итого: парная стратификация — достаточно интересный метод уменьшения вариации с помощью добавления зависимости между тестом и контролем. И на практике он часто бывает хорош.
Сравнение всех методов
Время сравнить все рассмотренные ранее методы. До этого я доказывал корректность методов, но не показывал на практике, к чему приводят те или иные хаки. Пора это исправлять.
Для начала предлагаю определиться с метрикой, по которой стоит сравнивать критерии. Первая метрика, которая приходит в голову знакомым со статистикой, — это мощность. Так как я буду в A/B-симуляциях тестировать односторонние альтернативы, что среднее в тесте больше, чем в контроле, то и мощность нас интересует левосторонняя. То есть процент случаев, когда левая граница доверительного интервала больше 0. Но мощность не всегда показательна при различии двух методов.
К примеру, если есть огромный эффект, то любой критерий отвергнет гипотезу о равенстве средних, но при этом один даст широкий доверительный интервал, а другой — узкий. В таком случае, конечно, лучше будет использовать критерий с узким доверительным интервалом. Кроме того, нам нужно удостовериться в корректности методов. Поэтому ещё нам нужен реальный уровень значимости.
Итого, основные метрики, которые я буду использовать:
Реальный уровень значимости или ошибка первого рода, которая должна быть 5%.
Левосторонняя мощность.
Ширина доверительного интервала.
Дополнительная метрика
Так как я тестирую одностороннюю альтернативу, теория предполагает, что доверительный интервал будет иметь вид [L,∞). Поэтому, на самом деле нас интересует не ширина доверительного интервала, а расстояние от 0 до левой границы L. Чем больше это расстояние, тем будет лучше. Для примера посмотрим на иллюстрацию:
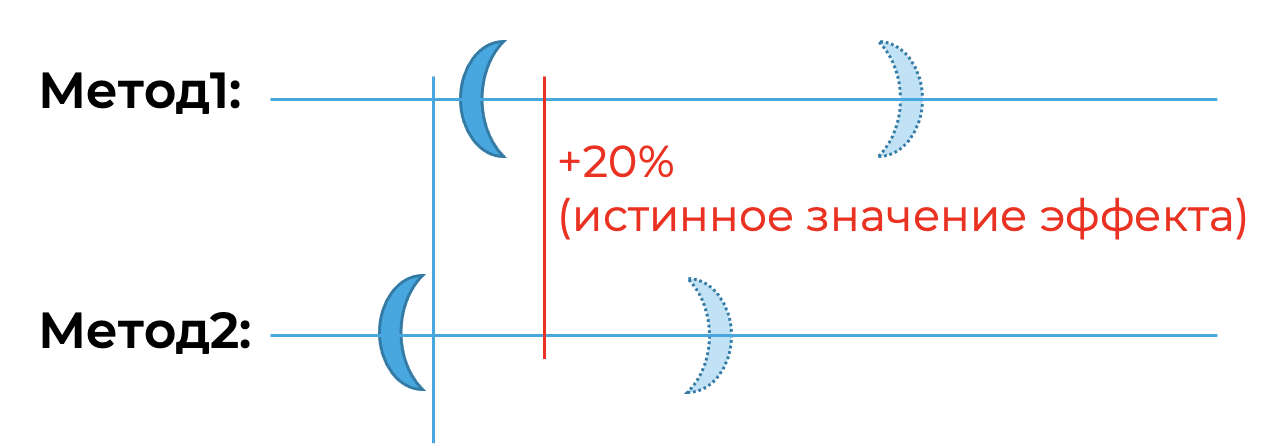
В методе один доверительный интервал (в случае двусторонней альтернативы) шире, но при этом он верно отвергает гипотезу о равенстве средних. А во втором методе наоборот: доверительный интервал уже, но при этом он не отвергнет равенство средних. Какой критерий на практике полезней? Конечно же первый.
Отсюда предлагается следующая метрика: расстояние левой границы до 0, которую надо максимизировать. Её можно переформулировать: расстояние левой границы до истинного эффекта, которую, наоборот, надо минимизировать.
Критерии, которые я буду сравнивать:
T-test.
Парный T-test.
CUPED.
Парный CUPED.
Парный CUPED без юзеров, отвечавших за 5% выручки на предэкспериментальном периоде. Это интерпретация метода борьбы с выбросами из первой части статьи.
Bootstrap.
Парный bootstrap.
Постнормировка.
Парная постнормировка.
Все эти методы оценены на 1000 датасетов, собранных на наших реальных данных по методу, описанном в первой части. Метрика, которую я смотрел, — выручка. В итоге я провёл статистические тесты в относительной/абсолютной постановке, на A/A-, A/B-тестах, в случае парно стратифицированных и обычных выборок. Но ввиду бесполезности А/А-тестов (ведь есть A/B-тесты, а А/А нужны только для проверки корректности), продемонстрирую только A/B-тесты.
Результаты получились такими:
Относительная постановка. Посмотрим на результаты на обычных, не стратифицированных выборках:

Цветовая легенда:
Синий цвет в реальном уровне значимости — статистический критерий статистически значимо ошибается меньше, чем заявленные 5%.
Зелёный цвет в реальном уровне значимости — процент ошибок у статистического критерия не статистически значимо отличается от 5%. А значит, критерий работает как заявлено.
Жирный шрифт в метриках — наилучший результат.
Была применена парная стратификация к выборкам:

Отсюда получились следующие результаты:
В случае нестратифицированных выборок парные и непарные критерии работают одинаково. Так что вы всегда можете безболезненно перейти на спаренные критерии при выборках одинакового размера.
CUPED по сравнению с T-test сокращает доверительный интервал в полтора раза (в случае нестратифицированных выборок) и увеличивает мощность на 13% (при небольшом эффекте). Если вы хотите начать получать больше статистически значимых результатов, то в первую очередь реализовывайте CUPED. Благо на SQL он также просто пишется. Не если вы по каким-то причинам не хотите его использовать, то можете реализовать постнормировку c примерно с такими же результатами.
Парная стратификация позволяет сократить доверительный интервал для CUPED примерно на 7% и увеличить мощность на 5%. При этом критерии, которые не учитывают её, совершают меньше ошибок, чем 5%, заширяя доверительный интервал, что и следовало из теории.
Если вы можете избавиться от топ-юзеров в A/B-тесте, не потеряв при этом репрезентативность, то качество для спаренного CUPED можно улучшить ещё на 3.5%.
Если бы мы использовали обычный T-test, то ширина доверительного интервала была бы 0.14, а мощность всего 16.6%. Но после использования всех лайфхаков из статьи мы смогли сократить его в 1.66 раза, а мощность поднять на 22%. Хочется отметить, что метрика выручки у нас самая шумная, поэтому достичь для неё таких результатов — это успех.
В абсолютной постановке получились такие же результаты, поэтому их я не привожу.
Итог
Я рассказал самое основное, что поможет сильно улучшить ваши текущие и будущие A/B-тесты. Перечислю ещё раз, что стоит запомнить из этой статьи:
Бывает бесполезно держать эксперимент слишком долго. Вы просто зря теряете время. Кроме того, чем дольше вы держите один A/B-тест, тем меньше гипотез успеваете проверить за определённый срок.
Вы не используете CUPED? Пора это исправить.
Если у вас есть очень страшная статистика, математическое ожидание которой вы хотите оценить на A/B-тесте, то на помощь может прийти бутстрап.
Любой используемый статистический критерий можно улучшить, если вы заранее стратифицируете выборку. Или воспользуетесь алгоритмом парной стратификации, который дополнительно добавит зависимость между тестом и контролем.
Если у вас остались вопросы, можете писать их мне в соц сетях:
тг: @dimon2016
