Всем привет! Меня зовут Дима Лунин, я аналитик в компании Авито. В этой статье я расскажу про критерий Манна-Уитни и проблемы при его использовании.
Этот критерий очень популярен. Во многих компаниях и на обучающих курсах рассказывают про два его важных преимущества:
Манн-Уитни — непараметрический собрат T-test. Если данные в A/B-тесте не из нормального распределения, то T-test использовать нельзя. На помощь приходит Манн-Уитни.
Манн-Уитни — робастный критерий. В данных часто бывает много шумов и выбросов, поэтому T-test неприменим по соображениям мощности, чувствительности или ненормальности данных. А Манн-Уитни в этот момент отлично срабатывает и более вероятно находит статистически значимый эффект.
Если вы анализировали A/B-тест, где вас интересовал прирост или падение какой-то метрики, то наверняка использовали критерий Манна-Уитни. Я хочу рассказать про подводные камни этого критерия, и почему мы в компании его не используем. А в конце вы поймёте, откуда взялся такой холиварный заголовок :)
План статьи такой:
Я теоретически покажу, что проверяет Манн-Уитни и почему это не имеет ничего общего с ростом медиан и среднего значения. А ещё развею миф, что Манн-Уитни проверяет эту гипотезу:
На примере искусственных и реальных данных продемонстрирую, что Манн-Уитни работает не так, как вы ожидаете. Его «преимущество» в большем числе прокрасов относительно T-test, и это — главный минус этого критерия, поскольку прокрасы ложные.
Расскажу про логарифмирование метрики и продемонстрирую, почему это плохая идея.
Покажу теоретические случаи, когда Манн-Уитни применим и его можно использовать для сравнения средних.
Отвечу на вопрос: как тогда жить и какой критерий использовать для анализа A/B-тестов.
Что проверяет критерий Манна-Уитни?
Предлагаю ответить на вопрос: можем ли мы проверять равенство средних или медиан в тесте и в контроле с помощью критерия Манна-Уитни? Или проверять, что одна выборка «не сдвинута» относительно другой выборки? Или, если на языке математики:
Например, у нас в A/B-тесте две выборки:
U[−1, 1] — равномерное распределение от −1 до 1
U[−100, 100] — равномерное распределение от −100 до 100
Про эти два распределения мы знаем, что у них равны средние и медианы, и что они симметричны относительно 0. Кроме того, вероятность, что сгенерированное значение в первой выборке будет больше значения во второй выборке, равна 1/2. Или, если сформулировать математически, P(T > C) = 1/2, где T и C — выборки теста и контроля.
Я хочу проверить, работает ли здесь корректно Манн-Уитни. Для этого запустим эксперимент 1000 раз и посмотрим на количество отвержений нулевой гипотезы у критерия. Подробнее про этот метод можно прочесть в моей статье про улучшение A/B тестов. Если бы критерий Манна-Уитни работал как надо и проверял одну из гипотез, то по определению уровня значимости он бы ошибался на этих тестах в 5% случаев, с некоторым разбросом из-за шума.
Проверим корректность примера на уровне значимости для T-test критерия:
# Подключим библиотеки
import scipy.stats as sps
from tqdm.notebook import tqdm # tqdm – библиотека для визуализации прогресса в цикле
from statsmodels.stats.proportion import proportion_confint
import numpy as np
# Заводим счетчики количества отвергнутых гипотез для Манна-Уитни и для t-test
mann_bad_cnt = 0
ttest_bad_cnt = 0
# Прогоняем критерии 1000 раз
sz = 1000
for i in tqdm(range(sz)):
# Генерируем распределение
test = sps.uniform(loc=-1, scale=2).rvs(1000) # U[-1, 1]
control = sps.uniform(loc=-100, scale=200).rvs(1000) # U[-100, 100]
# Считаем pvalue
mann_pvalue = sps.mannwhitneyu(control, test, alternative='two-sided').pvalue
ttest_pvalue = sps.ttest_ind(control, test, alternative='two-sided').pvalue
# отвергаем критерий на уровне 5%
if mann_pvalue < 0.05:
mann_bad_cnt += 1
if ttest_pvalue < 0.05:
ttest_bad_cnt += 1
# Строим доверительный интервал для уровня значимости критерия (или для FPR критерия)
left_mann_level, right_mann_level = proportion_confint(count = mann_bad_cnt, nobs = sz, alpha=0.05, method='wilson')
left_ttest_level, right_ttest_level = proportion_confint(count = ttest_bad_cnt, nobs = sz, alpha=0.05, method='wilson')
# Выводим результаты
print(f"Mann-whitneyu significance level: {round(mann_bad_cnt / sz, 4)}, [{round(left_mann_level, 4)}, {round(right_mann_level, 4)}]")
print(f"T-test significance level: {round(ttest_bad_cnt / sz, 4)}, [{round(left_ttest_level, 4)}, {round(right_ttest_level, 4)}]")Результат:
Mann-whitneyu significance level: 0.114, [0.0958, 0.1352]
T-test significance level: 0.041, [0.0304, 0.0551]T-test здесь корректно работает: он ошибается в 5% случаев, как и заявлено. А значит, пример валиден.
Манн-Уитни ошибается в 11% случаев. Если бы он проверял равенство средних, медиан или P(T > C) = 1/2, то должен был ошибиться только в 5%, как T-test. Но процент ошибок оказался в два раза больше. А значит, что эти гипотезы неверны для Манна-Уитни:
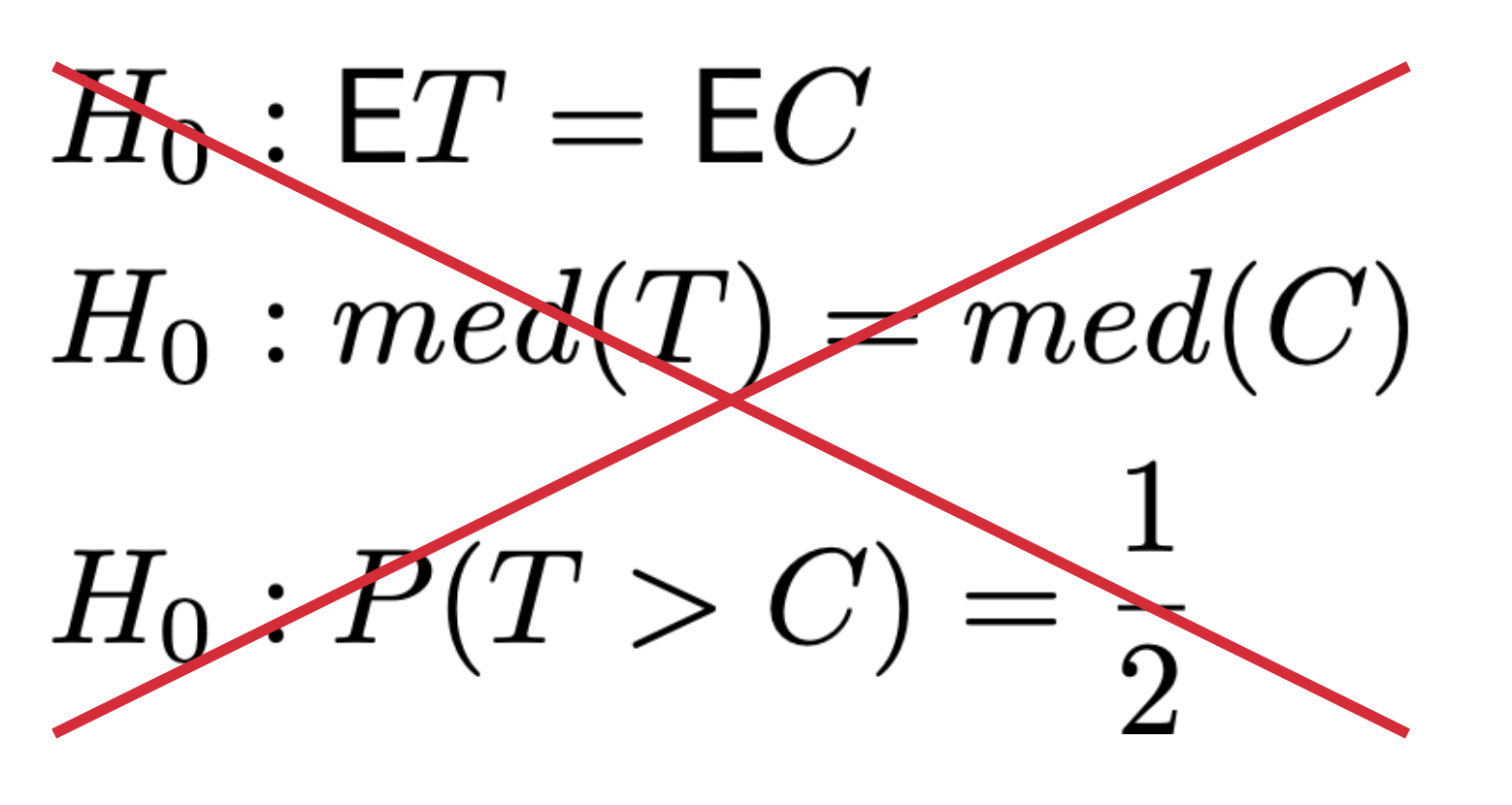
Этот метод можно использовать для проверки только такой гипотезы:
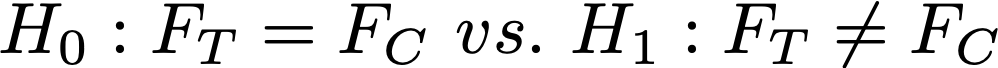
Этот критерий проверяет, что выборки теста и контроля взяты из одного распределения. Если он считает, что выборки из разных распределений — отвергает гипотезу. Это обычный критерий однородности.
Для демонстрации корректности я предлагаю снова запустить 1000 раз тесты, но выборки теста и контроля в этот раз взяты из одного распределения: U[-100, 100] (равномерное распределение от -100 до 100).
Проверка
# Подключим библиотеки
import scipy.stats as sps
from tqdm.notebook import tqdm # tqdm – библиотека для визуализации прогресса в цикле
from statsmodels.stats.proportion import proportion_confint
import numpy as np
# Заводим счетчики количества отвергнутых гипотез для Манна-Уитни и для t-test
mann_bad_cnt = 0
ttest_bad_cnt = 0
# Прогоняем критерии 1000 раз
sz = 1000
for i in tqdm(range(sz)):
# Генерируем распределение
test = sps.uniform(loc=-100, scale=200).rvs(1000) # U[-100, 100]
control = sps.uniform(loc=-100, scale=200).rvs(1000) # U[-100, 100]
# Считаем pvalue
mann_pvalue = sps.mannwhitneyu(control, test, alternative='two-sided').pvalue
ttest_pvalue = sps.ttest_ind(control, test, alternative='two-sided').pvalue
# отвергаем критерий на уровне 5%
if mann_pvalue < 0.05:
mann_bad_cnt += 1
if ttest_pvalue < 0.05:
ttest_bad_cnt += 1
# Строим доверительный интервал для уровня значимости критерия (или для FPR критерия)
left_mann_level, right_mann_level = proportion_confint(count = mann_bad_cnt, nobs = sz, alpha=0.05, method='wilson')
left_ttest_level, right_ttest_level = proportion_confint(count = ttest_bad_cnt, nobs = sz, alpha=0.05, method='wilson')
# Выводим результаты
print(f"Mann-whitneyu significance level: {round(mann_bad_cnt / sz, 4)}, [{round(left_mann_level, 4)}, {round(right_mann_level, 4)}]")
print(f"T-test significance level: {round(ttest_bad_cnt / sz, 4)}, [{round(left_ttest_level, 4)}, {round(right_ttest_level, 4)}]")
Результаты:
Mann-whitneyu significance level: 0.045, [0.0338, 0.0597]
T-test significance level: 0.043, [0.0321, 0.0574]Манн-Уитни не может проверить ничего, кроме равенства распределений. Этот критерий не подходит для сравнения средних или медиан.
Разберёмся, почему Манна-Уитни нельзя применять для сравнения средних, медиан и P(T > C) = 1/2. Для начала посмотрим на статистику, которая считается внутри критерия:

Для неё считаются те критические области, при попадании в которые статистики U критерий отвергнется.
Отсюда видно, что:
Манн-Уитни учитывает расположение элементов выборок относительно друг друга, а не значения элементов. Поэтому он не может сравнивать математические ожидания, если он даже не знает абсолютные значения элементов выборки.
Гипотеза H_0: P(T > C) = 1/2 неверна для данного критерия. Если P(T > C) = 1/2, то мат. ожидание EU = (произведение размера выборок) / 2. Но при равенстве распределений мат ожидание статистики U будет точно таким же. Почему критерий не сработал на примере с 2 разными равномерными распределениями U[-1, 1] VS U[-100, 100], но сработал при сравнении распределений U[-100, 100] VS U[-100, 100]? Суть в том, что мы не знаем распределение статистики U. Когда тест и контроль из одного распределения, мы знаем, что статистика U распределена нормально. Но если это не так, то теорема перестаёт работать. Тогда мы не знаем, как распределена статистика U, и не можем посчитать p-value.
По этой же причине критерий не может проверять равенство медиан.
Мы рассмотрели, почему Манна-Уитни не следует применять для проверки равенства средних, медиан и смещённости распределений. Но на практике его все равно часто применяют для этих гипотез, особенно для равенства средних. Что плохого может случиться в этом случае? Правда ли, что в таком случае мы завысим ошибку 1 рода в 2 раза и будем ошибаться в 11% вместо 5%?
Манн-Уитни при анализе реальных A/B-тестов: подводные камни
На реальных задачах проблемы Манна-Уитни будут куда серьёзнее, чем завышение alpha в два раза. Все последующие примеры будут основаны на кейсах, которые встречаются на практике в Авито. Я продемонстрирую работу критерия Манна-Уитни на искусственно сгенерированных данных, моделирующих один из наших экспериментов, а потом продемонстрирую результаты на настоящих данных из Авито.
Допустим, мы проводим A/B-тест с целью улучшить какую-то метрику. Тогда наше изменение чаще всего приводит к двум ситуациям:
Части пользователей понравилось наше воздействие и нулей в выборке стало меньше. Например, мы дали скидки на услуги, платящих пользователей стало больше.
Другой части пользователей не понравилось наше изменение и они оттекли по метрике — стало больше нулей.
В обоих этих случаях я покажу, как может работать критерий.
Кейс 1: прирост количества пользователей
Я разберу этот кейс на примере выдачи скидки. Количество платящих пользователей увеличилось, но ARPPU упал. Наша ключевая метрика — выручка. Мы хотим понять: начнём ли мы больше зарабатывать со скидками. Или выросло ли ARPU, математическое ожидание выручки — что эквивалентно.
Сразу зафиксируем проверяемую гипотезу о равенстве средних: H0 — средний чек не изменился или упал vs. H1 — средний чек вырос. Мы уже знаем, что Манн-Уитни может ошибаться в этой задаче. Но насколько?
Искусственно насимулируем эксперимент, который мог бы произойти в реальности. В этот раз это будут не два равномерных распределения, а что-то более приближенное к реальности, и что вы сможете проверить самостоятельно, запустив код.
Пусть распределение ненулевой части метрики подчиняется экспоненциальному распределению. Для выручки это хорошее приближение.

Пусть нашими скидками мы увеличили число платящих пользователей на 5%.
Изначально в контроле было 50% нулей. Половина пользователей ничего не покупали на сайте.
В тесте стало 55% платящих пользователей.
Раньше пользователь в среднем платил 7 рублей, а сейчас из-за скидки он платит 6 ₽, скидка была примерно 15%. Тогда математическое ожидание выручки в контроле было 3.5 ₽ (7 * 0.5), а в тесте — 3.3 ₽ (6 * 0.55).
То есть платящих пользователей стало больше, а средний чек упал. А значит, верна H0 и процент ложноположительных срабатываний не может быть больше 5% у корректного критерия. Для проверки мы снова запустим тест 1000 раз и проверим, что здесь покажут T-test с Манном-Уитни.
Демонстрация результатов:
# Подключим библиотеки
import scipy.stats as sps
from tqdm.notebook import tqdm # tqdm – библиотека для визуализации прогресса в цикле
from statsmodels.stats.proportion import proportion_confint
import numpy as np
# Заводим счетчики количества отвергнутых гипотез для Манна-Уитни и для t-test
mann_bad_cnt = 0
ttest_bad_cnt = 0
sz = 10000
for i in tqdm(range(sz)):
test_zero_array = sps.bernoulli(p=0.55).rvs(1000)
control_zero_array = sps.bernoulli(p=0.5).rvs(1000)
test = sps.expon(loc=0, scale=6).rvs(1000) * test_zero_array # ET = 3.3
control = sps.expon(loc=0, scale=7).rvs(1000) * control_zero_array # EC = 3.5
# Проверяем гипотезу
mann_pvalue = sps.mannwhitneyu(control, test, alternative='less').pvalue
ttest_pvalue = sps.ttest_ind(control, test, alternative='less').pvalue
if mann_pvalue < 0.05:
mann_bad_cnt += 1
if ttest_pvalue < 0.05:
ttest_bad_cnt += 1
# Строим доверительный интервал
left_mann_power, right_mann_power = proportion_confint(count = mann_bad_cnt, nobs = sz, alpha=0.05, method='wilson')
left_ttest_power, right_ttest_power = proportion_confint(count = ttest_bad_cnt, nobs = sz, alpha=0.05, method='wilson')
# Выводим результаты
print(f"Mann-whitneyu LESS power: {round(mann_bad_cnt / sz, 4)}, [{round(left_mann_power, 4)}, {round(right_mann_power, 4)}]")
print(f"T-test LESS power: {round(ttest_bad_cnt / sz, 4)}, [{round(left_ttest_power, 4)}, {round(right_ttest_power, 4)}]")Результат:
Mann-whitneyu LESS power: 0.3232, [0.3141, 0.3324]
T-test LESS power: 0.0072, [0.0057, 0.0091]Процент принятий гипотезы H1: «средний чек вырос» у T-test около 0: это нормально, так как мы знаем, что на самом деле среднее в тесте упало, а не выросло — критерий корректен. А у Манна-Уитни процент отвержений 32%, что сильно больше 11%, которые были в первом, изначальном примере.
Представим, что на ваших настоящих данных была примерно такая же картина. Только в реальности вы не симулировали эксперимент, поэтому не знаете, что ваш средний чек упал. У T-test околонулевой процент обнаружения статистически значимого эффекта. Используя его, вы видите, что он ничего не задетектировал, начинаете использовать критерий Манна-Уитни, и в одной трети случаев обнаруживаете эффект, что среднее увеличилось.
Увидев, что T-test не прокрасился, а Манн-Уитни даёт статистически значимый прирост, многие аналитики доверятся второму критерию и покатят на всех пользователей скидки. И выручка упадёт.
Кейс 2: отток части пользователей
Другой вариант: части пользователей не понравилось наше изменение и они ушли. Допустим, мы захотели нарастить количество сделок на Авито. Сделка у нас — событие, когда продавец нашёл покупателя на своё объявление. Для этого мы добавили новые обязательные параметры в объявление и процесс подачи стал сложнее. Часть продавцов отвалилась, зато остальным стало легче: теперь покупателям с помощью фильтров и поиска проще находить подходящие объявления. Осталось понять, нарастили ли мы количество сделок.
Например, у нас было 100 продавцов и в среднем они совершали 2 сделки на Авито. После того как мы ввели новые параметры, продавцов стало 70. Оставшимся 30 продавцам наша инициатива не понравилась и они ушли. Теперь на одного продавца приходится по 3 сделки, так как пользователям стало легче находить релевантный товар. Раньше было 200 сделок, а теперь 210.
В этот раз все распределения будут взяты не из теоретических соображений, а из реальных данных. Как это сделать, я подробно рассказывал в статье про улучшение A/B-тестов. Я собрал 1000 настоящих А/А-тестов на исторических данных в Авито: взял всех продавцов в разных категориях и регионах за разные промежутки времени и поделил случайно на тест и контроль. Повторил это 1000 раз.
Теперь я хочу простимулировать эффект от ввода новых обязательных параметров в тестовой группе: я моделирую отток пользователей и прирост числа сделок у оставшихся продавцов.
Как именно я это сделал:
взял в качестве метрики количество сделок;
обнулил число сделок 5 процентам случайных продавцов, как будто они ушли с площадки;
у оставшихся пользователей в тестовой группе я домножил количество сделок на некий коэффициент больше единицы. В итоге среднее число сделок на продавца стало больше даже с учетом оттока. В примере выше этот коэффициент равнялся бы 1.5: 2 сделки → 3 сделки.
На самом деле количество сделок выросло от введения новых параметров.
Замечание
Да, получились не совсем «реальные» AB-тесты, а лишь приближения к ним. Но в любом случае это наилучшее возможное приближение, где мы знаем реальный эффект.
Теперь построим таблицу процента отвержений нулевой гипотезы в зависимости от альтернативы на этих 1000 A/B-тестах:
в тесте количество сделок больше, чем в контроле | --//-- меньше, чем в контроле | |
T-test | 27% | 0.1% |
Манн-Уитни | 6% | 80% 🤬 |
Мы видим, что T-test в 27% случаев отвергает гипотезу в нужную сторону. Манн-Уитни — только в 6% случаев. Как видим, тут мощность (или чувствительность) Манна-Уитни меньше, чем у T-test. Если бы мы поставили корректную гипотезу «количество сделок выросло» для проверки, то мощность Манна-Уитни была бы меньше, чем у T-test.
Но если проверять, не уменьшили ли мы количество сделок новыми параметрами, то тут нас поджидает беда: в 80% случаев Манн-Уитни задетектирует эффект.
Если бы мы использовали этот критерий на практике, то Манн-Уитни увидел бы тут отток числа сделок. Тогда в 4 из 5 тестов мы бы не катили новые фильтры на Авито и сделали вывод, что новые параметры при подаче только отбирают у нас контент и не помогают покупателям находить интересующие товары.
Благодаря Манну-Уитни мы делаем неверный вывод о наших данных. 11% ложных прокрасов в 1 примере — это не предел. В реальных A/B-тестах их может быть сильно больше.
Вспомним, почему критерий Манна-Уитни популярен:
В данных часто бывает много шумов и выбросов, поэтому T-test неприменим
по соображениям мощности, чувствительности или ненормальности данных.
А Манн-Уитни в этот момент отлично срабатывает и более вероятно находит статистически значимый эффект.
Как видно, это предположение не соответствует действительности:
T-test везде показал себе корректно и не делал больше ложноположительных прокрасов, чем должен был. А как это происходит и почему на самом деле критерий корректен, вы можете прочесть всё в той же статье про улучшение A/B-тестов.
Манн-Уитни нас не спасает, а делает только больше ложноположительных прокрасов. С тем же успехом можно кидать монетку и отвергать гипотезу, если выпала решка. Во втором кейсе монетка ошиблась бы в 50% случаев, а Манн-Уитни ошибается в 80%.
Здесь же кроется самая главная беда этого критерия: Манн-Уитни сильно чаще обнаруживает эффект, чем T-test. Именно поэтому этот критерий стал популярен у аналитиков. Когда есть выбор:
проглотить «горькую» пилюлю и получить не статистически значимые результаты с помощью T-test;
поверить критерию Манну-Уитни, что эффект на самом деле есть;
то хочется верить последнему. И в этот момент аналитики ошибаются. Поэтому мы в Авито не используем критерий Манна-Уитни.
Замечания про примеры
Это, конечно, всё хорошо, но я рассмотрел два специфических случая, когда метрика конверсии не сонаправлена с финальной метрикой. Например, в примере со скидками: конверсия в покупку выросла, а среднее по выручке упало. Кажется, что более частая картина, когда конверсия выросла и ARPU выросло. В этом случае, вы могли бы вместо проверки прироста ARPU перейти к проверке роста конверсий — менее шумной метрике. Но, к сожалению, вы не знаете, так ли это на самом деле, поэтому вы не можете полагаться на это :( А значит два примера выше вполне могут иметь место в реальности.
Ещё Манна-Уитни любят применять для медиан. Здесь также можно привести примеры, почему это невалидно. В этом случае я советую пользоваться Bootstrap, который корректно работает на больших выборках. Или реализовать критерий из этой статьи.
Логарифмирование метрики
Для работы с выбросами в данных часто советуют идею логарифмирования метрики. Алгоритм состоит из двух частей:
применим y := log(x + 1);
к новым логарифмированным метрикам «y» применим T-test.
Зачем используют этот метод? Когда в данных есть выбросы, метрика очень шумная и дисперсия в данных огромная. А при логарифмировании выбросы исчезают и все данные становятся примерно одинаковыми.
Проверим критерий на том же искусственном примере что и ранее.
Код
# Подключим библиотеки
import scipy.stats as sps
from tqdm.notebook import tqdm # tqdm – библиотека для визуализации прогресса в цикле
from statsmodels.stats.proportion import proportion_confint
import numpy as np
# Заводим счетчики количества отвергнутых гипотез для t-test
ttest_bad_cnt = 0
sz = 10000
for i in tqdm(range(sz)):
test_zero_array = sps.bernoulli(p=0.45).rvs(1000)
control_zero_array = sps.bernoulli(p=0.5).rvs(1000)
test = sps.expon(loc=0, scale=7).rvs(1000) * test_zero_array # ET = 3.15
control = sps.expon(loc=0, scale=6).rvs(1000) * control_zero_array # EC = 3
test = np.log(test + 1)
control = np.log(control + 1)
ttest_pvalue = sps.ttest_ind(control, test, alternative='greater').pvalue
if ttest_pvalue < 0.05:
ttest_bad_cnt += 1
# Строим доверительный интервал
left_ttest_power, right_ttest_power = proportion_confint(count = ttest_bad_cnt, nobs = sz, alpha=0.05, method='wilson')
# Выводим результаты
print(f"Log T-test GREATER power: {round(ttest_bad_cnt / sz, 4)}, [{round(left_ttest_power, 4)}, {round(right_ttest_power, 4)}]")
Результат лучше, чем у Манна-Уитни: количество отвержений не в ту сторону всего 15% вместо 38%. Но это всё ещё значит, что этой штукой пользоваться нельзя!
Почему этот критерий неверен — рассмотрим на примере выборки из трёх элементов: a, b, c.
Метрика, которая нас интересует — это среднее (a + b + c) / 3. Именно её рост или падение мы хотим задетектировать. При логарифмировании мы считаем метрику (abc) ^ 1/3, или среднее геометрическое. Среднее и среднее геометрическое — разные метрики, поэтому критерий ошибается.
С точки зрения бизнеса логика такая: прирост более мелких значений в такой метрике сильнее детектируется, чем прирост у больших значений. Например:
Раньше значение метрики было 0, а сейчас 2. log(2 + 1) - log(1) ≈ 1.09
Раньше значение метрики было 1000, а сейчас 2000. log(2001) - log(1001) ≈ 0.69
То есть, прирост метрики на 2 даёт больший вклад, чем прирост метрики на 1000. Поэтому у нас и получается фигня при использовании критерия. Но все выбросы при этом становятся меньше и поэтому критерий имеет лучшую мощность.
Когда Манн-Уитни работает?
Если тестируемая фича полностью сдвигает выборку на некий коэффициент theta или масштабирует выборку на некий параметр theta (theta > 0), то критерий Манна-Уитни применим, и он будет верно оценивать направление сдвига математического ожидания.
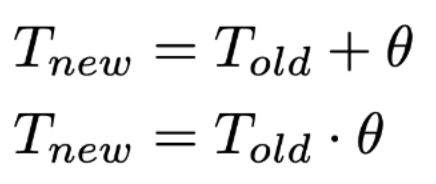
Доказательство корректности Манна-Уитни в более общем случае
Попробуем рассуждать в более общем случае. Если вы знаете, что ваше тестируемое изменение полностью сдвинуло функцию распредления в тесте, то можно использовать критерий Манна-Уитни. То есть, если возможны только три варианта:

Тогда вы можете использовать критерий Манна-Уитни. Что значит функция распределения F больше функции распределения G? Это верно, если в любой точке x: F(x) > G(x).
Итого: если воздействие хоть как-то повлияло на юзеров и функция распределения полностью сдвигается, вы можете использовать критерий Манна-Уитни. То же самое вы можете сделать, если одно распределение будет доминировать над другим. Правда вот как вы будете уверены, что у вас именно такая ситуация?
Я утверждаю, что если F_T доминирует над F_C, то:
P(C < T) <= 1/2, а значит статистика Манна-Уитни будет смещена от нормального состояния
ET < EC
Сначала покажем второй факт:

Где первый переход следует из свойств мат. ождидания, а неравество следует из того, что в любой точке x: F_T(x) > F_C(x). А значит 1 - F_T(x) < 1 - F_C(x).
Так что если Манн-Уитни умеет верно детектировать, какое распределение доминирует над другим, то он умеет правильно детектировать рост или падение мат. ожидания. И здесь как раз нам поможет первый факт.
Докажем, что P(C < T) <= 1/2. Тогда это значит, что статистика Манна-Уитни при таком доминировании всегда будет смещена только в одну сторону. А значит, если односторонний критерий Манна-Уитни отвергся => ET < EC.
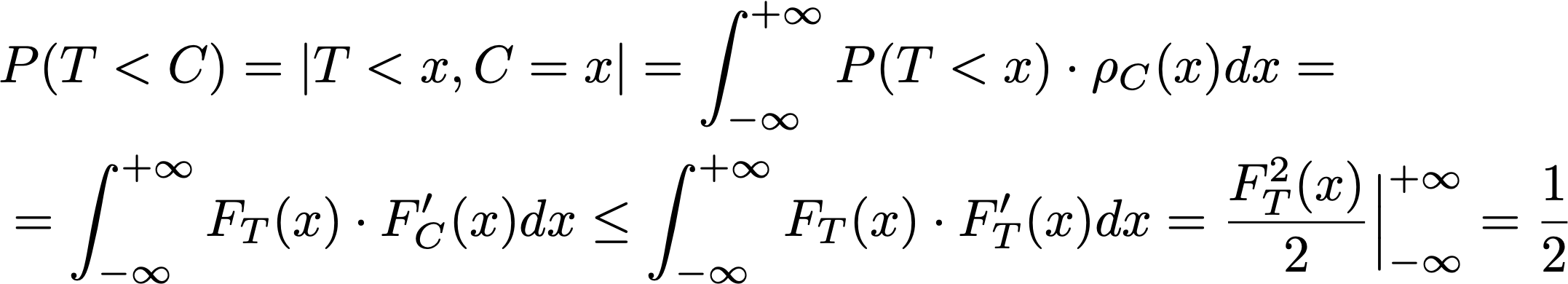
То есть Манн-Уитни умеет проверять прирост/падение средних при сдвиге распределений. А теперь одно из распределений будет доминировать над другим: когда вы сдвигаете распределение или масштабируете его, то у вас как раз один из случаев, описанных выше. Поэтому вы можете в этих случаях пользоваться критерием Манна-Уитни.
Вопрос: каким образом вы будете уверены, что у вас именно такой эффект от воздействия? Если вы можете привести пример реальной задачи в бизнесе с таким эффектом от тестируемого изменения — жду вас в комментариях к статье :)
Даже если вы знаете, что у вас именно будет такой эффект, вместо Манна-Уитни я бы предложил использовать критерий однородности Колмогорова-Смирнова, который также может смотреть односторонние альтернативы и показывать направление сдвига мат. ожидания. Только в этот момент:
мощность у Колмогорова-Смирнова при сдвиге или масштабировании метрики не меньше, чем у Манна-Уитни. А где-то даже больше.
вы точно знаете, что изначальная гипотеза у вас — равенство распределений, а не странные интерпретации, присущие Манну-Уитни. А значит, у вас меньше шанс неправильно осознать результаты.
На втором пункте я предлагаю остановиться: я сравню Манна-Уитни и Колмогорова-Смирнова по мощности — в случае сдвига выборки в тесте и в случае масштабирования.
Код
# Подключим библиотеки
import scipy.stats as sps
from tqdm.notebook import tqdm # tqdm – библиотека для визуализации прогресса в цикле
from statsmodels.stats.proportion import proportion_confint
import numpy as np
# Заводим счетчики количества отвергнутых гипотез для Манна-Уитни, t-test, KS
mann_bad_cnt = 0
ks_bad_cnt = 0
ttest_bad_cnt = 0
sz = 10000
for i in tqdm(range(sz)):
test = sps.expon(loc=0, scale=10).rvs(1000)
control = sps.expon(loc=0, scale=10).rvs(1000)
test += 0.5
mann_pvalue = sps.mannwhitneyu(control, test, alternative='less').pvalue
ks_pvalue = sps.ks_2samp(control, test, alternative='greater').pvalue # Потому что он сравнивает F_T > F_C. А в этот момент ET < EC. Поэтому и другая альтернатива
ttest_pvalue = sps.ttest_ind(control, test, alternative='less').pvalue
if mann_pvalue < 0.05:
mann_bad_cnt += 1
if ks_pvalue < 0.05:
ks_bad_cnt += 1
if ttest_pvalue < 0.05:
ttest_bad_cnt += 1
# Выводим результаты
print(f"Mann-whitneyu: {round(mann_bad_cnt / sz, 4)}")
print(f"Kolmogorov-Smirnov: {round(ks_bad_cnt / sz, 4)}")
print(f"T-test: {round(ttest_bad_cnt / sz, 4)}")Mann-whitneyu: 0.6027
Kolmogorov-Smirnov: 0.7074
T-test: 0.2984Как видим, выиграл Колмогоров-Смирнов.
А теперь посмотрим на случай, когда происходит масштабирование. На экспоненциальном распределении разницы в мощности не было обнаружено — можете сами провести эксперимент и убедиться. Поэтому ради интереса я взял исторические данные Авито, создал 1000 тестов и помножил выручку в тесте на коэффициент больше единицы. Примерно то же самое мы делали во втором кейсе ранее, но без обнуления метрики у части пользователей.
Mann-whitneyu: 0.5778
Kolmogorov-Smirnov: 0.9949
T-test: 0.0798И здесь Колмогоров-Смирнов победил.
А поэтому вопрос к вам: зачем использовать критерий Манна-Уитни? Лучше попробуйте критерий Колмогорова-Смирнова.
Выводы
Итого, Манн-Уитни:
Это критерий однородности. Все остальные интерпретации нулевой гипотезы неверны.
В реальных задачах этот критерий неприменим. Если вы начнете его использовать, то он обнаружит статистически значимый эффект в большем числе случаев, чем у T-test. Только после этого неверно говорить о приросте математического ожидания или медианы в тесте относительно контроля. И именно частые прокрасы критерия Манна-Уитни делают его самым опасным и таким популярным критерием для анализа A/B-тестов.
Логарифмирование метрики при этом тоже не работает.
Если вы точно знаете, что ваше воздействие сдвинуло вашу выборку или отмасштабировало её на некий параметр, то вы можете использовать Манна-Уитни. Но зачем, если есть критерий Колмогорова-Смирнова, который мощнее?
И главное: в реальности такой ситуации не бывает в бизнесовых задачах. А если вы знаете такие примеры, то будет очень интересно пообщаться с вами.
Если есть вопросы, желание обсудить статью, да и вообще любая реакция, то жду вас в комментариях!
Предыдущая статья: Сколько нужно времени, чтобы переписать объявление?
