Возможность генерировать данные с заданной корреляцией очень важна для моделирования. В R ожидаемо обширный набор инструментов — пакетов и функций для генерации и визуализации данных из многомерных распределений. Базовая функция для генерации многомерных нормально распределенных данных —
Блок кода ниже генерирует 5000 выборок из двумерного нормального распределения со средним (0, 0) и ковариационной матрицей Сигма, приведенной в коде. Функция
R предлагает несколько способов визуализации распределения. Следующие две строчки кода накладывают контурный график на тепловую карту, которая ставит в соответствие плотности точек градиент цветов.

На графике видны неправильные контуры симулированных данных. Код ниже, использующий функцию
Следующий кусочек кода генерирует парочку трехмерных графиков поверхности. Второй — график rgl, который можно вращать и смотреть под разными углами непосредственно на экране.
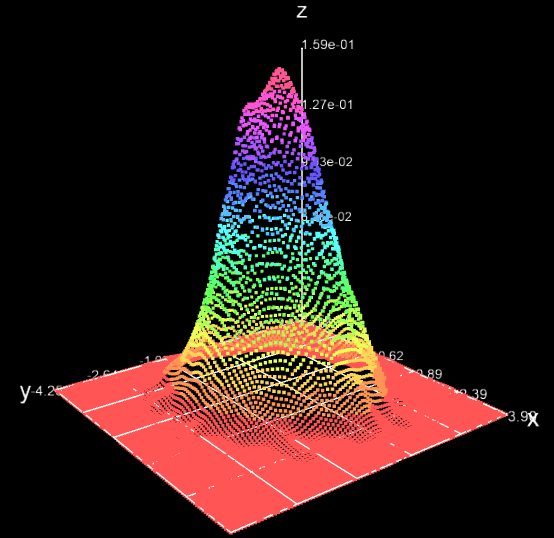
Теперь напишем немного кода, чтобы получить значения x, y и z из табличных координат ядровой оценки плотности распределения. Они позволят построить поверхность с помощью новой функции scatterplot3js() из htmlwidgets, javascript-пакета threejs. Эта визуализация изображает поверхность не с таким уровнем детализации, как график rgl. Тем не менее, она показывает некоторые основные функции pdf и обладает существенным преимуществом — легко встраиваться в веб-страницы. Полагаю, графики в виде html-виджетов будет проще и легче использовать.
Код ниже использует функцию

Настоящая ценность многомерных функций распределения с точки зрения науки о данных — симулировать наборы данных с более чем двумя переменными. Функции, предлагаемые выше, подходят для решения этой задачи, но есть некоторые технические соображения и, конечно, не будет доступна визуализация. Кусочек кода ниже генерирует 10 переменных из многомерного нормального распределения с заданной ковариационной матрицей. Обратите внимание, для генерации ковариационной матрицы использовалась функция
После генерации матрицы я использую функцию
Наконец, что же на счет других многомерных распределений, отличных от нормального и t-распределения? R предлагает несколько функций, как, например,
mvrnorm() из пакета MASS, части R, хотя пакет mvtnorm также предлагает функции для симуляции и многомерного нормального, и t-распределения.Блок кода ниже генерирует 5000 выборок из двумерного нормального распределения со средним (0, 0) и ковариационной матрицей Сигма, приведенной в коде. Функция
kde2d(), также из пакета MASS, генерирует двумерную ядровую оценку плотности распределения.# СИМУЛЯЦИЯ МНОГОМЕРНЫХ ДАННЫХ
# https://stat.ethz.ch/pipermail/r-help/2003-September/038314.html
# Сначала симулируем двумерную нормальную выборку
library(MASS)
# Симулируем двумерные нормальные данные
mu <- c(0,0) # Среднее
Sigma <- matrix(c(1, .5, .5, 1), 2) # Ковариационная матрица
# > Sigma
# [,1] [,2]
# [1,] 1.0 0.1
# [2,] 0.1 1.0
# Сгенерируем выборку из N(mu, Sigma)
bivn <- mvrnorm(5000, mu = mu, Sigma = Sigma ) # из пакета MASS
head(bivn)
# Посчитаем ядровую оценку плотности распределения
bivn.kde <- kde2d(bivn[,1], bivn[,2], n = 50) # из пакета MASS
R предлагает несколько способов визуализации распределения. Следующие две строчки кода накладывают контурный график на тепловую карту, которая ставит в соответствие плотности точек градиент цветов.
# Результаты в виде контурного графика, наложенного на тепловую карту
image(bivn.kde) # из базового графического пакета
contour(bivn.kde, add = TRUE) # из базового графического пакета
На графике видны неправильные контуры симулированных данных. Код ниже, использующий функцию
ellipse() из пакета ellipse, генерирует классический график двумерного нормального распределения, встречающийся во многих учебниках.# Классический график двумерного нормального распределения
library(ellipse)
rho <- cor(bivn)
y_on_x <- lm(bivn[,2] ~ bivn[,1]) # Регрессия Y ~ X
x_on_y <- lm(bivn[,1] ~ bivn[,2]) # Регрессия X ~ Y
plot_legend <- c("99% ДИ зеленый", "95% ДИ красный","90% ДИ синий",
"Y на X черный", "X на Y коричневый")
plot(bivn, xlab = "X", ylab = "Y",
col = "dark blue",
main = "Двумерное нормальное распределение с доверительными интервалами")
lines(ellipse(rho), col="red") # ellipse() из пакета ellipse
lines(ellipse(rho, level = .99), col="green")
lines(ellipse(rho, level = .90), col="blue")
abline(y_on_x)
abline(x_on_y, col="brown")
legend(3,1,legend=plot_legend,cex = .5, bty = "n")
Следующий кусочек кода генерирует парочку трехмерных графиков поверхности. Второй — график rgl, который можно вращать и смотреть под разными углами непосредственно на экране.
# Трехмерная поверхность
# Базовый перспективный график
persp(bivn.kde, phi = 45, theta = 30, shade = .1, border = NA) # из базового графического пакета
# Интерактивный график RGL
library(rgl)
col2 <- heat.colors(length(bivn.kde$z))[rank(bivn.kde$z)]
persp3d(x=bivn.kde, col = col2)
Теперь напишем немного кода, чтобы получить значения x, y и z из табличных координат ядровой оценки плотности распределения. Они позволят построить поверхность с помощью новой функции scatterplot3js() из htmlwidgets, javascript-пакета threejs. Эта визуализация изображает поверхность не с таким уровнем детализации, как график rgl. Тем не менее, она показывает некоторые основные функции pdf и обладает существенным преимуществом — легко встраиваться в веб-страницы. Полагаю, графики в виде html-виджетов будет проще и легче использовать.
# threejs Javascript-график
library(threejs)
# Извлекаем данные из формата таблицы kde
x <- bivn.kde$x; y <- bivn.kde$y; z <- bivn.kde$z
# Строим координаты x,y,z
xx <- rep(x,times=length(y))
yy <- rep(y,each=length(x))
zz <- z; dim(zz) <- NULL
# Устанавливаем спектр цветов
ra <- ceiling(16 * zz/max(zz))
col <- rainbow(16, 2/3)
# Интерактивный 3D-график рассеяния
scatterplot3js(x=xx,y=yy,z=zz,size=0.4,color = col[ra],bg="black")

Код ниже использует функцию
rtmvt() из пакета tmvtnorm для генерации двумерного t-распределения. График rgl изображает поверхность ядровой оценки плотности распределения в деталях.# Выборка с возвратом из многомерного t-распределения
library (tmvtnorm)
Sigma <- matrix(c(1, .1, .1, 1), 2) # Ковариационная матрица
X1 <- rtmvt(n=1000, mean=rep(0, 2), sigma = Sigma, df=2) # из пакета tmvtnorm
t.kde <- kde2d(X1[,1], X1[,2], n = 50) # из пакета MASS
col2 <- heat.colors(length(bivn.kde$z))[rank(bivn.kde$z)]
persp3d(x=t.kde, col = col2)
Настоящая ценность многомерных функций распределения с точки зрения науки о данных — симулировать наборы данных с более чем двумя переменными. Функции, предлагаемые выше, подходят для решения этой задачи, но есть некоторые технические соображения и, конечно, не будет доступна визуализация. Кусочек кода ниже генерирует 10 переменных из многомерного нормального распределения с заданной ковариационной матрицей. Обратите внимание, для генерации ковариационной матрицы использовалась функция
genPositiveDefmat() из пакета clusterGeneration. Это потому, что функция mvrnorm() выдаст ошибку, как теоретически должно произойти, если ковариационная матрица не положительно определена, и подбор комбинации элементов многомерной матрицы, чтобы сделать ее положительно определенной, потребует порядочно удачи и времени на вычисления.После генерации матрицы я использую функцию
corrplot() из пакета corrplot, чтобы вывести красивый график попарных корреляций, определяемых цветом и формой. corrplot() неплохо масштабируется с увеличением числа переменных и выдаст приличный результат для 40-50 переменных. (К сведению, сейчас ggcorrplot используется для ggplot2-графиков.) Можно использовать другие опции для построения попарных графиков рассеяния, и R предлагает множество альтернатив.#Многомерные распределения
library(corrplot)
library(clusterGeneration)
mu <- rep(0,10)
pdMat <- genPositiveDefMat(10,lambdaLow=10)
Sigma <- pdMat$Sigma
dim(Sigma)
mvn <- mvrnorm(5000, mu = mu, Sigma = Sigma )
corrplot(cor(mvn),
method="ellipse",
tl.pos="n",
title="Матрица корреляций")
Наконец, что же на счет других многомерных распределений, отличных от нормального и t-распределения? R предлагает несколько функций, как, например,
rlnorm() из пакета compositions, которая генерирует случайные переменные из многомерного логнормального распределения. Ими так же легко пользоваться, как и mvrorm(), но ей подобные придется поискать. Думаю, более плодотворный подход, если вам действительно необходимо работать с распределениями вероятности — познакомиться с пакетом copula.