
Привет! На связи команда геоинформационных систем «Магнита». Мы начинаем серию очерков о модели прогнозирования продаж в новых магазинах. В первой статье расскажем про один из наиболее значимых признаков модели — балл Хаффа. Мы постараемся описать теоретическую сторону и покажем реальные примеры решения возникающих сложностей. Надеемся, эта статья предоставит ценные идеи и информацию для ваших задач, будь вы опытный специалист или новичок. Итак, приступим!
При прогнозировании товарооборота в новых локациях мы учитываем множество факторов и нелинейных зависимостей, чтобы снизить количество ошибок в расчётах и минимизировать риск неэффективных инвестиций в открытие новых магазинов. В классическом продуктовом ритейле основополагающим фактором успеха является локация: близость к потенциальному покупателю, наличие точек интереса и конкурентное окружение. Эти признаки легли в основу балла Хаффа.
Обзор основных моделей прогнозирования
Идея, что покупатели идут туда, где ближе и больше товара, не выглядит слишком сложной. Но как это обычно бывает, проблема заключается в формализации интуитивных закономерностей. Двадцатый век выделяется динамичной деятельностью в этом вопросе, основные этапы которой представлены ниже.
Гравитационная модель Рейли
Согласно «закону притяжения в ритейле» Рейли центры торговли привлекают покупателей из соседних населённых пунктов пропорционально численности населения и обратно пропорционально расстоянию между ними.
Bi — доля покупателей, «притягиваемых» из некоторого промежуточного населенного пункта в центр торговли ?
Pi — численность населённого пункта ?, ассоциированного с соответствующим центром торговли
Di — расстояние от некоторого промежуточного населённого пункта до центра торговли ?
Зависимость от численности населения — линейная. Эмпирическая оценка степени при расстоянии равна 2 аналогично закону притяжения Ньютона. Привлекательность центра торговли выражается в численности населения, проживающего в городе его нахождения или же в его окрестности, что является опосредованной мерой объёма и качества товара.
Модель критической точки Конверса
Из модели Рейли и понятия «критической точки» — точки между населенными пунктами, в которой покупатели делятся поровну — логически вытекает модель Конверса. К сожалению, ничего совершенно нового относительно модели Рейли мы здесь не обнаружим.
??→? — критическая точка от населённого пункта ? до населённого пункта ?
? — расстояние между ? и ?
?? — численность населённого пункта ?, ассоциированного с соответствующим центром торговли
Обратная модель критической точки Мейера и Мэйсона
На первый взгляд кажется, что данная модель ошибочно повторяет модель Конверса и в записи просто перепутаны местами буквы, но всё не так просто. Идея в том, что с развитием транспортной доступности и логистики в современном мире потенциальному покупателю проще преодолевать большие расстояния. В нашем случае обратная модель критической точки найдёт своё применение в том, что в малых населённых пунктах радиус притяжения торговой точки выше, чем в крупных населённых пунктах.
Модель Хаффа
Главный герой статьи — модель Хаффа, в которой учитывается влияние множества торговых центров, а главное — в ней уже используется вероятностное поведение покупателя.
??? — вероятность, что покупатель в локации ? отправится в торговый центр ?
?? — площадь торговой точки ?
??? — время, за которое покупатель достигает торговой точки ? из локации ?
? — параметр, отражающий влияние времени в пути на поведение покупателя
E?? — предполагаемое количество покупателей из локации ?, которые отправятся в торговую точку ?
??? — вероятность, что покупатель в локации ? отправится в торговую точку ?
?? — количество покупателей в локации ?
Обзор модели Хаффа
Модель Хаффа предсказывает поток между двумя точками (в общем случае — между множеством точек) на основе количества потенциальных покупателей или других учитываемых потребителей в каждой торговой точке и обратно пропорциональна некоторому показателю расстояния или времени в пути между точками. Однако модель также вводит новую концепцию «привлекательности», которая измеряет вероятность посещения объекта потенциальными покупателями при равных внешних условиях. Эта привлекательность может определяться такими факторами, как внутренние показатели торговой точки (чистота, очереди на кассах, наличие ценников, ассортиментная матрица и т. д.) или экономической активностью в локации, доступностью услуг или удобств, а также общей привлекательностью локации в качестве места назначения.
Одно из ключевых отличий модели Хаффа — введение переменной, называемой «гравитационный потенциал» или «балл Хаффа» (как мы его называем). Это мера общих сил притяжения в определённом месте. Она позволяет лучше понять потоки в локации и оценить потенциальное распределение жителей между торговыми объектами с разным уровнем привлекательности.
У модели Хаффа есть и ограничения. Предполагается, что поток однороден, люди или товары — единственные факторы, которые нужно учитывать, а влияет на поток только расстояние. Комплексное влияние других факторов учитывается в интегральном коэффициенте привлекательности торговой точки, и определение этого влияния — одна из наиболее сложных задач в калибровке модели.
Теперь соберём все наши теоретические знания и оформим их в список допущений и ограничений, которые мы будем в дальнейшем использовать.
Скорость всех потенциальных покупателей в рамках нашей задачи принимаем одинаковой, в силу чего время пути покупателя от места жительства до торговой точки заменяем на расстояние.
Чем больше торговая площадь, тем сильнее притяжение торговой точки, её привлекательность для потенциального покупателя. Тем самым торговая площадь является количественным выражением ассортимента товаров. Для учёта качества предоставляемых услуг привлекательность торговой точки и бренда в общем может корректироваться с помощью дополнительных коэффициентов, описывающих специфику моделируемой области.
Используется классическое влияние расстояния с параметром ?=2
Чем больше численность населённого пункта, тем меньше зона влияния торговой точки. Всё согласно обратной модели критической точки, которая подтверждается анализом статистики карт лояльности «Магнит».
Итоговое количество семей, привлекаемых конкретной торговой точкой, рассчитывается по всем жилым домам с учётом конкурентной среды в рамках заданной зоны влияния.
Использование балла Хаффа в «Магните»
Для решения наших задач мы работаем с данными по домам и графами дорог. Мы используем коммерческие и бесплатные источники геоданных, которые приоритезируются в зависимости от качества, актуальности, покрытия.
Один из важнейших этапов в расчёте — валидация и обогащение геоданных ответственной за это командой. Для небольших магазинов ошибка даже в одном графе дорог может иметь драматические последствия. К слову сказать, собственных геоданных в «Магните» порядка 10–15% от всей географии сети — от Смоленска до Иркутска.
Далее привязываем жилые дома к дорожному графу. Самый простой сценарий при наличии данных о входах — «посадить» здание входом на ближайшую по прямой дорогу. Если данных о входах нет, здания «садятся» каждой своей стороной на ближайшую из дорог. Для зданий с большой площадью подложки без данных о входах симулируется равномерное распределение искусственных входов по периметру, относительно которых выполняется посадка до ближайших дорог. Важно учитывать естественные ограничения и максимальное расстояние до ближайших дорог, дабы исключить случаи посадки через реки, железнодорожное полотно и поля.
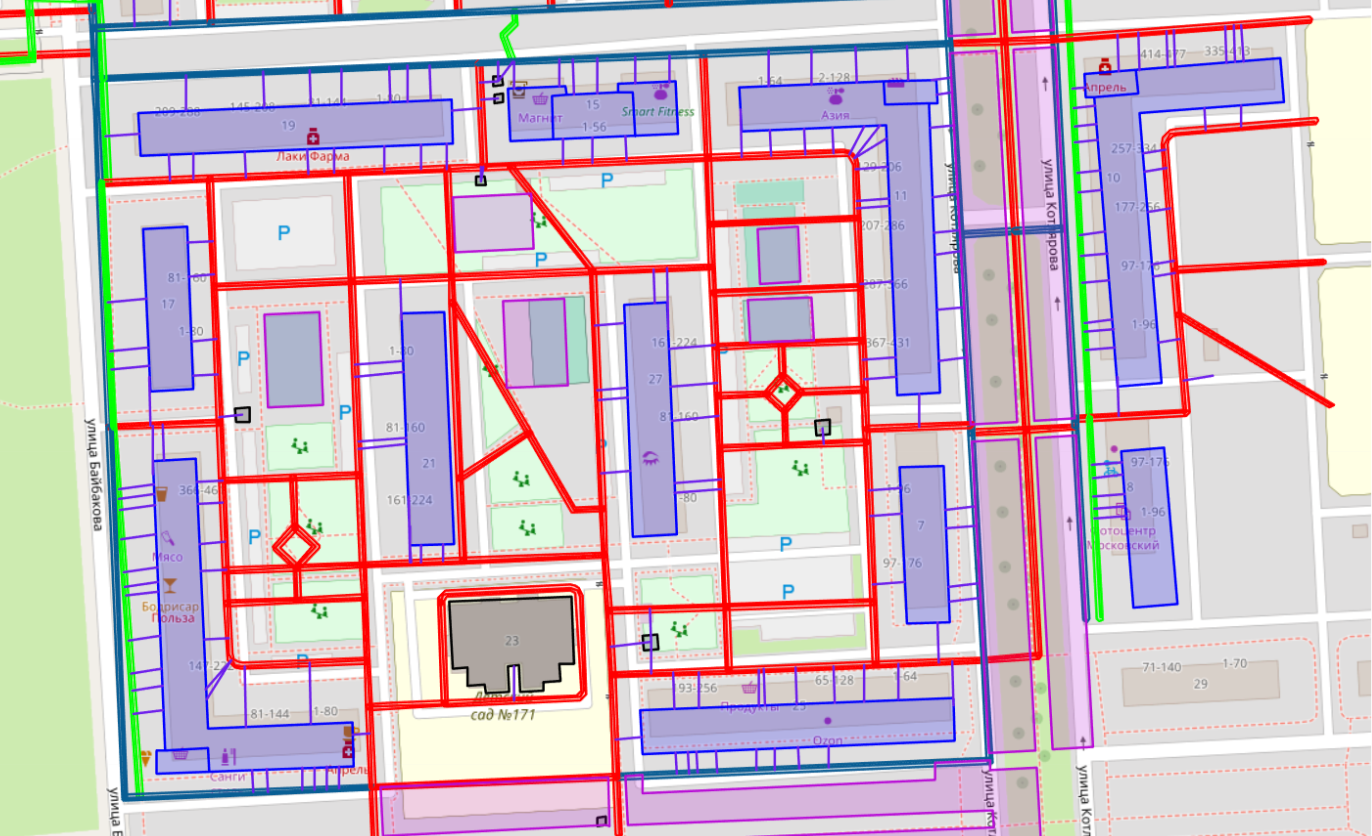
Затем рассчитываем расстояния и штрафы. Для расчёта пешеходного трафика в модели Хаффа используется соответствующий граф дорог. При этом для симуляции затрат времени на переход покупателем дорог используются дополнительные «штрафные» расстояния, тем самым здания через дорогу оказываются дальше, чем аналогичные в плане расстояния дома на той стороне дороги. Данные «штрафы» откалиброваны в результате работы команды продукта в «полях».
Делаем отладку параметров. Такие параметры, как радиус влияния и привлекательность конкретных торговых точек настраиваются с помощью аналитики внутренних данных по картам лояльности и дальнейшим распространением логики на всё конкурентное окружение.
На выходе получаем зоны влияния. Пример ниже — полигон, покрывающий дома с ненулевой вероятностью, что жители этого дома пойдут в объект прогноза.
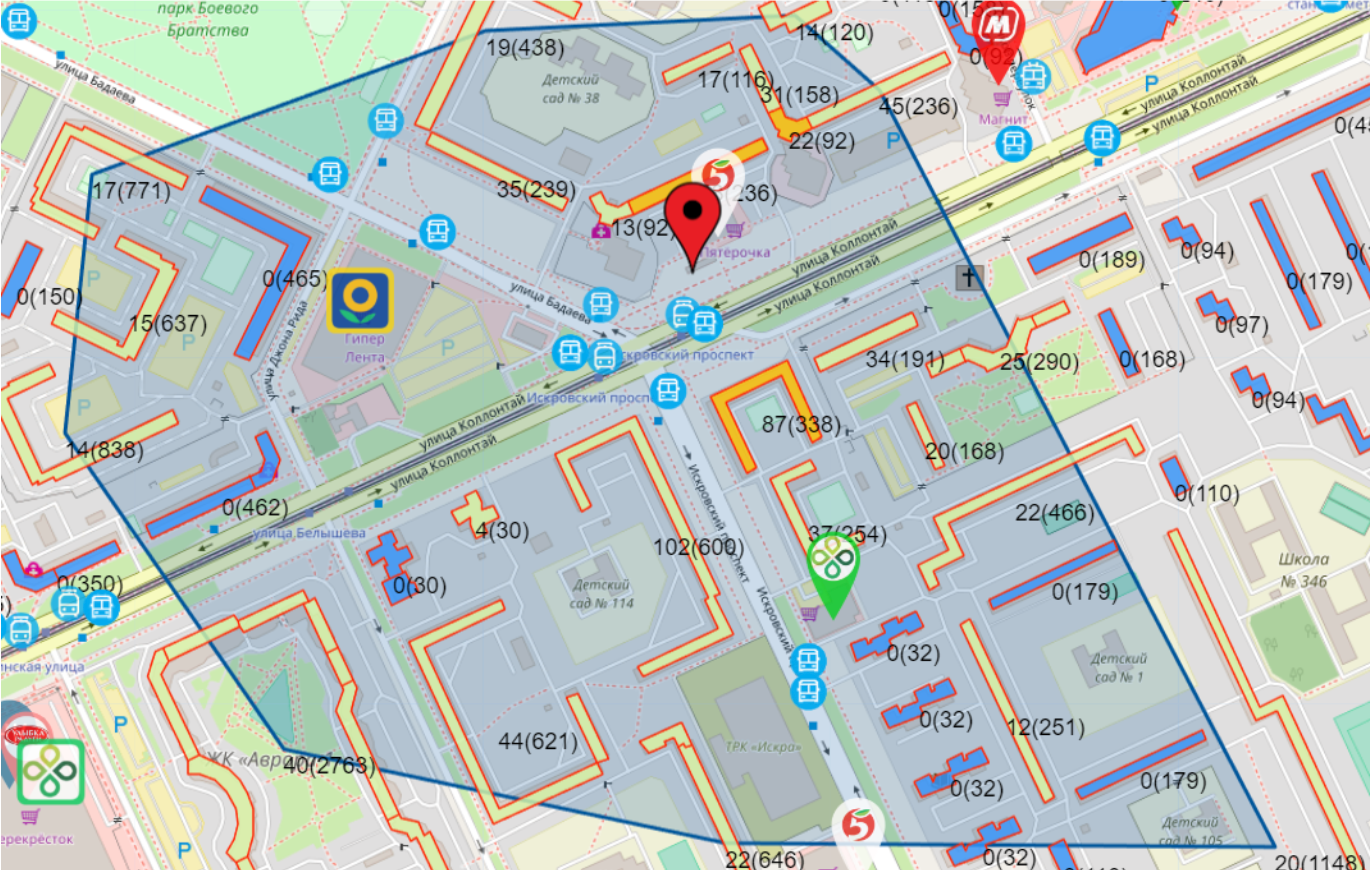
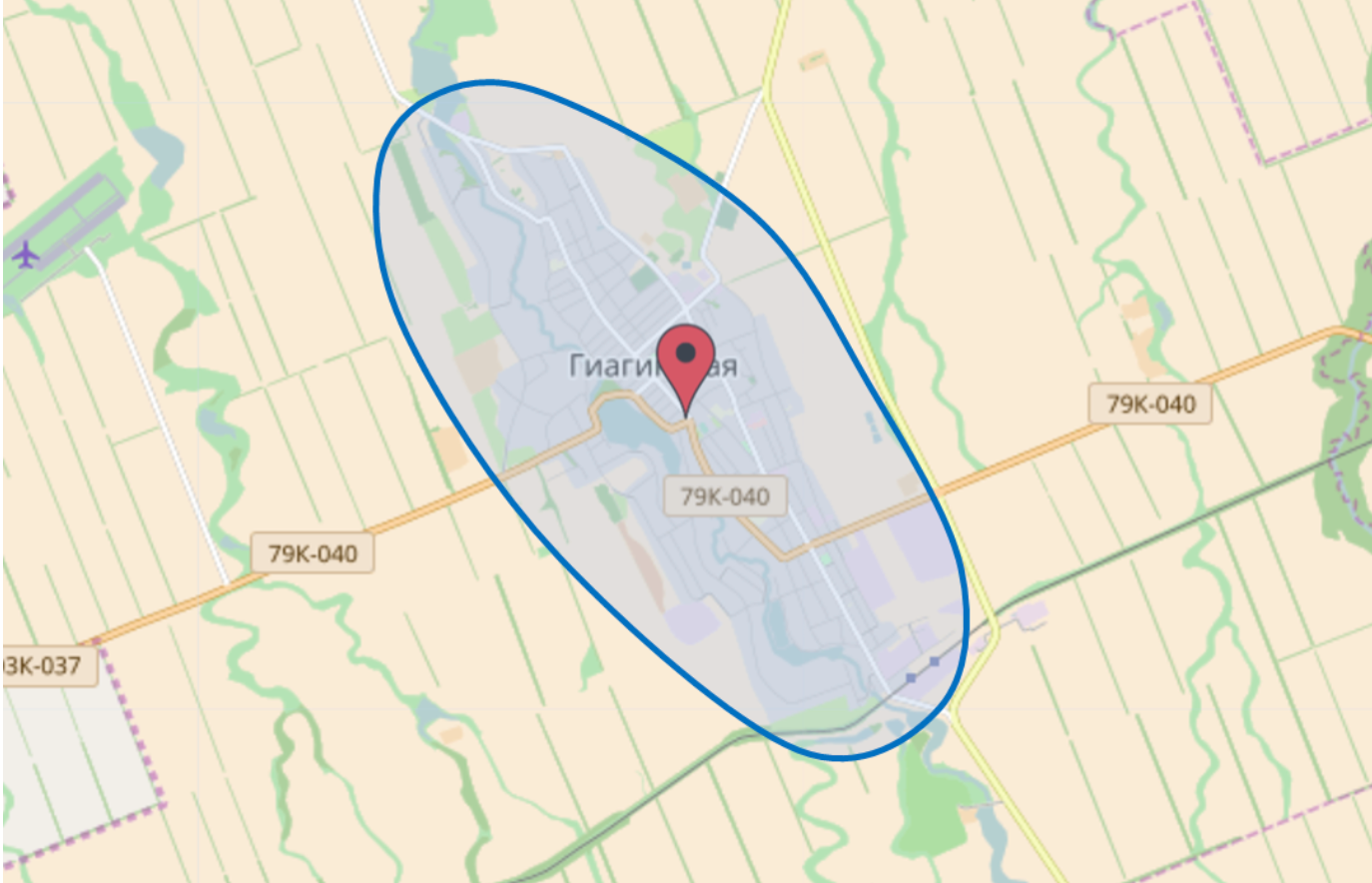
Сложности интерпретации результатов
Вероятностная природа показателя добавляет сложностей в процессе объяснения результатов расчётов, поэтому приходится использовать детерминистическую интерпретацию. То есть вместо фразы «каждая семья в доме с равной вероятностью может пойти в торговую точку 1 и в торговую точку 2» используется фраза «в торговую точку 1 идёт половина семей из дома, а другая половина идёт в торговую точку 2».
Удалённость двух конкурентов друг от друга оказывает различное влияние на привлечение покупателей из домов на близком и на дальнем расстоянии до торговых точек в силу нелинейного влияния расстояния в формуле. То есть существует такое расстояние, на котором удалённость двух конкурентов друг от друга будет для покупателя не так важна, как привлекательность торговой точки (логика «всё равно далеко ехать/идти»). Эта особенность модели становится проблемной при визуализации, так как рядовому пользователю непонятно, почему более крупная торговая точка при наличии конкурентов начинает привлекать больше покупателей из дальних домов, чем из ближних.
Где ещё используют балл Хаффа
Модель Хаффа используется в маркетинге, экономике, исследованиях розничной торговли и городском планировании и реализована в нескольких коммерчески доступных ГИС‑системах.
Применение модели можно встретить в нескольких направлениях:
В качестве признака в предиктивных моделях.
В нейронных сетях для оценки спутниковых снимков локаций.
В онлайн‑продажах (требуется корректировка параметров).
С развитием доставки в крупных городах требуется пересматривать классическую формулу балла Хаффа, так как расстояние до торговой точки перестаёт иметь значение для покупателя. Для корректного учёта такого вида торговых точек требуется пересмотреть логику определения привлекательности, убрав из неё локационную доступность и наличие поблизости точек интереса. Расстояние же от потенциального покупателя до торговой точки требуется заменять на некоторую константу, отражающую среднее время доставки.
Гравитационную модель Хаффа можно использовать в сочетании с учётом онлайн‑розницы, чтобы понять поведение потребителей и предсказать движение товаров как по онлайн, так и по офлайн каналам. Вот несколько способов его использования: многоканальная торговля, открытие потенциальных точек с учётом обоих каналов торговли конкурентов, управление запасами и маркетинг по обоим каналам торговли.
Заключение
Гравитационная модель Хаффа предлагает более детальное понимание распределения потенциальных покупателей между локациями и торговыми точками с разным уровнем привлекательности. Хотя это всё еще теоретическая модель, она с успехом применяется в наших предиктивных моделях в качестве признаков с высокой значимостью
Модель Хаффа — очень мощный инструмент генерации признаков для предиктивных моделей с использованием геоданных с очень высокой степенью применимости к различным сферам из‑за основополагающей идеи «гравитации» и вероятностной интерпретации результатов. С помощью этой абстракции можно распределять «по Хаффу» потенциальных покупателей, населённые пункты и любые другие физические объекты относительно друг друга.
Мы надеемся, что статья дала вам всестороннее понимание рассматриваемой темы. Ждём ваши отзывы и любые вопросы.
Кстати, обложка статьи создана с помощью ИИ. Да, она неидеальна, и внимательный читатель скорее всего заметил это. Но ИИ — новая данность современности, и наша статья — хорошее тому подтверждение.
Дополнительные материалы
Wesley Friske, Sunhee Choi. Another Look at Retail Gravitation Theory: History, Analysis, and Future Considerations. 2013
GISGeography.com. Huff Gravity Model: How Many Customers Will Visit Your Store?. 2022
Команда проекта
Михаил Большаков, владелец продукта.
Юрий Борисов, тимлид, автор статьи.
Дмитрий Молчанов, Дмитрий Машков, Дмитрий Сырчин, Виктор Сентено, Юрий Шевчук, Виталий Кузьмин — анализ и непосредственная реализация описанной модели.
Евгений Соловьев, Диана Барановская — экспертиза.
