Введение в математическую оптимизацию на примере компании Recruit. Часть 1

Что такое «математическая оптимизация» — четыре области применения, шаги по её применению к реальным проблемам, чем она отличается от машинного обучения и как её использовать иначе

Прим. переводчика: Ранее на хабре не было переводов статей с японского языка. Мы решили исправить это досадное упущение и начать переводить их ещё и с этого языка. Данный материал будет пробой пера.

Эта серия статей о том, что такое математическая оптимизация и как она может быть применена в бизнесе через представление примеров применения в компании Recruit. В первой статье представлен обзор математической оптимизации, четыре примера применения в Recruit, процедура применения к реальным случаям, отличия от машинного обучения и как использовать её иначе.

Другие части доступны здесь:

• Введение в математическую оптимизацию на примере компании Recruit. Часть 2
• Введение в математическую оптимизацию на примере компании Recruit. Часть 3

❖ автор Рёсуке Судо

В последние годы использование данных в бизнесе стало обычным делом для многих компаний. Многие читатели слышали об историях успеха, связанных, в частности, с использованием машинного обучения. С другой стороны, мало кто знает о реальности математической оптимизации — ещё одной техники использования данных, хотя она и достигает немалых результатов в различных областях.

Мы надеемся, что этот материал даст возможность читателям использовать математическую оптимизацию как один из методов использования данных.

Что такое математическая оптимизация?

Математическая оптимизация — это «метод определения проблемы реального мира в виде математического уравнения (математической модели) и нахождения значений переменных, которые минимизируют затраты или максимизируют прибыль при соблюдении ограничений». В данной оптимизации «целевая функция» — это числовое выражение затрат или прибыли, что является целью, которую необходимо минимизировать или максимизировать.

Чтобы применить математическую оптимизацию к реальной проблеме, сначала сформулируйте математическую модель «функции цели» и «ограничений» для реальной проблемы, которую необходимо оптимизировать. Затем выбирается алгоритм оптимизации, подходящий для решения математической модели, и рассчитываются значения переменных, которые максимизируют или минимизируют целевую функцию.

При математической оптимизации, сформулированный алгоритм может автоматически рассчитывать оптимальные значения переменных каждый раз, когда поступают новые данные. Поэтому он широко используется в бизнесе и обществе как метод автоматизации и поддержки принятия решений, которые раньше принимались человеком после того, как он каждый раз просматривал данные.

Поток математической оптимизации

Четыре примера применения математической оптимизации в Recruit

Чтобы дать вам конкретное представление о применении математической оптимизации в бизнесе, мы приведём несколько примеров использования оптимизации в Recruit. Подробности конкретных исследований будут представлены в более поздней серии статей, поэтому данная статья носит обобщённый характер.

▍ Оптимизация рекомендательных писем для пользователей

Recruit рассылает пользователям своих услуг материалы по электронной почте, информируя их о рекомендуемых продуктах и событиях.

Что касается содержания, то, хотя мы хотим рассылать электронные письма, представляющие наибольший интерес для каждого пользователя, нам необходимо придерживаться бизнес-ограничений, которые есть у каждой службы, например, максимальное количество писем, которые можно рассылать, и содержание, которое мы хотим сделать приоритетным на определённый период. По этой причине невозможно просто рассылать электронные письма с тем содержанием, которое кажется наиболее интересным каждому пользователю. Поэтому математическая оптимизация была использована для расчёта оптимального содержания для доставки по электронной почте и при соблюдении бизнес ограничений.

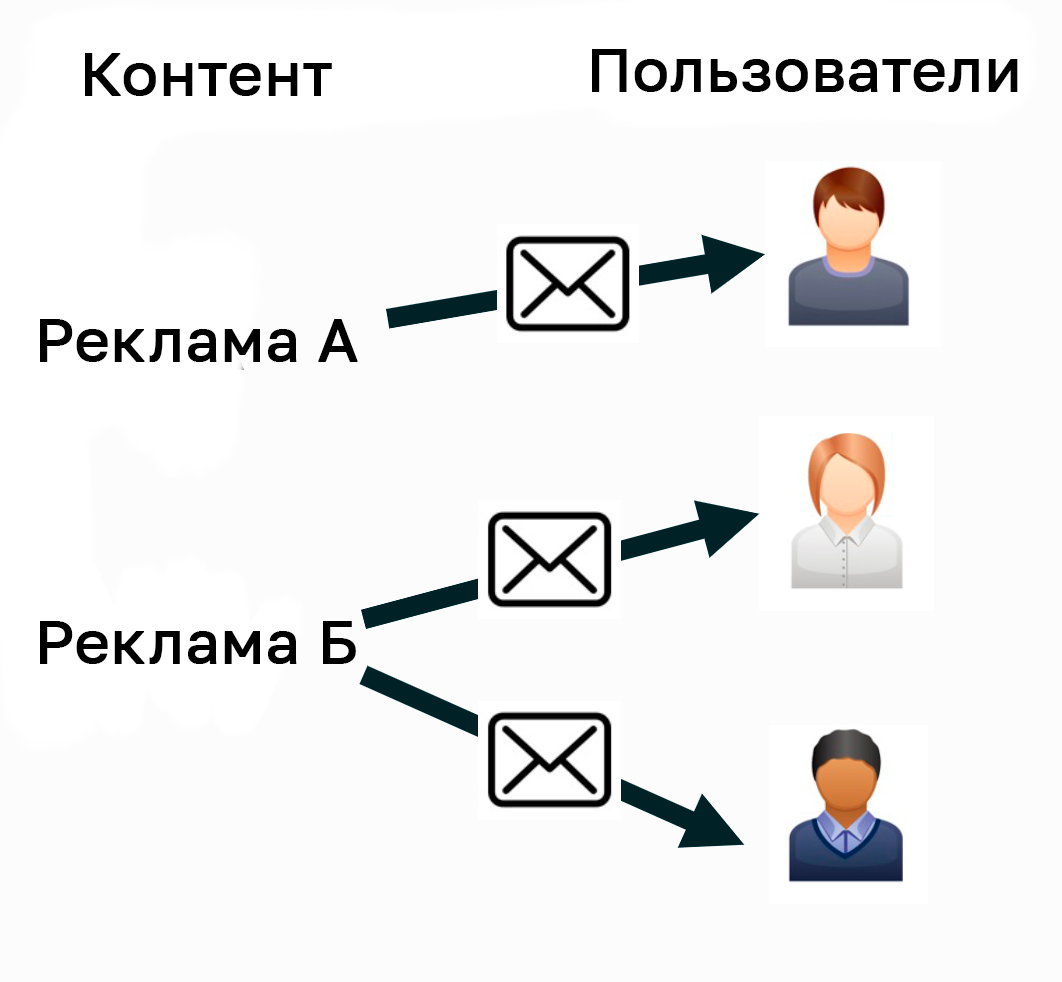
• Примеры того, что вы можете сделать: доставлять клиентам лучшие электронные письма, соблюдая при этом различные бизнес-ограничения (например, максимальное количество писем, приоритетные периоды рассылки и т.д.).
• Примеры переменных: тип писем, которые должны быть доставлены каждому пользователю, время доставки.
• Примеры целевых функций: максимизация коэффициента открытия электронной почты пользователями, максимизация количества клиентов, направленных на контент.
• Примеры ограничений: максимальное количество писем для определённого контента, приоритетный контент, который должен интенсивно доставляться в течение определённого периода времени.

▍ Оптимизация графика раздачи бесплатных газет

В каждом регионе у Recruit есть стойки, где они раздают бесплатные газеты. Поскольку несколько грузовиков должны посетить множество пунктов раздачи, важной проблемой является определение эффективного маршрута для объезда территории. Традиционно графики распределения грузовиков определялись вручную, но для решения этой проблемы был разработан эвристический решатель.

• Что вы можете сделать: определить оптимальное распределение грузовиков по стойкам и маршрутам доставки.
• Примеры переменных: распределение грузовиков по стойкам, маршруты доставки.
• Примеры целевых функций: топливо для грузовика, общее расстояние доставки, общее время доставки.
• Ограничения: доступные часы посещения, доступные часы работы на грузовик, ограничения по весу груза и т.д.

▍ Рекомендация оптимального порядка приготовления пищи на кухне

Одной из проблем в работе кухни ресторана являются задержки в подаче блюд. Для сокращения задержек в «Air Reg Order Kitchen Monitor» (продукт компании Recruit, позволяющий управлять заказами и приготовлением блюд в залах и кухнях ресторанов) предусмотрена функция, рекомендующая порядок приготовления блюд, при котором задержки могут быть сокращены с помощью математических оптимизационных задач. Кроме того, возможность сокращения задержек при обслуживании с помощью этой функции была проверена в демонстрационном эксперименте.

Прим. переводчика: большая часть блюд японской кухни имеет свои собственные названия и попытка их перевода на общее понимание не повлияет

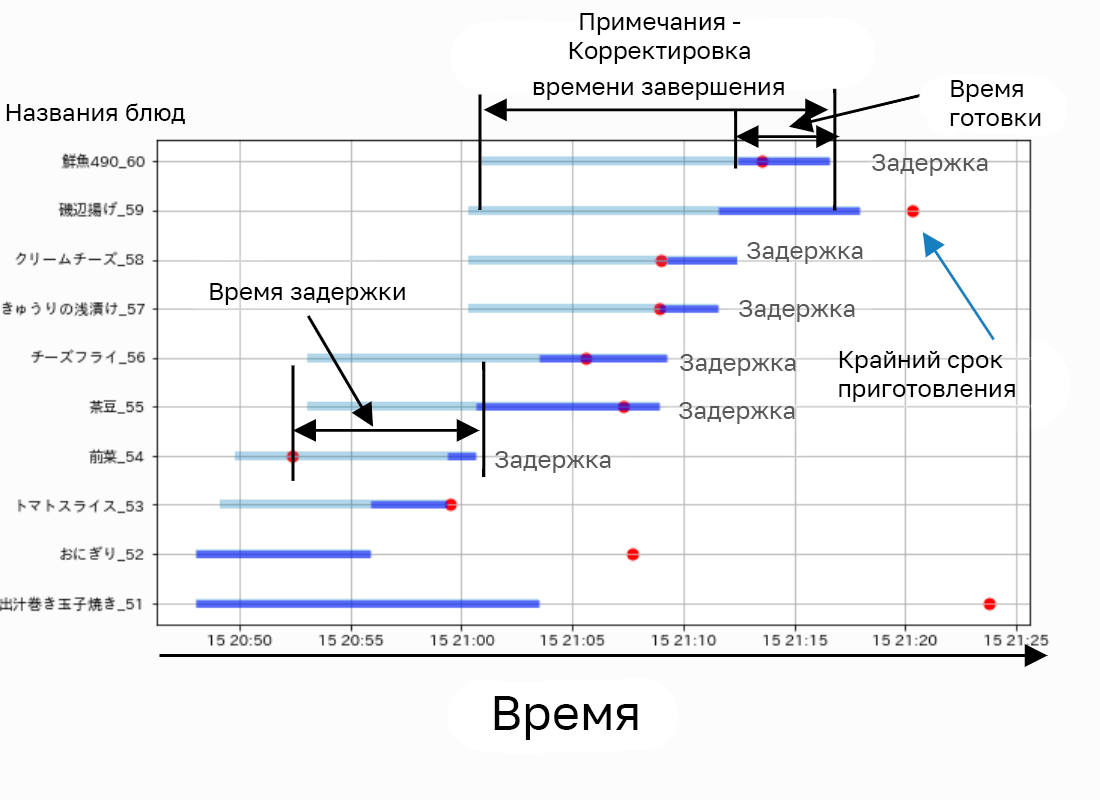
• Что мы можем сделать: рекомендовать лучший порядок приготовления пищи, который предпочитает пользователь на iPad.
• Примеры переменных: порядок приготовления, тип продукта, время приготовления.
• Примеры целевых функций: минимизация времени задержки приготовления, минимизация количества задержек приготовления.
• Примеры ограничений: количество одновременно работающих поваров, ограничения на порядок подачи, приоритет первого заказа.

▍ Оптимизация размещения в рекламных TV роликах

Компания Recruit использует телевизионные ролики в качестве одного из своих рекламных носителей. Хотя выбор того, какой коммерческий материал транслировать в ограниченном количестве рекламных слотов, оказывает значительное влияние на эффективность рекламы, процесс принятия решения является чрезвычайно сложным. Поэтому мы использовали математическую оптимизацию для расчёта того, «какой тип коммерческого сообщения должен быть выделен на тот или иной рекламный слот, представленный станцией, чтобы максимизировать рекламный эффект», и проверили в экспериментах, что можно достичь высокого рекламного эффекта.

• Что мы можем сделать: определить распределение рекламных материалов для достижения максимальной эффективности в ограниченном количестве рекламных слотов на телевидении.
• Пример переменной: распределение того, в каком слоте транслировать рекламный ролик.
• Пример целевой функции: максимизация количества распознанных зрителей.
• Примеры ограничений: количество рекламных роликов, которые могут транслироваться в тайм-слоте, минимальный GRP (Gross Rating Point: валовый рейтинг аудитории), выделенный на материал.

▍ Если вы хотите узнать больше об актуарной оптимизации в Recruit

Таким образом, Recruit использует математическую оптимизацию в самых разных областях, от рекомендаций до оптимизации размещения в телевизионной рекламе. Это показывает широкий спектр возможных применений математической оптимизации.

Если вы хотите узнать больше об опыте компании Recruit в области математической оптимизации, здесь также есть презентация Нишимуры из Recruit на японском языке, представляющий работу компании по использованию методов математической оптимизации.

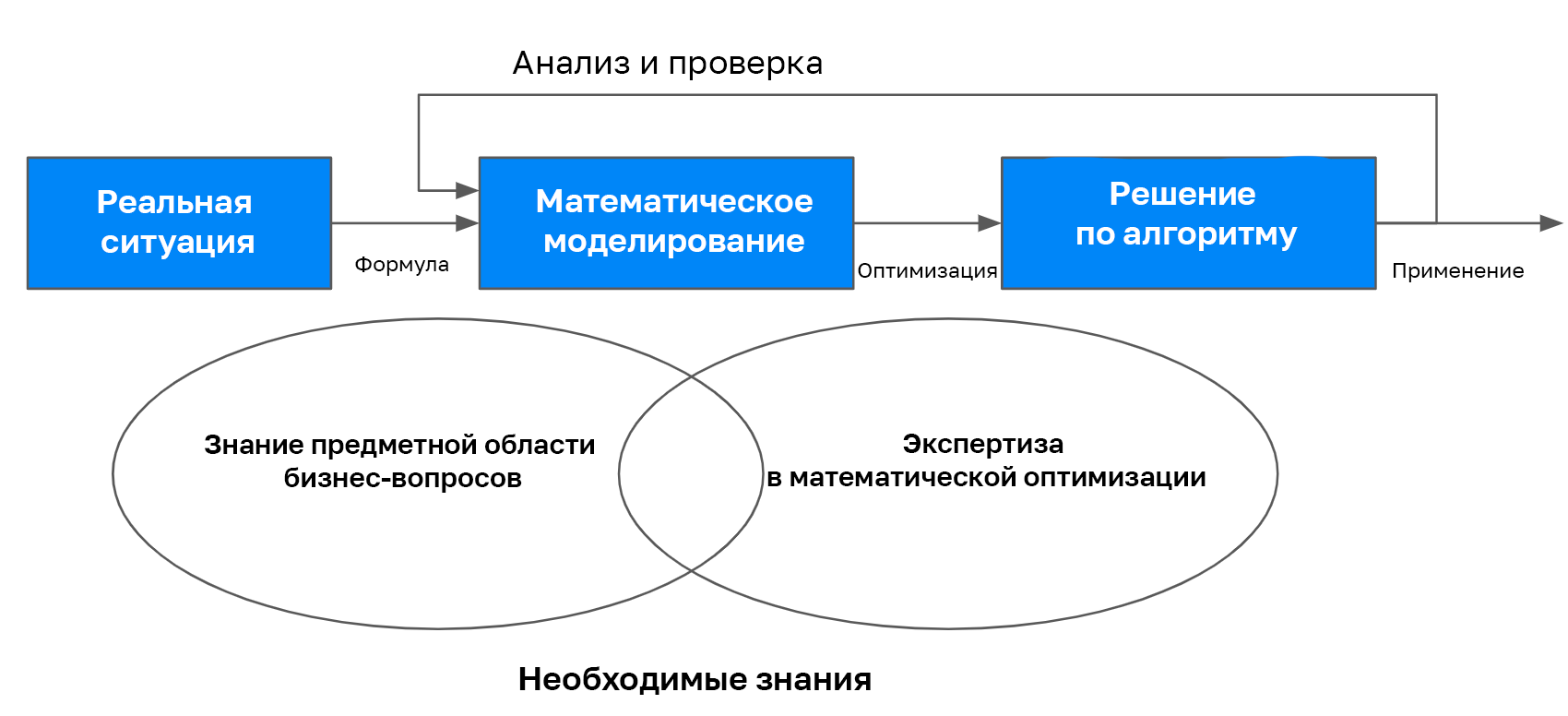
Процедуры применения математической оптимизации к реальным проблемам

В этом разделе описывается процедура применения математической оптимизации для решения бизнес-задач. Существует три основных этапа: 1. понимание бизнес-задачи, 2. построение математической модели и 3. алгоритмический поиск решений.

▍ 1. Понимание проблемы бизнеса

Первый шаг — подумать о том, какие ценности бизнес-задачи вы хотите решить, а какие — оптимизировать. Математическая оптимизация не является методом, определяющим понятие оптимального состояния, поэтому здесь необходимо мышление человека. Значение, которое вы хотите оптимизировать, должно быть определено как значение, которое, если его улучшить, позволит достичь бизнес-цели.

В некотором роде это похоже на определение KPI/KGI (Key Performance Indicators/Key Goal Indicators) в бизнесе. Естественно, требуются глубокие знания домена, и на этом этапе также необходимо организовать «при каких ограничениях вы хотите оптимизировать».

▍ 2. Математическое моделирование

Следующим шагом является выражение ограничений и оптимизируемого объекта в математических уравнениях (т.е. математическое моделирование), которые были изучены заранее. Недостаточно уметь сформулировать модель в произвольной форме, но в основном необходимо сформулировать модель в форме, которую легко решить в последующих алгоритмах, поэтому требуется определённая степень знания математического моделирования.

▍ 3. Алгоритмический поиск решения

Следующим шагом является реализация алгоритма для решения заданной математической модели и вычисления оптимального решения. В зависимости от предопределённой математической модели, может быть возможно вычислить оптимальное решение с помощью «универсального решателя» (универсальный решатель, который автоматически вычисляет оптимальное решение путём предоставления математической модели), без необходимости реализации нового оригинального алгоритма.

▍ Хоть суперталантов и не существует, но...

Таким образом, математическая оптимизация требует широкого спектра знаний — начиная с понимания бизнес-задачи и заканчивая реализацией алгоритмов. Однако существует очень мало людей, которые обладают всеми этими знаниями. Поэтому компания Recruit часто работает над проектами с командой из нескольких человек, например, используя сочетание ответственного сотрудника с сильными знаниями в бизнес-области и специалиста по исследованию данных с опытом в математической оптимизации.

Для того чтобы сделать задачу, необходимо найти область, где математическая оптимизация может оказать большое влияние на бизнес, поэтому необходимы специалисты широкого профиля, обладающие определёнными знаниями как в области бизнеса, так и в области оптимизации.

Процедуры и знания, необходимые для применения математической оптимизации для решения бизнес-задач

Чем оптимизация отличается от машинного обучения и как её использовать иначе

Частая тема разговора: «В чём разница между машинным обучением и математической оптимизацией?» является одной из самых распространённых тем.

Трудно провести строгое сравнение, поскольку они имеют широкие значения друг для друга, а в некоторых случаях используются в сочетании друг с другом, но следующие различия стоят сравнения в рамках правил пользования.

• Машинное обучение
  Методы, в которых модель неизвестна и интерес заключается в изучении (и использовании её для предсказания) закономерностей из данных (особенно «контролируемое обучение»).
• Математическая оптимизация
  Методы, в которых модель известна (или определена) и интерес заключается в том, чтобы вывести оптимальный выбор на основе заданных данных.

Учитывая эти особенности, можно провести различие между использованием машинного обучения в областях, где моделирование затруднено, и математической оптимизацией в областях, где моделирование возможно. Однако во многих деловых вопросах существует множество случаев, когда некоторые из них можно смоделировать, а некоторые — нет. По этой причине многие проекты, которые реализуются в Recruit, предполагают использование машинного обучения как части процесса математической оптимизации.

Например, в вышеупомянутой рекомендательной оптимизации доставки электронной почты в качестве параметра математической модели требуется показатель открытия электронной почты каждого пользователя. Однако эти значения невозможно получить напрямую, поэтому они прогнозируются с помощью машинного обучения и затем используются в качестве параметров для решения задачи оптимизации.

Машинное обучение и математическая оптимизация могут дополнять друг друга. Если вы относитесь к категории «я часто использую машинное обучение, но не так часто математическую оптимизацию......» или, наоборот, почему бы не узнать об обеих методиках?

Заключение

В этой первой статье цикла мы дали краткий обзор математической оптимизации и её применения в Recruit. Начиная со следующей статьи — мы представим конкретные примеры, так что если вы думаете: «Этого недостаточно!», я буду рад, если вы прочтёте также следующую и последующие статьи после их выхода.