Перевод поста Стивена Вольфрама (Stephen Wolfram) "Pi or Pie?! Celebrating Pi Day of the Century (And How to Get Your Very Own Piece of Pi)"
Выражаю огромную благодарность тем, кто помог мне сделать этот перевод: Курбану Магомедову и Ольге Лавренюк.
Эта суббота будет «Днем числа Пи» века. Дата 3/14/15 в формате месяц/день/год задает первые цифры числа π=3.1415… А 9:26:53.589… утра будет «супер моментом дня числа Пи».
Благодаря Mathematica и Wolfram|Alpha, я уверен, что наша компания выдала миру больше раз число π, чем какая-либо другая организация в истории. Поэтому, конечно, мы должны сделать нечно особенное (мероприятие SXSW) для этого особенного Дня числа Пи.
Корпоративная путаница
Одна из моих задач как CEO — придумывать идеи и я провел десятилетия строя организацию, которая хорошо воплощала бы их в жизнь. Так, несколько недель назад я присутствовал на встрече посвященной грядущим корпоративным событиям и кто-то заметил, что День числа Пи (3/14) будет происходить во время большого ежегодного фестиваля SXSW (South by Southwest) в Остине (штат Техас). Я сказал (ну или по крайней мере я подумал, что сказал это), «We should have a big pi to celebrate Pi Day» <используется непереводимая игра слов pi — pie (пирог), которая важна в дальнейшем>.
Я больше не думал над этим, но спустя пару недель у нас было другое совещание о текущих делах компании. Одним из пунктов на повестке дня был как раз День Пи. Человек, который ведет нашу группу, ответственную за всевозможные мероприятия, начал говорить о том, что будет трудно найти в Остине пекарню, которая сделала бы достаточно большой пирог. Я воскликнул «О чем ты говоришь?» и затем добавил «Ты понял совсем не так то, что я имел ввиду!».
Я думаю, что в нашем <англоязычном> мире проблема <того, что понимается под> Пи очень обычна. Система распознавания речи в Siri посылает в Wolfram|Alpha множество запросов о «пирогах» (pie), которые мы должны интерпретировать как число Пи (pi). Также есть и одноплатный компьютер Raspberry Pi, на котором предустановлен язык Wolfram Language. В мою же жизнь вносит еще больше путаницы то, что мой персональный файловый сервер много лет носил название “pi”.
После этой ошибки pi(e) мы продолжили совещание и придумали множество идей о том, как отпраздновать День Пи. Мы уже арендовали небольшую площадку на территории фестиваля SXSW и нам захотелось сделать самый интересный «обратный отсчет до Дня Пи», который только можно. Мы решили сделать большое количество съедобных «пиксельных» тортиков, которые будут объединены в форме числа Пи в один большой торт. Конечно, там будет и специальная площадка для Пи-селфи в виде «Стоунхенджеподобного» числа Пи, а также торт декорированный с помощью числа Пи в виде Wolfie <логотип Wolfram Language> для дополнительных селфи. Ну и конечно же мы будем делать разные вещи и на Raspberry Pi.
Частичка числа Пи для каждого
Я уверен, что на фестивале SXSW все мы получим много «пи-удовольствия». Но мы также хотим, чтобы все желающие во всем мире могли принять участие в праздновании Дня числа Пи. Нас мучал вопрос «Что кто-то мог бы сделать с числом пи?». На самом деле, в некотором смысле, каждый может делать с числом Пи что угодно. Скажем, помимо того, что число Пи имеет бесконечно много знаков в своей записи, их бесконечная последовательность, в целом, полностью случайна. Так, например, в ней встретится любая наперед заданная последовательность цифр.
Как насчет того, чтобы дать людям личную связь с этой частью математики? День числа Пи происходит в день, который соответствует первым цифрам числа Пи. Но любая дата присутствует где-то в записи числа Пи. Итак, мы подумали: «Почему бы не дать людям возможность найти место, где в записи числа Пи встречается их день рождения (или любая другая дата) и затем создать, скажем, персонализированные пи-футболки и пи-постеры?»
В языке Wolfram Language очень легко найти позицию, которую «занимает» ваш день рождения в числе π. В целом, любая дата в формате мм/дд/гг встретится среди первых 10 миллионов знаков числа Пи. На моем настольном компьютере (Mac Pro) вычисление этих 10 млн. знаков числа Пи заняло 6.28 с (2π?!)
Ниже представлен код на языке Wolfram Language, который позволяет получить этот результат и представить его в виде строки (отбросив разделить целой и дробной части, находящийся на втором месте в полученной строке):
Теперь легко найти любую «строку-день рождения»
Так, например, мое день рождения встречается впервые в записи числа π начиная с цифры под номером 151 653.
Как наглядно отобразить это? Это зависит от того, насколько «пи-удачливым» вы оказались. Скажем, для тех, кто родился 4/15/92, их день рождения встречается уже на позиции 3. Люди, родившиеся 23 ноября 1960 г. имеют «строку-день рождения», которая начинается лишь начиная с 9 982 546 знака числа Пи. При этом, на самом деле, большинство людей имеют дни рождения, которые находятся «довольно далеко» в записи числа π (в среднем, это позиции около 306 150).
У нашего главного художника, который работает у нас уже очень долго, появилась идея использовать спираль, которая закручивается сначала внутрь, а затем наружу, для того, чтобы отобразить начало и конец таких длинных последовательностей цифр. И почти сразу же он написал код, который ее создает (одной из самых потрясающих вещей в языке Wolfram Language заключается в том, что даже люди без технического образования могут легко писать свой собственный код...).
Затем он развернул свой код в Интернете. Благодаря Wolfram Programming Cloud, это было сделано по сути всего лишь в одну строку кода. Теперь, вы можете перейти на этот сайт MyPiDay.com…
…и получить свою собственную частичку числа пи!
После чего вы можете поделиться полученным изображением или же заказать футболку с ним:
Наука о числе Пи
Хотя мы и много уже говори о числе Пи, я не могу устоять перед тем, чтобы рассказать немного о числе Пи с научной точки зрения. Но, для начала, ответим на вопрос: почему число Пи так известно? Да, это отношение длины окружности к ее диаметру. И это уже само по себе означает, что число Пи встречается в миллиардах научных формул. Но это не все. (Скажем, например, большинство людей никогда не слышало о аналоге числа π для эллипса — о так называемом полном эллиптическом интеграле второго рода).
Интереснее то, что число π встречается в значительном количестве математических конструкций — включая множество таких, которые, вроде бы, не имеют ничего общего с окружностями. Такие как, скажем, суммы отрицательных степеней или пределы некоторых последовательностей, или же вероятность того, что случайно выбранная дробь будет несократимой.
Если просто взглянуть на последовательность цифр числа Пи 3.1415926...., то на первый взгляд в ней нет ничего особенного. Но, допустим, мы начнем создавать формулы случайным образом и затем будем производить традиционные математические операции над ними, такие как, скажем, суммирование рядов, поиск интегралов, пределов и т.п. Мы получим очень много ответов вида 0 или 1/2 или
. Но при этом также будет и много случаев, когда мы не сможем найти результат в некоторой замкнутой форме, а только лишь численно. Но в тех случаях, когда он может быть получен, мой опыт говорит мне, что очень часто в нем будет содержаться число π.Несколько других констант также будет появляться часто, скажем — число e (2.1718…), постоянная Эйлера — Маскерони (0.5772…) или постоянная Каталана (0.9159…). Но число π появляется явно чаще.
Возможно, математика могла бы иметь и другой вид. Но, по крайней мере с математикой которую создали мы, люди, число π является очень распространенным строительным кирпичиком, и вполне естественно, что мы дали ему имя и что оно стало известно настолько, что мы выделили для празднования этого числа отдельный день.
Что можно сказать о других константах? «Строки дней рождения» будут, конечно же, встречаться в различных позициях различных констант. И, подобно тому, как сервис Wolfram|Alpha пытается найти замкнутую форму для некоторой десятичной дроби, так же можно найти положение некоторой последовательности цифр внутри других констант. Так, например, мой день рождения встречается на позиции 151 653 в числе π, 241 683 в числе e, 45 515 в
, 40 979 в ζ(3) … и 196 в 1601-м числе Фибоначчи.Случайность в числе π
Давайте, скажем, построим график функции, которая возрастает всякий раз, когда цифра числа π больше или равна пяти и убывает в противном случае:
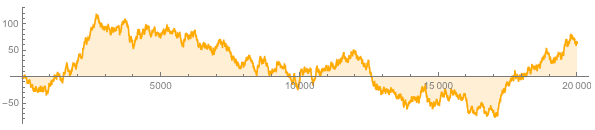
График выглядит как случайное блуждание. При этом, все статистические и криптографические тесты на случайность, которые проводились над цифрами числа Пи (исключая тесты, которые просто спрашивают «а не цифры ли это из числа пи?») подтверждают это предположение.
Почему же так происходит? Существуют простые процедуры, которые генерируют цифры числа Пи. Но поразительно то, что даже несмотря на то, что эти процедуры просты, результат их выполнения сложный до такой степени, чтобы казаться полностью случайным. В прошлом не возникало обстоятельств, при которых люди рассуждали бы о таком поведении. Но именно на изучение подобного рода систем я потратил много лет и написал книгу A New Kind of Science (Новый вид науки). В некотором смысле тот факт, что любой человек может найти свой день рождения в записи числа Пи непосредственно связан с концепциями, такими как, скажем, "Принцип вычислительной эквивалентности", который я выдвинул в своей книге.
SETI и цифры числа пи
Конечно, только потому, что мы никогда не видели какую-либо закономерность в цифрах числа Пи, это еще не означает, что такой закономерности не существует. В самом деле — всё ещё возможно, что если бы мы сделали достаточно большой поиск, мы могли бы найти где-то далеко в цифрах числа Пи какую-то, скрывающуюся, странную закономерность.
Что бы это означало? Существует ответ из области научной фантастики, приведенный в конце книжной версии "Контакта" Карла Сагана. В книге, поиск внеземного разума заканчивается установлением контакта с межзвездной цивилизацией, которая создала удивительные артефакты — после этого объясняется, что самое важное, что было обнаружено, закодировано как раз в далеких цифрах числа Пи, в которых они нашли разумные послания, такие как, скажем, закодированное изображение окружности.
Вначале можно подумать, что поиск «разума» в цифрах числа Пи — абсурд. Ведь, в конце концов, существует вполне определенный простой алгоритм, который генерирует эти цифры. Но если мои подозрения на этот счет верны также, как и подозрения насчет всей нашей Вселенной, то на самом деле каждая деталь ее истории, в принципе, вычислима так же, как цифры числа Пи.
Теперь мы знаем, что в нашей Вселенной мы сами выступаем в качестве примера разума. SETI (Search for Extraterrestrial Intelligence) просто пытается найти другие примеры. Эта задача достаточно хорошо определяется в случае, если мы ищем «разум человеческого типа». Но, в соответствии с тем, что предполагает мой Принцип вычислительной эквивалентности, я думаю, что в целом практически невозможно сделать точное различие между тем, что следует считать «разумным» и тем, что считается «просто вычислимым».
Если вековые математические подозрения относительно того, что цифры числа Пи «нормальны» верны, то это будет автоматически означать, что любая последовательность цифр обязательно встретится рано или поздно среди цифр числа Пи, включая все работы Шекспира, или любое другое наследие любой возможной цивилизации. Но может ли быть какая-либо другая структура — возможно даже накладывающаяся на нормальность — которая, к примеру, может служить доказательством появления «разумной» сложности?
Хотя она может быть концептуально простой, конечно же кажется намного более странным искать возможность существования разумной человекоподобной цивилизации в цифрах числа Пи, чем в физической Вселенной, наблюдаемой SETI. Но если мы обобщим то, что мы рассматриваем в качестве разумного, ситуация становится намного менее очевидной.
Конечно, если мы наблюдаем сложный сигнал из магнитосферы пульсара мы скажем, что это «просто физика», а не результат эволюции «магнетогидродинамической цивилизации». Подобно этому, если мы наблюдаем некоторую сложную структуру в цифрах числа Пи, мы говорим что это «просто математика», а не результат жизни некоторой “теоретико-числовой цивилизации”.
Мы можем перейти от последовательности цифр числа Пи к представлениям любой математической константы, которые легко задать с помощью традиционных математических операций. В некоторых случаях существуют определенные закономерности в таких представлениях. Но часто все выглядит опять таки случайно. И проект поиска структуры в таких случаях в целом аналогичен проекту SETI в физической Вселенной. (Одно из различий, однако, заключается в том, что число π, как объект для изучения, выбрано нами в результате структуры нашей физической Вселенной, нашего мозга и нашего математического развития. Вселенная сама по себе, вероятно, не имеет возможности сделать подобный выбор, который дан нам неявно ввиду того, что мы существуем в ней.)
Я провел много времени в поиске закономерностей в представлении чисел, таких как Пи. Я не нашел ничего существенного. Думаю излишне говорить, что какие-либо закономерности вообще легко найти. И существует вероятность того, что потребуются усилия, столь же большие, как и в проекте SETI, чтобы их обнаружить.
Но сейчас, давайте праздновать День числа Пи нашего века и получать удовольствие от таких вещей, как поиск «строк дней рождения» в записи числа пи. Конечно, кто-то, как и я, может лишь надеяться на то, что к следующему Дню числа Пи века, который состоится в 2115 г., мы добьемся успеха в проекте SETI или “SETI среди цифр”…
Ресурсы для изучения Wolfram Language (Mathematica) на русском языке: habrahabr.ru/post/244451
