273.48
Общий рейтинг
Алгоритмы *
Все об алгоритмах
Сначала показывать
Порог рейтинга
Уровень сложности
ШишНашКи
2 мин
18K
Что тут? Математическая головоломка, немножко групповых перестановок, две задачи для узколобых и грань шутки. Beg your pardon, если эта головоломка придумана до меня и я жалкий невежа, вообразивший, что изобрел нечто новенькое. В случае лицензионной чистоты я нарекаю её ШишНашКи отныне и вовеки веков. Аминь.
По следам публикации
Человеческий гений в лице Mrrl решил задачу Бога в уме за 20 ходов.
Видео решения
+9
Курс по машинному обучению на Coursera от Яндекса и ВШЭ
4 мин
120KКогда-то мы публиковали на Хабре курс по машинному обучению от Константина Воронцова из Школы анализа данных. Нам тогда предлагали сделать из этого полноценный курс с домашними заданиями и разместить его на Курсере.
И сегодня мы хотим сказать, что наконец можем выполнить все эти пожелания. В январе на Курсере пройдёт курс, организованный совместно Яндексом (Школой анализа данных) и ВШЭ. Записаться на него можно уже сейчас: www.coursera.org/learn/introduction-machine-learning.

Сооснователь Coursera Дафна Коллер в офисе Яндекса
Курс продлится семь недель. Это означает, что по сравнению с ШАДовским двухсеместровым курсом он будет заметно упрощен. Однако в эти семь недель мы попытались вместить только то, что точно пригодится на практике, и какие-то базовые вещи, которые нельзя не знать. В итоге получился идеальный русскоязычный курс для первого знакомства с машинным обучением.
Кроме того, мы верим, что после прохождения курса у человека должна остаться не только теория в голове, но и скилл «в пальцах». Поэтому все практические задания построены вокруг использования библиотеки scikit-learn (Python). Получается, что после прохождения нашего курса человек сможет сам решать задачи анализа данных, и ему будет проще развиваться дальше.
Под катом можно прочитать подробнее обо всех авторах курса и узнать его примерное содержание.
И сегодня мы хотим сказать, что наконец можем выполнить все эти пожелания. В январе на Курсере пройдёт курс, организованный совместно Яндексом (Школой анализа данных) и ВШЭ. Записаться на него можно уже сейчас: www.coursera.org/learn/introduction-machine-learning.

Сооснователь Coursera Дафна Коллер в офисе Яндекса
Курс продлится семь недель. Это означает, что по сравнению с ШАДовским двухсеместровым курсом он будет заметно упрощен. Однако в эти семь недель мы попытались вместить только то, что точно пригодится на практике, и какие-то базовые вещи, которые нельзя не знать. В итоге получился идеальный русскоязычный курс для первого знакомства с машинным обучением.
Кроме того, мы верим, что после прохождения курса у человека должна остаться не только теория в голове, но и скилл «в пальцах». Поэтому все практические задания построены вокруг использования библиотеки scikit-learn (Python). Получается, что после прохождения нашего курса человек сможет сам решать задачи анализа данных, и ему будет проще развиваться дальше.
Под катом можно прочитать подробнее обо всех авторах курса и узнать его примерное содержание.
+78
Совмещенный АВС и XYZ анализ в Ритейле
7 мин
52KКогда-то давно владелец магазина, он же продавец, мог легко запомнить все товары своего ассортимента. Рассказать об особенностях каждого, историю, насколько товар эффективен, знал точно как он продается, когда заказать еще…
С развитием ритейла управление движением товаров требует других подходов. Системы учета и аналитики продаж, управления ассортиментом дополняют опыт работников магазина или торговой сети.
Серьезные решения, например, о выведении товара из ассортимента, принимаются не так просто. И категорийному менеджеру, и управляющему магазином нужны обоснования для таких действий.
Поэтому одного вида анализа недостаточно. Применяют совмещение нескольких видов (по-другому, кросс-анализ).
В статье мы на примере товарной группы “Кондитерских изделий” рассмотрим основные подходы к организации кросс-анализа. А еще узнаем, кто виноват в том, что Рафаэлло — товар с нестабильными продажами.

С развитием ритейла управление движением товаров требует других подходов. Системы учета и аналитики продаж, управления ассортиментом дополняют опыт работников магазина или торговой сети.
Серьезные решения, например, о выведении товара из ассортимента, принимаются не так просто. И категорийному менеджеру, и управляющему магазином нужны обоснования для таких действий.
Поэтому одного вида анализа недостаточно. Применяют совмещение нескольких видов (по-другому, кросс-анализ).
В статье мы на примере товарной группы “Кондитерских изделий” рассмотрим основные подходы к организации кросс-анализа. А еще узнаем, кто виноват в том, что Рафаэлло — товар с нестабильными продажами.

+13
Легендарные книги Амазона. Продолжение темы «Elements of Programming Interviews: The Insiders' Guide»
1 мин
9.8KДобрый день, Хабр!
В начале лета мы уже говорили об одной из легенд Амазона «Elements of Programming Interviews: The Insiders' Guide».
 Книга продолжает занимать первые места в рейтинге Амазона, но в сентябре 2015 года авторы выпустили еще одну книгу, которая тоже сразу стала бестселлером.
Книга продолжает занимать первые места в рейтинге Амазона, но в сентябре 2015 года авторы выпустили еще одну книгу, которая тоже сразу стала бестселлером.
Elements of Programming Interviews in Java: The Insiders' Guide
В начале лета мы уже говорили об одной из легенд Амазона «Elements of Programming Interviews: The Insiders' Guide».
 Книга продолжает занимать первые места в рейтинге Амазона, но в сентябре 2015 года авторы выпустили еще одну книгу, которая тоже сразу стала бестселлером.
Книга продолжает занимать первые места в рейтинге Амазона, но в сентябре 2015 года авторы выпустили еще одну книгу, которая тоже сразу стала бестселлером. Elements of Programming Interviews in Java: The Insiders' Guide
+6
Алгоритмы: теория и практика. Методы
2 мин
35KТуториал
В ноябре мы запускаем онлайн-курс «Алгоритмы: теория и практика. Методы» от Computer Science центра. Курс бесплатный, приглашаются все желающие. В курсе будут подробно разобраны базовые алгоритмические методы: жадные алгоритмы, метод «разделяй и властвуй», динамическое программирование. Для всех алгоритмов будут математически строго доказаны корректность и оценки на время работы. Мы постарались изложить материал так, чтобы были понятны и сами алгоритмы, и то, как можно было бы догадаться до их основных идей. Помимо теоретических основ, будут рассказаны тонкости реализации алгоритмов на языках программирования C++, Java и Python. В частности, будет рассказано, какие есть общие практики написания кода, позволяющие минимизировать вероятность ошибки, как писать и тестировать код, где стоит использовать стандартные методы, а не изобретать колесо.
Мы тщательно подобрали задачи для закрепления материала. Большинство алгоритмов, которые вы узнаете, вам нужно будет запрограммировать. Это лучший способ убедиться, что вы разобрались во всех деталях. Решая такие задачи, вы получите ценный опыт написания и отладки эффективных и надёжных программ. Задачи на программирование помогут вам почувствовать разницу между плохим (медленным) и хорошим (быстрым) алгоритмом. Вас также ждут тесты (где нужно выбрать правильные ответы из предложенных) и теоретические задачи (в них нужно доказать математическое утверждение). Наконец, в курсе есть также задачи повышенной сложности — менее стандартные задачи, которые не являются обязательными для прохождения курса. Получить удовольствие от решения этих задач смогут и те, кто уже знаком с базовыми алгоритмами.
+25
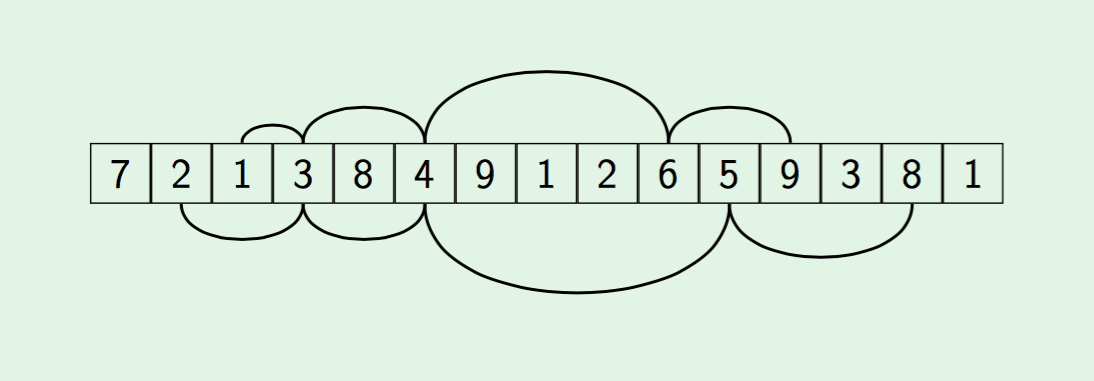
Непересекающиеся множества и загадочная функция Аккермана
14 мин
41KТуториал
 Речь пойдёт о простой структуре данных — системе непересекающихся множеств. Вкратце: даны непересекающиеся множества (например, компоненты связности графа) и по двум элементам x и y можно: 1) узнать, находятся ли x и y в одном множестве; 2) объединить множества, содержащие x и y. Сама структура очень проста в реализации и описывалась много раз в различных местах (например, есть хорошая статья на хабре и ещё кое-где). Но это один из тех удивительных алгоритмов, написать который ничего не стоит, а вот разобраться, почему он работает эффективно совсем нелегко. Я постараюсь изложить относительно простое доказательство точной оценки на время работы этой структуры данных, придуманное Зейделем и Шариром в 2005 (оно отличается от того ужаса, который многие могли видеть в других местах). Конечно, сама структура тоже будет описана, а попутно разберёмся причём здесь обратная функция Аккермана, о которой многие знают только, что она оооочень медленно растёт.
Речь пойдёт о простой структуре данных — системе непересекающихся множеств. Вкратце: даны непересекающиеся множества (например, компоненты связности графа) и по двум элементам x и y можно: 1) узнать, находятся ли x и y в одном множестве; 2) объединить множества, содержащие x и y. Сама структура очень проста в реализации и описывалась много раз в различных местах (например, есть хорошая статья на хабре и ещё кое-где). Но это один из тех удивительных алгоритмов, написать который ничего не стоит, а вот разобраться, почему он работает эффективно совсем нелегко. Я постараюсь изложить относительно простое доказательство точной оценки на время работы этой структуры данных, придуманное Зейделем и Шариром в 2005 (оно отличается от того ужаса, который многие могли видеть в других местах). Конечно, сама структура тоже будет описана, а попутно разберёмся причём здесь обратная функция Аккермана, о которой многие знают только, что она оооочень медленно растёт. +38
Машинное обучение, предсказание будущего и анализ причин успеха в электронной коммерции
10 мин
28K
Мы продолжаем публиковать материалы с летней конференции Bitrix Summer Fest. На этот раз хотим поделиться выступлением Александра Сербула, посвящённым текущим трендам в сфере машинного обучения, доступным методикам, а также практическим способам использования математики для увеличения конверсии и удержания клиентов.
Материал ни в коем случае не претендует быть формальным и научно строгим. Воспринимайте его как лёгкое, весёлое, полезное и ознакомительное «чтиво».
+20
Освоение специальности Data Science на Coursera: личный опыт (ч.2)
8 мин
29K
Мы публикуем вторую часть поста Владимира Подольского vpodolskiy, аналитика в департаменте по работе с образованием IBS, который закончил обучение по специализации Data Science на Coursera. Это набор из 9 курсеровских курсов от Университета Джонса Хопкинса + дипломная работа, успешное завершение которых дает право на сертификат.
Читайте в первой части: О специальности Data Science в общих чертах. Курсы: Инструменты анализа данных (программирование на R); Предварительная обработка данных; Документирование процесса обработки данных.
Часть 2
+11
Задача Александра Ивановича Корейко
7 мин
14KАлександр Иванович Корейко, один из ничтожнейших служащих ГЕРКУЛЕС’а, был человек в последнем приступе молодости, ему было 38 лет. На красном сургучном лице сидели желтые пшеничные брови и белые глаза. Английские усики цветом даже походили на созревший злак. Лицо его казалось бы совсем молодым, если бы не грубые ефрейторские складки, пересекавшие щеки и шею. На службе Александр Иванович вел себя как сверхсрочный солдат: не рассуждал, был исполнителен, трудолюбив, искателен и туповат.
— Робкий он какой-то, — говорил о нем начальник финсчета, — какой-то уж слишком приниженный, преданный какой-то чересчур. Только объявят подписку на заем, как он уже лезет со своим месячным окладом. Первым подписывается. А весь оклад-то 46 рублей. Хотел бы я знать, как он существует на эти деньги.
Была у Александра Ивановича удивительная особенность. Он мгновенно умножал и делил в уме большие трехзначные и четырехзначные числа. Но это не освободило Александра Ивановича от репутации туповатого парня.
— Слушай, Александр Иванович, — спрашивал сосед, — сколько будет 836 на 423?
(«Золотой теленок», Илья Ильф, Евгений Петров )
-6
Back to the Code – отчёт о состязании
2 мин
11KПеревод

Состязание под названием «Back to the Code» отметило наш возврат к многопользовательским играм. Миссия игры состояла в том, чтобы помочь Доку и Марти заполучить Альманах до того, как на него наложит свои лапы Биф Таннен. Для достижения цели у них было одно секретное оружие: трюк с помощью которого они могли вовращаться в прошлое и менять ход вещей… к лучшему или к худшему.
+14
SpecFlow и альтернативный подход к тестированию
11 мин
33K Тестирование с помощью SpecFlow прочно вошло в мою жизнь, в список необходимых технологий для «хорошего проекта». Более того, несмотря на ориентированность SpecFlow на behaviour тесты, я пришел к мысли, что и integration и даже unit тесты могут получить преимущества этого подхода. Конечно, в написании таких тестов уже не будут участвовать люди из BA и QA, а только сами разработчики. Разумеется, что для небольших тестов это привносит немалый оверхэд. Но насколько же приятнее читать человеческое описание теста, нежели голый код.
Тестирование с помощью SpecFlow прочно вошло в мою жизнь, в список необходимых технологий для «хорошего проекта». Более того, несмотря на ориентированность SpecFlow на behaviour тесты, я пришел к мысли, что и integration и даже unit тесты могут получить преимущества этого подхода. Конечно, в написании таких тестов уже не будут участвовать люди из BA и QA, а только сами разработчики. Разумеется, что для небольших тестов это привносит немалый оверхэд. Но насколько же приятнее читать человеческое описание теста, нежели голый код.+3
Освоение специальности Data Science на Coursera: личный опыт (ч.1)
9 мин
73K
Недавно Владимир Подольский vpodolskiy, аналитик в департаменте по работе с образованием IBS, закончил обучение по специализации Data Science на Coursera. Это набор из 9 курсеровских курсов от Университета Джонса Хопкинса + дипломная работа, успешное завершение которых дает право на сертификат. Для нашего блога на Хабре он написал подробный пост о своей учебе. Для удобства мы разбили его на 2 части. Добавим, что Владимир стал еще и редактором проекта по переводу специализации Data Science на русский язык, который весной запустили IBS и ABBYY LS.
Часть 1. О специальности Data Science в общих чертах. Курсы: Инструменты анализа данных (программирование на R); Предварительная обработка данных; Документирование процесса обработки данных.
Привет, Хабр!
Не так давно закончился мой 7-месячный марафон по освоению специализации «Наука о данных» (Data Science) на Coursera. Организационные стороны освоения специальности очень точно описаны тут. В своём посте я поделюсь впечатлениями от контента курсов. Надеюсь, после прочтения этой заметки каждый сможет сделать для себя выводы о том, стоит ли тратить время на получение знаний по аналитике данных или нет.
+27
Ближайшие события
Внешняя сортировка с O(1) дополнительной памяти
9 мин
37KПрочитав эту статью, я вспомнил, как писал внешнюю сортировку, которая использовала O(1) внешней памяти. Функция получала бинарый файл и максимальный размер памяти, которую она могла выделить под массив:
Я использовал алгоритм из Effective Performance of External Sorting with No Additional Disk Space:
Преимущество такого алгоритма, кроме отсутствия буфера на диске, это то, что с диска мы читаем данные относительно большими порциями, что ускоряет алгоритм.
Реализуем алгоритм на C++.
void ext_sort(const std::string filename, const size_t memory)
Я использовал алгоритм из Effective Performance of External Sorting with No Additional Disk Space:
- Разделим файл на блоки, которые помещаются в доступную память. Обозначим эти блоки Block_1, Block_2, …, Block_(S-1), Block_S. Установим P = 1.
- Читаем Block_P в память.
- Отсортируем данные в памяти и запишем назад в Block_P. Установим P = P + 1, и если P ≤ S, то читаем Block_P в память и повторяем этот шаг. Другими словами, отсортируем каждый блок файла.
- Разделим каждый блок на меньшие блоки B_1 и B_2. Каждый из таких блоков занимает половину доступной памяти.
- Читаем блок B_1 блока Block_1 в первую половину доступной памяти. Установим Q = 2.
- Читаем блок B_1 блока Block_Q во вторую половину доступной памяти.
- Объеденим массивы в памяти с помощью in-place слияния, запишем вторую половину памяти в блок B_1 блока Block_Q и установим Q = Q + 1, если Q ≤ S, читаем блок B_1 блока Block_Q во вторую половину доступной памяти и повторяем этот шаг.
- Записываем первую половину доступной памяти в блок B_1 блока Block_1. Так как мы всегда оставляли в памяти меньшую половину элементов и провели слияние со всеми блоками, то в этой части памяти хранятся M минимальных элементы всего файла.
- Читаем блок B_2 блока Block_S во вторую половину доступной памяти. Установим Q = S −1.
- Читаем блок B_2 блока Block_Q в первую половину доступной памяти.
- Объеденим массивы в памяти с помощью in-place слияния, запишем первую половину доступной памяти в блок B_2 блока Block_Q и установим Q = Q −1. Если Q ≥ 1 читаем блок B_2 блока Block_Q в первую половину доступной памяти и повторяем этот шаг.
- Записываем вторую половину доступной памяти в блок B_2 блока Block_S. Аналогично шагу 8, тут хранятся максимальные элементы всего файла.
- Начиная от блока B_2 блока Block_1 и до блока B_1 блока Block_S, определим новые блоки в файле и снова пронумеруем их Block_1 to Block_S. Разделим каждый блок на блоки B_1 и B_2. Установим P = 1.
- Читаем B_1 и B_2 блока Block_P в память. Объеденим массивы в памяти. запишем отсортированный массив назад в Block_P и установим P = P +1. Если P ≤ S, повторяем этот шаг.
- Если S > 1, возвращаемся к шагу 5. Каждый раз мы выделяем M минимальных и максимальных элементов, записываем их в начало и конец файла соответственно, а потом делаем то же самое с оставшимися элементами, пока не дойдем до середины файла.
Преимущество такого алгоритма, кроме отсутствия буфера на диске, это то, что с диска мы читаем данные относительно большими порциями, что ускоряет алгоритм.
Реализуем алгоритм на C++.
+17
Муравьиная оптимизация и сетевые алгоритмы
8 мин
20KПеревод
Как вы могли заметить, у нас тут затишье. Но наш творческий поиск не прекращается, и первая октябрьская публикация будет посвящена ACO (Ant Colony Optimization)

Отдавая должное автору, мы не будем публиковать здесь последнюю часть статьи, содержащую пример на JavaScript, а предложим вам опробовать его на сайте оригинала. Под катом же вы найдете перевод теоретической части, доступно рассказывающей о тонкостях муравьиной оптимизации в различных сценариях.

Отдавая должное автору, мы не будем публиковать здесь последнюю часть статьи, содержащую пример на JavaScript, а предложим вам опробовать его на сайте оригинала. Под катом же вы найдете перевод теоретической части, доступно рассказывающей о тонкостях муравьиной оптимизации в различных сценариях.
+15
Простой алгоритм распознавания движения
2 мин
21KКогда я начал работать над магистерской диссертацией на тему «Анализ пространственной структуры динамических изображений», то столкнулся с проблемой, что очень трудной найти какие-то готовые примеры алгоритмов распознавания образов и движущихся объектов. Везде, и в литературе, и в Интернете одна только голая теория. Цель написания данной статьи как раз восполнить данный пробел.
-5
Поисковые подсказки изнутри
11 мин
29K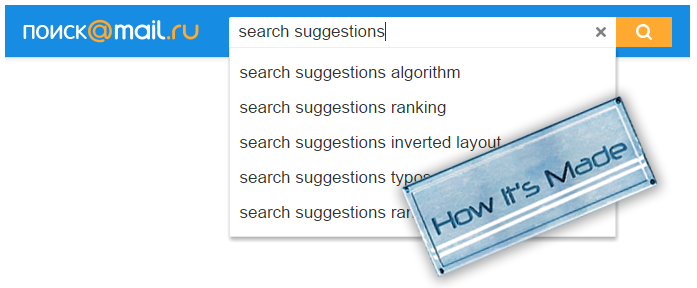
Ночная зала. Тысячи таинственных ликов в темноте, подсвеченных голубоватым свечением мониторов. Оглушительный треск миллиона клавиш. Подобные выстрелам автомата удары по клавишам «Enter». Зловещее стрекотание сотен тысяч мышек… Так, наверняка, играло воображение каждого разработчика высоконагруженной системы. И если его вовремя не остановить, то может выйти целый триллер или фильм ужасов. Но в данной статье мы будем гораздо ближе к земле. Мы кратко рассмотрим известные подходы к решению задачи поисковых подсказок, как мы научились делать их полнотекстовыми, а также расскажем о парочке уловок, на которые мы пошли, чтобы придать им скорости, но при этом не научить жадности к ресурсам. В конце статьи вас ждёт бонус — небольшой рабочий пример.
+55
Ищем стабильность в ритейле, XYZ–анализ ассортимента
7 мин
56KXYZ–анализ — одна из форм анализа товарного ассортимента магазина, сети или отдельной товарной группы в ритейле.

XYZ–анализ определяет стабильность продаж товара за определенный период. Полезен для управления ассортиментом и поставками товаров, организации работы с поставщиками. Результаты позволяют разделить товары по категориям и выделить для них место на складе, уровень запасов и организацию доставки.
Как отдельный метод анализа в ритейле XYZ используется не так уж часто, чаще его можно встретить как совмещенный с АВС анализом.
Но, в любом случае, как метод для принятия решений по управлению ассортиментом товарной группы или магазина может принести несомненную пользу.
Начнем с рассмотрения его особенностей и возможностей применения.

XYZ–анализ определяет стабильность продаж товара за определенный период. Полезен для управления ассортиментом и поставками товаров, организации работы с поставщиками. Результаты позволяют разделить товары по категориям и выделить для них место на складе, уровень запасов и организацию доставки.
Как отдельный метод анализа в ритейле XYZ используется не так уж часто, чаще его можно встретить как совмещенный с АВС анализом.
Но, в любом случае, как метод для принятия решений по управлению ассортиментом товарной группы или магазина может принести несомненную пользу.
Начнем с рассмотрения его особенностей и возможностей применения.
+8
Простой графический редактор с использованием OpenCV
5 мин
33KВ этой статье я расскажу, как достаточно быстро и просто написать редактор изображений на C++ с использованием библиотеки компьютерного зрения opencv. Реализованы такие эффекты, как насыщенность, экспозиция, резкость, контрастность и другие. Никакой магии!

Внимание! Под катом много графики и кода.

Внимание! Под катом много графики и кода.
+18
Хавала: Алгоритм работы системы подпольного банкинга, сохранившейся с древних времен
5 мин
103K
Несколько месяцев назад на Хабре был опубликован материал, в котором описывался алгоритм движения денег в банковской системе. Однако привычные нам банки — не единственный инструмент, которые жители разных стран мира используют для работы с финансами.
Одна из таких финансово-расчетных систем получила название «Хавала». Она зародилась в Индостане задолго до появления банковской системы западного образца (по разным оценкам, она работала уже в 8 веке), и до сих пор используется многими гражданами стран Среднего Востока, Африки и Азии в качестве альтернативного инструмента расчетов.
+19
Вклад авторов
alizar 2996.5ZlodeiBaal 1564.0Fil 1460.0agorkov 1345.0haqreu 1311.0Leono 1086.0YUVladimir 1037.0valemak 1014.0mephistopheies 996.0Zalina 922.0