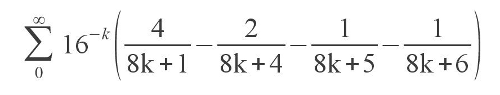Математика *

Многие слышали о великом и ужасном быстром преобразовании Фурье (БПФ / FFT — fast fourier transform) — но как его можно применять для решения практических задач за исключением JPEG/MPEG сжатия и разложения звука по частотам (эквалайзеры и проч.) — зачастую остается неясным вопросом.

Недавно я наткнулся на интересную реализацию игры «Жизнь» Конвея, использующую быстрое преобразование Фурье — и надеюсь, оно поможет вам понять применимость этого алгоритма в весьма неожиданных местах.

Начнём с объяснения, что же такое четырёхмерное пространство.


Это — одномерное пространство, то есть просто ось OX. Любая точка на ней характеризуется одной координатой.


Теперь проведём ось OY перпендикулярно оси OX. Вот и получилось двумерное пространство, то есть плоскость XOY. Любая точка на ней характеризуется двумя координатами — абсциссой и ординатой.


Проведём ось OZ перпендикулярно осям OX и OY. Получится трёхмерное пространство, в котором у любой точки есть абсцисса, ордината и аппликата.


Логично, что четвёртая ось, OQ, должна быть перпендикулярной осям OX, OY и OZ одновременно. Но мы не можем точно построить такую ось, и потому остаётся только попытаться представить её себе. У каждой точки в четырёхмерном пространстве есть четыре координаты: x, y, z и q.

С недавних пор существует элегантная формула для вычисления числа Пи, которую в 1995 году впервые опубликовали Дэвид Бэйли, Питер Борвайн и Саймон Плафф:


Казалось бы: что в ней особенного — формул для вычисления Пи великое множество: от школьного метода Монте-Карло до труднопостижимого интеграла Пуассона и формулы Франсуа Виета из позднего Средневековья. Но именно на эту формулу стоит обратить особое внимание — она позволяет вычислить n-й знак числа пи без нахождения предыдущих. За информацией о том, как это работает, а также за готовым кодом на языке C, вычисляющим 1 000 000-й знак, прошу под хабракат.

Затянувшееся продолжение цикла статей о теории игр.

Речь идет о необычных учебниках, которые стоят посередине между вузовскими учебниками и чисто научно-популярными брошюрами. Тем не менее между научпопом и такими учебниками есть четкий водораздел — последние нацелены именно на обучение, развлекательные фишки — лишь форма подачи серьезного материала. Общее для всех таких книг, как мне представляется — подача материала в виде комикса и\или в виде диалога двух или больше людей. Обычно два собеседника — ученик и учитель, один постоянно задает вопросы, часто глупые или смешные, второй пытается объяснить в игровой форме.

В посте много скриншотов нескольких книг. Одну из них, которая про катастрофы я полностью переснял и выложил pdf. Прошу учесть, под хабракатом не один мегабайт картинок, текста много меньше. Заранее прошу прощения за качество некоторых кадров — ночная пересъемка не способствовала. Возможно, картинок больше, чем нужно, но я старался и показать основные принципы — графический, игровой способ подачи материала, сюжет и диалоги.

Я сделал что-то вроде ретроспективы: первая книга — свежий японский комикс-манга о матстатистики издания 2010 года, дальше — книга из 80-х о математике, теории катасроф. Последняя — учебник радиоэлектроники для начинающих, знакомый нескольким поколениям читателей по всему миру, начиная с 30-х годов.

В качестве иллюстрации поста приведу обложку другой манги из той же серии, что и книга о статистике:

Занимаясь прогнозированием временных рядов, часто сталкиваюсь с идеей: «Вот бы реализовать такую модель прогнозирования, которая бы все-все учитывала и давала самый точный на свете прогноз». Утопия ли это? В ответе на этот вопрос окунулась в историю одного из самых сложных вопросов прогнозирования — прогнозирование погоды.

Представим воображаемого хитрого дядю, который хочет обмануть и заработать деньги на «лопухах». Назовем его Геннадий Обмануев.
В самый обычный вторник, Геннадию Обмануеву вдруг пришла гениальная идея: создать лотерею, в которой каждый игрок может сам указывать свой шанс на победу и, следовательно, множитель выигрыша и играть на выставленных им правилах! Для того, чтобы всегда оставаться в плюсе, Геннадий в конце каждой удачной игры берет символическую плату в 5% от выигрыша.


*если кратко об игре

Как и в случае с казино, чем дольше игрок играет в такую игру — тем более вероятно, что он, в конце концов, проиграет. Но неужели нельзя обмануть хитрого дядю, придумав чудесную тактику, благодаря которой можно увеличить свои шансы на победу?

Вместо вступления

В стандартной колоде для покера 54 карты. Без двух джокеров, которые не участвуют в игре, выходит 52 карты. Если вы хорошенько перемешаете колоду, то, возможно, создадите уникальную комбинацию из карт, которую никогда никто не создавал до вас. Потому что различных вариантов расположений 52 карт равно:


Что-то мне подсказывает, что комбинация на изображении не так уникальна.

Теперь к теме

Недавно я узнал про метод «барного развода» на игральных картах, благодаря которому «умные дяди» выигрывают приличные суммы. Суть такова:
«Разводчик» приходит в бар и некоторое время болтает с окружающими, чаще всего присоединяется к большим компаниям молодых людей. Он пытается влиться в компанию и стать «своим» среди окружающих. После того, как он заслужил некоторое доверие и к нему привыкли, разводчик выбирает самого вспыльчивого и разводит его на спор:

Я слышал, что у [блондинов/низких людей/тех, кто носит кепки/любой подходящий вариант] интуиция просто отстой! Вот спорим, что ты не сможешь угадать (в этот момент разводчик достает колоду карт) цвет каждой следующей карты? Можешь перетасовать колоду, как захочешь! За каждую угаданную карту плачу по тысяче рублей! А если не угадаешь, то ты даешь мне два рубля, потом докидываешь до четырех, до восьми рублей и дальше, ну ты понял? И чтобы было честно — остановить игру может лишь тот, кто проигрывает в общем счете, у кого выигрыш меньше. Идет?

Большинство читателей уже поняли схему и с улыбкой прикидывают сумму, которую может выиграть разводчик.
Мне стало интересно, до каких пор игрок выигрывает и как нужно действовать, чтобы увеличить шансы на выигрыш (лучший способ — отказаться от игры!). Естественно, правило про остановку игры я не учитываю, с ним выиграть невозможно.

Первая часть
Первая часть второй части
Вторая часть второй части

Ну что ж, господа, пора заканчивать. В последней статье цикла (название которой разрывает мой ещё толком не проснувшийся шаблон) мы поставим жирную точку в истории этой задачи. Несмотря на то, что в комментариях ко второй части был предложен более удобный и универсальный способ это сделать, я всё же воспользуюсь инструментарием, разработанным лично мной ещё до написания первой из статей. Во-первых, не пропадать же добру, а во-вторых, я думаю, все понимают, что задача — это просто повод порисовать красивые чертёжики в GeoGebra и запостить их на хабр. Ну, как говорится, понеслась.

Первая часть
Первая часть второй части

Майские праздники продолжаются, количество употреблений слова «часть» на строку текста зашкаливает, а мы с вами, дорогие читатели, наконец прикончим случай поворота с центром внутри фигуры.

Введение

Среди людей бытует мнение, что человек, поступивший на математический факультет, обязательно выйдет оттуда учителем математики. Это не я придумал, это по опыту, ибо довольно большое количество не очень образованных людей спрашивало, куда я собираюсь идти работать после окончания ВУЗа. Разумеется, найти можно и куда более обширные области применения своих знаний. Одна из них связана с теорией вероятности. Я не хочу вникать в сложные подробности предмета, т.к. люди, не имеющие нужной математической базы, скорее всего запутаются. Но и говорить совсем ни о чем не хочется. Поэтому я хочу написать про связь человека и этой самой теории вероятностей, причем на простом, понятном любому языке. Если интересно — прошу под кат.

Теория динамического хаоса давно является популярной (можно сказать, «модной») темой среди интеллектуалов — технарей, айтишников, даже гуманитариев.
Околонаучные книги и интернет-страницы о хаосе экплуатируют одни и те же модели, известные чуть ли не с XIX века: фракталы, турбулентность, логистическое отображение…
Между тем, в последние 10 лет стало понятно, что динамический хаос (наравне с самоорганизацией) —
ключ к пониманию мироздания, в том числе происхождения и работы нашего сознания.
Серьёзные монографии на эту тему требуют высокого уровня подготовки и математической культуры.
(У кого таковой имеется, рекомендую:
А.Б. Каток, Б. Хасселблат «Введение в современную теорию динамических систем»).
Разумеется, есть примеры сбалансированного подхода:

• Г.М. Заславский, Р.М. Сагдеев «Введение в нелинейную физику»
• С.П. Кузнецов «Динамический хаос»
• А. Лихтенберг, М. Либерман «Регулярная и стохастическая динамика»

расчитанные на уровень 2-3 курса техвуза.
Есть и сайты содержательные:
Саратовская группа нелинейной динамики
Загадочный сайт

Вот довольно свежая, интересная публикация об иерархии хаоса, критериях стохастичности.
Математика там только выглядит пугающе; достаточно знания теории множеств.
Здесь я хотел бы осветить похожую тему: разобрать один из критериев случайности и
предложить домашний эксперимент для само-анализа.

С первой частью можно невозбранно ознакомиться здесь.

Итак, дорогие друзья, в предыдущей части мы с вами поговорили о параллельном переносе, а сегодня займёмся поворотом. Это будет интересно. Сейчас быстренько вспомним основные понятия — и вперёд.

Недавно прочитал пост о диллемме заключенных, который заинтересовал сообщество.
В данном посте хочу показать взгляд на эту проблему со стороны теории игр, на основе опыта полученного после обучения на онлайн курсах ИИ университета в Беркли. После применения данного аппарата проблема становится понятной и разрешимой.

Задачи на разрезание — это та область математики, где, как говорится, мамонт не валялся. Множество отдельных проблем, но по сути нет общей теории. Помимо всем известной теоремы Бойяи-Гервина, других фундаментальных результатов в этой области практически нет. Неопределённость — вечный спутник задач на разрезание. Мы можем, например, разрезать правильный пятиугольник на шесть частей, из которых можно сложить квадрат; однако мы не можем доказать, что пяти частей для этого было бы недостаточно.

С помощью хитрой эвристики, воображения и поллитры нам порой удаётся найти конкретное решение, но, как правило, мы не обладаем подходящим инструментарием, чтобы доказать минимальность этого решения или же его несуществование (последнее, разумеется, относится к случаю, когда мы решение не нашли). Это печально и несправедливо. И как-то раз я взял чистую тетрадку и решил восстановить справедливость в масштабах одной конкретной задачи: разрезания плоской фигуры на две равных (конгруэнтных) части. В рамках этого цикла статей (их, кстати, будет три) мы с вами, камрады, рассмотрим вот этот забавный многоугольник, изображённый ниже, и попытаемся беспристрастно разобраться, можно ли разрезать его на две равных фигуры, или же таки нет.

Добрый день, уважаемые коллеги. В этой статье я хочу поделиться с Вами своими методическими наработками, которые использую в курсе «Теория автоматического управления» на кафедре СУиИ НИУ ИТМО.
Основной задачей, которую я перед собой ставил, было объединение теоретических знаний для решения практической задачи. Такой задачей стало управление приводами Lego робота. Лишний повод поиграть в игрушки, да и студентам проще воспринимать суровый матан… Вот пример описания этого набора: habrahabr.ru/post/166449.

В компании Intel разрабатывается довольно много ПО для моделирования различных физических процессов. В некоторых из них мы используем пакет OpenFOAM, и в этом посте я постараюсь дать краткое описание его возможностей.
Что такое OpenFOAM? Это, пользуясь термином Википедии, открытая (GPL) платформа для численнного моделирования — в первую очередь для моделирования, связанного с решением уравнений в частных производных методом конечных объемов, и в самую первую очередь — для решения задач механики сплошных сред.
КПДВ: эволюция двух несмешивающихся жидкостей разной плотности, изначально разделенных тонкой перегородкой (пример «lockExchange» из стандартной поставки OpenFOAM). Переходные цвета обозначают ячейки сетки, где присутствует доля и той, и другой жидкости (более точно: при симуляции используется метод объёма жидкости).

Небольшое предисловие

Этот текст является продолжением поста , в котором автор попытался как можно более просто и без сложных математических выкладок описать понятия формального языка и грамматики. На этот текст пришло достаточно много откликов и автор счел себя обязанным написать продолжение.

Ниже описывается формализм порождающих грамматик Хомского. Методы задания языка с помощью порождающих грамматик сейчас довольно популярны, особенно для машинной обработки компьютерных языков. Но обычно изучение порождающих грамматик в теории трансляторов заканчивается на контекстно-свободных грамматиках. Последние являются довольно узким специальным классом порождающих грамматик Хомского и обычно используются как вид категориальных грамматик (как конкретно это делается, будет показано ниже) для задания синтаксических анализаторов. Последнее обстоятельство только затуманивает понимание подхода Хомского. Дальнейшее изложение предназначено тем, кому интересно понять, в чем состоит этот подход.

Я сам пытаюсь быть где-то посредине между «глобальными заговорщиками» и нашими «борцами за экологию», ибо считаю, что истина где-то именно там…

Недавно был День Земли и, почитав немного на Википедии о Часе Земли и, особенно, раздел Критика, я дошел до интересной статьи Константина Ранкса Как вредит экологии борьба с глобальным потеплением. Там утверждается, что современная мощность автомобилей в 37 раз больше мощности все электростанций мира. Откуда взяты данные для этих расчетов — не сказано. Захотелость проверить самому, но как? Гуглить в поисках исходных данных? Можно, но долго, ненадежно и скучно. Есть и другой путь, не менее интересный!

Как-то еще в школе в «Кванте» читал статейку о задачах Ферми и ее классический пример о количестве молекул резины, стираемых за один оборот колеса. Вот и захотелось попробовать применить этот же метод и «прикинуть» числа в нашем случае.
Скорее всего, я не учел много фактов, о которых вы позже укажете в комментариях, но, как я и писал выше, истину найдем где-то посредине…

Я занимаюсь прогнозированием временных рядов уже более 5 лет. В прошлом году мною была защищена диссертация по теме «Модель прогнозирования временных рядов по выборке максимального подобия», однако вопросов после защиты осталось порядочно. Вот один из них — общая классификация методов и моделей прогнозирования.

Обычно в работах как отечественных, так и англоязычных авторы не задаются вопросом классификации методов и моделей прогнозирования, а просто их перечисляют. Но мне кажется, что на сегодняшний день данная область так разрослась и расширилась, что пусть самая общая, но классификация необходима. Ниже представлен мой собственный вариант общей классификации.

В чем разница между методом и моделью прогнозирования?

Метод прогнозирования представляет собой последовательность действий, которые нужно совершить для получения модели прогнозирования. По аналогии с кулинарией метод есть последовательность действий, согласно которой готовится блюдо — то есть сделается прогноз.

Модель прогнозирования есть функциональное представление, адекватно описывающее исследуемый процесс и являющееся основой для получения его будущих значений. В той же кулинарной аналогии модель есть список ингредиентов и их соотношение, необходимый для нашего блюда — прогноза.

Совокупность метода и модели образуют полный рецепт!