Я всё продолжаю возиться со своими микрофотографиями. Наука не стоит на месте (с момента той статьи прошел без двух месяцев год!), и теперь нам нужно распознавать другие объекты:

Но тут уже безо всяких послаблений: точность должна быть достаточно высокой.
Конкретно эта задачка встала недавно (примерно в конце ноября), и решалась в свободное от учёбы и работы время.
Achtung! Статья получилась довольно крупная, много картинок. Зато без избыточной математики.
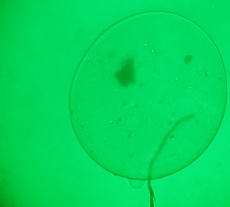
Сформулируем задачу: получить параметры, полностью характеризующие контур фигуры, изображенной на картинке.
Тут у меня есть преимущество: я знаю, как эти частицы делаются, и также знаю, что они всегда эллиптической формы, причём форма эта стремится к идеальной. Идеальный эллипс описывается уравнением кривой второго порядка:
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
Таким образом, задачка сводится в нахождению всех этих параметров. Для их нахождения, нам нужно узнать координаты шести любых точек, заведомо лежащих на эллипсе (число точек = числу неизвестных в полном уравнении второго порядка приведенном выше): тогда мы сможем найти все необходимые нам параметры эллипса (о том, как аппроксимировать шесть точек эллипсом читайте ниже, сейчас мы решаем другую задачу). Собственно, мной тут же была написана программа, где пользователь мог ткнуть мышкой шесть точек и программа выдавала площадь эллипса. Написана быстро, и именно с ёё помощью я защитил курсовую работу неделю назад.
Но как выбрать точки автоматически? Очень просто: помните статью про решение судоку? Там автор использует превосходный алгоритм нахождения особых точек изображения (читай границ на изображении).
Вкратце, в чём его суть: для нахождения границ, мы не задаём одну границу интенсивности (которая колеблется от 0 до 255), относительно которой пиксели перекрашиваются либо в белый, либо в чёрный цвет (если интенсивность меньше заданной границы — пиксель черный, иначе — белый). Такой подход используется в методе Отсу, и ничего хорошего в нём, кроме скорости выполнения нет. Очень узконаправленный алгоритм. Вместо этого лучше использовать «плавающую» границу интенсивности. Вокруг исследуемого пикселя выбирается область, известного размера (я использовал область размером 11х11 пикселей). Если его интенсивность меньше средней интенсивности всех пикселей в области — то он — фон, и его закрашивают белым. Если его интенсивность больше, то его закрашивают черным. Короткая схемка приведена на рисунке ниже:

Результат работы этого алгоритма почти устраивает. Вот примерно такой результат мы получим, следуя этому алгоритму:

Увидев это — немедленно было принято решение немного «завысить» значение средней интенсивности. Искусственно подняв это значение на 15 единиц, я пришел к такому результату:

И этот результат устроил меня чуть более, чем полностью. Потому что на нём кроме очертаний моего эллипса практически ничего нет. Это уже само по себе превосходно!
Но нам нужно двигаться дальше. Помните, для чего мы всё это затевали? Нам нужно по шести точкам, лежащим на эллипсе, определить параметры полного уравнения кривой второго порядка. На данный момент мы ещё далеки от окончательного решения, ведь мы нашли только массив точек (черные точки), которые могут претендовать на нужные нам. Однако, нам подойдут далеко не все точки… Почему именно, я решил показать картинкой:

Если точки расположены слишком близко друг к другу, то через заданные шесть точек можно провести как минимум два эллипса с одинаковой достоверностью. Поэтому выбираемые шесть точек должны лежать как можно дальше друг от друга. Плюс, заведомо лежать на эллипсе.
Тут было над чем подумать, и я действительно завис на недельку. Однако его святейшество, функция Math.Rand() спасла меня.
Было решено вынимать случайные шесть точек из массива, и по ним строить эллипс. И так много-много раз (эмпирически для изображения размером 700х700 пикселей — достаточно двух тысяч итераций)
Результат оправдал все мои ожидания: у меня получилось. Функция, преобразующая шесть точек в эллипс (её алгоритм приведен чуть ниже), возвращала координаты центра эллипса, длины двух его осей, и угол его поворота относительно осей координат. Я решил для ясности вновь нарисовать схемку:

Из полученных данных можно было построить зависимость x = f(y), где (x,y) — это координаты центра эллипса; а также зависимость R1 = f(R2) — где R1 и R2 — это длины осей эллипса. Точка — в которой полученные координаты встречаются чаще всего — наша искомая точка (координата координат, пардон за тавтологию).
Чтобы было понятнее — приведу фрагмент такого «распыления» полученного массива точек на плоскость.
Распыление координат центра эллипса:
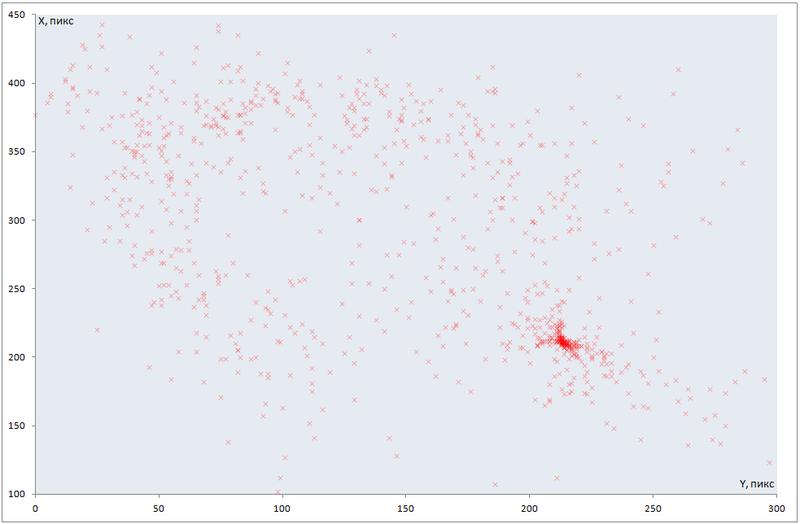
Как видно невооруженным взглядом — максимум находится примерно при X=210, Y=220; Эти точки и есть координаты центра нашего изображения.
Как искать максимум скопления точек? Ооо… Я тут (на Хабре) задал вопрос — один человек (не будем тыкать пальцем в Monnoroch) мне такого насоветовал, что лучи ненависти в его сторону. Но были и классные ответы, в том числе и в личку, спасибо всем откликнувшимся! Однако я всё равно пошел своим путём.
Я взял и создал пустой массив counter[][], размерностью как исходное изображение. И начал перебирать полученный в результате двух тысяч итераций массив точек (x,y). Если поле пустое, то, естественно, я ничего не делал. Однако, как только попадается точка, то, во-первых, делаем counter[x][y] = counter[x][y] +2, а во-вторых увеличиваем счетчик также и у всех соседей. Уж простите меня за эти схемы, но вот ещё одна :)
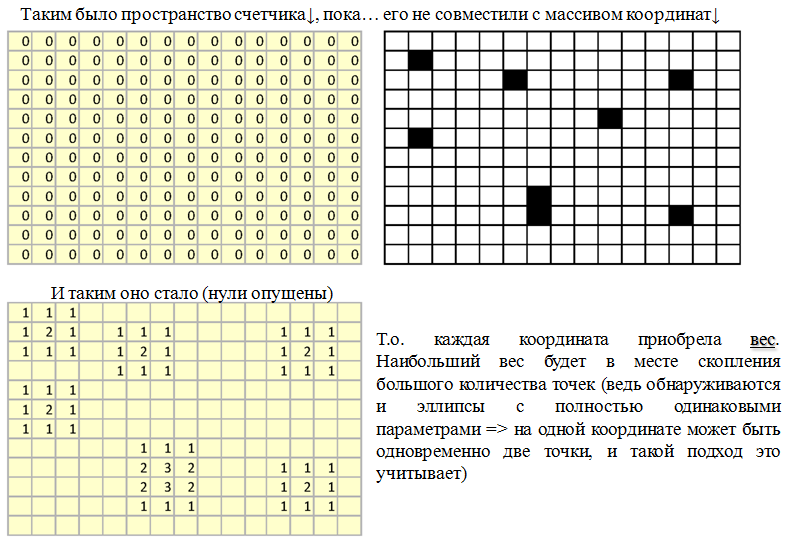
Абсолютно идентичная картина и в случае с перебором полученного массива длин осей эллипса, чтобы вконец не загромождать статью, я не буду приводить картинки для них. Поверьте — абсолютно то же самое.
Ну вот и всё. Максимумы найдены, а значит координаты, длины осей и угол поворота известны. Всё! :)
Результат работы алгоритма на самой первой картинке из статьи:

P.S. Отдельно большое спасибо хабраюзеру ruedj, который за просто так отдал мне свой двухтомник (2011 год!) Хорстманна, и я наконец-то научился более-менее правильно общаться с многопоточностью. Весь алгоритм на изображении 700х700 точек на core i3-2100 (одна из самых слабых моделей в линейке Sandy Bridge) занимает ~1000ms.
Но тут уже безо всяких послаблений: точность должна быть достаточно высокой.
Конкретно эта задачка встала недавно (примерно в конце ноября), и решалась в свободное от учёбы и работы время.
Achtung! Статья получилась довольно крупная, много картинок. Зато без избыточной математики.
Сформулируем задачу: получить параметры, полностью характеризующие контур фигуры, изображенной на картинке.
Тут у меня есть преимущество: я знаю, как эти частицы делаются, и также знаю, что они всегда эллиптической формы, причём форма эта стремится к идеальной. Идеальный эллипс описывается уравнением кривой второго порядка:
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
Таким образом, задачка сводится в нахождению всех этих параметров. Для их нахождения, нам нужно узнать координаты шести любых точек, заведомо лежащих на эллипсе (число точек = числу неизвестных в полном уравнении второго порядка приведенном выше): тогда мы сможем найти все необходимые нам параметры эллипса (о том, как аппроксимировать шесть точек эллипсом читайте ниже, сейчас мы решаем другую задачу). Собственно, мной тут же была написана программа, где пользователь мог ткнуть мышкой шесть точек и программа выдавала площадь эллипса. Написана быстро, и именно с ёё помощью я защитил курсовую работу неделю назад.
Но как выбрать точки автоматически? Очень просто: помните статью про решение судоку? Там автор использует превосходный алгоритм нахождения особых точек изображения (читай границ на изображении).
Вкратце, в чём его суть: для нахождения границ, мы не задаём одну границу интенсивности (которая колеблется от 0 до 255), относительно которой пиксели перекрашиваются либо в белый, либо в чёрный цвет (если интенсивность меньше заданной границы — пиксель черный, иначе — белый). Такой подход используется в методе Отсу, и ничего хорошего в нём, кроме скорости выполнения нет. Очень узконаправленный алгоритм. Вместо этого лучше использовать «плавающую» границу интенсивности. Вокруг исследуемого пикселя выбирается область, известного размера (я использовал область размером 11х11 пикселей). Если его интенсивность меньше средней интенсивности всех пикселей в области — то он — фон, и его закрашивают белым. Если его интенсивность больше, то его закрашивают черным. Короткая схемка приведена на рисунке ниже:
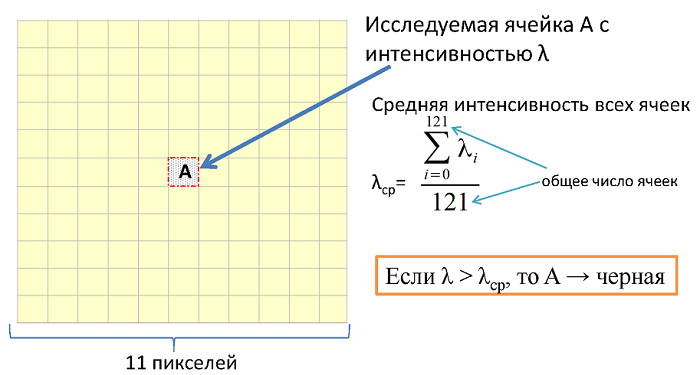
Результат работы этого алгоритма почти устраивает. Вот примерно такой результат мы получим, следуя этому алгоритму:

Увидев это — немедленно было принято решение немного «завысить» значение средней интенсивности. Искусственно подняв это значение на 15 единиц, я пришел к такому результату:

И этот результат устроил меня чуть более, чем полностью. Потому что на нём кроме очертаний моего эллипса практически ничего нет. Это уже само по себе превосходно!
Но нам нужно двигаться дальше. Помните, для чего мы всё это затевали? Нам нужно по шести точкам, лежащим на эллипсе, определить параметры полного уравнения кривой второго порядка. На данный момент мы ещё далеки от окончательного решения, ведь мы нашли только массив точек (черные точки), которые могут претендовать на нужные нам. Однако, нам подойдут далеко не все точки… Почему именно, я решил показать картинкой:
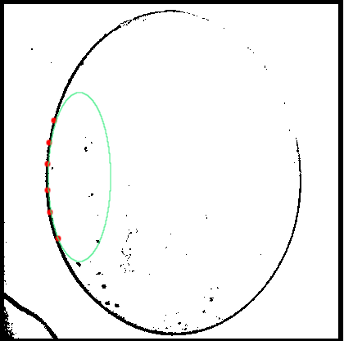
Если точки расположены слишком близко друг к другу, то через заданные шесть точек можно провести как минимум два эллипса с одинаковой достоверностью. Поэтому выбираемые шесть точек должны лежать как можно дальше друг от друга. Плюс, заведомо лежать на эллипсе.
Тут было над чем подумать, и я действительно завис на недельку. Однако его святейшество, функция Math.Rand() спасла меня.
Было решено вынимать случайные шесть точек из массива, и по ним строить эллипс. И так много-много раз (эмпирически для изображения размером 700х700 пикселей — достаточно двух тысяч итераций)
Результат оправдал все мои ожидания: у меня получилось. Функция, преобразующая шесть точек в эллипс (её алгоритм приведен чуть ниже), возвращала координаты центра эллипса, длины двух его осей, и угол его поворота относительно осей координат. Я решил для ясности вновь нарисовать схемку:

Из полученных данных можно было построить зависимость x = f(y), где (x,y) — это координаты центра эллипса; а также зависимость R1 = f(R2) — где R1 и R2 — это длины осей эллипса. Точка — в которой полученные координаты встречаются чаще всего — наша искомая точка (координата координат, пардон за тавтологию).
Чтобы было понятнее — приведу фрагмент такого «распыления» полученного массива точек на плоскость.
Распыление координат центра эллипса:
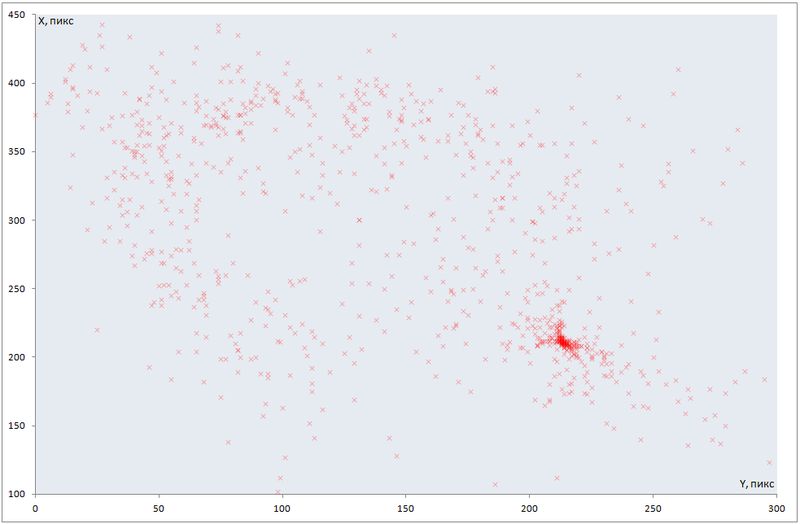
Как видно невооруженным взглядом — максимум находится примерно при X=210, Y=220; Эти точки и есть координаты центра нашего изображения.
Как искать максимум скопления точек? Ооо… Я тут (на Хабре) задал вопрос — один человек (не будем тыкать пальцем в Monnoroch) мне такого насоветовал, что лучи ненависти в его сторону. Но были и классные ответы, в том числе и в личку, спасибо всем откликнувшимся! Однако я всё равно пошел своим путём.
Я взял и создал пустой массив counter[][], размерностью как исходное изображение. И начал перебирать полученный в результате двух тысяч итераций массив точек (x,y). Если поле пустое, то, естественно, я ничего не делал. Однако, как только попадается точка, то, во-первых, делаем counter[x][y] = counter[x][y] +2, а во-вторых увеличиваем счетчик также и у всех соседей. Уж простите меня за эти схемы, но вот ещё одна :)
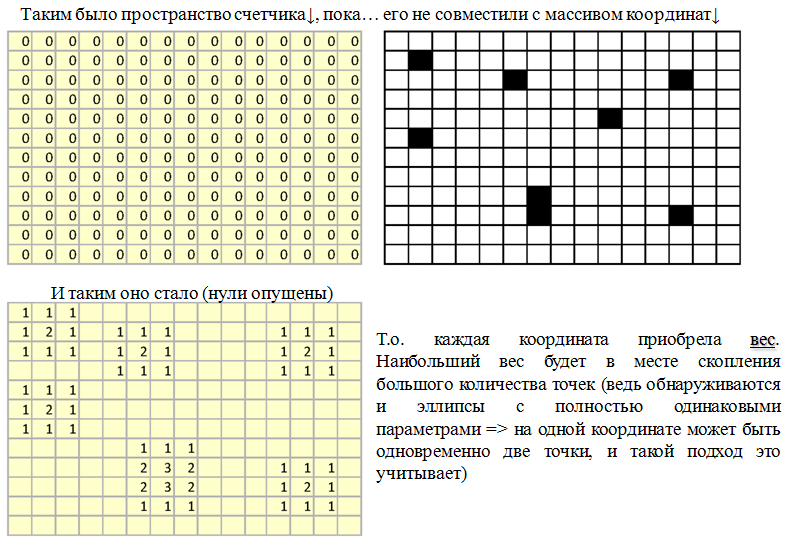
Абсолютно идентичная картина и в случае с перебором полученного массива длин осей эллипса, чтобы вконец не загромождать статью, я не буду приводить картинки для них. Поверьте — абсолютно то же самое.
Ну вот и всё. Максимумы найдены, а значит координаты, длины осей и угол поворота известны. Всё! :)
Результат работы алгоритма на самой первой картинке из статьи:

P.S. Отдельно большое спасибо хабраюзеру ruedj, который за просто так отдал мне свой двухтомник (2011 год!) Хорстманна, и я наконец-то научился более-менее правильно общаться с многопоточностью. Весь алгоритм на изображении 700х700 точек на core i3-2100 (одна из самых слабых моделей в линейке Sandy Bridge) занимает ~1000ms.





