 Если в одном из моих прошлых постов речь шла о довольно современном подходе к построению сбалансированных деревьев поиска, то этот пост посвящен реализации АВЛ-деревьев — наверное, самого первого вида сбалансированных двоичных деревьев поиска, придуманных еще в 1962 году нашими (тогда советскими) учеными Адельсон-Вельским и Ландисом. В сети можно найти много реализаций АВЛ-деревьев (например, тут), но все, что лично я видел, не внушает особенного оптимизма, особенно, если пытаешься разобраться во всем с нуля. Везде утверждается, что АВЛ-деревья проще красно-черных деревьев, но глядя на прилагаемый к этому код, начинаешь сомневаться в данном утверждении. Собственно, желание объяснить на пальцах, как устроены АВЛ-деревья, и послужило мотивацией к написанию данного поста. Изложение иллюстрируется кодом на С++.
Если в одном из моих прошлых постов речь шла о довольно современном подходе к построению сбалансированных деревьев поиска, то этот пост посвящен реализации АВЛ-деревьев — наверное, самого первого вида сбалансированных двоичных деревьев поиска, придуманных еще в 1962 году нашими (тогда советскими) учеными Адельсон-Вельским и Ландисом. В сети можно найти много реализаций АВЛ-деревьев (например, тут), но все, что лично я видел, не внушает особенного оптимизма, особенно, если пытаешься разобраться во всем с нуля. Везде утверждается, что АВЛ-деревья проще красно-черных деревьев, но глядя на прилагаемый к этому код, начинаешь сомневаться в данном утверждении. Собственно, желание объяснить на пальцах, как устроены АВЛ-деревья, и послужило мотивацией к написанию данного поста. Изложение иллюстрируется кодом на С++.Понятие АВЛ-дерева
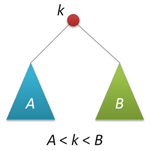 АВЛ-дерево — это прежде всего двоичное дерево поиска, ключи которого удовлетворяют стандартному свойству: ключ любого узла дерева не меньше любого ключа в левом поддереве данного узла и не больше любого ключа в правом поддереве этого узла. Это значит, что для поиска нужного ключа в АВЛ-дереве можно использовать стандартный алгоритм. Для простоты дальнейшего изложения будем считать, что все ключи в дереве целочисленны и не повторяются.
АВЛ-дерево — это прежде всего двоичное дерево поиска, ключи которого удовлетворяют стандартному свойству: ключ любого узла дерева не меньше любого ключа в левом поддереве данного узла и не больше любого ключа в правом поддереве этого узла. Это значит, что для поиска нужного ключа в АВЛ-дереве можно использовать стандартный алгоритм. Для простоты дальнейшего изложения будем считать, что все ключи в дереве целочисленны и не повторяются.Особенностью АВЛ-дерева является то, что оно является сбалансированным в следующем смысле: для любого узла дерева высота его правого поддерева отличается от высоты левого поддерева не более чем на единицу. Доказано, что этого свойства достаточно для того, чтобы высота дерева логарифмически зависела от числа его узлов: высота h АВЛ-дерева с n ключами лежит в диапазоне от log2(n + 1) до 1.44 log2(n + 2) − 0.328. А так как основные операции над двоичными деревьями поиска (поиск, вставка и удаление узлов) линейно зависят от его высоты, то получаем гарантированную логарифмическую зависимость времени работы этих алгоритмов от числа ключей, хранимых в дереве. Напомним, что рандомизированные деревья поиска обеспечивают сбалансированность только в вероятностном смысле: вероятность получения сильно несбалансированного дерева при больших n хотя и является пренебрежимо малой, но остается не равной нулю.
Структура узлов
Будем представлять узлы АВЛ-дерева следующей структурой:
struct node // структура для представления узлов дерева
{
int key;
unsigned char height;
node* left;
node* right;
node(int k) { key = k; left = right = 0; height = 1; }
};
Поле key хранит ключ узла, поле height — высоту поддерева с корнем в данном узле, поля left и right — указатели на левое и правое поддеревья. Простой конструктор создает новый узел (высоты 1) с заданным ключом k.
Традиционно, узлы АВЛ-дерева хранят не высоту, а разницу высот правого и левого поддеревьев (так называемый balance factor), которая может принимать только три значения -1, 0 и 1. Однако, заметим, что эта разница все равно хранится в переменной, размер которой равен минимум одному байту (если не придумывать каких-то хитрых схем «эффективной» упаковки таких величин). Вспомним, что высота h < 1.44 log2(n + 2), это значит, например, что при n=109 (один миллиард ключей, больше 10 гигабайт памяти под хранение узлов) высота дерева не превысит величины h=44, которая с успехом помещается в тот же один байт памяти, что и balance factor. Таким образом, хранение высот с одной стороны не увеличивает объем памяти, отводимой под узлы дерева, а с другой стороны существенно упрощает реализацию некоторых операций.
Определим три вспомогательные функции, связанные с высотой. Первая является оберткой для поля height, она может работать и с нулевыми указателями (с пустыми деревьями):
unsigned char height(node* p)
{
return p?p->height:0;
}
Вторая вычисляет balance factor заданного узла (и работает только с ненулевыми указателями):
int bfactor(node* p)
{
return height(p->right)-height(p->left);
}
Третья функция восстанавливает корректное значение поля height заданного узла (при условии, что значения этого поля в правом и левом дочерних узлах являются корректными):
void fixheight(node* p)
{
unsigned char hl = height(p->left);
unsigned char hr = height(p->right);
p->height = (hl>hr?hl:hr)+1;
}
Заметим, что все три функции являются нерекурсивными, т.е. время их работы есть величина О(1).
Балансировка узлов
В процессе добавления или удаления узлов в АВЛ-дереве возможно возникновение ситуации, когда balance factor некоторых узлов оказывается равными 2 или -2, т.е. возникает расбалансировка поддерева. Для выправления ситуации применяются хорошо нам известные повороты вокруг тех или иных узлов дерева. Напомню, что простой поворот вправо (влево) производит следующую трансформацию дерева:
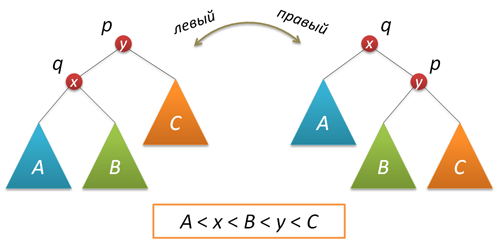
Код, реализующий правый поворот, выглядит следующим образом (как обычно, каждая функция, изменяющая дерево, возвращает новый корень полученного дерева):
node* rotateright(node* p) // правый поворот вокруг p
{
node* q = p->left;
p->left = q->right;
q->right = p;
fixheight(p);
fixheight(q);
return q;
}
Левый поворот является симметричной копией правого:
node* rotateleft(node* q) // левый поворот вокруг q
{
node* p = q->right;
q->right = p->left;
p->left = q;
fixheight(q);
fixheight(p);
return p;
}
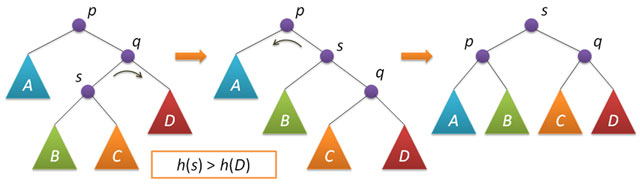
Рассмотрим теперь ситуацию дисбаланса, когда высота правого поддерева узла p на 2 больше высоты левого поддерева (обратный случай является симметричным и реализуется аналогично). Пусть q — правый дочерний узел узла p, а s — левый дочерний узел узла q.
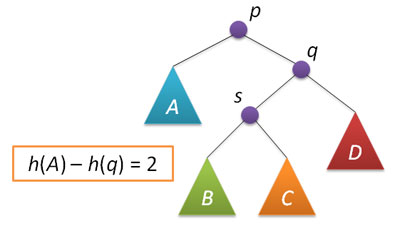
Анализ возможных случаев в рамках данной ситуации показывает, что для исправления расбалансировки в узле p достаточно выполнить либо простой поворот влево вокруг p, либо так называемый большой поворот влево вокруг того же p. Простой поворот выполняется при условии, что высота левого поддерева узла q больше высоты его правого поддерева: h(s)≤h(D).
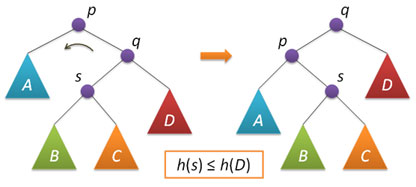
Большой поворот применяется при условии h(s)>h(D) и сводится в данном случае к двум простым — сначала правый поворот вокруг q и затем левый вокруг p.
Код, выполняющий балансировку, сводится к проверке условий и выполнению поворотов:
node* balance(node* p) // балансировка узла p
{
fixheight(p);
if( bfactor(p)==2 )
{
if( bfactor(p->right) < 0 )
p->right = rotateright(p->right);
return rotateleft(p);
}
if( bfactor(p)==-2 )
{
if( bfactor(p->left) > 0 )
p->left = rotateleft(p->left);
return rotateright(p);
}
return p; // балансировка не нужна
}
Описанные функции поворотов и балансировки также не содержат ни циклов, ни рекурсии, а значит выполняются за постоянное время, не зависящее от размера АВЛ-дерева.
Вставка ключей
Вставка нового ключа в АВЛ-дерево выполняется, по большому счету, так же, как это делается в простых деревьях поиска: спускаемся вниз по дереву, выбирая правое или левое направление движения в зависимости от результата сравнения ключа в текущем узле и вставляемого ключа. Единственное отличие заключается в том, что при возвращении из рекурсии (т.е. после того, как ключ вставлен либо в правое, либо в левое поддерево, и это дерево сбалансировано) выполняется балансировка текущего узла. Строго доказывается, что возникающий при такой вставке дисбаланс в любом узле по пути движения не превышает двух, а значит применение вышеописанной функции балансировки является корректным.
node* insert(node* p, int k) // вставка ключа k в дерево с корнем p
{
if( !p ) return new node(k);
if( k<p->key )
p->left = insert(p->left,k);
else
p->right = insert(p->right,k);
return balance(p);
}
Чтобы проверить соответствие реализованного алгоритма вставки теоретическим оценкам для высоты АВЛ-деревьев, был проведен несложный вычислительный эксперимент. Генерировался массив из случайно расположенных чисел от 1 до 10000, далее эти числа последовательно вставлялись в изначально пустое АВЛ-дерево и измерялась высота дерева после каждой вставки. Полученные результаты были усреднены по 1000 расчетам. На следующем графике показана зависимость от n средней высоты (красная линия); минимальной высоты (зеленая линия); максимальной высоты (синяя линия). Кроме того, показаны верхняя и нижняя теоретические оценки.
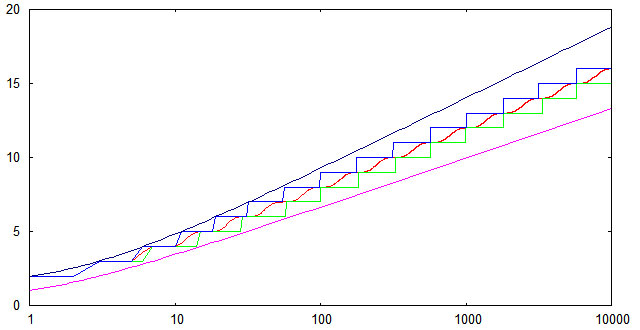
Видно, что для случайных последовательностей ключей экспериментально найденные высоты попадают в теоретические границы даже с небольшим запасом. Нижняя граница достижима (по крайней мере в некоторых точках), если исходная последовательность ключей является упорядоченной по возрастанию.
Удаление ключей
С удалением узлов из АВЛ-дерева, к сожалению, все не так шоколадно, как с рандомизированными деревьями поиска. Способа, основанного на слиянии (join) двух деревьев, ни найти, ни придумать не удалось.
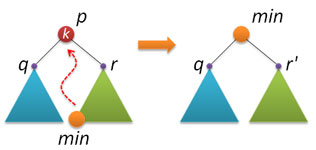 Поэтому за основу был взят вариант, описываемый практически везде (и который обычно применяется и при удалении узлов из стандартного двоичного дерева поиска). Идея следующая: находим узел p с заданным ключом k (если не находим, то делать ничего не надо), в правом поддереве находим узел min с наименьшим ключом и заменяем удаляемый узел p на найденный узел min.
Поэтому за основу был взят вариант, описываемый практически везде (и который обычно применяется и при удалении узлов из стандартного двоичного дерева поиска). Идея следующая: находим узел p с заданным ключом k (если не находим, то делать ничего не надо), в правом поддереве находим узел min с наименьшим ключом и заменяем удаляемый узел p на найденный узел min. При реализации возникает несколько нюансов. Прежде всего, если у найденный узел p не имеет правого поддерева, то по свойству АВЛ-дерева слева у этого узла может быть только один единственный дочерний узел (дерево высоты 1), либо узел p вообще лист. В обоих этих случаях надо просто удалить узел p и вернуть в качестве результата указатель на левый дочерний узел узла p.
Пусть теперь правое поддерево у p есть. Находим минимальный ключ в этом поддереве. По свойству двоичного дерева поиска этот ключ находится в конце левой ветки, начиная от корня дерева. Применяем рекурсивную функцию:
node* findmin(node* p) // поиск узла с минимальным ключом в дереве p
{
return p->left?findmin(p->left):p;
}
Еще одна служебная функция у нас будет заниматься удалением минимального элемента из заданного дерева. Опять же, по свойству АВЛ-дерева у минимального элемента справа либо подвешен единственный узел, либо там пусто. В обоих случаях надо просто вернуть указатель на правый узел и по пути назад (при возвращении из рекурсии) выполнить балансировку. Сам минимальный узел не удаляется, т.к. он нам еще пригодится.
node* removemin(node* p) // удаление узла с минимальным ключом из дерева p
{
if( p->left==0 )
return p->right;
p->left = removemin(p->left);
return balance(p);
}
Теперь все готово для реализации удаления ключа из АВЛ-дерева. Сначала находим нужный узел, выполняя те же действия, что и при вставке ключа:
node* remove(node* p, int k) // удаление ключа k из дерева p
{
if( !p ) return 0;
if( k < p->key )
p->left = remove(p->left,k);
else if( k > p->key )
p->right = remove(p->right,k);
Как только ключ k найден, переходим к плану Б: запоминаем корни q и r левого и правого поддеревьев узла p; удаляем узел p; если правое поддерево пустое, то возвращаем указатель на левое поддерево; если правое поддерево не пустое, то находим там минимальный элемент min, потом его извлекаем оттуда, слева к min подвешиваем q, справа — то, что получилось из r, возвращаем min после его балансировки.
else // k == p->key
{
node* q = p->left;
node* r = p->right;
delete p;
if( !r ) return q;
node* min = findmin(r);
min->right = removemin(r);
min->left = q;
return balance(min);
}
При выходе из рекурсии не забываем выполнить балансировку:
return balance(p);
}
Вот собственно и все! Поиск минимального узла и его извлечение, в принципе, можно реализовать в одной функции, при этом придется решать (не очень сложную) проблему с возвращением из функции пары указателей. Зато можно сэкономить на одном проходе по правому поддереву.
Очевидно, что операции вставки и удаления (а также более простая операция поиска) выполняются за время пропорциональное высоте дерева, т.к. в процессе выполнения этих операций производится спуск из корня к заданному узлу, и на каждом уровне выполняется некоторое фиксированное число действий. А в силу того, что АВЛ-дерево является сбалансированным, его высота зависит логарифмически от числа узлов. Таким образом, время выполнения всех трех базовых операций гарантированно логарифмически зависит от числа узлов дерева.
Всем спасибо за внимание!
Весь код
struct node // структура для представления узлов дерева
{
int key;
unsigned char height;
node* left;
node* right;
node(int k) { key = k; left = right = 0; height = 1; }
};
unsigned char height(node* p)
{
return p?p->height:0;
}
int bfactor(node* p)
{
return height(p->right)-height(p->left);
}
void fixheight(node* p)
{
unsigned char hl = height(p->left);
unsigned char hr = height(p->right);
p->height = (hl>hr?hl:hr)+1;
}
node* rotateright(node* p) // правый поворот вокруг p
{
node* q = p->left;
p->left = q->right;
q->right = p;
fixheight(p);
fixheight(q);
return q;
}
node* rotateleft(node* q) // левый поворот вокруг q
{
node* p = q->right;
q->right = p->left;
p->left = q;
fixheight(q);
fixheight(p);
return p;
}
node* balance(node* p) // балансировка узла p
{
fixheight(p);
if( bfactor(p)==2 )
{
if( bfactor(p->right) < 0 )
p->right = rotateright(p->right);
return rotateleft(p);
}
if( bfactor(p)==-2 )
{
if( bfactor(p->left) > 0 )
p->left = rotateleft(p->left);
return rotateright(p);
}
return p; // балансировка не нужна
}
node* insert(node* p, int k) // вставка ключа k в дерево с корнем p
{
if( !p ) return new node(k);
if( k<p->key )
p->left = insert(p->left,k);
else
p->right = insert(p->right,k);
return balance(p);
}
node* findmin(node* p) // поиск узла с минимальным ключом в дереве p
{
return p->left?findmin(p->left):p;
}
node* removemin(node* p) // удаление узла с минимальным ключом из дерева p
{
if( p->left==0 )
return p->right;
p->left = removemin(p->left);
return balance(p);
}
node* remove(node* p, int k) // удаление ключа k из дерева p
{
if( !p ) return 0;
if( k < p->key )
p->left = remove(p->left,k);
else if( k > p->key )
p->right = remove(p->right,k);
else // k == p->key
{
node* q = p->left;
node* r = p->right;
delete p;
if( !r ) return q;
node* min = findmin(r);
min->right = removemin(r);
min->left = q;
return balance(min);
}
return balance(p);
}
Источники
- B. Pfaff, An Introduction to Binary Search Trees and Balanced Trees — описание библиотеки libavl
- Н. Вирт, Алгоритмы и структуры данных — сбалансированные деревья по Вирту — это как раз АВЛ-деревья
- Т. Кормен и др., Алгоритмы: построение и анализ — про АВЛ-деревья говорится в упражнениях к главе про красно-черные деревья
- Д. Кнут, Искусство программирования — раздел 6.2.3 посвящен теоретическому анализу АВЛ-деревьев
















