freetonik 30 авг 2016 в 13:52

Когда «О» большое подводит

8 мин

37K

Алгоритмы*Компиляторы*Математика*Программирование*

Перевод

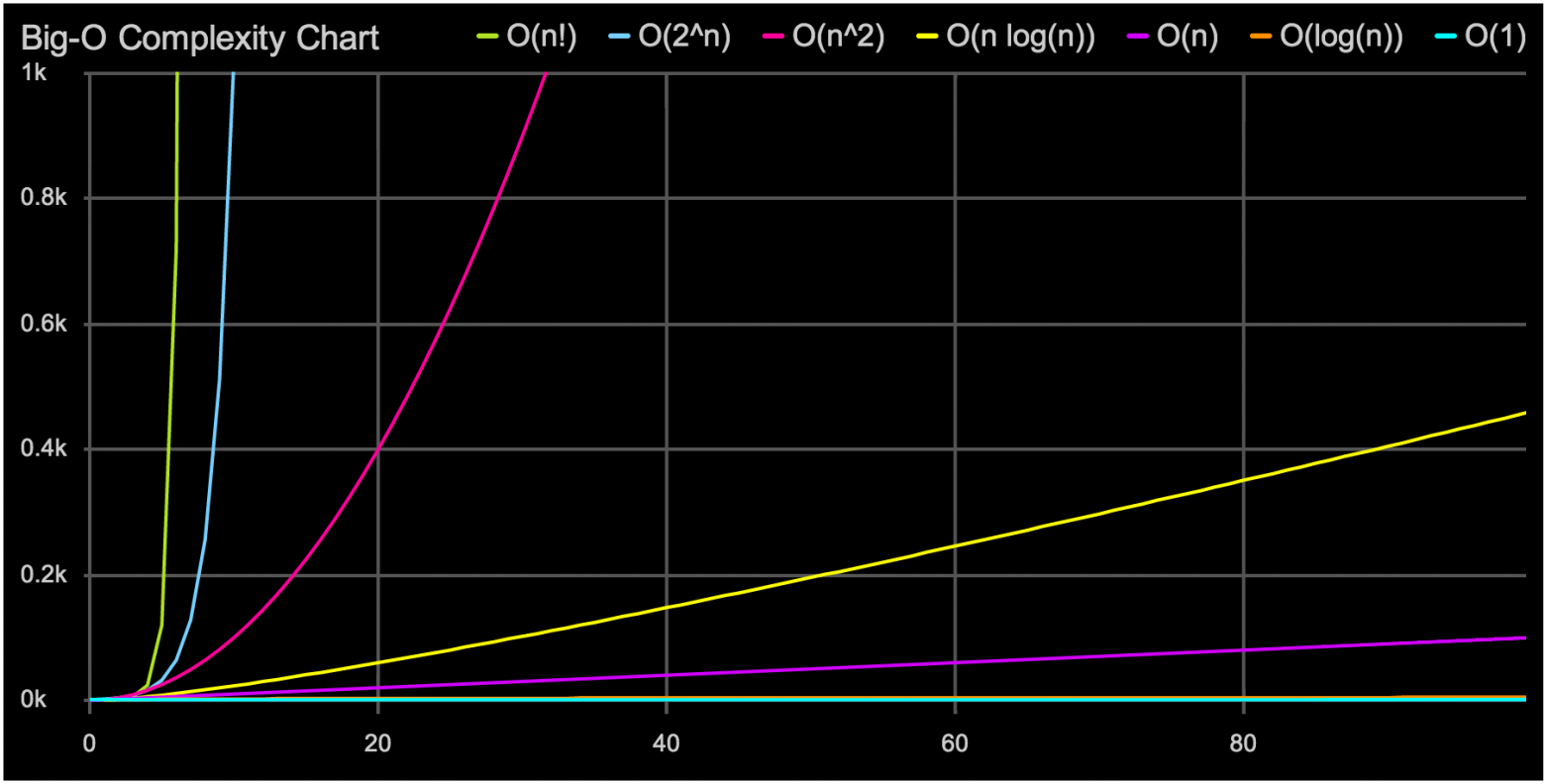
"О" большое — это отличный инструмент. Он позволяет быстро выбрать подходящую структуру данных или алгоритм. Но иногда простой анализ "О" большого может обмануть нас, если не подумать хорошенько о влиянии константных множителей. Пример, который часто встречается при программировании на современных процессорах, связан с выбором структуры данных: массив, список или дерево.

Память, медленная-медленная память

В начале 1980-х время, необходимое для получения данных из ОЗУ и время, необходимое для произведения вычислений с этими данными, были примерно одинаковым. Можно было использовать алгоритм, который случайно двигался по динамической памяти, собирая и обрабатывая данные. С тех пор процессоры стали производить вычисления в разы быстрее, от 100 до 1000 раз, чем получать данные из ОЗУ. Это значит, что пока процессор ждет данных из памяти, он простаивает сотни циклов, ничего не делая. Конечно, это было бы совсем глупо, поэтому современные процессоры содержат несколько уровней встроенного кэша. Каждый раз когда вы запрашиваете один фрагмент данных из памяти, дополнительные прилегающие фрагменты памяти будут записаны в кэш процессора. В итоге, при последовательном проходе по памяти можно получать к ней доступ почти настолько же быстро, насколько процессор может обрабатывать информацию, потому что куски памяти будут постоянно записываться в кэш L1. Если же двигаться по случайным адресам памяти, то зачастую кэш использовать не получится, и производительность может сильно пострадать. Если хотите узнать больше, то доклад Майка Актона на CppCon — это отличная отправная точка (и отлично проведенное время).

В результате этого массивы стали лучшей структурой данных, когда важна производительность, даже если согласно анализу "О" большого массив должен работать медленнее. Там, где вы хотели использовать дерево, отсортированный массив с двоичным поиском может подойти лучше. Там, где вы хотели использовать очередь, растущий массив может подойти лучше, и так далее.

Связный список и динамический массив

Когда вы поняли важность доступа к последовательной памяти, для вас не будет сюрпризом тот факт, что если нужно быстро пройти по коллекции, то массив будет быстрее связного списка. Окружения с умным управлением памятью и сборщиками мусора, возможно, будут хранить узлы связного списка более последовательно, но они не могут гарантировать это. Использование сырого массива обычно требует более сложного кода, особенно когда нужно вставлять или добавлять новые элементы, так как придется обрабатывать рост массива, перемещение элементов, и так далее. В большинстве языков есть родные библиотеки, содержащие ту или иную реализацию динамических массивов. В C++ естьvector, в C# есть List (в F# используется под именем ResizeArray), а в Java есть ArrayList. Обычно эти структуры предоставляют такой же или похожий интерфейс, как и связный список. В этой статье я буду называть такие структуры динамическими массивами (Array List), но имейте ввиду, что в примерах на C# используется класс List, а не более старый ArrayList.

Что, если нужна структура данных, в которую можно быстро вставлять элементы и быстро проходить по ним? Давайте представим, для этого примера, что у нас такой случай: мы будем вставлять в начало коллекции примерно в 5 раз чаще, чем проходить по ней. Давайте также представим, что и у связного списка, и у динамического массива в нашей среде есть одинаково приятные для работы интерфейсы. Остается только решить, что будет более эффективным решением. Мы можем обратиться к анализу "О" большго для оптимизации нашего ценного времени. Обратимся к полезной подсказке про "О" большое, соответствующие сложности для этих структур данных это:

	Проход	Вставка
Динамический массив	O(n)	O(n)
Связный список	O(n)	O(1)

Проблема динамических массивов заключается во вставке, как минимум нужно будет копировать и двигать каждый элемент на единицу после точки вставки чтобы освободить место для нового элемента. Отсюда O(n). Иногда нужно создать новый массив, больший по размеру чтобы появилось место для вставки. В нашем случае вставка происходит в 5 раз чаще, чем проход, так что, кажется, вывод очевиден. Пока n достаточно большой, связный список должен в целом быть эффективнее.

Эксперимент

Но чтобы удостовериться, лучше посчитать. Давайте проведем эксперимент с C#, используя BenchMarkDotNet. В C# есть коллекция LinkedList, которая является классическим связным списком, и List, который является динамическим массивом. Интерфейсы у обоих похожи, и оба можно с легкостью применить в нашем случае. Рассмотрим худший случай для динамического массива — вставка всегда происходит в начало, так что приходится копировать весь массив при каждой вставке. Конфигурация окружения тестирования такая:

Host Process Environment Information:
BenchmarkDotNet.Core=v0.9.9.0
OS=Microsoft Windows NT 6.2.9200.0
Processor=Intel(R) Core(TM) i7-4712HQ CPU 2.30GHz, ProcessorCount=8
Frequency=2240910 ticks, Resolution=446.2473 ns, Timer=TSC
CLR=MS.NET 4.0.30319.42000, Arch=64-bit RELEASE [RyuJIT]
GC=Concurrent Workstation
JitModules=clrjit-v4.6.1590.0

Type=Bench  Mode=Throughput

Тест-кейсы:

    [Benchmark(Baseline=true)]
    public int ArrayTest()
    {        
        //In C#, List<T> is an array backed list.
        List<int> local = arrayList;
        int localInserts = inserts;
        int sum = 0;
        for (int i = 0; i < localInserts; i++)
        {
            local.Insert(0, 1); //Insert the number 1 at the front
        }

        // For loops iterate over List<T> much faster than foreach
        for (int i = 0; i < local.Count; i++)
        {
            sum += local[i];  //do some work here so the JIT doesn't elide the loop entirely
        }
        return sum;
    }

    [Benchmark]
    public int ListTest()
    {
        LinkedList<int> local = linkedList;
        int localInserts = inserts;
        int sum = 0;
        for (int i = 0; i < localInserts; i++)
        {
            local.AddFirst(1); //Insert the number 1 at the front
        }

        // Again, iterating the fastest possible way over this collection
        var node = local.First;
        for (int i = 0; i < local.Count; i++)
        {
            sum += node.Value;
            node = node.Next;
        }

        return sum;
    }

Результаты:

Метод	Размер	Вставки	Медиана
ArrayTest	100	5	38.9983 us
ListTest	100	5	51.7538 us

Динамический массив выигрывает с неплохим отрывом. Но это маленький список, "О" большое описывает производительность только растущего до больших размеров n, так что результаты теста должны в итоге перевернуться наоборот при увеличении n. Давайте попробуем:

Метод	Размер	Вставки	Медиана
ArrayTest	100	5	38.9983 us
ListTest	100	5	51.7538 us
ArrayTest	1000	5	42.1585 us
ListTest	1000	5	49.5561 us
ArrayTest	100000	5	208.9662 us
ListTest	100000	5	312.2153 us
ArrayTest	1000000	5	2,179.2469 us
ListTest	1000000	5	4,913.3430 us
ArrayTest	10000000	5	36,103.8456 us
ListTest	10000000	5	49,395.0839 us

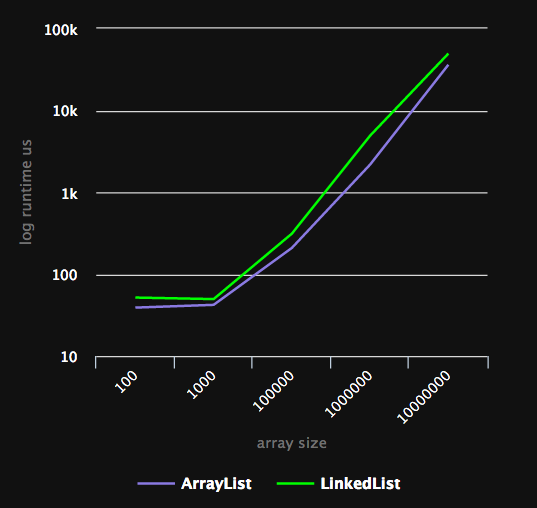
Неожиданные для многих результаты. Каким бы большим ни был n, динамический массив все равно оказывается лучше. Чтобы производительность стала хуже, отношение вставок к проходам должно измениться, а не только размер коллекции. Заметьте, что это не ошибка анализа "О" большого, это просто человеческая ошибка — мы неправильно применяем метод. Если углубиться в математику, то "О" большое покажет, что обе структуры данных будут расти с одной скоростью пока отношение вставок к проходам не меняется.

Где находится переломный момент, зависит от множества факторов, но хорошее приближенное правило предложено Чандлером Каррутом из Google: динамический массив будет эффективнее связного списка до тех пор, пока вставок не станет на порядок больше, чем проходов. В нашем случае правило работает хорошо, потому что при отношении 10:1 можно увидеть сдвиг в сторону связного списка:

Метод	Размер	Вставки	Медиана
ArrayTest	100000	10	328,147.7954 ns
ListTest	100000	10	324,349.0560 ns

Дьявол в деталях

Динамический массив побеждает потому, что числа, по которым происходит проход, находятся в памяти последовательно. Каждый раз, когда происходит запрос числа из памяти, целый набор чисел добавляется в кэш L1, так что следующие 64 байта данных уже готовы к обработке. При работе со связным списком каждый вызов node.Next перенаправляет указатель на следующий узел, и нет гарантий, что этот узел будет находится в памяти сразу за предыдущим. Поэтому иногда мы будем попадать мимо кэша. Но нам не всегда приходится работать с типами, хранящими непосредственно значения, особенно в объектно-ориентированных языках, где проход зачастую происходит по ссылочным типам. В таком случае, не смотря на то, что в динамическом массиве сами указатели находятся в памяти последовательно, объекты, на которые они указывают — нет. Ситуация все еще лучше, чем со связным списком, где вам придется дважды разыменовывать указатели для каждого элемента, но как это влияет на общую производительность?

Производительность значительно ухудшается, в зависимости от размера объектов и особенностей железа и софта. Если заменить в примере выше числа на маленькие объекты (12 байт), то точка "перелома" опускается до 4 вставок к одному проходу:

Метод	Размер	Вставки	Медиана
ArrayTestObject	100000	0	674.1864 us
ListTestObject	100000	0	1,140.9044 us
ArrayTestObject	100000	2	959.0482 us
ListTestObject	100000	2	1,121.5423 us
ArrayTestObject	100000	4	1,230.6550 us
ListTestObject	100000	4	1,142.6658 us

Управляемый код на C# сильно страдает в этом случае, потому что проход по динамическому массиву создает излишние проверки границ массива. Вектор в С++, скорее всего, будет работать эффективнее. Если быть совсем агрессивным в решении этой задачи, то можно написать более быстрый класс для динамического массива с использованием небезопасного кода C# чтобы избежать проверки границ массива. Относительная разница также будет сильно зависеть от того, как распределитель памяти и сборщик мусора управляют динамической памятью, насколько большие объекты и от других факторов. Более крупные объекты обычно улучшают производительность динамических массивов в моей среде. Когда речь идет о целых приложениях, относительная производительность динамических массивов может также улучшаться с увеличением фрагментации динамической памяти, но чтобы удостовериться, нужно проводить тестирование.

Еще один момент. Если объекты достаточно маленькие (от 16 до 32 байтов или меньше в разных ситуациях), то стоит рассмотреть вариант хранения их по значению (struct в .NET), а не в объекте. Это не только сильно улучшит производительность благодаря последовательному распределению в памяти, но также теоретически уменьшит дополнительную нагрузку из-за сборки мусора, в зависимости от сценария использования этих данных:

Метод	Размер	Вставки	Медиана
ArrayTestObject	100000	10	2,094.8273 us
ListTestObject	100000	10	1,154.3014 us
ArrayTestStruct	100000	10	792.0004 us
ListTestStruct	100000	10	1,206.0713 us

Java здесь может показать лучшие результаты, потому что она автоматически делает умные изменения маленьких объектов, или можно просто использовать отдельные массивы примитивных типов. И хотя такое писать очень нудно, это может оказаться быстрее, чем массив структур. Все зависит от особенностей обращения к данным в вашем коде. Имейте это ввиду, когда производительность особенно важна.

Убедитесь, что абстракция себя оправдывает

Часто люди не согласны с такими выводами, и их аргументы— это чистота кода, корректность и поддерживаемость. Конечно, в каждой сфере есть свои приоритеты, но я считаю, что когда абстракция лишь ненамного улучшает чистоту когда, а производительность страдает сильно, нужно взять за правило выбирать производительность. Если не жалеть времени на изучение среды, то можно узнать о случаях, когда существует более быстрое и не менее чистое решение, как это часто бывает в случае с динамическими массивами вместо списков.

Информация для размышления: вот семь разных способов найти сумму списка чисел в C#, со временем исполнения и использованием памяти. Везде используется арифметика с проверкой переполнения, чтобы сравнение с Linq, где метод Sum использует именно такую арифметику, было корректным. Заметьте, насколько лучший метод быстрее остальных. Заметьте, насколько затратный самый популярный способ. Заметьте, что абстракция foreach хорошо работает с массивами, но не с динамическими массивами или связными списками. Каким бы ни был ваш язык и окружение, важно понимать эти детали чтобы принимать правильные решения по умолчанию.

Method	Length	Median	Bytes Allocated/Op
LinkedListLinq	100000	990.7718 us	23,192.49
RawArrayLinq	100000	643.8204 us	11,856.39
LinkedListForEach	100000	489.7294 us	11,909.99
LinkedListFor	100000	299.9746 us	6,033.70
ArrayListForEach	100000	270.3873 us	6,035.88
ArrayListFor	100000	97.0850 us	1,574.32
RawArrayForEach	100000	53.0535 us	1,574.84
RawArrayFor	100000	53.1745 us	1,577.77

    [Benchmark(Baseline = true)]
    public int LinkedListLinq()
    {
        var local = linkedList;
        return local.Sum();
    }

    [Benchmark]
    public int LinkedListForEach()
    {
        var local = linkedList;
        int sum = 0;
        checked
        {
            foreach (var node in local)
            {
                sum += node;
            }
        }
        return sum;
    }

    [Benchmark]
    public int LinkedListFor()
    {
        var local = linkedList;
        int sum = 0;
        var node = local.First;
        for (int i = 0; i < local.Count; i++)
        {
            checked
            {
                sum += node.Value;
                node = node.Next;
            }
        }

        return sum;
    }

    [Benchmark]
    public int ArrayListFor()
    {
        //In C#, List<T> is an array backed list
        List<int> local = arrayList;
        int sum = 0;

        for (int i = 0; i < local.Count; i++)
        {
            checked
            {
                sum += local[i];
            }
        }

        return sum;
    }

    [Benchmark]
    public int ArrayListForEach()
    {        
        //In C#, List<T> is an array backed list
        List<int> local = arrayList;
        int sum = 0;
        checked
        {
            foreach (var x in local)
            {
                sum += x;
            }
        }
        return sum;
    }

    [Benchmark]
    public int RawArrayLinq()
    {
        int[] local = rawArray;
        return local.Sum();
    }

    [Benchmark]
    public int RawArrayForEach()
    {
        int[] local = rawArray;
        int sum = 0;
        checked
        {
            foreach (var x in local)
            {
                sum += x;
            }
        }
        return sum;
    }

    [Benchmark]
    public int RawArrayFor()
    {
        int[] local = rawArray;
        int sum = 0;

        for (int i = 0; i < local.Length; i++)
        {
            checked
            {
                sum += local[i];
            }
        }

        return sum;
    }

Теги:

Хабы: