PatientZero 29 дек 2017 в 11:31

Объёмное атмосферное рассеяние света

31 мин

29K

Алгоритмы*Работа с 3D-графикой*Разработка игр*

Перевод

Если вы прожили на планете Земля достаточно долго, то наверно задавались вопросом, почему небо обычно синее, но краснеет на закате. Оптическое явление, которое стало (основной) причиной этого, называется рэлеевским рассеянием. В этой статье я расскажу, как смоделировать атмосферное рассеяние, чтобы имитировать многие визуальные эффекты, которые проявляются на планетах. Если вы хотите научиться рендерить физически точные изображения чужих планет, то этот туториал определённо стоит изучить.

GIF

Статья разбита на следующие части:

Часть 1. Объёмное атмосферное рассеяние
Часть 2. Теория атмосферного рассеяния
Часть 3. Математика рэлеевского рассеяния
Часть 4. Путешествие сквозь атмосферу
Часть 5. Атмосферный шейдер
Часть 6. Пересечение атмосферы
Часть 7. Шейдер атмосферного рассеяния

Часть 1. Объёмное атмосферное рассеяние

Введение

Воссоздать атмосферные явления так сложно потому, что небо не является непрозрачным объектом. В традиционных техниках рендеринга предполагается, что объекты — это просто пустые оболочки. Все графические вычисления производятся на поверхностях материалов и не зависят от того, что находится внутри. Это сильное упрощение позволяет очень эффективно выполнять рендеринг непрозрачных объектов. Однако свойства некоторых материалов определяются тем, что свет может проходить сквозь них. Конечный внешний вид просвечивающих объектов становится результатом взаимодействия света с их внутренней структурой. В большинстве случаев такое взаимодействие можно очень эффективно имитировать, как это можно увидеть в туториале "Быстрый шейдер для Subsurface Scattering в Unity". К сожалению, в нашем случае, если мы хотим создать убедительное небо, это не так. Вместо рендеринга только «внешней оболочки» планеты нам придётся симулировать то, что происходит с лучами света, проходящими сквозь атмосферу. Выполнение вычислений внутри объекта называется объёмным рендерингом; эту тему мы подробно рассматривали в серии статей Volumetric Rendering. В этой серии статей я рассказал о двух техниках (raymarching и знаковых функциях расстояния), которые невозможно эффективно использовать для симуляции атмосферного рассеяния. В этой статье мы познакомимся с более подходящей для рендеринга просвечивающих твёрдых объектов техникой, часто называемой единичным объёмным рассеянием.

Единичное рассеяние

В комнате без света мы ничего не увидим. Объекты становятся видимыми, только когда от них отражаются лучи света и попадают в наш глаз. В большинстве игровых движков (таких как Unity и Unreal) предполагается, что свет движется в «вакууме». Это значит, что на свет могут влиять только объекты. На самом же деле, свет всегда движется в среде. В нашем случае такой средой является вдыхаемый нами воздух. Поэтому на внешний вид объекта влияет расстояние, проходимое светом в воздухе. На поверхности Земли плотность воздуха относительно мала, её влияние настолько незначительно, что её стоит учитывать только когда свет проходит большие расстояния. Далёкие горы сливаются с небом, однако на близкие объекты атмосферное рассеяние почти не влияет.

Первым шагом в воссоздании оптического эффекта атмосферного рассеяния будет анализ того, как свет проходит через такие среды, как воздух. Как сказано выше, мы можем увидеть предмет только тогда, когда свет падает в наш глаз. В контексте 3D-графики нашим глазом является камера, используемая для рендеринга сцены. Молекулы, из которых состоит воздух вокруг нас, могут отражать проходящие через них световые лучи. Поэтому они способны менять то, как мы воспринимаем объекты. Если сильно упростить, то существует два способа, которыми молекулы могут повлиять на наше зрение.

Рассеяние наружу

Наиболее очевидный способ взаимодействия молекул со светом заключается в том, что они отражают свет, меняя его направление. Если направленный в камеру луч света отражается, то мы наблюдаем процесс рассеяния наружу.

Реальный источник света может испускать каждую секунду квадрильоны фотонов, и каждый из них с определённой вероятностью может столкнуться с молекулой воздуха. Чем плотнее среда, в которой движется свет, тем вероятнее отражение единичного фотона. Влияние рассеяния наружу также зависит от пройденного светом расстояния.

Рассеяние наружу приводит к тому, что свет постепенно становится всё более тусклым, и это свойство зависит от пройденного расстояния и плотности воздуха.

Рассеяние внутрь

Когда свет отражается частицей, то может случиться так, что он перенаправляется в камеру. Такой эффект противоположен рассеянию наружу, и логично, что он называется рассеянием внутрь.

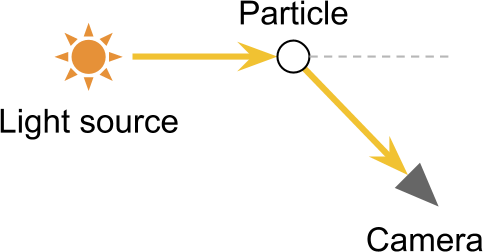
При определённых условиях рассеяние внутрь позволяет увидеть источники света, не находящиеся в прямой области видимости камеры. Наиболее очевидным результатом этого является оптический эффект — световые гало вокруг источников света. Они возникают из-за того, что камера получает из одного источника и прямые, и непрямые лучи света, что де-факто увеличивает количество получаемых фотонов.

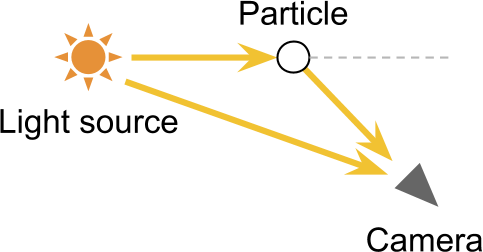
Единичное объёмное рассеяние

Один луч света может отражаться произвольное число раз. Это значит, что прежде чем попасть в камеру. луч может проходить очень сложными маршрутами. Это становится для нас серьёзной сложностью, потому что рендеринг просвечивающих материалов с высоким качеством требует симуляции путей каждого из отдельных лучей света. Эта техника называется трассировкой лучей (raytracing), и в настоящее время она слишком затратна для реализации в реальном времени. Представленная в этом туториале техника единичного рассеяния учитывает единственное событие рассеяния луча света. Позже мы увидим, что такое упрощение всё равно позволяет получать реалистичные результаты всего за небольшую долю расчётов, необходимых для настоящей трассировки лучей.

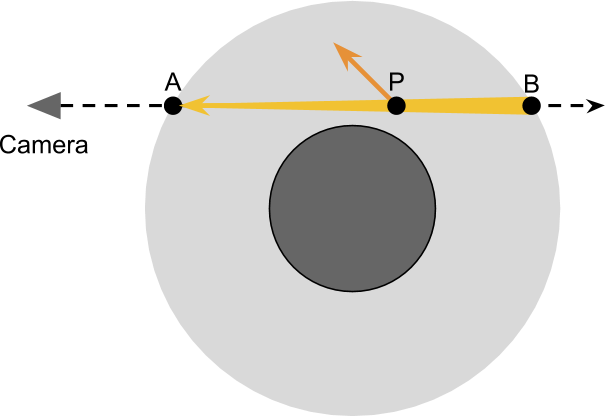
Основой рендеринга реалистичного неба является симуляция того, что происходит с лучами света при прохождении сквозь атмосферу планеты. На схеме ниже показана камера, смотрящая сквозь планету. Основная идея этой техники рендеринга заключается в вычислении того, как на прохождение света из $inline$ в $inline$ влияет рассеяние. Это означает, что нужно вычислить влияние, которое имеет рассеяние внутрь и наружу на луч, проходящий к камере. Как сказано выше, из-за рассеяния наружу мы наблюдаем затухание. Количество света, присутствующее в каждой точке $P \in \overline{AB}$ имеет небольшую вероятность отражения в сторону от камеры.

Чтобы корректно учитывать величину рассеяния наружу, происходящего в каждой точке $inline$ , нам сначала нужно узнать, какое количество света присутствовало в $inline$ . Если считать, что планету освещает только одна звезда, то весь свет, получаемый $inline$ , должен поступать от солнца. Часть этого света будет подвержена рассеянию внутрь и отразится в камеру:

Этих двух этапов достаточно для аппроксимации большинства эффектов, наблюдаемых в атмосфере. Однако всё усложняется тем, что количество света, получаемого $inline$ от солнца, тоже подвержено рассеянию наружу, когда свет проходит через атмосферу из $inline$ в $inline$ .

Подведём итог тому, что нам нужно сделать:

Область видимости камеры входит в атмосферу в $inline$ и находится в $inline$ ;
В качестве аппроксимации мы будем учитывать влияние рассеяния внутрь и наружу, когда оно происходит в каждой точке $P \in \overline{AB}$ ;
Величина света, получаемого $inline$ от солнца;
Величина света, получаемого $inline$ и подверженного рассеянию наружу при прохождении через атмосферу $\overline{CP}$ ;
Часть света, получаемая $inline$ и подверженная рассеянию внутрь, которое перенаправляет лучи в камеру;
Часть света из $inline$ , направляемая в камеру, подвергается рассеянию наружу и отражается от области видимости.

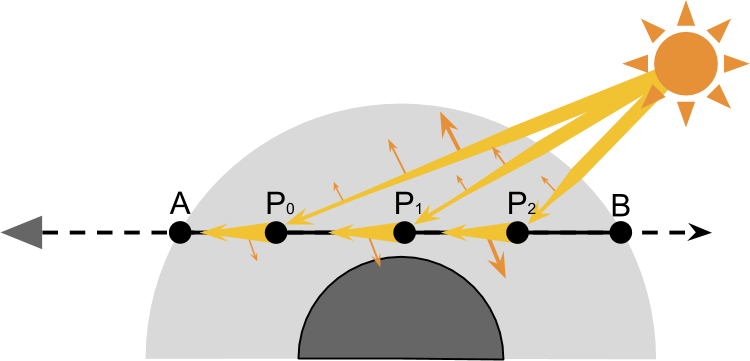
Это не единственный способ, которым лучи света могут попасть в камеру!

Предложенное в этом туториале решение учитывает рассеяние внутрь вдоль области видимости $\overline{AB}$ . Свет, достигающий точки $inline$ от солнца, с определённой вероятностью может отразиться в камеру.

Однако существует множество путей, по которым лучи могут попасть в камеру. Например, один из лучей, рассеянный наружу на пути к $inline$ , при втором столкновении может рассеяться обратно, по направлению к камере (см. схему ниже). И могут существовать лучи, достигающие камеры после трёх отражений, или даже четырёх.

Рассматриваемая нами техника называется единичным рассеянием, потому что учитывает только рассеяние внутрь, происходящее вдоль области видимости. Более сложные техники могут расширить этот процесс и учитывать другие способы, которыми луч может достичь камеры. Однако количество возможных путей растёт с увеличением количества рассматриваемых событий рассеяния экспоненциально. К счастью, вероятность попадания в камеру тоже уменьшается экспоненциально.

Часть 2. Теория атмосферного рассеяния

В этой части мы начнём выводить уравнения, управляющие этим сложным, но прекрасным оптическим явлением.

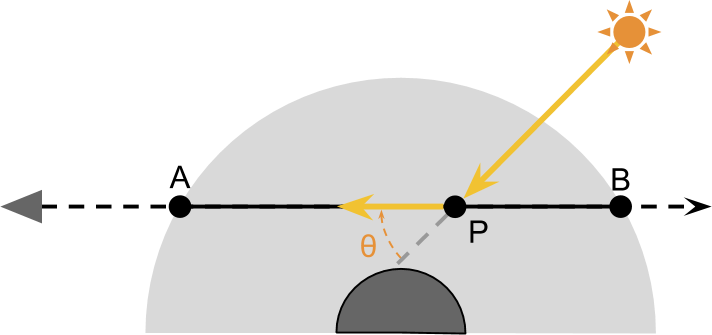
Функция пропускания

Для вычисления величины света, пропускаемого к камере, полезно совершить то же путешествие, которое проходят лучи от солнца. Посмотрев на схему ниже, легко увидеть, что лучи света, достигающие $inline$ , проходят через пустое пространство. Поскольку на их пути ничего нет, весь свет достигает $inline$ , не подвергаясь никакому эффекту рассеяния. Давайте обозначим переменной $inline$ количество нерассеянного света, получаемого точкой $inline$ от солнца. Во время своего путешествия к $inline$ , луч входит в атмосферу планеты. Некоторые лучи сталкиваются с висящими в воздухе молекулами и отражаются в разные стороны. В результате часть света рассеивается с пути. Количество света, достигающего $inline$ (обозначенное как $inline$ ), будет меньше, чем $inline$ .

Соотношение $inline$ и $inline$ называется пропусканием:

$T\left(\overline{CP}\right) = \frac{I_P}{I_C}$

Мы можем использовать его для обозначения процента света, который не был рассеян (то есть был пропущен) при путешествии от $inline$ до $inline$ . Позже мы исследуем природу этой функции. Пока единственное, что нам нужно знать — оно соответствует влиянию атмосферного рассеяния наружу.

Следовательно, количество света, получаемого $inline$ , равно:

$I_P = I_C \, T\left(\overline{CP}\right)$

Функция рассеяния

Точка $inline$ получает свет непосредственно от солнца. Однако не весь этот свет, проходящий через $inline$ , передаётся обратно в камеру. Чтобы вычислить количество света, на самом деле достигающее камеры, мы введём новую концепцию: функцию рассеяния $inline$ . Она будет обозначать количество света, отражённого в определённом направлении. Если мы посмотрим на схему ниже, то увидим, что к камере будут направлены только лучи, отражённые на угол $\theta$ .

Значение $S\left(\lambda, \theta, h\right)$ обозначает долю света, отражённого на $\theta$ радиан. Эта функция — основная наша проблема, и мы исследуем её природу в следующей части. Пока единственное, что нужно знать — что она зависит от цвета получаемого света (определяемого длиной волны $\lambda$ ), угла рассеяния $\theta$ и высоты $inline$ точки $inline$ . Высота важна потому, что плотность атмосферы изменяется как функция от высоты. А плотность является одним из факторов, определяющих количество рассеиваемого света.

Теперь у нас есть все необходимые инструменты для записи общего уравнения, показывающего количество света, переданного от $inline$ к $inline$ :

$I_{PA} = \boxed{I_P} \, S\left(\lambda,\theta,h\right) \, T\left(\overline{PA}\right)$

Благодаря предыдущему определению мы можем развернуть $inline$ :

$I_{PA} = \boxed{I_C \, T\left(\overline{CP}\right)}\, S\left(\lambda,\theta,h\right) \,T\left(\overline{PA}\right)=$

$=\underset{\text{in-scattering}}{ \underbrace{I_C \,S\left(\lambda,\theta,h\right)} }\, \underset{\text{out-scattering}}{\underbrace{T\left(\overline{CP}\right)\, T\left(\overline{PA}\right)}}$

Уравнение говорит само за себя:

Свет проходит от солнца к $inline$ , не рассеиваясь в вакууме космоса;
Свет входит в атмосферу и проходит от $inline$ к $inline$ . В этом процессе из-за рассеяния наружу только часть $T\left(\overline{CP}\right)$ достигает точки назначения;
Часть света, который добрался от солнца до $inline$ , отражается назад в камеру. Доля света, подверженного рассеянию внутрь равна $S\left(\lambda,\theta,h\right)$ ;
Оставшийся свет проходит от $inline$ до $inline$ , и снова проспускается только часть $T\left(\overline{PA}\right)$ .

Численное интегрирование

Если вы внимательно прочитали предыдущие параграфы, то могли заметить, что яркость записывалась по-разному. Символ $I_{PA}$ обозначает количество света, переданного от $inline$ к $inline$ . Однако величина не учитывает весь свет, который получает $inline$ . В этих упрощённых моделях атмосферного рассеяния мы учитываем рассеяние внутрь от каждой точки вдоль области видимости камеры в атмосфере.

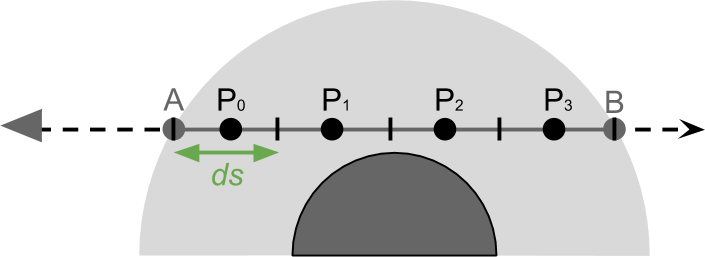
Общее количество света, получаемого $inline$ ( $inline$ ), вычисляется сложением влияния всех точек $P \in \overline{AB}$ . С точки зрения математики, на отрезке $\overline{AB}$ есть бесконечное множество точек, поэтому циклический обход их всех невозможен. Однако мы можем разделить $\overline{AB}$ на меньшие отрезки длины $inline$ (см. схему ниже), и суммировать влияние каждого из них.

Такой процесс аппроксимации называется численным интегрированием и приводит к следующему выражению:

$I_A = \sum_{P \in \overline{AB}} {I_{PA}\, ds }$

Чем больше точек мы учитываем, тем точнее будет конечный результат. В реальности же в нашем атмосферном шейдере мы просто циклически обойдём несколько точек $inline$ внутри атмосферы, суммируя их влияние в общий результат.

Почему мы умножаем на ds?

Здесь мы используем аппроксимацию непрерывного явления. Чем больше точек мы рассмотрим, тем ближе будем к реальному результату. Умножая каждую точку на $inline$ , мы придаём её влиянию вес согласно её длине. Чем больше точек у нас есть, тем менее важна каждая из них.

Можно посмотреть на это и иначе: умножая на $inline$ , мы «усредняем» влияние всех точек.

Направленное освещение

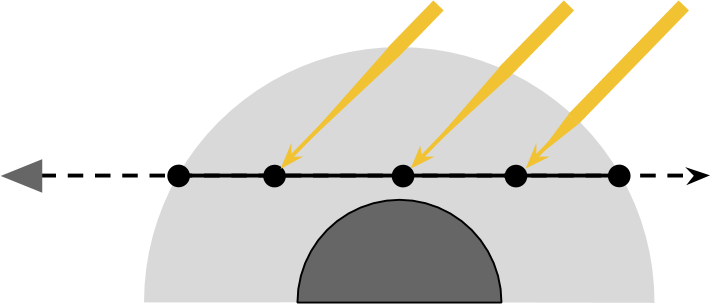
Если солнце относительно близко, то его лучше всего моделировать как точечный источник света. В этом случае количество полученного $inline$ света зависит от расстояния до солнца. Однако если мы говорим о планетах, то часто предполагаем, что солнце находится так далеко, что его лучи падают на планету под одним углом. Если это справедливо, то мы можем моделировать солнце как направленный источник света. Свет, получаемый от направленного источника света, остаётся постоянным, вне зависимости от пройденного им расстояния. Поэтому каждая точка $inline$ получает одинаковое количество света, а направление относительно солнца одинаково для всех точек.

Мы можем использовать это допущение, чтобы упростить наши уравнения.

Давайте заменим $inline$ константой $inline$ , которая определяет яркость солнца.

$I_A = \sum_{P \in \overline{AB}} {\boxed{I_{PA}}\, ds } =$

$= \sum_{P \in \overline{AB}} {\boxed{I_C \,S\left(\lambda,\theta,h\right) \,T\left(\overline{CP}\right)\, T\left(\overline{PA}\right)}\, ds }=$

$= I_S \sum_{P \in \overline{AB}} {S\left(\lambda,\theta,h\right) \,T\left(\overline{CP}\right) \, T\left(\overline{PA}\right) \,ds }=$

Есть ещё одна оптимизация, которую мы можем выполнить, она включает в себя функцию рассеяния $S\left(\lambda,\theta,h\right)$ . Если солнечный свет всегда падает с одного направления, то угол $\theta$ становится постоянным. Ниже мы увидим, что из суммы можно исключить направленное влияние $S\left(\lambda,\theta,h\right)$ . Но пока мы его оставим.

Коэффициент поглощения

При описании возможных результатов взаимодействия между светом и молекулами воздуха, мы допустили всего два варианта — или прохождение насквозь, или отражение. Но существует и третья возможность. Некоторые химические соединения поглощают свет. В атмосфере Земли есть множество веществ, обладающих таким свойством. Озон, например, находится в верхних слоях атмосферы и активно взаимодействует с ультрафиолетовым излучением. Однако его присутствие не оказывает практически никакого воздействия на цвет неба, потому что он поглощает свет за пределами видимого спектра. Здесь, на Земле, влияние светопоглощающих веществ часто игнорируется. Но в случае других планет от него отказаться нельзя. Например, обычная окраска Нептуна и Урана вызвана присутствием большого количества метана в их атмосфере. Метан поглощает красный свет, что даёт синий оттенок. В оставшейся части туториала мы будем игнорировать коэффициент поглощения, однако добавим способ «подкрашивания» атмосферы.

Почему Солнце стало красным во время урагана Офелия 2017 года?

Если вы живёте в Великобритании, то могли заметить, что во время урагана Офелия солнце становилось красным. Так происходило потому, что Офелия принесла песок из Сахары. Эти крошечные частицы, висевшие в воздухе, усиливали эффект рассеяния. Как мы увидим в следующей части, синий свет рассеивается сильнее, чем красный.

Если посмотреть на цвета видимого спектра (ниже), то легко увидеть, что если рассеивается достаточное количество синего света, то небо и в самом деле может стать жёлтым или красным.

Есть искушение сказать, что цвет окраски неба связан с оттенком жёлтого сахарского песка. Однако такой же эффект можно увидеть во время больших пожаров из-за частиц дыма, которые обычно близки к чёрному цвету.

Часть 3. Математика рэлеевского рассеяния.

В этой части мы познакомимся с математикой рэлеевского рассеяния — оптического явления, из-за которого небо выглядит голубым. Выведенные в этой части уравнения мы перенесём в код шейдера следующей части.

Введение

В предыдущей части мы вывели уравнение, представляющее собой хорошую основу для аппроксимации атмосферного рассеяния в шейдере. Однако мы упустили то, что одно уравнение не даст нам убедительных результатов. Если нам нужен красиво выглядящий атмосферный шейдер, то нужно немного углубиться в математику.

Взаимодействие между светом и материей невероятно сложно, и нам не удастся полностью описать его лёгким способом. На самом деле, моделирование атмосферного рассеяния очень трудоёмко. Часть проблемы вызвана тем, что атмосфера не является однородной средой. Её плотность и состав значительно меняются как функция от высоты, что делает практически невозможным создание «идеальной» модели.

Именно поэтому в научной литературе приводится несколько моделей рассеяния, каждая из которых предназначена для описания подмножества оптических явлений, возникающих при определённых условиях. Большинство оптических эффектов, демонстрируемых планетами, можно воссоздать, учитывая всего две разные модели: рэлеевского рассеяния и рассеяния света сферической частицей. Эти два математических инструмента позволяют прогнозировать рассеяния света на объектах различного размера. Первая моделирует отражение света молекулами кислорода и азота, составляющими бОльшую часть состава воздуха. Последняя моделирует отражение света в более крупных структурах, присутствующих в нижних слоях атмосферы, таких как пыльца, пыль и загрязнители.

Рэлеевское рассеяние является причиной голубого неба и красных закатов. Рассеяние света сферической частицей придаёт облакам их белый цвет. Если вы хотите знать, как это происходит, то нам придётся глубже погрузиться в математику рассеяния.

Рэлеевское рассеяние

Какова судьба фотона, ударяющегося о частицу? Чтобы ответить на этот вопрос, нам нужно перефразировать его более формально. Представим, что луч света проходит сквозь пустое пространство и внезапно сталкивается с частицей. Результат такого столкновения сильно зависит от размера частицы и цвета светового луча. Если частица достаточно мала (размером с атомы или молекулы), то поведение света лучше прогнозируется с помощью рэлеевского рассеяния.

Что же происходит? Часть света продолжает свой путь, «не ощутив» никакого влияния. Однако небольшой процент этого исходного света взаимодействует с частицей и рассеивается во всех направлениях. Однако не все направления получают одинаковое количество света. Фотоны с большей вероятностью проходят прямо через частицу или отражаются назад. То есть вариант отражения фотона на 90 градусов менее велик. Такое поведение можно увидеть на схеме ниже. Голубой линией показаны наиболее вероятные направления рассеянного света.

Это оптическое явление математически описывается уравнением рэлеевского рассеяния $S \left(\lambda, \theta, h \right )$ , которое даёт нам долю исходного света $inline$ , отражённую в направлении $\theta$ :

$I = I_0 \, S \left(\lambda, \theta, h\right)$

$S \left(\lambda, \theta, h\right ) = \frac{\pi^2 \left(n^2-1 \right )^2}{2} \underset{\text{density}}{\underbrace{\frac{\rho\left(h\right)}{N}}} \overset{\text{wavelength}}{\overbrace{\frac{1}{\lambda^4}}} \underset{\text{geometry}}{\underbrace{\left(1+\cos^2\theta \right )}}$

Где:

$\lambda$ : длина волны (wavelength) приходящего света;
$\theta$ : угол рассеияния (scattering angle);
$inline$ : высота (altitude) точки;
$inline$ : коэффициент преломления воздуха;
$N=2.504 \cdot 10^{25}$ : количество молекул на кубический метр стандартной атмосферы;
$\rho\left(h\right)$ : коэффициент плотности.Это число на уровне моря равно $inline$ , и экспоненциально уменьшается с увеличением $inline$ . Об этой функции можно многое сказать, и мы рассмотрим её в следующих частях.

Но это не уравнение рэлеевского рассеяния!

Если вы встречались с рэлеевским рассеянием не в области компьютерной графики, то есть вероятность, что вы видели другое уравнение. Например, представленное в статье «Рэлеевское рассеяни» на Википедии, сильное отличается.

Использованное в этом туториале уравнение взято из научной статьи Display of The Earth Taking into Account Atmospheric Scattering, Нишиты et al.

Откуда взялась эта функция?

Одна из задач этого блога — объяснение вывода всех получаемых величин. К сожалению, это не относится к рэлеевскому рассеянию.

Если вам всё-таки интересно разобраться, почему частицы света так странно отражаются от молекул воздуха, то интуитивное понимание происходящего может дать следующее объяснение.

Причиной рэлеевского рассеяния на самом деле является не «отталкивание» частиц. Свет — это электромагнитная волна, и она может взаимодействовать с неравновесием зарядов, присутствующим в определённых молекулах. Эти заряды насыщаются поглощением получаемого электромагнитного излучения, которое позже испускается снова. Показанная в угловой функции двудольная форма показывает, как молекулы воздуха становятся электрическими диполями, излучающими подобно микроскопическим антеннам.

Первое, что можно заметить в рэлеевском рассеянии — это то, что в некоторых направлениях распространяется больше света, чем в других. Второй важный аспект заключается в том, что количество рассеянного света сильно зависит от длины волны $\lambda$ приходящего света. Показанная ниже круговая диаграмма визуализирует $S \left(\lambda, \theta, 0\right )$ для трёх разных длин волн. Вычисление $inline$ при $inline$ часто называется рассеянием на уровне моря.

На рисунке ниже показана визуализация коэффициентов рассеяния для непрерывного диапазона длин волн/цветов видимого спектра (код доступен в ShaderToy).

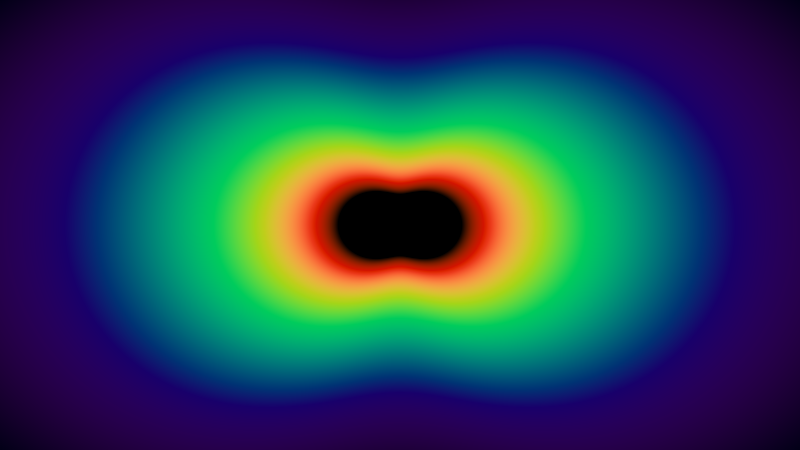
Центр изображения выглядит чёрным, потому что длины волн в этом диапазоне находятся за пределами видимого спектра.

Коэффициент рэлеевского рассеяния

Уравнение рэлеевского рассеяния показывает, какое количество света рассеивается в определённом направлении. Однако оно не говорит нам, сколько энергии всего рассеялось. Для вычисления этого нам нужно учесть рассеивание энергии во всех направлениях. Вывод уравнения нелёгок; если вы не освоили сложный матанализ, то вот результат:

$\beta \left(\lambda, h \right )=\frac{8\pi^3 \left(n^2-1 \right )^2}{3} \frac{\rho\left(h\right)}{N} \frac{1}{\lambda^4}$

Где $\beta \left(\lambda, h \right )$ показывает долю энергии, которая теряется из-за рассеяния после столкновения с одной частицей. Часто эту величину называют коэффициентом рэлеевского рассеяния.

Если вы читали предыдущую часть туториала, то можете догадаться, что $\beta$ на самом деле является коэффициентом затухания, который использовался в определении пропускания $T\left(\overline{AB}\right)$ на отрезке $\overline{AB}$ .

К сожалению, вычисление $\beta$ очень затратно. В шейдере, который мы собираемся написать, я постараюсь экономить как можно больше вычислений. По этой причине полезно будет «извлечь» из коэффициента рассеяния все множители, которые являются константами. Что даёт нам $\beta \left(\lambda\right )$ , который называется коэффициентом рэлеевского рассеяния на уровне моря ( $inline$ ):

$\beta \left(\lambda \right )=\frac{8\pi^3 \left(n^2-1 \right )^2}{3} \frac{1}{N} \frac{1}{\lambda^4}$

Покажите мне вычисления!

Уравнение рэлеевского рассеяния показывает нам долю энергии, рассеиваемой в определённом направлении. Чтобы вычислить полные потери, нам нужно учитывать все возможные направления. Для суммирования на непрерывном интервале требуется интегрирование.

Можно попробовать проинтегрировать $S \left(\lambda, \theta, h\right )$ по $\theta$ на интервале $\left[0,2\pi\right]$ , но это будет ошибкой.

Несмотря на то, что мы визуализировали рэлеевское рассеяние в двух измерениях, на самом деле это трёхмерное явление. Угол рассеяния $\theta$ может принимать любое направление в 3D-пространстве. Вычисления с учётом полного распределения функции, которое зависит от $\theta$ в трёхмерном пространстве (как $inline$ ) называется интегрированием по телесному углу:

$\beta \left(\lambda, h \right ) = \int_{0}^{2\pi} \int_{0}^{\pi} S \left(\lambda, \theta, h \right ) \sin\theta \, d\theta d\phi$

Внутренний интеграл перемещает $\theta$ в плоскости XY, а внешний — поворачивает результат вокруг оси X, чтобы учесть третье измерение. Прибавляемый $\sin \theta$ используется для сферических углов.

Процесс интегрирования интересует только то, что зависит от $\theta$ . Несколько членов $S \left(\lambda, \theta, h \right )$ постоянны, поэтому их можно перенести из под знака интеграла:

$\beta \left(\lambda, h \right )=\int_{0}^{2\pi} \int_{0}^{\pi} \underset{\text{constant}}{\underbrace{ \frac{\pi^2 \left(n^2-1 \right )^2}{2} \frac{\rho\left(h\right)}{N} \frac{1}{\lambda^4} }} \left(1+\cos^2\theta \right ) \sin\theta \, d\theta d\phi=$

$=\frac{\pi^2 \left(n^2-1 \right )^2}{2} \frac{\rho\left(h\right)}{N} \frac{1}{\lambda^4} \int_{0}^{2\pi} \int_{0}^{\pi} \left(1+\cos^2\theta \right ) \sin\theta \, d\theta d\phi$

Это значительно упрощает внутренний интеграл, который теперь принимает следующий вид:

$\beta \left(\lambda, h \right )=\frac{\pi^2 \left(n^2-1 \right )^2}{2} \frac{\rho\left(h\right)}{N} \frac{1}{\lambda^4} \int_{0}^{2\pi} \boxed{ \int_{0}^{\pi} \left(1+\cos^2\theta \right ) \sin\theta \, d\theta }d\phi=$

$=\frac{\pi^2 \left(n^2-1 \right )^2}{2} \frac{\rho\left(h\right)}{N} \frac{1}{\lambda^4} \int_{0}^{2\pi} \boxed{\frac{8}{3}} d\phi$

Теперь мы можем выполнить внешнее интегрирование:

$\beta \left(\lambda, h \right )=\frac{\pi^2 \left(n^2-1 \right )^2}{2} \frac{\rho\left(h\right)}{N} \frac{1}{\lambda^4} \boxed{ \int_{0}^{2\pi} \frac{8}{3} d\phi}=$

$=\frac{\pi^2 \left(n^2-1 \right )^2}{2} \frac{\rho\left(h\right)}{N} \frac{1}{\lambda^4} \boxed{ \frac{16 \pi}{3}}$

Что приводит нас к окончательному виду:

$\beta \left(\lambda, h \right )=\frac{8\pi^3 \left(n^2-1 \right )^2}{3} \frac{\rho\left(h\right)}{N} \frac{1}{\lambda^4}$

Поскольку это интеграл, учитывающий влияние рассеивания во всех направлениях, логично, что выражение больше не зависит от $\theta$ .

Это новое уравнение даёт нам ещё один способ понимания того, как рассеиваются разные цвета. На графике ниже показано количество рассеяния, которому подвержен свет, как функция от длины его волны.

Это сильная связь между коэффициентом рассеяния $\beta$ и $\lambda$ , которая становится причиной красного неба на закате. Получаемые от солнца фотоны распределяются по более широкому диапазону длин волн. Рэлеевское рассеяние говорит нам, что атомы и молекулы атмосферы Земли сильнее рассеивают синий цвет, чем зелёный или красный. Если свет сможет двигаться достаточно долго, то вся его синяя составляющая будет потеряна из-за рассеяния. Именно это происходит на закате, когда свет проходит практически параллельно поверхности.

Рассуждая так же, мы можем понять, почему небо выглядит голубым. Свет солнца падает из одного направления. Однако его синяя составляющая рассеивается во всех направлениях. Когда мы смотрим на небо, синий свет приходит со всех направлений.

Фазовая функция Рэлея

Исходное уравнение, описывающее рэлеевское рассеяние, $S \left(\lambda, \theta\right )$ , можно разложить на два компонента. Первый — это коэффициент рассеяния, который мы только что вывели, $\beta \left(\lambda\right )$ , который модулирует его интенсивность. Вторая часть связана с геометрией рассеяния, и управляет его направлением:

$S \left(\lambda, \theta, h\right ) = \beta \left(\lambda, h\right ) \gamma \left(\theta\right)$

Эту новую величину $\gamma \left(\theta\right)$ можно получить, поделив $S \left(\lambda, \theta, h\right )$ на $\beta \left(\lambda\right )$ :

$\gamma \left(\theta\right) = \frac{S \left(\lambda, \theta, h\right )} {\beta \left(\lambda\right )}=$

$= \underset{S \left(\lambda, \theta, h\right )}{\underbrace{ \frac{\pi^2 \left(n^2-1 \right )^2}{2} \frac{\rho\left(h\right)}{N} \frac{1}{\lambda^4} \left(1+\cos^2\theta \right ) }} \, \underset{\frac{1}{\beta \left(\lambda\right )}}{\underbrace{ \frac{3}{8\pi^3 \left(n^2-1 \right )^2} \frac{N}{\rho\left(h\right)} \lambda^4 }}=$

$= \frac{3}{16\pi} \left(1+\cos^2 \theta\right)$

Можно увидеть, что это новое выражение не зависит от длины волны приходящего света. Это кажется контринтуитивным, потому что мы точно знаем, что рэлеевское рассеяние сильнее воздействует на короткие волны.

Однако $\gamma \left(\theta\right)$ моделирует форму диполя, который мы видели выше. Член $\frac{3}{16\pi}$ служит коэффициентом нормализации, чтобы интеграл по всем возможным углам $\theta$ суммировался в $inline$ . Если формулировать технически, то можно сказать, что интеграл по $4\pi$ стерадианам равен $inline$ .

В следующих частях мы увидим, как разделение этих двух компонентов позволит нам вывести более эффективные уравнения.

Подведём краткий итог

Уравнение рэлеевского рассеяния: обозначает долю света, отражаемого в направлении $\theta$ . Величина рассеяния зависит от длины волны $\lambda$ поступающего света.

$S \left(\lambda, \theta, h\right ) = \frac{\pi^2 \left(n^2-1 \right )^2}{2} \frac{\rho\left(h\right)}{N} \frac{1}{\lambda^4} \left(1+\cos^2\theta \right )$

Кроме того:

$S \left(\lambda, \theta, h\right ) = \beta \left(\lambda,h \right ) \gamma\left(\theta\right)$

Коэффициент рэлеевского рассеяния: обозначает долю света, теряемую из-за рассеяния после первого столкновения.

$\beta \left(\lambda,h \right )=\frac{8\pi^3 \left(n^2-1 \right )^2}{3} \frac{\rho\left(h\right)}{N} \frac{1}{\lambda^4}$

Коэффициент рэлеевского рассеяния на уровне моря: это аналог $\beta \left(\lambda,0\right )$ . Создание этого дополнительного коэффициента будет очень полезно для выведения более эффективных уравнений.

$\beta \left(\lambda \right )=\beta \left(\lambda,0 \right )=\frac{8\pi^3 \left(n^2-1 \right )^2}{3} \frac{1}{N} \frac{1}{\lambda^4}$

Если мы рассмотрим длины волн, примерно соответствующие красному, зелёному и синему цветам, то получим следующие результаты:

$\beta\left(680nm\right) = 0.00000519673$

$\beta\left(550nm\right) = 0.0000121427$

$\beta\left(440nm\right) = 0.0000296453$

Эти результаты вычисляются при предположении, что $inline$ (это подразумевает, что $\rho=1$ ). Такое бывает только на уровне моря, где коэффициент рассеяния имеет максимальное значение. Поэтому он служит «ориентиром» величины рассеяния света.

Фазовая функция Рэлея: управляет геометрией рассеяния, которая обозначает относительную долю света, утерянного в конкретном направлении. Коэффициент $\frac{3}{16\pi}$ служит коэффициентом нормализации, поэтому интегралом по единичной сфере будет $inline$ .

$\gamma\left(\theta\right)= \frac{3}{16\pi} \left(1+\cos^2 \theta\right)$

Коэффициент плотности: эта функция используется для моделирования плотности атмосферы. Её формальное определение будет представлено ниже. Если вы не против математических спойлеров, то она определяется так:

$\rho\left(h\right)=exp\left\{-\frac{h}{H}\right\}$

где $inline$ метров называется приведённой высотой.

Часть 4. Путешествие сквозь атмосферу.

В этой части мы рассмотрим моделирование плотности атмосферы на разных высотах. Это необходимый шаг, потому что плотность атмосферы — это один из параметров, нужных для корректного вычисления рэлеевского рассеяния.

Коэффициент плотности атмосферы

До сих пор мы не рассматривали роль коэффициента плотности атмосферы $\rho$ . Логично, что сила рассеяния пропорциональна плотности атмосферы. Чем больше молекул на кубический метр, тем больше вероятность рассеяния фотонов. Сложность заключается в том, что структура атмосферы очень сложна, она состоит из нескольких слоёв с разным давлением, плотностью и температурой. К счастью для нас, основная часть рэлеевского рассеяния происходит в первых 60 км атмосферы. В тропосфере температура снижается линейно, а давление снижается экспоненциально.

На схеме ниже показана связь между плотностью и высотой в нижних слоях атмосферы.

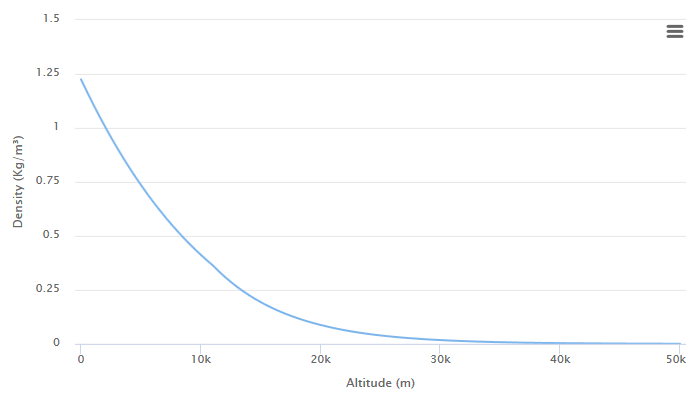
Значение $\rho \left(h\right)$ представляет собой замер атмосферы на высоте $inline$ метров, нормализованный таким образом, что начинается с нуля. Во многих научных статьях $\rho$ также называется коэффициентом плотности, потому что его можно также определить следующим образом:

$\rho\left(h\right) = \frac{density\left(h\right)}{density\left(0\right)}$

Разделив истинную плотность на $density\left(0\right)$ , мы получим, что $\rho\left(h\right)$ на уровне моря равно $inline$ . Однако, как подчёркнуто выше, вычисление $density\left(h\right)$ далеко нетривиально. Мы можем аппроксимировать его как экспоненциальную кривую; некоторые из вас уже могли понять, что плотность в нижних слоях атмосферы уменьшается по экспоненте.

Если мы хотим аппроксимировать коэффициент плотности через экспоненциальную кривую, то мы можем сделать это следующим образом:

$\rho\left(h\right) = exp\left\{-\frac{h}{H}\right\}$

где $inline$ — это масштабный коэффициент, называемый приведённой высотой. Для рэлеевского рассеяния в нижних слоях атмосферы Земли часто считается, что $inline$ метрам (см. схему ниже). Для рассеяния света сферической частицей значение часто примерно равно $inline$ метрам.

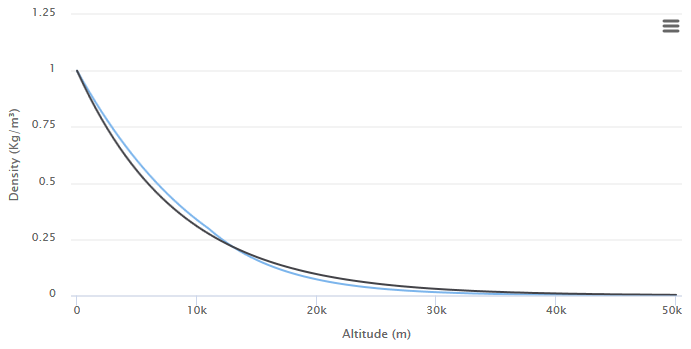
Значение, использованное для $inline$ , не даёт наилучшей аппроксимации $\rho\left(h\right)$ . Однако на самом деле это не проблема. Большинство представленных в этом туториале величин подвергаются серьёзным аппроксимациям. Для создания визуально приятных результатов будет намного эффективнее подгонять имеющиеся параметры под справочные изображения.

Экспоненциальное уменьшение

В предыдущей части туториала мы вывели уравнение, показывающее нам, как учитывать рассеяние наружу, которому подвергается луч света после взаимодействия с отдельной частицей. Величина, использованная для моделирования этого явления, называлась коэффициентом рассеяния $\beta$ . Чтобы учесть его, мы ввели коэффициенты $\beta$ .

В случае рэлеевского рассеяния мы также вывели замкнутую форму для вычисления количества света, подвержденного атмосферному рассеянию при одиночном взаимодействии:

$\beta \left(\lambda, h \right )=\frac{8\pi^3 \left(n^2-1 \right )^2}{3} \frac{\rho\left(h\right)}{N} \frac{1}{\lambda^4}$

При вычислении на уровне моря, то есть при $inline$ , уравнение даёт следующие результаты:

$\beta\left(680nm\right) = 0.00000519673$

$\beta\left(550nm\right) = 0.0000121427$

$\beta\left(440nm\right) = 0.0000296453$

Где $inline$ , $inline$ и $inline$ — длины волн, примерно соответствующие красному, зелёному и синему цветам.

В чём смысл этих чисел? Они представляют собой долю света, которая теряется при одиночном взаимодействии с частицей. Если предположить, что луч света изначально имеет яркость $inline$ и проходит отрезок атмосферы с (общим) коэффицентом рассеяния $\beta$ , то количество сохранившегося после рассеяния света равно:

$I_1=\underset{\text{initial energy}}{\underbrace{I_0}} - \underset{\text{energy lost}}{\underbrace{I_0 \beta}}=I_0 \left(1-\beta\right)$

Это справедливо для единственного столкновения, но нас интересует, какая энергия рассеивается при прохождении определённого расстояния. Это значит, что оставшийся свет подвергается этому процессу в каждой точке.

Когда свет проходит сквозь однородную среду с коэффициентом рассеяния $\beta$ , как мы можем вычислить, какая его часть сохранится при перемещении на определённое расстояние?

Для тех из вас, кто изучал матанализ, это может показаться знакомым. Когда на непрерывном отрезке повторяется мультипликативный процесс $\left(1-\beta\right)$ , то на сцену выходит число Эйлера. Количество света, сохранившегося посте рассеяния после прохождения $inline$ метров равно:

$I = I_0 exp \left\{-\beta x \right\}$

И снова мы столкнулись с экспоненциальной функцией. Она никак не связана с экспоненциальной функцией, описывающей коэффициент плотности $\rho$ . Оба явления описываются экспоненциальными функциями потому, что оба они подвержены экспоненциальному уменьшению. Кроме этого между ними нет никакой связи.

Откуда взялось exp?

Если вы незнакомы с матанализом, то можете не понимать, почему такой простой процесс, как $I_1 = I_0 \left(1-\beta\right)$ преобразуется в $I = I_0 exp \left\{-\beta x \right\}$ .

Мы можем рассматривать исходное выражение как первую аппроксимацию к решению. Если мы хотим получить более близкую аппроксимацию, то нам нужно учитывать два события рассеяния, разделив пополам коэффициент рассеяния для каждого из них:

$I_1 = I_0 \left(1-\frac{\beta}{2}\right)$

$I_2 = \boxed{I_1} \left(1-\frac{\beta}{2}\right)$

Что приводит нас к следующему:

$I_2 = \boxed{I_0 \left(1-\frac{\beta}{2}\right)} \left(1-\frac{\beta}{2}\right)=$

$=I_0 \left(1-\frac{\beta}{2}\right)^2$

Это новое выражение для $inline$ показывает количество сохранившейся после двух столкновений энергии. А как насчёт трёх столкновений? Или четырёх? Или пяти? В общем виде это можно записать следующим выражением:

$I=\lim_{n\rightarrow \infty }I_0 \left(1-\frac{\beta}{n}\right)^n$

где $\lim_{n\rightarrow \infty }$ — это математическая конструкция, позволяющая повторять процесс бесконечное количество раз. Это необходимо нам, потому что $\infty$ технически не является чилом, так как в данном контексте не имеет смысла записывать что-то вроде $\frac{\beta}{\infty}$ .

Это выражение является самим определением экспоненциальной функции:

$\lim_{n\rightarrow \infty } \left(1-\frac{\beta}{n}\right)^n = e^{-\beta}=exp\left\{-\beta\right\}$

которое описывает количество энергии, сохранившееся после мультипликативного процесса на непрерывном интервале.

Равномерное пропускание

Во второй части туториала мы ввели концепцию пропускания $inline$ как доли света, сохраняющейся после процесса рассеяния при прохождении через атмосферу. Теперь у нас есть все элементы, чтобы вывести описывающее его уравнение.

Давайте посмотрим на схему ниже и подумаем, как можно вычислить коэффициент пропускания для отрезка $\overline{CP}$ . Можно легко увидеть, что лучи света, достигающие $inline$ , проходят сквозь пустое пространство. Поэтому они не подвергаются рассеянию. Следовательно, количество света в $inline$ на самом деле равно яркости солнца $inline$ . Во время этого путешествия к $inline$ часть света рассеивается с пути; поэтому количество света, достигающее $inline$ ( $inline$ ), будет меньше, чем $inline$ .

Количество рассеянного света зависит от пройденного расстояния. Чем длиннее путь, тем сильнее будет затухание. Согласно закону экспоненциального уменьшения, количество света в точке $inline$ может быть вычислено следующим образом:

$I_P = I_S \exp{\left\{-\beta \overline{CP}\right\}}$

где $\overline{CP}$ — длина отрезка от $inline$ до $inline$ , а $\exp{\left\{x\right\}}$ — экспоненциальная функция $e^{x}$ .

Атмосферное пропускание

Мы основали наше уравнение на предположении, что вероятность отражения (коэффициент рассеяния $\beta$ одинаков в каждой точке вдоль $\overline{CP}$ . К сожалению, это не так.

Коэффициент рассеяния сильно зависит от плотности атмосферы. Чем больше молекул воздуха на кубический метр, тем выше вероятность столкновения. Плотность атмосферы планеты неоднородна, и изменяется в зависимости от высоты. Это также значит, что мы не можем вычислить рассеяния наружу по $\overline{CP}$ за один этап. Чтобы решить эту проблему, нам нужно вычислить с помощью коэффициента рассеивания рассеивание наружу в каждой точке.

Чтобы понять, как это работает, давайте начнём с аппроксимации. Отрезок $\overline{CP}$ разделён на два, $\overline{CQ}$ и $\overline{QP}$ .

Сначала мы вычисляем количество света от $inline$ , которое достигает $inline$ :

$I_Q = I_S \exp{\left\{-\beta{\left(\lambda, h_0\right)} \overline{CQ} \right\}}$

Затем мы используем тот же подход для вычисления количества света, достигающего $inline$ из $inline$ :

$I_P = \boxed{I_Q} \exp{\left\{-\beta{\left(\lambda, h_1\right)} \overline{QP} \right\}}$

Если мы подставим $inline$ во второе уравнение и упростим, то получим:

Если $\overline{CQ}$ и $\overline{QP}$ имеют одинаковую длину $inline$ , то мы ещё больше можем упростить выражение:

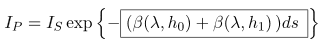
В случае двух отрезков одинаковой длины с разными коэффициентами рассеяния рассеяния наружу вычисляется суммированием коэффициентов рассеяния отдельных отрезков и умноженных на длины отрезков.

Мы можем повторить этот процесс с произвольным количеством отрезков, всё сильнее приближаясь к истинному значению. Это приведёт нас к следующему уравнению:

$I_P = I_S\exp\left\{ -\boxed{ \sum_{Q \in \overline{CP}} { \beta\left( \lambda, h_Q \right) } \, ds } \right \}$

где $inline$ — высота точки $inline$ .

Способ разделения прямой на множество отрезков, который мы только что использовали, называется численным интегрированием.

Если мы предположим, что изначальное количество принятого света равно $inline$ , то получим уравнение атмосферного пропускания через произвольный отрезок:

$T\left(\overline{CP}\right) =\exp\left\{ -\sum_{Q \in \overline{CP}} { \beta\left( \lambda, h_Q \right) } \, ds \right \}$

Мы можем ещё больше развернуть это выражение. заменив общее $\beta$ настоящим значением, использованным в рэлеевском рассеянии, $\beta$ :

$T\left(\overline{CP}\right) =\exp\left\{ -\sum_{Q \in \overline{CP}} { \boxed{\frac{8\pi^3 \left(n^2-1 \right )^2}{3} \frac{\rho\left(h_Q\right)}{N} \frac{1}{\lambda^4}} } \, ds \right \}$

Многие множители $\beta$ постоянны, так что их можно вынести за сумму:

$T\left(\overline{CP}\right) =\exp\left\{ - \underset{\beta\left(\lambda\right)}{ \underset{\text{constant}}{ \underbrace{ \frac{8\pi^3 \left(n^2-1 \right )^2}{3} \frac{1}{N} \frac{1}{\lambda^4} }}} \overset{\text{optical depth}\,D\left(\overline{CP}\right)}{ \overbrace{ \sum_{Q \in \overline{CP}} { \rho\left(h_Q\right) } \, ds}} \right \}$

Выраженная суммированием величина называется оптической толщиной $D\left(\overline{CP}\right)$ , которую мы будем вычислять в шейдере. Оставшаяся часть — это увеличивающий коэффициент, который можно вычислить только один раз, и он соответствует коэффициенту рассеяния на уровне моря. В готовом шейдере мы будем вычислять только оптическую толщину, а коэффициенты рассеяния на уровне моря $\beta$ будем передавать как входные данные.

Подведём итог:

$T\left(\overline{CP}\right) =\exp\left\{ - \beta\left(\lambda\right) D\left(\overline{CP}\right) \right\}$

Часть 5. Атмосферный шейдер.

Введение

Написание шейдера

Мы можем начать писать шейдер для этого эффекта бесконечным количеством способов. Поскольку мы хотим рендерить атмосферное рассеяния на планетах, то логично предположить, что он будет использоваться на сферах.

Если вы используете этот туториал для создания игры, есть вероятность, что вы примените шейдер к уже готовой планете. Добавление вычислений атмосферного рассеяния поверх сверы возможно, но обычно даёт плохие результаты. Причина в том, что атмосфера больше, чем радиус планеты, поэтому её нужно рендерить на прозрачной сфере чуть большего размера. На рисунке ниже показано, как атмосфера простирается над поверхностью планеты, смешиваясь с пустым космосом за ней.

Применение рассеиваемого материала к отдельной сфере возможно, но избыточно. В этом туториале я предлагаю расширить Standard Surface Shader Unity, добавив проход шейдера, который рендерит атмосферу на немного большей сфере. Мы будем называть её атмосферной сферой.

Шейдер с двумя проходами

Если вы раньше работали с поверхностными шейдерами Unity, то могли заметить, что в них нет поддержки блока Pass, с помощью которого в вершинном и фрагментном шейдере задаётся несколько проходов.

Создание шейдера с двумя проходами возможно, достаточно просто добавить два отдельны раздела кода CG в один блок SubShader:

Shader "Custom/NewSurfaceShader" {
 Properties {
 _Color ("Color", Color) = (1,1,1,1)
 _MainTex ("Albedo (RGB)", 2D) = "white" {}
 _Glossiness ("Smoothness", Range(0,1)) = 0.5
 _Metallic ("Metallic", Range(0,1)) = 0.0
 }
 SubShader {
 
 // --- Первый проход ---
 Tags { "RenderType"="Opaque" }
 LOD 200
 
 CGPROGRAM
 // Здесь код Cg
 ENDCG
 // ------------------
 
 // --- Второй проход ---
 Tags { "RenderType"="Opaque" }
 LOD 200
 
 CGPROGRAM
 // Здесь код Cg
 ENDCG
 // -------------------
 }
 FallBack "Diffuse"
}

Можно изменить первый проход для рендеринга планеты. С этого момента мы сосредоточимся на втором проходе, реализовав в нём атмосферное рассеяние.

Экструзия нормалей

Атмосферная сфера чуть больше, чем планета. Это значит, что второй проход должен экструдировать сферу наружу. Если в используемой вами модели применены плавные нормали, то мы можем достичь этого эффекта, воспользовавшись техникой под названием экструзией нормалей.

Экструзия нормалей — один из старейших шейдерных трюков, и обычно его изучают одним из первых. В моём блоге есть множество упоминаний о нём; хорошим началом может стать пост Surface Shader из серии A Gentle Introduction to Shaders.

Если вы незнакомы с тем, как работает экструзия нормалей, то я объясню: все вершины обрабатываются шейдером с помощью его вершинной функции. Мы можем использовать эту функцию для изменения положения каждой вершины, сделав сферу больше.

Первым шагом будет изменение директивы pragma добавлением в неё vertex:vert; это заставит Unity выполнять для каждой вершины функцию vert.

#pragma surface surf StandardScattering vertex:vert
 
void vert (inout appdata_full v, out Input o)
{
 UNITY_INITIALIZE_OUTPUT(Input,o);
 v.vertex.xyz += v.normal * (_AtmosphereRadius - _PlanetRadius);
}

В этом фрагменте кода показана вершинная функция, экструдирующая сферу вдоль её нормалей. Величина экструзии сферы зависит от размера атмосферы и размера планеты. Обе эти величины нужно передавать в шейдер как свойства, к которым можно получить доступ через material inspector.

Нашему шейдеру также нужно знать, где находится центр планеты. Мы можем добавить его расчёт тоже в вершинную функцию. Нахождение центральной точки объекта в пространстве мира мы обсуждали в статье Vertex and Fragment Shaders.

struct Input
{
 float2 uv_MainTex;
 float3 worldPos; // Автоматически инициализируется Unity
 float3 centre;   // Инициализируется в вершинной функции
};
 
void vert (inout appdata_full v, out Input o)
{
 UNITY_INITIALIZE_OUTPUT(Input,o);
 v.vertex.xyz += v.normal * (_AtmosphereRadius - _PlanetRadius);
 o.centre = mul(unity_ObjectToWorld, half4(0,0,0,1));
}

Что такое UNITY_INITIALIZE_OUTPUT?

Если посмотреть на вершинную функцию, то можно заметить, что она всегда содержит таинственный вызов UNITY_INITIALIZE_OUTPUT. Шейдер получает позицию вершин в пространстве объекта, и ему нужно спроецировать их в координаты мира с помощью предоставляемых Unity положения, масштаба и поворота.

И это одна из операций, выполняемых UNITY_INITIALIZE_OUTPUT. Без него нам бы пришлось писать необходимый для этих вычислений код самостоятельно.

Аддитивное смешивание

Ещё одна интересная характеристика, с которой нам нужно разобраться — это прозрачность. Обычно прозрачный материал позволяет видеть, что находится за объектом. Это решение в нашем случае не сработает, потому что атмосфера — это не просто прозрачный кусок пластика. Через неё проходит свет, поэтому нам нужно использовать режим аддитивного смешивания, чтобы увеличить светимость планеты.

В стандартном поверхностном шейдере Unity по умолчанию не включен никакой режим смешивания. Чтобы изменить ситуацию, нам придётся заменить метки во втором проходе на следующие:

Tags { "RenderType"="Transparent"
 "Queue"="Transparent"}
LOD 200
Cull Back
 
Blend One One

Выражение Blend One One используется шейдером для обращения к режиму аддитивного смешивания.

Собственная функция освещения

Чаще всего при написании поверхностного шейдера программисты изменяют его функцию surf, которая используется для обеспечения «физических» свойств, таких как albedo, гладкость поверхности, металлические свойства и т.д. Все эти свойства затем используются шейдером для вычисления реалистичного затенения.

В нашем случае эти вычисления не потребуются. Чтобы избавиться от них, нам нужно удалить используемую шейдером модель освещения. Я подробно рассматривал эту тему; можете изучить следующие посты, чтобы разобраться, как это делать:

3D Printer Shader Effect (перевод на Хабре)
CD-ROM Shader: Diffraction Grating
Fast Subsurface Scattering in Unity (перевод на Хабре)

Новая модель освещения будет называться StandardScattering; мы должны создать функции для освещения в реальном времени и для глобального освещения, то есть, соответственно, LightingStandardScattering и LightingStandardScattering_GI.

В коде, который нам нужно написать, также будут использоваться такие свойства, как направление освещения и направление обзора. Их можно получить с помощью следующего фрагмента кода.

#pragma surface surf StandardScattering vertex:vert
 
#include "UnityPBSLighting.cginc"
inline fixed4 LightingStandardScattering(SurfaceOutputStandard s, fixed3 viewDir, UnityGI gi)
{
 float3 L = gi.light.dir;
 float3 V = viewDir;
 float3 N = s.Normal;
 
 float3 S = L; // Направление освещения от солнца
 float3 D = -V;  // Направление луча видимости, проходящего через атмосферу
 
 ...
}
 
void LightingStandardScattering_GI(SurfaceOutputStandard s, UnityGIInput data, inout UnityGI gi)
{
 LightingStandard_GI(s, data, gi); 
}

В ... будет содержаться сам код шейдера, который нужен для реализации этого эффекта.

Точность чисел с плавающей запятой

В этом туториале мы будем считать, что все вычисления производятся в метрах. Это значит, что если нам нужно симулировать Землю, то потребуется сфера с радиусом 6371000 метров. На самом деле, в Unity это невозможно из-за ошибок чисел с плавающей запятой, которые возникают, когда приходится одновременно работать с очень большими и очень маленькими числами.

Чтобы обойти эти ограничения, можно для компенсации изменить масштаб коэффициента рассеяния. Например, если планета имеет радиус всего 6,371 метров, то коэффициент рассеяния
$\beta\left(\lambda\right)$ должен быть больше в 1000000 раз, а приведённая высота $inline$ — в 1000000 раз меньше.

В моём проекте Unity все свойства и вычисления выражены в метрах. Это позволяет нам использовать реальные, физические значения для коэффициентов рассеяния и приведённой высоты. Однако, шейдер получает в метрах и размер сферы, чтобы он мог выполнить преобразование масштаба из единиц Unity в метры реального масштаба.

Часть 6. Пересечение атмосферы.

Как сказано выше, единственный способ вычисления оптической толщины отрезка, проходящего сквозь атмосферу — это численное интегрирование. Это значит, что нужно разделить интервал на меньшие отрезки длины $inline$ и вычислять оптическую толщину каждого, считая его плотность константой.

На изображении выше оптическая толщина $\overline{AB}$ вычисляется по четырём сэмплам, каждый из кторых учитывает плотность в центре самого отрезка.

Первым шагом, очевидно, будет нахождение точек $inline$ и $inline$ . Если мы предполагаем, что объекты, которые мы рендерим, являются сферой, то Unity попытается отрендерить её повехность. Каждый пиксель на экране соответствует точке на сфере. На рисунке ниже эта точка называется $inline$ (от origin). В поверхностном шейдере $inline$ соответствует переменной worldPos в структуре Input. Вот какой объём работы выполняет шейдер; единственная доступная нам информация — это 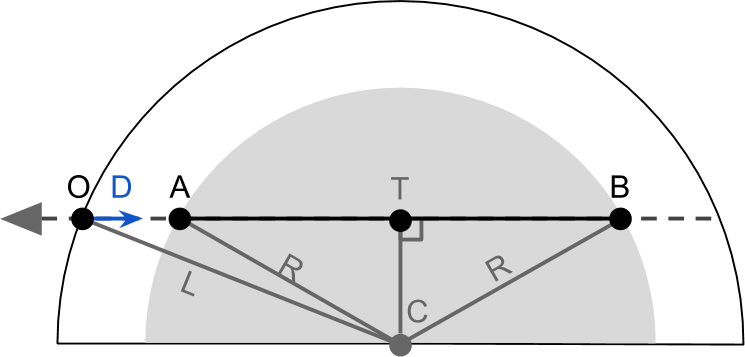$inline$ , направление $inline$ , которое обозначает направление луча видимости, и атмосферная сфера с центром $inline$ и радиусом $inline$ . Сложность заключается в вычислении $inline$ и $inline$ . Быстрее всего будет использовать геометрию, сведя задачу к нахождению пересечения атмосферной сферы и луча видимости камеры.

Во-первых, стоит заметить, что $inline$ , $inline$ и $inline$ лежат на луче видимости. Это значит, что мы можем обращаться с их положением не как с точкой в 3D-пространстве, а как с расстоянием на луча видимости до origin. $inline$ — это реальная точка (представленная в шейдере как float3), а $inline$ — расстояние до точки начала $inline$ (хранящееся как float). $inline$ и $inline$ — два одинаково правильных способа обозначения одной и той же точки, то есть справедливо:

$A = O + \overline{AO}\,D$

$B = O + \overline{BO}\,D$

где запись с чертой сверху $\overline{XY}$ обозначает длину отрезка между двумя произвольными точками $inline$ и $inline$ .

В коде шейдера для эффективности мы будем использовать $inline$ и $inline$ , и вычислять их из $inline$ :

$\overline{AO} = \overline{OT} - \overline{AT}$

$\overline{BO} = \overline{OT} + \overline{BT}$

Также стоит заметить, что отрезки $\overline{AT}$ и $\overline{BT}$ имеют одинаковую длину. Теперь для нахождения точек пересечения нам нужно вычислить $\overline{AO}$ и $\overline{AT}$ .

Отрезок $\overline{OT}$ вычислить проще всего. Если посмотреть на схему выше, то можно увидеть, что $\overline{OT}$ является проекцией вектора $inline$ на луч видимости. Математически это проецирование можно выполнить с помощью скалярного произведения. Если вы знакомы с шейдерами, то можете знать, что скалярное произведение — это мера того, насколько «выровнены» два направления. Когда оно применяется к двум векторам, и один из них имеет единичную длину, то он становится оператором проецирования:

$\overline{OT} = \left(C-O\right) \cdot D$

Стоит также заметить, что
$\left(C-O\right)$ — это трёхмерный вектор, а не длина отрезка между $inline$ и $inline$ .

Далее нам нужно вычислить длину отрезка $\overline{AT}$ . Его можно вычислить с помощью теоремы Пифагона в треугольнике $\overset{\triangle}{ACT}$ . Она утверждает, что:

$R^2 = \overline{AT}^2 + \overline{CT}$

И это значит, что:

$\overline{AT} = \sqrt{R^2 - \overline{CT}}$

Длина $\overline{CT}$ по-прежнему неизвестна. Однако её можно вычислить, снова применив теорему Пифагора к треугольнику $\overset{\triangle}{OCT}$ :

$\overline{CO}^2 = \overline{OT}^2 + \overline{CT}^2$

$\overline{CT} = \sqrt{\overline{CO}^2 - \overline{OT}^2}$

Теперь у нас есть все необходимые величины. Подведём итог:

$\overline{OT} = \left(C-O\right) \cdot D$

$\overline{CT} = \sqrt{\overline{CO}^2 - \overline{OT}^2}$

$\overline{AT} = \sqrt{R^2 - \overline{CT}^2}$

$\overline{AO} = \overline{OT} - \overline{AT}$

$\overline{BO} = \overline{OT} + \overline{AT}$

В этом наборе уравнений есть квадратные корни. Они определены только для неотрицательных чисел. Если $R^2 > \overline{CT}^2$ , то решения не существует, а значит, луч видимости не пересекается со сферой.

Мы можем преобразовать это в следующую функцию Cg:

bool rayIntersect
(
 // Ray
 float3 O, // Origin
 float3 D, // Направление
 
 // Сфера
 float3 C, // Центр
 float R, // Радиус
 out float AO, // Время первого пересечения
 out float BO  // Время второго пересечения
)
{
 float3 L = C - O;
 float DT = dot (L, D);
 float R2 = R * R;
 
 float CT2 = dot(L,L) - DT*DT;
 
 // Точка пересечения за пределами круга
 if (CT2 > R2)
 return false;
 
 float AT = sqrt(R2 - CT2);
 float BT = AT;
 
 AO = DT - AT;
 BO = DT + BT;
 return true;
}

Здесь возвращается не одно, а три значения $\overline{AO}$ , $\overline{BO}$ , а также двоичное значение наличия пересечения. Длины этих двух отрезков возвращаются с помощью ключевых слов out, которые сохраняют после завершения функции любые изменения, которые она внесла в эти параметры.

Столкновение с планетой

Есть ещё одна проблема, которую нужно учитывать. Некоторые лучи видимости сталкиваются с планетой, поэтому их путешествие через атмосферу завершается рано. Один из вариантов решения — пересмотреть выведенное выше.

Более простой, но менее эффективный подход — выполнить rayIntersect дважды и при необходимости изменить конечную точку.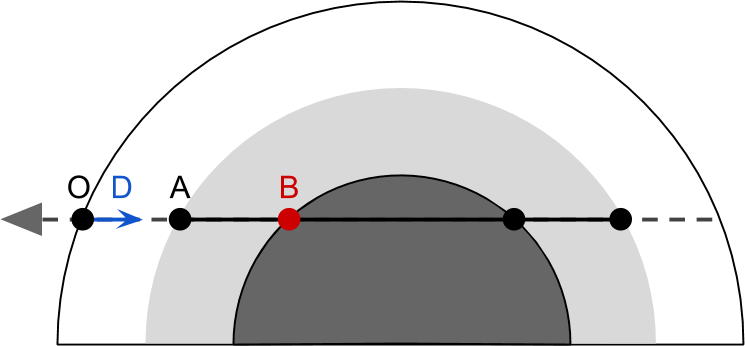

Это преобразуется в следующий код:

// Пересечения с атмосферной сферой
float tA; // Точка входа в атмосферу (worldPos + V * tA)
float tB; // Точка выхода из атмосферы  (worldPos + V * tB)
if (!rayIntersect(O, D, _PlanetCentre, _AtmosphereRadius, tA, tB))
 return fixed4(0,0,0,0); // Лучи видимости смотрят в глубокий космос
 
// Проходит ли луч через ядро планеты?
float pA, pB;
if (rayIntersect(O, D, _PlanetCentre, _PlanetRadius, pA, pB))
 tB = pA;

Часть 7. Шейдер атмосферного рассеяния.

В этой части мы наконец завершим работу над симуляцией рэлеевского рассеяния в атмосфере планеты.

GIF

Сэмплирование луча видимости

Давайте вспомним уравнение атмосферного рассеяния, которое мы недавно вывели:

$I= I_S \sum_{P \in \overline{AB}} {S\left(\lambda, \theta, h\right) T\left(\overline{CP}\right) T\left(\overline{PA}\right) ds }$

Количество получаемого нами света равно количеству света, излучённого солнцем, $inline$ , умноженному на сумму отдельных влияния каждой точки $inline$ на отрезке $\overline{AB}$ .

Мы можем реализовать эту функцию непосредственно в шейдере. Однако здесь нужно внести некоторые оптимизации. В предыдущей части я сказал, что выражение можно упростить ещё больше. Первое, что можно сделать — разбить функцию рассеяния на два основных компонента:

$S \left(\lambda, \theta, h\right ) = \beta \left(\lambda, h \right ) \gamma\left(\theta\right) = \beta \left(\lambda\right )\rho\left(h\right) \gamma\left(\theta\right)$

Фазовая функция $\gamma\left(\theta\right)$ и коэффициент рассеяния на уровне моря $\beta \left(\lambda\right )$ являются константами относительно суммы, потому что угол $\theta$ и длина волны $\lambda$ не зависят от сэмплируемой точки. Поэтому их можно вынести за сумму:

$I = I_S \, \beta \left(\lambda\right ) \gamma\left(\theta\right) \sum_{P \in \overline{AB}} { T\left(\overline{CP}\right) T\left(\overline{PA}\right) \rho\left(h\right) ds }$

Это новое выражение математически аналогично предыдущему, но более эффективно в вычислении, потому что наиболее «тяжёлые» части выведены из суммы.

Мы ещё не готовы к его реализации. Существует бесконечное число точек $inline$ , которые мы должны учесть. Разумной аппроксимацией $inline$ будет разбиение $\overline{AB}$ на несколько более коротких отрезков $inline$ и сложение влияния каждого отдельного отрезка. Сделав так, мы можем предположить, что каждый отрезок достаточно мал, чтобы иметь постоянную плотность. В общем случае это не так, но если $inline$ достаточно мал, то мы можем достичь достаточно хорошей аппроксимации.

Количество отрезков в $\overline{AB}$ мы будем называть сэмплами видимости, потому что все отрезки лежат на луче видимости. В шейдере это будет свойство _ViewSamples. Поскольку это свойство, мы сможем получить к нему доступ из material inspector. Это позволяет нам снизить точность шейдера ради его производительности.

Следующий фрагмент кода позволяет обойти в цикле все отрезки в атмосфере.

// Численное интегрирование для вычисления
// влияния света в каждой точке P отрезка AB
float3 totalViewSamples = 0;
float time = tA;
float ds = (tB-tA) / (float)(_ViewSamples);
for (int i = 0; i < _ViewSamples; i ++)
{
 // Позиция точки
 // (сэмплирование в середине отрезка сэмпла видимости)
 float3 P = O + D * (time + ds * 0.5);
 
 // T(CP) * T(PA) * ρ(h) * ds
 totalViewSamples += viewSampling(P, ds);
 
 time += ds;
}
 
// I = I_S * β(λ) * γ(θ) * totalViewSamples
float3 I = _SunIntensity *  _ScatteringCoefficient * phase * totalViewSamples;

Переменная time используется для отслеживания того, насколько далеко мы находимся от начальной точки $inline$ . После каждой итерации она увеличивается на ds.

Оптическая толщина PA

Каждая точка на луче видимости $\overline{AB}$ вносит свой вклад в конечный цвет отрисовываемого нами пикселя. Этот вклад, выражаясь математически, является величиной внутри суммы:

$I = I_S \, \beta \left(\lambda\right ) \gamma\left(\theta\right) \sum_{P \in \overline{AB}} \underset{\text{light contribution of}\,L\left(P\right)}{\underbrace{T\left(\overline{CP}\right) T\left(\overline{PA}\right) \rho\left(h\right) ds}}$

Давайте попробуем упростить это выражение, как в прошлом параграфе. Мы можем ещё больше развернуть представленное выше выражение, заменив $inline$ его определением:

$T\left(\overline{XY}\right) =\exp\left\{ - \beta\left(\lambda\right) D\left(\overline{XY}\right) \right\}$

Результат пропускания по $\overline{CP}$ и $\overline{PA}$ превращается в:

$T\left(\overline{CP}\right) T\left(\overline{PA}\right)=$

$=\underset{T\left(\overline{CP}\right) }{\underbrace{ \exp\left\{- \beta\left(\lambda\right) D\left(\overline{CP}\right)\right \} }} \, \underset{T\left(\overline{PA}\right) }{\underbrace{ \exp\left\{- \beta\left(\lambda\right) D\left(\overline{PA}\right) \right \} }}=$

$= \exp\left\{- \beta\left(\lambda\right) \left( D\left(\overline{CP}\right) + D\left(\overline{PA}\right) \right) \right \}$

Комбинированное пропускание моделируется как экспоненциальное уменьшение, коэффициентом которого является сумма оптических толщин по пути, пройденному светом ( $\overline{CP}$ и $\overline{PA}$ ), умноженная на коэффициент рассеяния на уровне моря ( $\beta$ при $inline$ ).
Первая величина, которую мы начинаем вычислять, это оптическая толщина отрезка $\overline{PA}$ , который проходит от точки входа в атмосферу до точки, в которой мы в текущий момент сэмплируем в цикле for. Давайте вспомним определение оптической толщины:

$D\left( \overline{PA}\right)=\sum_{Q \in \overline{PA}} { \exp\left\{-\frac{h_Q}{H}\right\} } \, ds$

Если бы пришлось реализовывать его «в лоб», то мы бы создали функцию opticalDepth, сэмплирующую в цикле точки между $inline$ и $inline$ . Это возможно, но очень неэффективно. На самом деле, $D\left( \overline{PA}\right)$ — это оптическая толщина отрезка, который мы уже анализируем в самом внешнем цикле for. Мы можем сэкономить множество вычислений, если вычислим оптическую толщину текущего сегмента, центрированного в $inline$ (opticalDepthSegment), и продолжим суммировать её в цикле for (opticalDepthPA).

// Накопитель оптической толщины
float opticalDepthPA = 0;
 
// Численное интегрирование для вычисления
// влияния света каждой точки P в AB
float time = tA;
float ds = (tB-tA) / (float)(_ViewSamples);
for (int i = 0; i < _ViewSamples; i ++)
{
 // Позиция точки
 // (сэмплируется посередине сэмпла отрезка видимости)
 float3 P = O + D * (time + viewSampleSize*0.5);
 
 // Оптическая толщина текущего отрезка
 // ρ(h) * ds
 float height = distance(C, P) - _PlanetRadius;
 float opticalDepthSegment = exp(-height / _ScaleHeight) * ds;
 
 // Накопление оптических толщин
 // D(PA)
 opticalDepthPA += opticalDepthSegment;
 
 ... 
 
 time += ds;
}

Сэмплирование света

Если мы вернёмся к выражению для влияния света $inline$ , то единственная необходимая величина — это оптическая толщина отрезка $\overline{CP}$ ,

$L\left(P\right) = \underset{\text{combined transmittance}}{\underbrace{\exp\left\{- \beta\left(\lambda\right) \left( D\left(\overline{CP}\right) + D\left(\overline{PA}\right) \right) \right \}}} \, \underset{\text{optical depth of}\,ds}{\underbrace{\rho\left(h\right) ds}}$

Мы переместим код, вычисляющий оптическую толщину отрезка $\overline{CP}$ в функцию под названием lightSampling. Название взято от луча света, который является отрезком, начинающимся в $inline$ и направленным к солнцу. Мы назвали точку, в которой он выходит из атмосферы $inline$ .

Однако функция lightSampling не просто вычисляет оптическую толщину 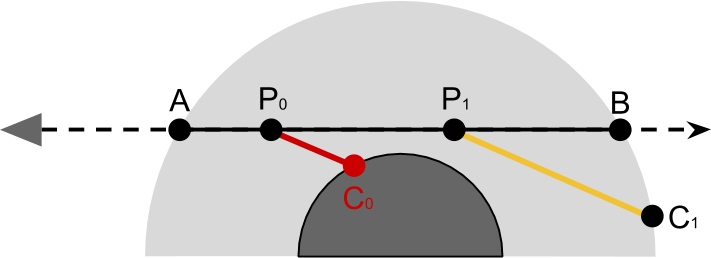$\overline{CP}$ . Пока мы рассматривали только влияние атмосферы и игнорировали роль самой планеты. В наших уравнениях не учитывается возможность того, что луч света, двигающийся из $inline$ к солнцу, может столкнуться с планетой. Если это происходит, то все выполненные до этого момента вычисления неприменимы, потому что свет на самом деле не достигает камеры.

На схеме ниже легко увидеть, что влияние света $inline$ нужно игнорировать, потому что никакой свет солнца не достигает $inline$ . При циклическом перемещении по точкам между $inline$ и $inline$ функция lightSampling также проверяет, не было ли столкновения с планетой. Это можно реализовать проверкой высоты точки на отрицательность.

bool lightSampling
( float3 P, // текущая точка внутри атмосферной сферы
 float3 S, // Направление к солнцу
 out float opticalDepthCA
)
{
 float _; // это нас не интересует
 float C;
 rayInstersect(P, S, _PlanetCentre, _AtmosphereRadius, _, C);
 
 // Сэмплы на отрезке PC
 float time = 0;
 float ds = distance(P, P + S * C) / (float)(_LightSamples);
 for (int i = 0; i < _LightSamples; i ++)
 {
 float3 Q = P + S * (time + lightSampleSize*0.5);
 float height = distance(_PlanetCentre, Q) - _PlanetRadius;
 // Внутри планеты
 if (height < 0)
 return false;
 
 // Оптическая толщина для луча света
 opticalDepthCA += exp(-height / _RayScaleHeight) * ds;
 
 time += ds;
 }
 
 return true;
}

Представленная выше функция сначала вычисляет точку $inline$ с помощью rayInstersect. Затем она разделяет отрезок $\overline{PA}$ на отрезки _LightSamples длиной ds. Вычисление оптической толщины то же самое, которое применяется в самом внешнем цикле.

Функция возвращает false, если произошло столкновение с планетой. Мы можем использовать это для обновления отсутствующего кода самого внешнего цикла, заменив ....

 // D(CP)
 float opticalDepthCP = 0;
 bool overground = lightSampling(P, S);
 
 if (overground)
 {
 // Комбинированное пропускание
 // T(CP) * T(PA) = T(CPA) = exp{ -β(λ) [D(CP) + D(PA)]}
 float transmittance = exp
 (
 -_ScatteringCoefficient *
 (opticalDepthCP + opticalDepthPA)
 );
 
 // Влияния света
 // T(CPA) * ρ(h) * ds
 totalViewSamples += transmittance * opticalDepthSegment;
 }

Теперь, когда мы учли все элементы, наш шейдер готов.

[Прим. пер.: на странице Patreon автора можно купить доступ к Standard и Premium версиям готового шейдера.]

Теги:

Хабы:

Если эта публикация вас вдохновила и вы хотите поддержать автора — не стесняйтесь нажать на кнопку