Георадар (радиотехнический прибор подповерхностного зондирования, GPR, Ground Penetrating Radar), применяющийся в настоящее время весьма широко — от картирования нор кроликов и изучения ящериц до поиска мин, остается достаточно дорогим удовольствием.

Дисплей георадара (кадр из британской телепередачи «Команда времени»)
Но оценить его возможности и изучить различные аспекты взаимодействия электромагнитного поля георадара со средой можно и без приобретения/аренды «железного» устройства. В этом нам поможет пакет gprMax (gpr — от абреввиатуры GPR, Max — начальные буквы фамилии Джеймса Клерка Максвелла, заложившего основы электродинамики), распространяющийся под лицензией GNU GPL v3.
Авторы этого проекта, начатого в 1996 году — Крэйг Уоррен (Craig Warren) из Нортумбрийского университета и Антонис Джианопулос (Antonis Giannopoulos) из Эдинбургского университета. Пакет был изначально разработан на C, а затем полностью переписан на комбинации Python 3/Cython.
Установка пакета требует наличия установленных компилятора, поддерживающего OpenMP (Microsoft Visual C++ 2015 Build Tools (рекомендуется именно эта версия!) для Windows / gcc для Linux), библиотеки NumPy и компилятора Cython. Загрузив из репозитария на GitHub и распаковав исходный код проекта, переходим в корневую папку и выполняем команды:
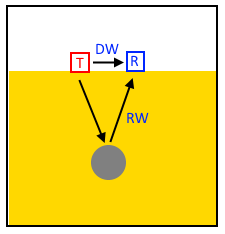
В качестве «быстрого старта» рассмотрим работу с пакетом на несложном двумерном примере — передающая антенна T импульсного радара (impulse GPR) излучает электромагнитный импульс, часть энергии которого непосредственно достигает приемной антенны R в виде прямой волны (DW — direct wave), а часть проникает сквозь песок, отражается от поверхности проводящего цилиндра и достигает приемной антенны в виде отраженной волны (RW — reflected wave):

Формат входного файла
Создадим папку models в корневой папке проекта, в которую поместим текстовый файл hello.in, содержащий команды для выполнения моделирования (приводимые далее команды соответствуют актуальной (третьей) версии проекта).
Каждая команда имеет вид:
На одной строке можно записать только одну команду, причем первым символом строки, содержащей команду, должен быть #.
Команды можно сопровождать комментариями:
Порядок команд важен для команд конструирования объектов — такие команды выполняются в порядке их следования во входном файле.
Форма импульса
Излучаемый георадаром электромагнитный импульс длится единицы-доли наносекунд, причем чаще всего применяются три формы импульса:
Выбираем для нашего примера гауссов импульс (тип импульса — gaussian) с центральной частотой , задаваемый командой:
, задаваемый командой:
(1 — условная амплитуда импульса, pulse — метка импульса)
В этом случае импульс, используемый при моделировании, описывается выражением:
Модель среды и система координат
При 2D-моделировании исследуемая область разбивается на ячейки заданного размера, а система координат модели выглядит так — оси X и Y образуют расчетную плоскость (шириной и высотой
и высотой  ), протяженность модели по оси Z имеет величину, равную шагу дискретизации
), протяженность модели по оси Z имеет величину, равную шагу дискретизации  .
.
При выборе шага дискретизации можно следовать эмпирическому правилу — размер шага не должен превышать одной десятой наименьшей длины волны, исследуемой в модели («10 ячеек на длину волны»):
Для определения длины волны требуется знать максимальную учитываемую частоту в спектре излучаемого сигнала и скорость волны в рассматриваемой среде.
Скорость распространения электромагнитной волны в среде с относительной диэлектрической проницаемостью , выраженная в сантиметрах в наносекунду — принятая в радиолокации единица скорости, определяется выражением:
, выраженная в сантиметрах в наносекунду — принятая в радиолокации единица скорости, определяется выражением:
Длина волны в сантиметрах при этом определяется выражением:
( — частота в ГГц).
— частота в ГГц).
Для вывода формы гауссова импульса и его спектра можно использовать команду:
(gaussian — тип импульса, 1 — амплитуда импульса, 1e9 — центральная частота (1 ГГц), 5e-9 — длительность отображения импульса (5 нс), 1e-12 — шаг по времени (1 пс))

По спектру гауссова импульса с определяем, что на уровне -40 дБ частота
определяем, что на уровне -40 дБ частота  .
.
В рассматриваемом примере средой, в которой находится зондируемый объект, выберем сухой песок с относительной диэлектрической проницаемостью .
.
Найдем скорость распространения электромагнитной волны в песке:
Определим длину волны в песке:
Исходя из этого, выбираем шаг, одинаковый для всех осей ( ) и равный 2 мм = 0,002 м из соображений удобства (в 1 см укладывается целое число шагов):
) и равный 2 мм = 0,002 м из соображений удобства (в 1 см укладывается целое число шагов):
Ограничим моделируемую область прямоугольником шириной , равной 80 см = 0,8 м, и высотой
, равной 80 см = 0,8 м, и высотой  , равной 60 см = 0,6 м:
, равной 60 см = 0,6 м:
(для двумерной модели требуется указать толщину, равную одному шагу (0.002))
Размер области моделирования и величина пространственного шага определяют число ячеек модели и, соответственно, требования к памяти компьютера.
Опишем песок с удельной проводимостью и относительной диэлектрической проницаемостью
и относительной диэлектрической проницаемостью  командой:
командой:
(1 соответствует относительной магнитной проницаемости , равной единице (магнитные свойства отсутствуют), 0 — отсутствию магнитных потерь, а sand — метка этого материала).
, равной единице (магнитные свойства отсутствуют), 0 — отсутствию магнитных потерь, а sand — метка этого материала).
Заполним песком большую часть моделируемой области (от y = 0 до y = 38 см = 0,38 м):
(0 0 0 — координаты левого нижнего угла, 0.80 0.38 0.002 — координаты правого верхнего угла (0.002 — шаг дискретизации))
Оставшаяся часть является свободным пространством (метка free_space), по свойствам практически эквивалентным воздуху ( ,
,  ,
,  ).
).
Границы области моделирования представляются как идеально поглощающий электромагнитное излучение материал (Absorbing Boundary Condition, ABC).
В качестве мишени выберем цилиндр из идеального проводника (полностью отражающий электромагнитное излучение) радиусом 6 см = 0,06 м с центром, расположенным в точке с координатами x = 25 см = 0,25 м и y = 10 см = 0,1 м:
(pec — идеально проводящий материал)
Антенны
Моделируемый георадар оснащен двумя антеннами — передающей и приемной.
В нашем учебном примере представим передающую антенну диполем Герца, длина которого равна шагу дискретизации (в трехмерном случае возможен выбор антенны из обширной библиотеки), лежащим на песке (работа в контакте с зондируемой средой) на расстоянии 5 см слева от середины области (x = 35 см = 0,35 м, y = 38 см = 0,38 м):
(z — ось поляризации диполя (для двумерного случая (2D TMz-режим) допустима только z), pulse — метка формы импульса, излучаемого антенной)
Приемная антенна располагается обычно на небольшом неизменном удалении от приемной, которое называется базой антенного блока (такой вариант взаимного расположения антенн называется «common-offset»). В качестве базы выбираем расстояние 10 см, таким образом, горизонтальная координата равна 35 + 10 = 45 см = 0,45 м (5 см справа от середины области):
Интервал моделирования
Выбор временного окна для моделирования определяется так, чтобы отраженный от мишени сигнал успел достичь приемной антенны.
Определим примерное время, требуемое сигналу в рассматриваемом случае, приняв расстояние от антенн до мишени :
:

Учитывая, что вершина гауссова импульса радара с центральной частотой 1 ГГц сдвинута относительно начала оси времени на 1 нс, выбираем временное окно 5 наносекунд:
Моделирование
Таким образом, содержание входного файл таково:
Запускаем процесс моделирования:
Для выполнения моделирования используется метод конечных разностей во временной области (FDTD, finite-difference time-domain) (базовый алгоритм метода был предложен Кэйном Йи (Kane Yee)), в честь которого ячейки, на которые разбивается модель, названы ячейки Йи (Yee). Численное решение получается во временной области путем решения уравнений Максвелла для каждой ячейки.
В двумерном случае (2D TMz-режим) рассчитываются только компонента электрического поля и компоненты
электрического поля и компоненты  и
и  магнитного поля.
магнитного поля.
При превышении объема доступной памяти выдается сообщение о нехватке памяти для выполнения моделирования:

Если какой-то из объектов вышел за пределы области моделирования, то выдается сообщение об ошибке:

Для выполнения моделирования с описанной моделью потребовалось всего лишь около 56 МБайт оперативной памяти (при уменьшении шага в два раза — до 1 мм — требования к памяти повышаются до 99 МБайт).
После завершения моделирования в папке models появляется файл hello.out, содержащий результаты моделирования в формате HDF5, специально разработанном для хранения численных данных.
Построение трасс
Для визуального представления результатов построим трассы:
Каждая представленная в открывшемся окне трасса (A-scan) отображает временной график одной из составляющих электромагнитного поля в точке расположения приемной антенны:

На трассах видна прямая волна, пришедшая напрямую от передающей антенны (DW), и отраженная от мишени волна (RW).
Горизонтальная ось времени связана с глубиной мишени, отразившей сигнал, через скорость электромагнитной волны в веществе.
А что будет, если поставить во входном файле команду cylinder перед командой box?
Отраженный от цилиндра сигнал исчез — песок поглотил цилиндр (вот такой пример важности порядка следования команд конструирования объектов).
Построение профиля
Но более информативным является радарограмма (radargram) — профиль (B-scan), который является сочетанием множества трасс, построенных при перемещении георадара вдоль заданного направления — это и есть та самая процедура перемещения тележки с радаром по исследуемому участку.
Изменим описание антенн, сместив их к началу горизонтальной оси:
Зададим шаг перемещения антенн, равный 1 см = 0,01 м:
Таким образом, содержание входного файл таково:
Запускаем моделирование в пакетном режиме:
(50 — число шагов перемещения радара).
После запуска последовательно выполняется моделирование для 50 позиций георадара:

После окончания моделирования в папке модели присутствуют 50 файлов hello1.out… hello50.out.
Объединяем эти файлы в файл hello_merged.out командой:
Строим профиль:
(Ez — составляющая электромагнитного поля, по которой строим профиль — компонента, непосредственно преобразуемая в напряжение)

Как видим, на профиле сверху отображается горизонтальная полоса, обусловленная прямой волной, а ниже — характерная гипербола, обусловленная отраженной волной и отображающая изменение расстояния от мишени до георадара при его перемещении.
Легенда справа показывает соответствие цветов и напряженности поля (показанной на трассе):
(показанной на трассе):
красный —
белый —
синий —
Анализируя такие профили, можно делать выводы о глубине, размерах и даже форме мишеней, причем для этого используются и нейронные сети.
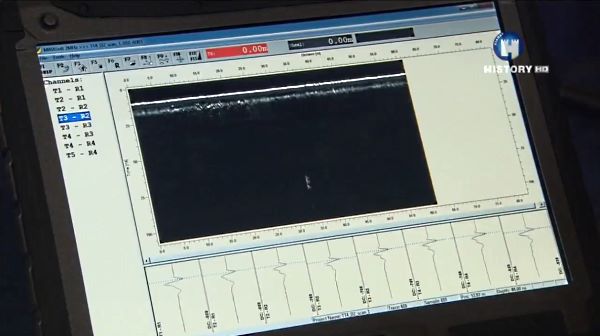
Трассы и профиль на дисплее георадара (кадр из британской телепередачи «Команда времени»)
Но отражение происходит не только от проводящих объектов, но и на границе двух слоев с различной диэлектрической проницаемостью.
Создадим в нижней части модели второй слой песка с диэлектрической проницаемостью :
:
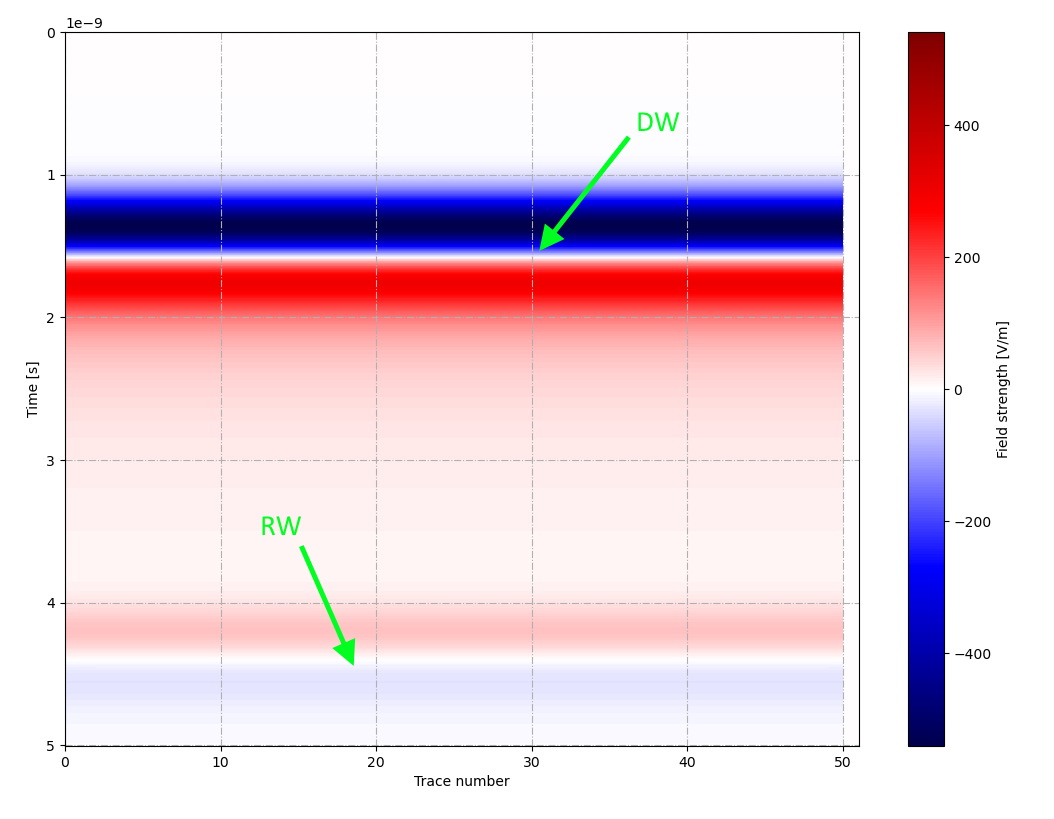
Как видно, ниже «следа» прямой волны (DW) появился линейный сегмент отраженной от границы раздела двух слоев песка волны (RW).
За рамками этого примера остались такие возможности gprMax как трехмерное моделирование, сложные формы поверхности, детальные модели антенн, учет дисперсии электромагнитных волн… При этом пакет можно применять не только для моделирования работы георадара, но и для исследования распространения электромагнитных волн в различных средах, а для ускорения расчетов использовать технологию NVIDIA CUDA, обеспечивающую прирост скорости в десятки раз по сравнению с параллельными вычислениями на CPU посредством OpenMP. Для повышения гибкости моделирования во входном файле можно размещать блоки кода на Python.
Некоторые примеры использования пакета gprMax:
Полезные ссылки:
официальный сайт gprMax
Руководство пользователя gprMax
gprMax на YouTube

Дисплей георадара (кадр из британской телепередачи «Команда времени»)
Но оценить его возможности и изучить различные аспекты взаимодействия электромагнитного поля георадара со средой можно и без приобретения/аренды «железного» устройства. В этом нам поможет пакет gprMax (gpr — от абреввиатуры GPR, Max — начальные буквы фамилии Джеймса Клерка Максвелла, заложившего основы электродинамики), распространяющийся под лицензией GNU GPL v3.
Авторы этого проекта, начатого в 1996 году — Крэйг Уоррен (Craig Warren) из Нортумбрийского университета и Антонис Джианопулос (Antonis Giannopoulos) из Эдинбургского университета. Пакет был изначально разработан на C, а затем полностью переписан на комбинации Python 3/Cython.
Установка пакета требует наличия установленных компилятора, поддерживающего OpenMP (Microsoft Visual C++ 2015 Build Tools (рекомендуется именно эта версия!) для Windows / gcc для Linux), библиотеки NumPy и компилятора Cython. Загрузив из репозитария на GitHub и распаковав исходный код проекта, переходим в корневую папку и выполняем команды:
python setup.py build
python setup.py installВ качестве «быстрого старта» рассмотрим работу с пакетом на несложном двумерном примере — передающая антенна T импульсного радара (impulse GPR) излучает электромагнитный импульс, часть энергии которого непосредственно достигает приемной антенны R в виде прямой волны (DW — direct wave), а часть проникает сквозь песок, отражается от поверхности проводящего цилиндра и достигает приемной антенны в виде отраженной волны (RW — reflected wave):
Формат входного файла
Создадим папку models в корневой папке проекта, в которую поместим текстовый файл hello.in, содержащий команды для выполнения моделирования (приводимые далее команды соответствуют актуальной (третьей) версии проекта).
Каждая команда имеет вид:
#команда: параметр_1 параметр_2 параметр_3 ...На одной строке можно записать только одну команду, причем первым символом строки, содержащей команду, должен быть #.
Команды можно сопровождать комментариями:
##комментарийПорядок команд важен для команд конструирования объектов — такие команды выполняются в порядке их следования во входном файле.
Форма импульса
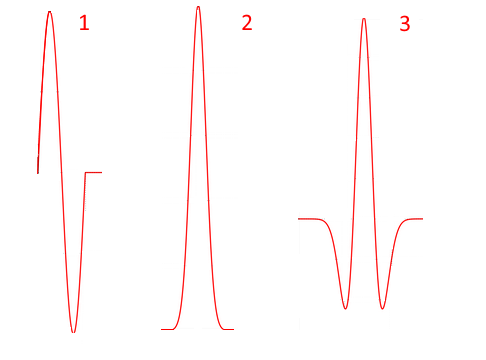
Излучаемый георадаром электромагнитный импульс длится единицы-доли наносекунд, причем чаще всего применяются три формы импульса:
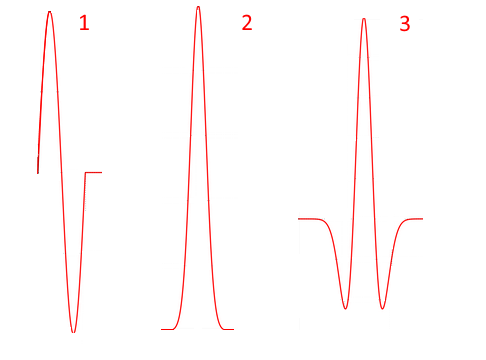
- один период синусоиды (sine)
- гауссов импульс (gaussian)
- «мексиканская шляпа» -«mexican hat» (ricker) — пропорционален второй производной гауссовой функции, форма кривой такого импульса напоминает сомбреро (эта форма импульса была использована американским геофизиком Норманом Рикером (Norman Ricker) в 1953 году при изучении сейсмических сигналов)
Выбираем для нашего примера гауссов импульс (тип импульса — gaussian) с центральной частотой
#waveform: gaussian 1 1e9 pulse(1 — условная амплитуда импульса, pulse — метка импульса)
В этом случае импульс, используемый при моделировании, описывается выражением:
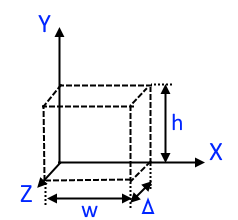
Модель среды и система координат
При 2D-моделировании исследуемая область разбивается на ячейки заданного размера, а система координат модели выглядит так — оси X и Y образуют расчетную плоскость (шириной
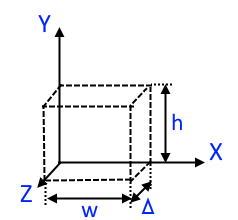
При выборе шага дискретизации можно следовать эмпирическому правилу — размер шага не должен превышать одной десятой наименьшей длины волны, исследуемой в модели («10 ячеек на длину волны»):
Для определения длины волны требуется знать максимальную учитываемую частоту в спектре излучаемого сигнала и скорость волны в рассматриваемой среде.
Скорость распространения электромагнитной волны в среде с относительной диэлектрической проницаемостью
Длина волны в сантиметрах при этом определяется выражением:
(
Для вывода формы гауссова импульса и его спектра можно использовать команду:
python -m tools.plot_source_wave gaussian 1 1e9 5e-9 1e-12 -fft(gaussian — тип импульса, 1 — амплитуда импульса, 1e9 — центральная частота (1 ГГц), 5e-9 — длительность отображения импульса (5 нс), 1e-12 — шаг по времени (1 пс))
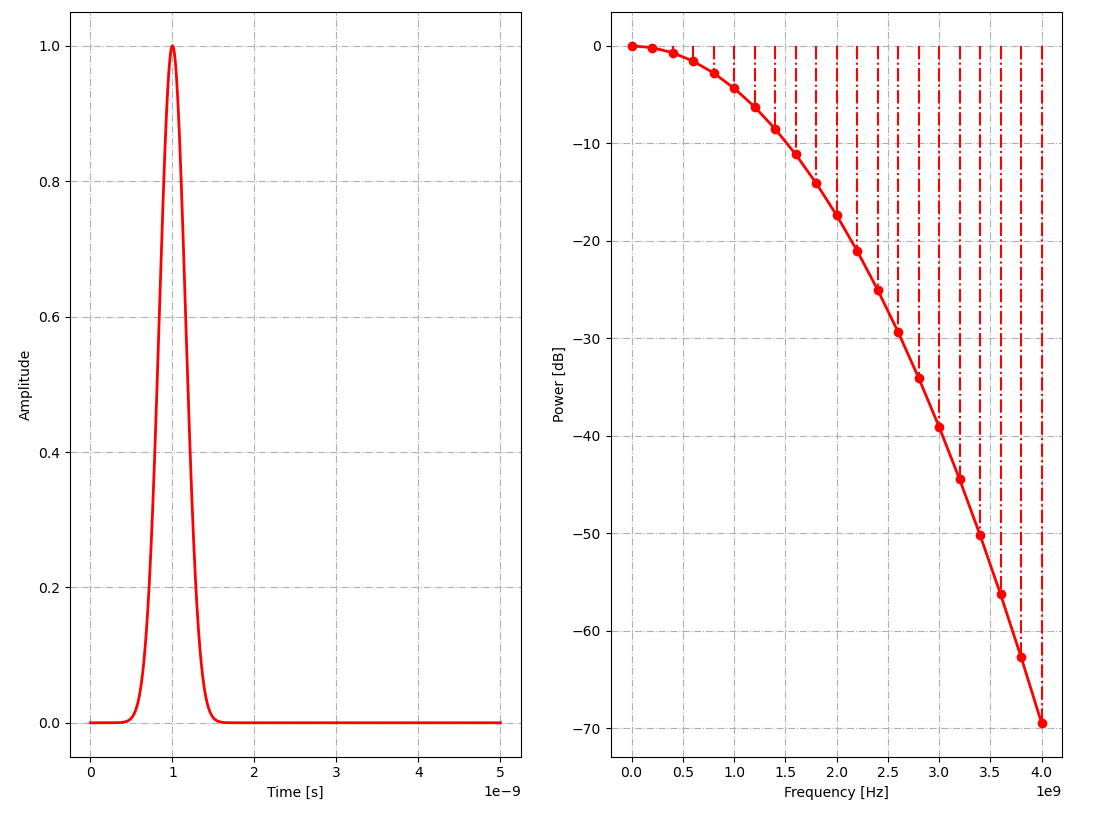
По спектру гауссова импульса с
В рассматриваемом примере средой, в которой находится зондируемый объект, выберем сухой песок с относительной диэлектрической проницаемостью
Найдем скорость распространения электромагнитной волны в песке:
Определим длину волны в песке:
Исходя из этого, выбираем шаг, одинаковый для всех осей (
#dx_dy_dz: 0.002 0.002 0.002Ограничим моделируемую область прямоугольником шириной
#domain: 0.60 0.60 0.002(для двумерной модели требуется указать толщину, равную одному шагу (0.002))
Размер области моделирования и величина пространственного шага определяют число ячеек модели и, соответственно, требования к памяти компьютера.
Опишем песок с удельной проводимостью
#material: 3 0.01 1 0 sand(1 соответствует относительной магнитной проницаемости
Заполним песком большую часть моделируемой области (от y = 0 до y = 38 см = 0,38 м):
#box: 0 0 0 0.80 0.38 0.002 sand(0 0 0 — координаты левого нижнего угла, 0.80 0.38 0.002 — координаты правого верхнего угла (0.002 — шаг дискретизации))
Оставшаяся часть является свободным пространством (метка free_space), по свойствам практически эквивалентным воздуху (
Границы области моделирования представляются как идеально поглощающий электромагнитное излучение материал (Absorbing Boundary Condition, ABC).
В качестве мишени выберем цилиндр из идеального проводника (полностью отражающий электромагнитное излучение) радиусом 6 см = 0,06 м с центром, расположенным в точке с координатами x = 25 см = 0,25 м и y = 10 см = 0,1 м:
#cylinder: 0.250 0.1 0 0.250 0.1 0.002 0.06 pec(pec — идеально проводящий материал)
Антенны
Моделируемый георадар оснащен двумя антеннами — передающей и приемной.
В нашем учебном примере представим передающую антенну диполем Герца, длина которого равна шагу дискретизации (в трехмерном случае возможен выбор антенны из обширной библиотеки), лежащим на песке (работа в контакте с зондируемой средой) на расстоянии 5 см слева от середины области (x = 35 см = 0,35 м, y = 38 см = 0,38 м):
#hertzian_dipole: z 0.35 0.380 0.0 pulse(z — ось поляризации диполя (для двумерного случая (2D TMz-режим) допустима только z), pulse — метка формы импульса, излучаемого антенной)
Приемная антенна располагается обычно на небольшом неизменном удалении от приемной, которое называется базой антенного блока (такой вариант взаимного расположения антенн называется «common-offset»). В качестве базы выбираем расстояние 10 см, таким образом, горизонтальная координата равна 35 + 10 = 45 см = 0,45 м (5 см справа от середины области):
#rx: 0.45 0.38 0.0Интервал моделирования
Выбор временного окна для моделирования определяется так, чтобы отраженный от мишени сигнал успел достичь приемной антенны.
Определим примерное время, требуемое сигналу в рассматриваемом случае, приняв расстояние от антенн до мишени
Учитывая, что вершина гауссова импульса радара с центральной частотой 1 ГГц сдвинута относительно начала оси времени на 1 нс, выбираем временное окно 5 наносекунд:
#time_window: 5e-9Моделирование
Таким образом, содержание входного файл таково:
hello.in
#domain: 0.80 0.60 0.002
#dx_dy_dz: 0.002 0.002 0.002
#time_window: 5e-9
#material: 3 0.01 1 0 sand
#waveform: gaussian 1 1e9 pulse
#hertzian_dipole: z 0.35 0.380 0.0 pulse
#rx: 0.45 0.38 0.0
#box: 0 0 0 0.80 0.38 0.002 sand
#cylinder: 0.40 0.1 0 0.40 0.1 0.002 0.06 pecЗапускаем процесс моделирования:
python -m gprMax models\hello.inДля выполнения моделирования используется метод конечных разностей во временной области (FDTD, finite-difference time-domain) (базовый алгоритм метода был предложен Кэйном Йи (Kane Yee)), в честь которого ячейки, на которые разбивается модель, названы ячейки Йи (Yee). Численное решение получается во временной области путем решения уравнений Максвелла для каждой ячейки.
В двумерном случае (2D TMz-режим) рассчитываются только компонента
При превышении объема доступной памяти выдается сообщение о нехватке памяти для выполнения моделирования:

Если какой-то из объектов вышел за пределы области моделирования, то выдается сообщение об ошибке:

Для выполнения моделирования с описанной моделью потребовалось всего лишь около 56 МБайт оперативной памяти (при уменьшении шага в два раза — до 1 мм — требования к памяти повышаются до 99 МБайт).
После завершения моделирования в папке models появляется файл hello.out, содержащий результаты моделирования в формате HDF5, специально разработанном для хранения численных данных.
Построение трасс
Для визуального представления результатов построим трассы:
python -m tools.plot_Ascan models\hello.outКаждая представленная в открывшемся окне трасса (A-scan) отображает временной график одной из составляющих электромагнитного поля в точке расположения приемной антенны:
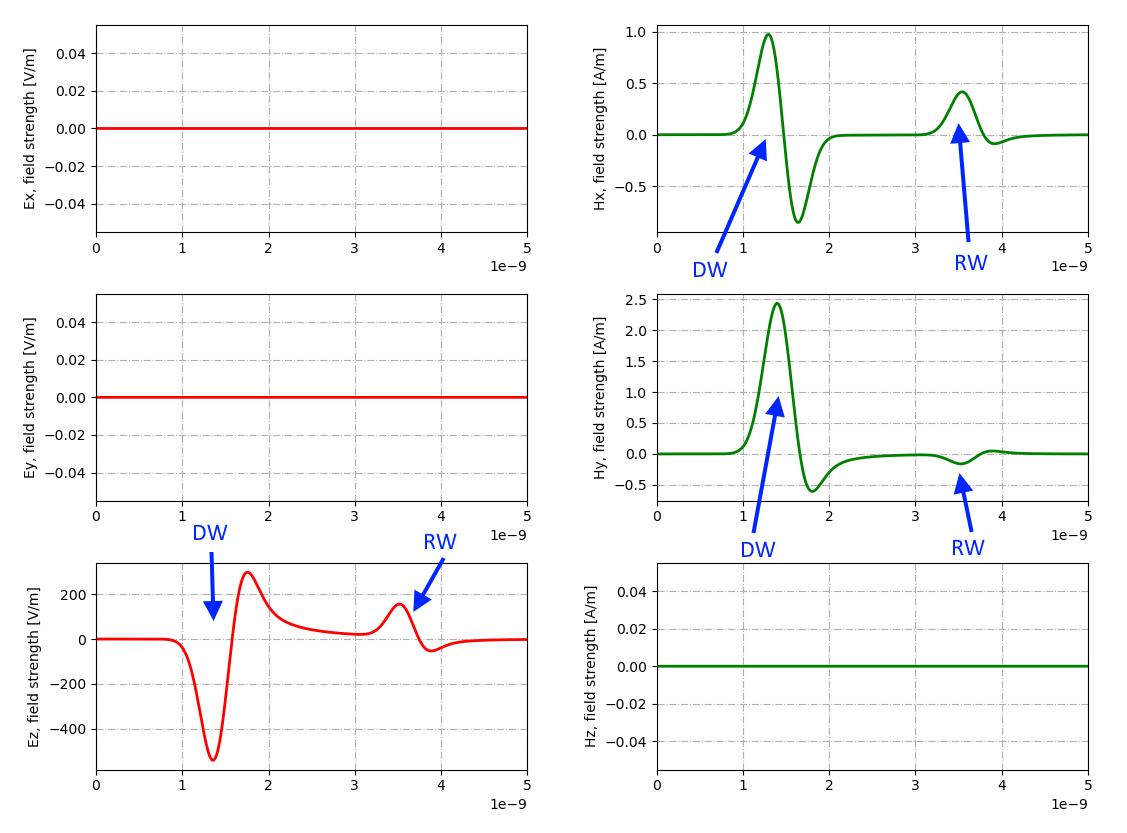
На трассах видна прямая волна, пришедшая напрямую от передающей антенны (DW), и отраженная от мишени волна (RW).
Горизонтальная ось времени связана с глубиной мишени, отразившей сигнал, через скорость электромагнитной волны в веществе.
А что будет, если поставить во входном файле команду cylinder перед командой box?
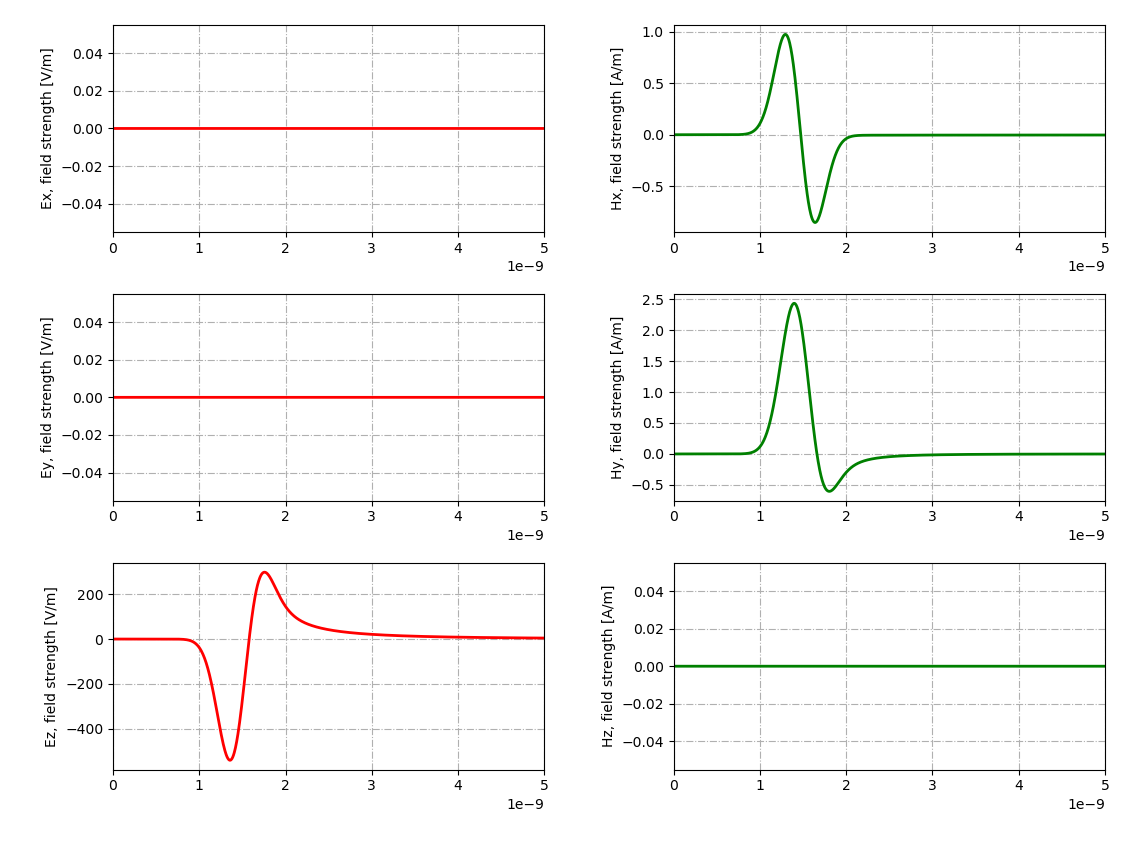
Отраженный от цилиндра сигнал исчез — песок поглотил цилиндр (вот такой пример важности порядка следования команд конструирования объектов).
Построение профиля
Но более информативным является радарограмма (radargram) — профиль (B-scan), который является сочетанием множества трасс, построенных при перемещении георадара вдоль заданного направления — это и есть та самая процедура перемещения тележки с радаром по исследуемому участку.
Изменим описание антенн, сместив их к началу горизонтальной оси:
#hertzian_dipole: z 0.10 0.38 0.0 pulse
#rx: 0.20 0.38 0.0
Зададим шаг перемещения антенн, равный 1 см = 0,01 м:
#src_steps: 0.01 0 0
#rx_steps: 0.01 0 0
Таким образом, содержание входного файл таково:
hello.in
#domain: 0.80 0.60 0.002
#dx_dy_dz: 0.002 0.002 0.002
#time_window: 5e-9
#material: 3 0.01 1 0 sand
#waveform: gaussian 1 1e9 pulse
#hertzian_dipole: z 0.10 0.38 0.0 pulse
#rx: 0.20 0.38 0.0
#src_steps: 0.01 0 0
#rx_steps: 0.01 0 0
#box: 0 0 0 0.80 0.38 0.002 sand
#cylinder: 0.40 0.1 0 0.40 0.1 0.002 0.06 pecЗапускаем моделирование в пакетном режиме:
python -m gprMax models\hello.in -n 50(50 — число шагов перемещения радара).
После запуска последовательно выполняется моделирование для 50 позиций георадара:

После окончания моделирования в папке модели присутствуют 50 файлов hello1.out… hello50.out.
Объединяем эти файлы в файл hello_merged.out командой:
python -m tools.outputfiles_merge models/helloСтроим профиль:
python -m tools.plot_Bscan models\hello_merged.out Ez(Ez — составляющая электромагнитного поля, по которой строим профиль — компонента, непосредственно преобразуемая в напряжение)

Как видим, на профиле сверху отображается горизонтальная полоса, обусловленная прямой волной, а ниже — характерная гипербола, обусловленная отраженной волной и отображающая изменение расстояния от мишени до георадара при его перемещении.
Легенда справа показывает соответствие цветов и напряженности поля
красный —
белый —
синий —
Анализируя такие профили, можно делать выводы о глубине, размерах и даже форме мишеней, причем для этого используются и нейронные сети.
Трассы и профиль на дисплее георадара (кадр из британской телепередачи «Команда времени»)
Но отражение происходит не только от проводящих объектов, но и на границе двух слоев с различной диэлектрической проницаемостью.
Создадим в нижней части модели второй слой песка с диэлектрической проницаемостью
hello.in
#domain: 0.8 0.6 0.002
#dx_dy_dz: 0.002 0.002 0.002
#time_window: 5e-9
#material: 3 0.01 1 0 sand_1
#material: 9 0.01 1 0 sand_2
#waveform: gaussian 1 1e9 pulse
#hertzian_dipole: z 0.10 0.38 0.0 pulse
#rx: 0.20 0.38 0.0
#src_steps: 0.01 0 0
#rx_steps: 0.01 0 0
#box: 0 0 0 0.80 0.38 0.002 sand_1
#box: 0 0 0 0.80 0.10 0.002 sand_2
Как видно, ниже «следа» прямой волны (DW) появился линейный сегмент отраженной от границы раздела двух слоев песка волны (RW).
За рамками этого примера остались такие возможности gprMax как трехмерное моделирование, сложные формы поверхности, детальные модели антенн, учет дисперсии электромагнитных волн… При этом пакет можно применять не только для моделирования работы георадара, но и для исследования распространения электромагнитных волн в различных средах, а для ускорения расчетов использовать технологию NVIDIA CUDA, обеспечивающую прирост скорости в десятки раз по сравнению с параллельными вычислениями на CPU посредством OpenMP. Для повышения гибкости моделирования во входном файле можно размещать блоки кода на Python.
Некоторые примеры использования пакета gprMax:
- оценка влияния свойств грунта на эффективность георадара при поиске противопехотных мин
- проверка возможности использования георадара для недеструктивного определения глубины посадки семян кукурузы
- повышение качества интерпретации полевых данных георадара при исследовании прочности конструкций подземных переходов через магистраль
- исследование связи между амплитудой отраженного сигнала и диаметром арматурных стержней в бетоне
- оценка пригодности георадара для обнаружения пустот в стволах деревьев
Полезные ссылки:
официальный сайт gprMax
Руководство пользователя gprMax
gprMax на YouTube








