d_leonov 19 дек 2020 в 17:37

Ограничения репрезентативной способности и оценка ошибки обобщения для графовых нейронных сетей

5 мин

2.3K

Перевод

Автор оригинала: Vikas K. Garg, Stefanie Jegelka, Tommi Jaakkola

В настоящее время, одним из трендов в исследовании графовых нейронных сетей является анализ работы таких архитектур, сравнение с ядерными методами, оценка сложности и обобщающей способности. Все это помогает понять слабые места существующих моделей и создает пространство для новых.

Работа направлена на исследование двух проблем, связанных с графовыми нейронными сетями. Во-первых, авторы приводят примеры различных по структуре графов, но неразличимых и для простых, и для более мощных GNN. Во-вторых, они ограничивают ошибку обобщения для графовых нейронных сетей точнее, чем VC-границы.

Введение

Графовые нейронные сети - это модели, которые работают напрямую с графами. Они позволяют учитывать информацию о структуре. Типичная GNN включает в себя небольшое число слоев, которые применяются последовательно, обновляя представления вершин на каждой итерации. Примеры популярных архитектур: GCN, GraphSAGE, GAT, GIN.

Процесс обновления эмбеддингов вершин для любой GNN-архитектуры можно обобщить двумя формулами:

$a_v^{t+1} = AGG \left(h_w^t: w \in \mathcal{N}\left(v\right)\right) \\ h_v^{t+1} = COMBINE \left(h_v^t, a_v^{t+1}\right),$

где AGG - обычно функция, инвариантная к перестановкам (sum, mean, max etc.), COMBINE - функция объединяющая представление вершины и ее соседей.

Дерево вычислений для двухслойной GNN на примере узла A. Источник: https://eng.uber.com/uber-eats-graph-learning/

Более продвинутые архитектуры могут учитывать дополнительную информацию, например, фичи ребер, углы между ребрами и т.д.

В статье рассматривается класс GNN для задачи graph classification. Эти модели устроены так:

Сначала производятся эмбеддинги вершин с помощью L шагов графовых сверток
Из эмбеддингов вершин получают представление графа с помощью инвариантной к перестановкам функций (например, sum, mean, max)
Классификатор предсказывает бинарную метку по представлению графа

Ограничения графовых нейронных сетей

В статье авторы рассматривают ограничения для трех классов GNN:

Локально инвариантные графовые нейронные сети (LU-GNN). Сюда входят вышеупомянутые GCN, GraphSAGE, GAT, GIN и другие
CPNGNN, которая вводит локальный порядок, нумеруя соседние вершины от 1 до d, где d - степень вершины (в оригинальной работе это называют port numbering)
DimeNet, которая оперирует 3D-графами, учитывая расстояния между вершинами и углы между ребрами

Ограничения LU-GNN

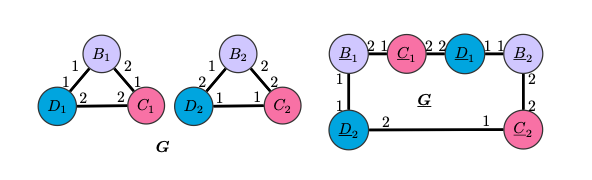
Графы G и G неразличимы LU-GNN, так как деревья вычислений будут совпадать для узлов одного цвета, следовательно эмбеддинги, полученные с помощью инвариантной к перестановкам readout-функции, будут одинаковыми. CPNGNN с введением подходящего порядка сможет различать как одноцветные вершины в G и G, так и сами графы.

Ограничения CPNGNN

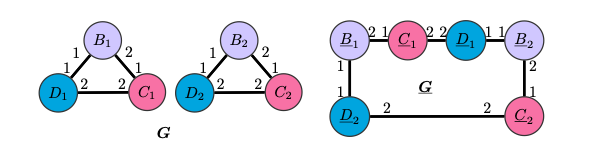
Однако, существует “плохой” порядок, при котором и CPNGNN произведет одинаковые эмбеддинги для вершин одного цвета.

Граф S₈ и две копии S₄ различаются в таких характеристиках, как обхват, окружность (длина наименьшего и наибольшего циклов соответственно), радиус, диаметр и количество циклов, но CPNGNN с таким порядком портов и readout-ом, инвариантным к перестановкам, произведет для одинаковые эмбеддинги. А значит, по ним невозможно будет восстановить правильные характеристики для обоих графов.

Здесь CPNGNN с такими же условиями не сможет восстановить характеристики из предыдущего примера для графа G₂и двух копий G₁. Однако, DimeNet сможет это сделать, так как она учитывает углы, которые не везде совпадают в случае этих графов, например, $\angle A_1B_1C_1$ и $\angle \underline{A}_1\underline{B}_1\underline{C}_1$ .

Ограничения DimeNet

DimeNet не сможет различить G₄ и граф, составленный из двух копий G₃, так как расстояния и углы в этих графах будут идентичны. Значит, она так же не вычислит характеристики обоих графов. Можно заметить, что G₄ и G₃ являются графами S₄ и S₈, натянутыми на куб, а значит, даже усовершенствованная версия DimeNet с нумерацией портов из S₄ и S₈ не будет справляться с этой задачей.

Шаг в сторону более мощных GNN

Авторы предлагают объединить идеи вышеупомянутых подходов и добавить больше геометрической информации. Например, включить углы и расстояния между плоскостями, которые будут заданы тройкой ребер.

GNN, предложенная авторами работает так:

Шаг DimeNet
Дополнение message-эмбеддинга ребра $m_{uv}^{\left(l\right)}$ геометрической информацией $\Phi_{uv}$ по формуле $\underline{m}_{uv}^{\left(l\right)} = \underline{f}\left(m_{uv}^{\left(l\right)}, \Phi_{uv}\right)$
Получение эмбеддинга вершины с учетом введенного локального порядка $\left(c_v\left(i\right), t_{i, v}\right)$ , где c - i-ый сосед вершины v, t - эмбеддинг порядка.

Формула обновления представления вершины:

$h_{v}^{\left( l + 1 \right)} = f \left( h_{v}^{\left( l \right)}, \underline{m}_{c_v\left( 1 \right)v}^{\left( l \right )}, t_{1, v}, ..., \underline{m}_{c_v\left( d \left( v \right ) \right)v}^{\left( l \right )}, t_{ d \left( v \right ), v} \right )$
Шаг инвариантного к перестановкам readout-а
Классификатор или регрессор в зависимости от задачи

Такая модель позволит различать графы во всех вышеприведенных примерах.

Оценка ошибки обобщения

Авторы рассматривают конкретный класс моделей: LU-GNN, в которой обновление представления вершины происходит согласно

$h_v^{l + 1} = \phi \left( W_1x_v + W_2 \rho \left( \sum_{u \in \mathcal{N} \left( v \right)} g\left( h_u^l \right)\right) \right),$

где $\phi,\ g,\ \rho$ - нелинейные функции активации, x_v - вектор признаков для вершины v, такие, что $\rho \left(0\right) = 0,\ \forall v: \lVert x_v \rVert_2 \le B_x,\ \forall x \in \mathbb{R}^r: \lVert \phi \left( x \right ) \rVert_{\infty} \le b < \infty,\ \phi\left( 0 \right ) = 0,\ g\left( 0 \right ) = 0$ . Также, $\phi,\ g,\ \rho$ липшицевы с константами $C_{\phi},\ C_{g},\ C_{\rho}$ соответственно, а $\lVert W_1 \rVert_2 \le B_1,\ \lVert W_2 \rVert_2 \le B_2$ . $W_1,\ W_2,\ \phi,\ g,\ \rho$ одинаковы на всех слоях GNN.
Далее бинарный классификатор применяется к представлению каждой вершины отдельно и полученные метки усредняются. Параметр $\beta$ бинарного классификатора обладает свойством $\lVert \beta \rVert_2 \le B_{\beta}$ .

Пусть $f\left(G\right)$ - результат применения GNN к графу с меткой $y \in \{0, 1\}$ , $p\left( f \left( G \right ), y \right ) = y \left( 2f \left( G \right ) - 1 \right ) + \left( 1 - y \right ) \left( 1 - 2 f \left( G \right ) \right )$ - разница между вероятностями правильного и неправильного лейбла, $p\left( f \left( G \right ), y \right ) < 0$ только в случае ошибки классификации.

Фукнция потерь, где $a = -p\left( f \left( G \right ), y \right )$ , $\mathbb{I}\left[\right]$ - индикаторная функция:

$loss_{\gamma}\left( a \right ) = \mathbb{I}\left[ a > 0\right ] + (1 + \frac{a}{\gamma})\mathbb{I}\left[ a \in \left[ \gamma, 0 \right ] \right].$

Тогда эмпирическая сложность Радемахера для класса функций предсказания GNN на тренировочном множестве $\{G_j, y_j\}_{j=1}^m$ :

$\hat{\mathcal{R}}\left( f \right) = \frac{1}{m} \sum_{j = 1}^m loss_{\gamma} \left( -p\left( f \left(G_j\right), y_j \right) \right)$

Авторы строят доказательство, пользуясь леммой, в которой утверждается, что с большой вероятностью, ошибку предсказания для GNN можно ограничить суммой ошибки на тренировочной выборке и способностью модели предсказывать класс по эмбеддингу графа. Для класса, рассматриваемого авторами (GNN, которые предсказывают метку графа по меткам большинства вершин), второе слагаемое можно заменить на способность предсказывать класс по вершинам, то есть деревьям вычислений, следовательно можно анализировать эти деревья.

Все вышеописанное было проделано для того, чтобы можно было использовать два факта:

Так как исследуется дерево, можно выразить эмбеддинг вершины рекурсивно через поддеревья
Малые изменения в весах модели так же вносят малый вклад в изменение класса (доказательство приведено в статье)

Это позволяет вывести границы ошибки обобщения по аналогии с RNN

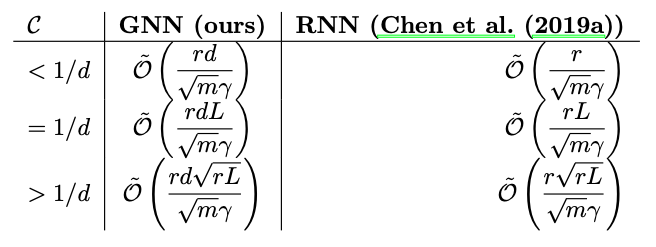
В таблице $\mathcal{C}$ - “сложность перколяции”: $\mathcal{C} = C_{\phi}C_gC_{\rho}B_2$ , r - размер эмбеддинга, d - максимальная степень вершины, m - размер тренировочной выборки, L - количество слоев, $\gamma$ - зазор, зависящий от данных

Эти оценки позволяют существенно более точно оценить ошибку обобщения, по сравнению с работой, где получили оценку $\tilde{\mathcal{O}} \left(r^3N / \sqrt{m} \right)$

Важной частью этой статьи является использование локальной инвариантности к перестановкам внутри GNN, а не только глобальной (в readout-е), как в этой и этой статьях. Это позволяет более точно оценить ошибку обобщения, так как не приходится учитывать каждый порядок, в котором могут быть расположены вершины графа.

Выводы

Важна как мощность модели (способность различать всевозможные пары графов), так и ее обобщающая способность. Однако, более сложные модели склонны к переобучению, поэтому нужно выбирать модели, которые находят баланс, например, исходя из размера датасета, вычислительных ресурсов и других факторов.

С доказательствами и более подробной информацией можно ознакомиться, прочитав оригинальную статью или посмотрев доклад от одного из авторов.

Теги:

Хабы:

Ограничения репрезентативной способности и оценка ошибки обобщения для графовых нейронных сетей

Введение

Ограничения графовых нейронных сетей

Ограничения LU-GNN

Ограничения CPNGNN

Ограничения DimeNet

Шаг в сторону более мощных GNN

Оценка ошибки обобщения

Выводы

Публикации

Истории

Работа

Ближайшие события