Введение
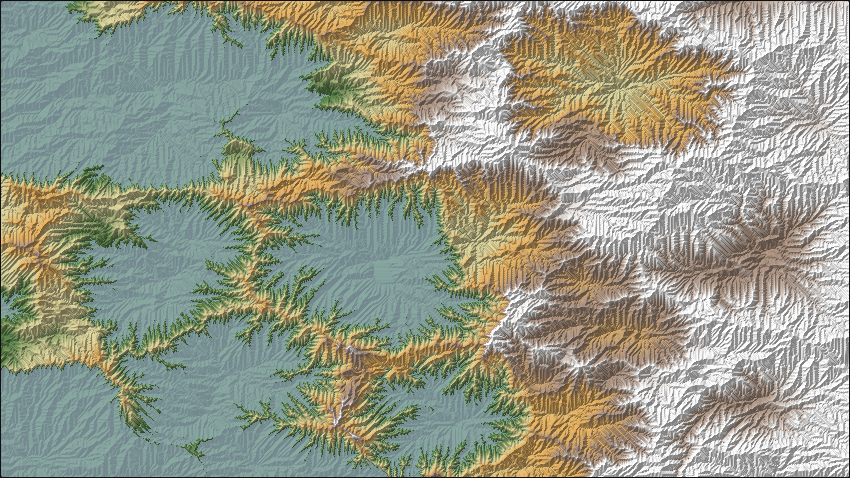
В этом посте я расскажу о реализации моей процедурной симуляции Земли, написанной целиком на фрагментных шейдерах GLSL. Она за несколько минут симулирует полную историю землеподобной планеты с частотой 60 кадров в секунду.
Протопланета
Эта история начинается четыре с половиной миллиарда лет назад с куска расплавленного камня...

Шейдер: https://www.shadertoy.com/view/XsGBDt
Молодая Земля была протопланетой, раскалённой докрасна и испещрённой кратерами от столкновений с астероидами. Так как моя симуляция Земли полностью генерируется процедурно, без заранее отрендеренных текстур, первым делом нужно было сгенерировать карту этого рельефа. Для вычисления высоты
height рельефа в заданной широте lat и долготе lon, необходимо сначала выполнить преобразование в декартовы 3D-координаты:vec3 p = 1.5 * vec3(
sin(lon*PI/180.) * cos(lat*PI/180.),
sin(lat*PI/180.),
cos(lon*PI/180.) * cos(lat*PI/180.));Так как астероиды имеют разные размеры, остающиеся от них кратеры тоже должны быть разными. Чтобы реализовать это, шейдер выполняет итерации по пяти уровням детализации, накладывая друг на друга кратеры уменьшающегося размера. Чтобы кратеры выглядели реалистично, изображение смешивается с шумом дробного броуновского движения и масштабируется таким образом, чтобы самые крупные кратеры сильнее всего влияли на рельеф.
float height = 0.;
for (float i = 0.; i < 5.; i++) {
float c = craters(0.4 * pow(2.2, i) * p);
float noise = 0.4 * exp(-3. * c) * FBM(10. * p);
float w = clamp(3. * pow(0.4, i), 0., 1.);
height += w * (c + noise);
}
height = pow(height, 3.);Сами кратеры генерируются на 3D-сетке, из которой вырезается сетка для рельефа поверхности. Чтобы избежать повторяемости паттерна, центрам кратеров придаются псевдослучайные смещения от точек сетки при помощи хэш-функции. Для вычисления влияния кратера в конкретной точке мы берём взвешенное среднее кратеров, принадлежащих ближайших точек сетки; веса при этом экспоненциально уменьшаются с расстоянием от центра. Борта кратеров генерируются простой синусоидой.
float craters(vec3 x) {
vec3 p = floor(x);
vec3 f = fract(x);
float va = 0.;
float wt = 0.;
for (int i = -2; i <= 2; i++)
for (int j = -2; j <= 2; j++)
for (int k = -2; k <= 2; k++) {
vec3 g = vec3(i,j,k);
vec3 o = 0.8 * hash33(p + g);
float d = distance(f - g, o);
float w = exp(-4. * d);
va += w * sin(2.*PI * sqrt(d));
wt += w;
}
return abs(va / wt);
}Готовая процедурно сгенерированная карта высот выглядит так:
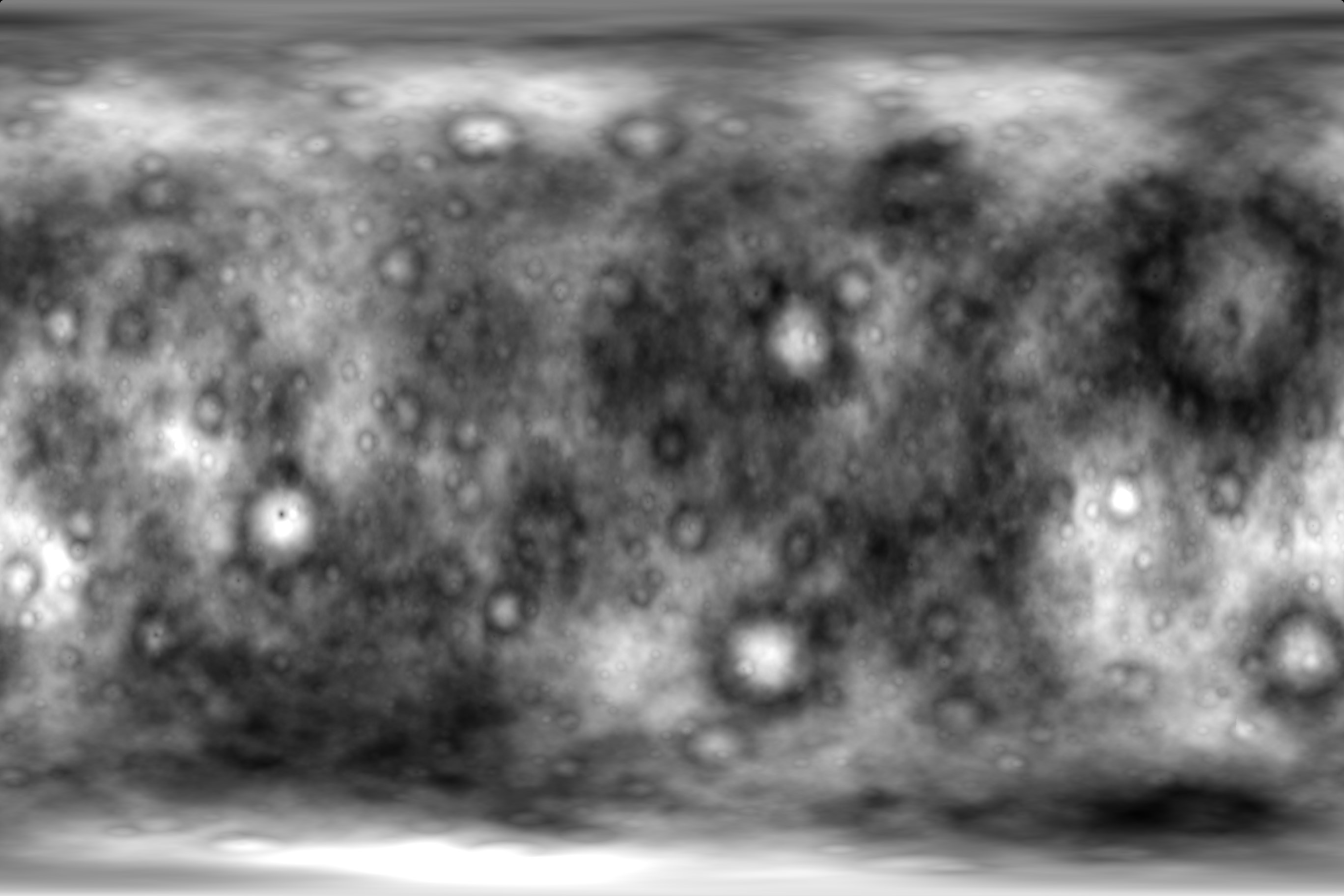
Хотя система довольно проста, после заполнения низко расположенных областей водой процедурный рельеф напоминает то, как, по мнению учёных выглядела молодая Земля:

Художественное изображение молодой Земли, созданное НАСА.
Содержавшаяся внутри вода испарялась под воздействием тепла, затем улетучивалась и начинала циркулировать в первой атмосфере, формировавшейся вокруг планеты. С течением времени камень охлаждался и водяной пар конденсировался в океаны. Поток жидкой воды по поверхности вымывал в рельефе долины, оставляя накопившиеся осадочные породы по течению.
Тектонические плиты
Для образования гор, океанических впадин и привычных нам континентальных очертаний суши требуется модель тектонических сдвигов. Симуляция случайным образом генерирует порождающие точки для плит с начальной скоростью. Эти плиты постепенно растут в размерах благодаря простой модели агрегирования, которая случайным образом выбирает соседние точки и добавляет их к плите, если они ещё не принадлежат другой плите. Все пиксели в пределах плиты хранят скорость движения плиты. Модель агрегирования похожа на модель ограниченного диффузией агрегирования (но без диффузии):

Шейдер: https://www.shadertoy.com/view/ldK3RW
Непрерывное движение плит реализовать сложно, поскольку для этого потребуется, чтобы границы плит учитывали движение, измеряемое в долях пикселя. Чтобы избежать этого, система двигает плиты с дискретными шагами времени на целый пиксель по вертикали или горизонтали. Эти промежутки времени для каждой плиты рандомизированы таким образом, чтобы средняя скорость соответствовала заданной скорости и направлению, а также чтобы снизить вероятность одновременного движения соседних плит.
Столкновения плит происходят, когда часть пикселей границы одной плиты перемещаются в место, ранее занятое пикселями другой плиты. Это приводит к созданию зоны субдукции, которая моделируется простым увеличением высоты рельефа в местах столкновения. Хотя это происходит только в пикселях вдоль границы плиты, влияние постепенно распространяется на соседние пиксели при помощи простой модели термической эрозии, которая подталкивает высоту пикселя в направлении среднего от её соседей.
В целом это создаёт правдивую симуляцию образования континентов с горными грядами (которые будут совершенствоваться благодаря добавлению гидравлической эрозии):

Шейдер: https://www.shadertoy.com/view/XtffW8
Гидравлическая эрозия
Изломанность природного рельефа в основном вызвана образованием бассейнов рек, эрозией преобразующих ландшафты в знакомый нам паттерн ветвления. Для выполнения этой задачи существует множество разных симуляций течения воды, однако сложность здесь заключается в том, что разрешение карты рельефа довольно низко для целой планеты. Следовательно, модель должна уметь симулировать реки шириной не больше одного пикселя. Барнс (2018 год) предложил простую модель, решающую именно эту задачу.
Если вкратце, каждый пиксель сравнивает восемь своих соседей, чтобы определить, какой из направлений имеет наибольшее снижение высоты (с учётом того, что соседи по диагонали расположены дальше). В направлении с наибольшим наклоном переместится вода, вытекающая из этого пикселя. Изначально вода распределяется по ячейкам осадками, которые затем передаются между соседними пикселями на каждом шаге времени.
Эрозией управляет степенной закон потока:
elevation -= 0.05 * pow(water, 0.8) * pow(slope, 2.);Здесь у нас есть высота
elevation и количество воды water, расположенной в текущей ячейке, а также наклон slope в направлении, в котором перемещается вода. Снижение высоты ограничено, чтобы оно не становилось ниже, чем точка, в которую течёт вода.Взаимодействие между потоком воды и эрозии приводит к естественному образованию бассейнов рек на рельефе:

Шейдер: https://www.shadertoy.com/view/XsVBRm
Раскрасив связанные друг с другом водные пути (цветом, определяемым расположением устья реки), мы можем создавать потрясающие визуализации. напоминающие карты бассейнов реальных рек:

Симулируемые бассейны рек. Исходный шейдер.

Бассейны рек США, Grasshopper Geography.
Глобальный климат
Симуляция климатической системы целой планеты — пугающая задача, но, к счастью, её довольно просто можно аппроксимировать. Движущей силой, управляющей всем в моей симуляции климата, будет процедурно генерируемая карта среднего давления на уровне моря (mean sea-level pressure, MSLP).
Согласно «Поваренной книге климата», основными ингредиентами создания карты MSLP являются очертания суши посреди океана и влияние широты. На самом деле, если взять данные из реальной карты MSLP Земли, отделить точки в соответствии с тем, являются ли они сушей или океаном, и наложить MSLP в соответствии с широтой, то мы получим две синусоиды (для суши и океана) со слегка отличающимися формами.
Настроив параметры, я получил очень грубую модель ежегодного среднего давления (здесь широта
lat измеряется в градусах):if (land) {
mslp = 1012.5 - 6. * cos(lat*PI/45.);
} else { // ocean
mslp = 1014.5 - 20. * cos(lat*PI/30.);
}Разумеется, этого не совсем достаточно для генерации реалистичной карты MSLP, так как генерация значений по отдельности для суши и океана приводит к резким разрывам на границах между ними. В реальности MSLP плавно меняется на переходе между океаном и сушей из-за локальной диффузии давления газов. Этот процесс диффузии можно аппроксимировать простым применением к карте MSLP гауссова размытия (со стандартным отклонением 10-15 градусов).
Чтобы климат менялся вместе с временами года, необходимо также смоделировать разницу в MSLP между январём и июлем. Полученные на Земле данные опять-таки дают понять, что она следует паттерну синусоид. Подогнав параметры и применив гауссово размытие, мы можем скомбинировать его с картой ежегодного MSLP, чтобы сгенерировать динамические паттерны климата, меняющегося на протяжении года.
if (land) {
delta = 15. * sin(lat*PI/90.);
} else { // ocean
delta = 20. * sin(lat*PI/35.) * abs(lat)/90.;
}Имея MSLP, можно сгенерировать ветровые потоки и температуры. На самом деле, в реальности температура генерирует давление, но корреляция есть корреляция. Для генерации реалистичных значений необходимо чуть больше экспериментов (на протяжении года
season колеблется от -1 до 1):float temp = 40. * tanh(2.2 * exp(-0.5 * pow((lat + 5. * season)/30., 2.)))
- 15. - (mslp - 1012.) / 1.8 + 1.5 * land - 4. * elevation;Ветер обычно движется от высокого давления к низкому, но в глобальном масштабе нам нужно учесть и силу Кориолиса, отвечающую за циркуляцию ветров вокруг зон давления (
grad — это вектор градиента MSLP):vec2 coriolis = 15. * sin(lat*PI/180.) * vec2(-grad.y, grad.x);
vec2 velocity = coriolis - grad;Несмотря на довольно грубую симуляцию, модель создаёт очень реалистчные паттерны циркуляции ветров. Если присмотреться, можно заметить, что воссоздаётся множество природных явлений, в том числе и скачки ветров над Индией во время сезона муссонов:

Шейдер: https://www.shadertoy.com/view/MdGBWG
В качестве последней детали можно симулировать осадки адвекцией водяного пара с океана через векторное поле ветров на сушу:

Шейдер: https://www.shadertoy.com/view/MdKfWK
Адвекция реализуется похоже на симуляцию жидкостей:

Шейдер: https://www.shadertoy.com/view/XlsBDf
Жизнь
Климат влияет на распределение жизни по планете. Паттерны выпадения осадков и колебаний температуры диктуют скорость роста растений. При смене времён года травоядные мигрируют в регионы, где достаточно растительности для их жизни. И поскольку они следуют за растительностью, хищники следуют за ними. Всю эту динамику можно передать моделью диффузии Лотки-Вольтерры:
float dx = plant_growth - c.y;
float dy = reproduction * c.x - predation * c.z - 1.;
float dz = predation * c.y - 1.;
float dt = 0.1;
c.xyz += dt * c.xyz * vec3(dx, dy, dz);Элементы
xyz переменной c представляют собой популяции растительности, травоядных и хищников. В крупном масштабе динамика популяций животных генерирует интересные паттерны:
Шейдер: https://www.shadertoy.com/view/Xtcyzr
В реальной жизни подобные паттерны проще всего увидеть в популяциях микробов в чашке Петри, но те же самые законы управляют популяциями крупных животных по всему миру
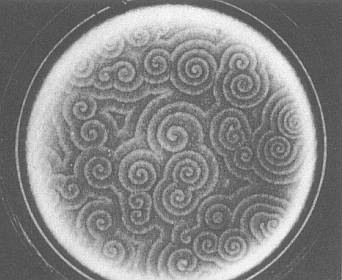
Спиральные волны колоний в плесени.
Человечество
Завершая прелюдию молодой Земли, замедлился цикл смены дня и ночи. Рельеф обрёл постоянство, потому что тектонические сдвиги стали незаметными. Вскоре ночь выявила невиданные ранее паттерны света в процессе расселения человечества по поверхности планеты.
Это быстрое разрастание принесло с собой свои изменения — люди начали сжигать огромные объёмы ископаемого топлива для обогрева и освещения своих поселений. Углерод, дремавший миллионы лет, оказался выброшенным в атмосферу и распространился по планете.
За несколько сотен лет люди сожгли все доступные ресурсы ископаемого топлива, выбросив в атмосферу пять триллионов тонн углерода. Это усилило парниковый эффект, подняв среднюю температуру в мире почти на 10 градусов Цельсия. Большие регионы суши рядом с экватором признаны непригодными для жизни из-за экстремальных температур, что привело к исчезновению человечества со значительной части планеты.












