Yermack 5 окт 2021 в 11:01

Кадрим девчонок с помощью метрики Эллиса-Бронникова

11 мин

29K

Туториал

В прошлой статье мы как следует повосторгались полевым уравнением Эйнштейна, повыводили уравнения движения для планет и посмотрели такое количество ~~умных видевов и книгов~~ вспомогательных материалов, что нас больше не запугать всякими метриками и символами Кристоффеля. Напротив, теперь нам будет о чем рассказать на посиделках с друзьями и родственниками щеголяя терминологией, которая способна свести любое шумное и веселое мероприятие к неловкому молчанию. А еще подобными знаниями можно впечатлять девушек - ничто так не вызывает интерес у противоположного пола, как страстные разъяснения физики кротовых нор.

Разумеется, когда вы принесете на свидание в ресторан небольшую маркерную доску, уровень эпатажа пригвоздит леди на месте. Пока официант не начал неуверенно мямлить про недопустимость вашего аксессуара, выпалите заблаговременно рассчитанный и заученный заказ (ведь вы заранее дома решили эту задачу многомерной оптимизации с количеством калорий, градусом алкоголя и ценой в качестве параметров). Избавившись от официанта, немедленно инициируйте социальный протокол: озвучьте приветствие, поинтересуйтесь состоянием здоровья родителей собеседницы, восхититесь внешним видом волос и ногтей девушки. Несомненно, мимика, жестикуляции и вывод темы разговора на род ваших занятий тоже должны быть заранее отрепетированы - существа женского пола не прощают нерешительности и своим хладнокровием и непримиримостью могут соперничать с диссертационной комиссией.

И вот она спросила, чем вы занимаетесь. Сощурив глаза и подняв подбородок, отдекламируйте громко и лаконично: "Познаю истину. С помощью точных и естественных наук." Голос отдавший эхом в каждом уголке ресторана создаст торжественную тишину, и все внимание будет приковано к вашему столику. Знайте, девушки любят быть в центре внимания. И конечно, они любят жертвы. И ритуалы. Так что превозмогание себя от интроверта-социопата расценится как смелый шаг и хорошая жертва. Вы уже заметили, что девушки во многом схожи с богами Хаоса - как всегда, проработанный лор фантастики находит прикладной аспект в повседневной жизни и социальной психологии.

Она говорит: "как интересно" - ловушка захлопнулась. Рассказ о настройке ssh-протокола в убунте мы оставим на знакомство с ее родителями, а начнем лучше с таинств космоса. Механикой звезд и планет не впечатлить ни одну даму, к тому же есть риск попасть впросак, ведь они часто занимаются выявлением корреляционных зависимостей состояния небесной сферы и неизмеримых энергетических потоков человеческой психики - опасная тема. Посему, лучше будет обсуждение таких таинственных моделей и явлений как кротовые норы и черные дыры, а именно, интересно рассмотреть поведение света под влиянием этих удивительных тел. Доскональный вывод геодезии в окрестности массивных космических объектов показывает самца выносливым, внимательным и аккуратным.

Отъев некоторую часть еды из своей тарелки, запишем на доске выражение для интервала в метрике Шварцшильда

$\begin{align} & \mathrm{d} s^2 = -A \mathrm{d} t^2 + A^{-1} \mathrm{d}r^2 + r^2\left(\mathrm{d}\theta^2 + \sin^2\theta\mathrm{d}\phi^2\right) \\ & A = 1-\frac{R_s}{r}\\ & R_s = \frac{2GM}{c^2}=\{\text{natural units}\} = 2M \end{align}$

Комментируйте свои действия, используйте сокращенные записи и переобозначения. Пошутите про геометрическую систему единиц. Например, "сколько километров весит Солнце?" - хорошая шутка. Девчонки любят хорошие шутки. А "чему равен твой возраст в метрах и масса в километрах" - плохая шутка. Применяя слова "возраст" и "масса" по отношению к леди, вы подвергаете себя смертельной опасности.

$\begin{align} & \mathrm{d} s^2 = -A \mathrm{d} t^2 + A^{-1} \mathrm{d}r^2 + r^2\left(\mathrm{d}\theta^2 + \sin^2\theta\mathrm{d}\phi^2\right) \quad//:-\mathrm{d}\tau^2\\ \theta = \pi/2 \\ \frac{\mathrm{d}x}{\mathrm{d}\tau} = \dot x\\ & 0 = A \dot t^2 - A^{-1} \dot r^2 - r^2 \dot \phi^2 \end{align}$

Преобразования прозрачны: сохранение углового момента позволяет избавиться от одной переменной, а формулы переписаны в терминах 4d-скоростей. Вот только барышня замечает удивительное исчезновение ds. Похвалите ее за внимательность. Девушки любят когда их хвалят. Затем напомните, что фотоны не испытывают времени. Споры о том, как и почему фотон по своим представлениям проходит нулевое расстояние за ненулевое время по данным внешнего наблюдателя, могут послужить хорошим топливом для страсти на годы вперед, так что пока оставьте мысль тлеть в ее голове. Девушки любят думать мысли.

$\begin{align} & A \dot t^2 - A^{-1} \dot r^2 - r^2 \dot \phi^2 = 0 \quad //\cdot A\\ & A^2 \dot t^2 - A r^2 \dot\phi^2 = \dot r^2 \\ A\dot t = e\\ r^2 \dot\phi = l\\ \frac{\mathrm{d}r}{\mathrm{d}\phi} = r^{\prime}\\ &e^2 - \frac{Al^2}{r^2} = \dot r^2 = \frac{\dot r^2 }{\dot\phi^2}\dot\phi^2 = r^{\prime 2}\frac{l^2}{r^4} \end{align}$

Все взгляды прикованы к доске. Администрация ресторана больше не пытается придумать способ вас спровадить, ведь никто не дебоширит и не ругает за пережаренный стейк - все тихо пучат глаза на доску, слушают объяснения и заказывают все новые порции шотов. Девушка сидит довольная и потягивает коктейль. Молчит, значит все понимает. Видно все же в художественном университете хорошая матподготовка. За сольфеджио стоит добротная волновая физика и численный анализ в нэшвиллской системе счисления. К тому же, вы ей заблаговременно скинули предыдущую статью, так что она признала введенные энергию и угловой момент на единицу массы покоя. И раз статья не спугнула, значит она - та самая.

$\begin{align} & e^2 - \frac{Al^2}{r^2} = r^{\prime 2}\frac{l^2}{r^4}\\ & r = \frac{R_s}{u},\quad r^{\prime} = \frac{R_s u^{\prime}}{u^2},\quad A = (1-u)\\ & e^2 - \left( \frac{lu}{R_s} \right)^2 (1-u) = \left( \frac{lu^{\prime}}{R_s} \right)^2\quad //\frac{\mathrm{d}}{\mathrm{d}\phi}\\ & - \left( \frac{l}{R_s} \right)^2 (2uu^{\prime}-3u^2 u^{\prime}) = \left( \frac{l}{R_s} \right)^2 2u^{\prime}u^{\prime\prime}\quad //:\frac{2l^2}{R_s^2}u^{\prime}\\ &u^{\prime\prime} = \frac 3 2 u^2 - u \end{align}$

Если после того, как вы закроете колпачок маркера тишину будут нарушать лишь прерывистые всхлипывания из-под удаленных столиков, громко огласите: "таким образом, мы получили уравнение зависимости радиальной составляющей движения фотона в окрестности стационарной черной дыры от угловой", тогда зрительный зал удостоит вас овациями.

Чтобы вдохнуть в формулы жизнь нужна визуализация. Согласно опросам, самым сексуальным языком программирования является Julia. Опрос проводился среди джулистов, при условии, что нельзя называть такие дары Слаанеш как Lisp или Prolog. Пока включается ноутбук, разогревается интерпретатор и подключаются пакеты, можно опрокинуть парочку коктейлей.

Код

using Plots, Interact
# для дифуров
function rk4(f, x, y, h)
    k1 = h * f(x       , y        )
    k2 = h * f(x + 0.5h, y + 0.5k1)
    k3 = h * f(x + 0.5h, y + 0.5k2)
    k4 = h * f(x +    h, y +    k3)

    return y + (k1 + 2*(k2 + k3) + k4)/6.0
end

function rhs(ϕ, u)
    dvdϕ = 1.5*u[1]^2 - u[1]
    [ u[2] dvdϕ ]
end

function plotter(rs, x, y, dxdt, dydt)
    
    A = range(0, stop = 2π, length=128) # рисуем кружочки
    plot(rs*cos.(A), rs*sin.(A), line=(2,:dash,:black),legend=false )
    plot!(1.5rs*cos.(A), 1.5rs*sin.(A), line=(2,:dot,:gray) )

    y += 0.5sqrt(27)*rs
    r = hypot(x, y)
    Phi = range(atan(y/x), stop = 8π, length = 1024)
    dϕ = step(Phi)
    drdt = (dxdt*x + dydt*y)/r
    dϕdt = (dxdt*y - dydt*x)/r^2
    drdϕ = hypot(drdt, r*dϕdt)
    
    function solv_step(ϕᵢ, u0)
        res = rk4( rhs, ϕᵢ, u0, dϕ )
        # не пускаем траекторию дальше 15rs
        if 1/res[1] > 15# || 1/res[1] < 1
            res = u0
        end
        return res
    end
    
    solver(u0) = [ u0 = solv_step( ϕᵢ, u0 ) for ϕᵢ in Phi ]
    
    U = vcat( solver([rs/r rs/drdϕ])... );

    R = rs ./ U[:,1]
    X = R.*cos.(Phi)
    Y = R.*sin.(Phi);
    plot!(X, Y, xlim = (-3,5), ylim = (-3,3), line = (2,:blue) )
end

Для начала, предоставьте пассии интерактив. Пусть она поварьирует начальные параметры движения луча света с помощью ползунков. Девушки любят манипулировать.

@manipulate for y in -0.5:0.01:0.5,  x in 1:10, dx in 0:0.1:5, dy in 0:0.1:5
    plotter(1.0, x, y, dx, dy)
end

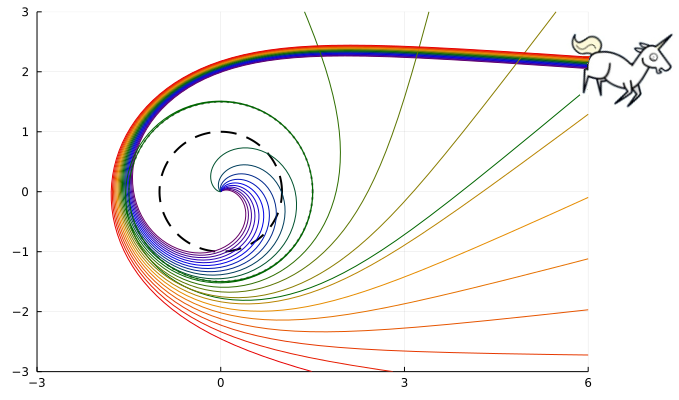
Луч загибается в изящную спираль, скользя по пунктиру фотонной сферы и падая за безвозвратную штриховую грань горизонта событий. Фотонная сфера - неустойчивая орбита. Луч либо сворачивает в небытие, либо возвращается в космос самым причудливым образом. Или же будет достаточно долго переходить между подуровнями-орбитами. Забавно, что фотонная сфера Шварцшильдовской черной дыры имеет радиус равный ровнехонько полутора радиусам горизонта событий. Один с половиной до неприличия не примечателен с точки зрения нумерологии, что вызывает подозрения и тревогу. К слову, девушки любят нумерологию.

Код

function trajectory(rs, x, y)
    
    function solv_step(ϕᵢ, u0)
        res = rk4( rhs, ϕᵢ, u0, dϕ )
        if 1/res[1] > 15# || 1/res[1] < 1
            res = u0
        end
        return res
    end
    
    solver(u0) = [ u0 = solv_step( ϕᵢ, u0 ) for ϕᵢ in Phi ]

    y += 0.5sqrt(27)*rs
    r = hypot(x, y)
    Phi = range(atan(y/x), stop = 128π, length = 5096)
    dϕ = step(Phi)
    U = vcat( solver([rs/r rs/y])... ); 
    # лучи направлены горизонтально

    R = rs ./ U[:,1]
    R.*cos.(Phi), R.*sin.(Phi)
end

rs = 1.0
A = range(0, stop = 2π, length=128)
# last photon orbit
lpo = 0.055031142005 # номералогея
Ys = range(lpo-0.1, stop = lpo+0.1, length = 21)
Ysa = range(lpo-1, stop = lpo-0.2, length = 11)
Ysb = range(lpo+0.2, stop = lpo+0.5, length = 10)
Ys = vcat(Ysa, Ys, Ysb)

P = palette( :darkrainbow, length(Ys) )

anim = @animate for (i, y) in enumerate(Ys)

    plot(rs*cos.(A), rs*sin.(A), line=(2,:dash,:black),legend=false)
    plot!(1.5rs*cos.(A), 1.5rs*sin.(A), line=(2,:dot,:gray) )
    plot!(xlim = (-3rs,6rs), ylim = (-3rs,3rs) )
    
    X, Y = trajectory(rs, 12, y)
    plot!(X, Y, line = (3, P[i]) )
end

gif(anim, "photon_orbits.gif", fps = 4)

Непреодолимость радиуса Шварцшильда заворачивает свет в спираль, заключая переносимую им информацию на поверхности черной дыры. На веки вечные. Оставшаяся часть изгибается причудливым образом, позволяя обнаружить эту таинственную космическую линзу. Но интересно взглянуть пристальней на фотонную сферу. Для этого направим на нее интенсивный источник света

В общем, выходит любопытная оптическая система: большая часть света ускользает внутрь и издалека будет видеться черный диск, причем больший чем фотонная сфера. Также будет линзирование и множественные изображения. Однако, куда интересней, что в зависимости от близости фотона к последней фотонной орбите, он может пройти несколько подорбит, прежде чем закрутиться по спирали в горизонт событий или выйти на бесконечность. По мере приближения к пределу, когда фотоны пересекают точный критический радиус орбиты, они будут вращаться бесконечное число раз. И наоборот, с точки зрения удаленного наблюдателя весь фон будет отображен на экспоненциально более тонкие кольца. Для каждого из этих путей свет достигнет наблюдателя немного ближе к краю тени черной дыры. Таким образом, наблюдатель увидит всю Вселенную, бесконечно повторяющуюся вблизи краев черной дыры.

Во-вторых, горизонт событий самой черной дыры будет многократно отображаться экспоненциально более тонкими кольцами, только внутри радиуса захвата фотонов. Поэтому любой объект, падающий, скажем, вместе с веществом аккреционного диска к черной дыре, можно многократно наблюдать все ближе и ближе к оптическому краю. Вся Вселенная отражена в экспоненциально меньших фрагментах, вплоть до квантового предела. Это невероятно красиво. Девушки любят красоту. Не упустите момент констатировать, что барышня красива. Но не добавляйте при этом "как черная дыра".

В принципе, теперь достаточно обернуть нашу окружность по углу тета, чтобы получить сферу

или показать заранее-собранный рендер, может даже с метрикой Керра для вращающейся черной дыры

Всегда полезно посмотреть на задачу под другим углом. А если позволяет симметрия, от угла можно избавиться как от одного из измерений. Тогда сфера черной дыры вырождается в окружность, а искривление пространства умещается в наглядную диаграмму

Если смотреть на изображение достаточно долго, то непременно возникнет желание добавить симметричное решение, соединив горловины двух таких воронок. В одну входит, из другой выходит. Черные и белые дыры. Только не произносите всуе "мост Эйнштейна-Розена", иначе девушка испугается, что вы хотите пересмотреть с ней звездные врата и мстюнов, а потом пройти кооператив в Portal 2. Да и ничего интересного в этом решении нет - от разрушительной гравитации не спастись, высок риск застрять между двумя горизонтами, да и белых дыр никто не видел. Куда интересней, если червоточина стабильна и не вытягивает путешественника в кровавое спагетти. Например, вариант в метрике Эллиса-Бронникова:

$\mathrm{d}s^2 = -\mathrm{d}t^2 + \mathrm{d}\ell^2 + r^2(\mathrm{d}\theta^2 + \sin^2\theta\mathrm{d}\phi^2) \\ r = \sqrt{\rho^2+\ell^2}$

Горловина со сферической симметрией соединяет два участка плоского космоса. Или две разные вселенные - поди разберись как устроены пути в гиперпространстве. А как эта штука выглядит? То есть, по нашему, какова геодезия путешествующих в ее окрестности фотонов? Те посетители ресторана, что еще не расползлись, недоуменно пожимают плечами. Окей, всем известно, что инерционное движение стремится минимизировать путь. То есть, срезай всегда по прямой, даже если пространство кривое:

$\int_{\gamma} d s=\int_{\gamma} d \lambda \sqrt{g_{\mu \nu} \dot{x}^{\mu} \dot{x}^{\nu}}\\ \dot x^\mu = \frac{\mathrm{d}x^\mu}{\mathrm{d}\lambda}$

γ - траектория, g - тензор метрики, х - вектор в пространстве-времени, λ - афинный параметр изменяющийся вдоль геодезической линии (в простонародье зовется "временем"). Любой первокурсник может записать лагранжиан в этих обозначениях, но подобная живность не встречается в столь престижных трапезных: их можно выловить только в кабаках и барах. Посему запишем сами:

$L = \frac 1 2 g_{\mu \nu} \dot{x}^{\mu} \dot{x}^{\nu}$

Все это хорошо и замечательно, но уравнения Гамильтона в данной ситуации будут проще, нежели уравнения Эйлера-Лагранжа. Лишь вспомним преобразование Лежандра:

$H = p_\mu x^\mu - L\\ p_\mu = \frac{\partial L}{\partial\dot x^\mu}\\ H = \frac 1 2 g_{\mu \nu}p_\mu p_\nu$

Украдкой взгляните на свою главную зрительницу - обычно на этом этапе игр с ко- и контрвариантными векторами несколько верхних пуговиц на блузке уже расстегнуто. Промочим горло Лонг-Айлендом и запишем супер-гамильтониан в метрике Эллиса-Бронникова, для которого будут решаться уравнения Гамильтона:

$H=\frac{1}{2}\left(-p_{t}^{2}+p_{\ell}^{2}+\frac{p_{\theta}^{2}}{r^{2}(\ell)}+\frac{p_{\phi}^{2}}{r^{2}(\ell) \sin ^{2}(\theta)}\right)\\ \dot{x}^{\mu}=\frac{\partial H}{\partial p_{\mu}}=g^{\mu \nu} p_{\nu} \\ \dot{p}_{\mu}=-\frac{\partial H}{\partial x^{\mu}}=-\frac{1}{2} \partial_{\mu} g^{\alpha \beta} p_{\alpha} p_{\beta}\\$

И держа в уме сохраняющиеся величины, записываем окончательные уравнения движения:

$\begin{aligned} \frac{d \ell}{d t} &=p_{\ell} \\ \frac{d \theta}{d t} &=\frac{p_{\theta}}{r^{2}} \\ \frac{d \phi}{d t} &=\frac{b}{r^{2} \sin ^{2} \theta} \\ \frac{d p_{\ell}}{d t} &=B^{2} \frac{d r / d \ell}{r^{3}} \\ \frac{d p_{\theta}}{d t} &=\frac{b^{2}}{r^{2}} \frac{\cos \theta}{\sin ^{3} \theta}\\ B^2 = p_\theta^2 &+ \frac{p_\phi^2}{\sin^2\theta}\\ b = p_\phi \end{aligned}$

Надо решить систему из пяти дифурок. Их решение будет описывать путь луча света, а ведь рендеру работать с двумя небесными сферами: фоном наблюдателя и небом цели путешествия

К счастью, сообщество джулистов предоставило нам полноценный инструментарий для визуализации как в интерстелларе. Понятное дело, ведь у них есть самый могущественный в обозримой вселенной солвер для дифуров.

Установка пакета

В консоли julia нажмите клавишу "]" - инициируется режим работы с пакетами. Скачиваем незарегистрированный ThorneHole.jl:

add https://gitlab.com/ExpandingMan/ThorneHole.jl

Если каких побочных пакетов не хватает, оно будет говорить при попытке запуска, так что качаем и их

add ImageMagick
add VideoIO
add FileIO
add ImageView
add StaticArrays

По умолчанию картинки для фона берутся из папки пакета, например C:\Users\User.julia\packages\ThorneHole\KuxZ0\site_assets

Файлы с сорцами копируем в удобное место и там играем с кодом. Делаем свою первую картинку

using ThorneHole
cd(s"C:\Users\User\Desktop\ThorneHole.jl-master\test")
include("render.jl")
saveimage("img0.png", wormhole())

После недолгого гудения, можем смотреть на наш родную Землю из дальних глубин космоса

Там же можно создавать видео полета. Например, всегда хотелось взглянуть в устье червоточины изнутри:

Только считайте все заранее, потому как этот маленький маневр будет стоить нам ~14 часов процессорного шипения.

Итак, вся доска размалевана до непригодности, официанты уносят осушенные маркеры и бокалы, уборщицы расталкивают остатки посетителей, а те, что уже успели сбежать, смотрят дома кошмары про тензоры Риччи. Собеседница разморённо откинулась в кресле и томно гоняет вишенку в стакане для мартини. Может рассказать ей про силу Кориолиса? Но ей вдруг становится интересен прикладной аспект всех этих формул и картинок: живут ли червоточины только на бумаге и как ими пользоваться?

Ну, это довольно неловкие вопросы. К сожалению, все съеденное и выпитое в совокупности с возбуждением (еще бы, мы смотрели в горловину кротовой норы) сделает невозможным сдержать красноту и заикание. Так-то с черными дырами все хорошо, а вот червоточины никто не видел. Но они вполне возможны. Так что они больше научная чем фантастика. Кип Торн со своим аспирантом Майком Моррисом в 73-м переполучили решение Эллиса, которое теперь частенько называют червоточиной Морриса-Торна. Да, это тот самый Кип Торн, который приложил руку к созданию "Интерстеллара".

Особенность кротовой норы Морриса-Торна состоит в том, что для поддержания ее стабильности нужна оболочка из экзотической материи с отрицательной массой. Во вторых, она не гравитирует. Поскольку гравитация отсутствует, наблюдатель может вечно находиться в состоянии покоя в любой точке пространства червоточины, но если его привести в движение каким-либо возмущением, он будет следовать геодезической экваториального сечения с постоянной скоростью, как фотон. Это, кстати, напоминает, что в пространстве-времени искривление пространства не имеет ничего общего с гравитацией, потому как там важнее "искривление времени".

Разумеется, бывают и другие типы червоточин, и некоторым даже не нужна экзотическая материя - они живут в физике бран или взращиваются инфляцией из квантовых масштабов. Но вернемся к оригинальной версии нашей червоточины - там есть еще один интересный момент. Гомер Эллис, выводил ее в 1969 г. как решение уравнений вакуумного поля Эйнштейна, дополненное включением скалярного поля, минимально связанного с геометрией пространства-времени. Он отвергал предположение Эйнштейна 1916 года о том, что инерционная масса является источником гравитации, предлагая новые, улучшенные уравнения поля, решением которых является космологическая модель с ускоренным расширением Вселенной.

В этих уравнениях "Космологическая постоянная" заменяется чистой плотностью отталкивания гравитирующей материи, обусловленной наличием реликтовых червоточин (дренажных "туннелей") и непрерывным созданием новых туннелей, для каждого из которых отталкивание превосходит притяжение. Эти дренажные туннели связанны с частицами видимой материи, обеспечивая их гравитацию, а те, которые не связаны с видимой материей, являются невидимой "темной материей". "Темная энергия", в свою очередь, представляет собой чистую отталкивающую плотность всех дренажных туннелей. Еще одна плюшка данной космологической модели это "большой отскок" вместо "большого взрыва": инфляционное ускорение из-за отскока и плавный переход к эпохе замедляющегося наката, за которым в конечном итоге следует возвращение к экспоненциальному расширению.

Отличная мозговыносяшка, которую не осилит рядовой эйнштейно-ненавистник. Хотя мне больше нравится "большой отскок" управляемый черными дырами. Но об этом поговорим на следующем свидании...

Ссылкография

https://en.wikipedia.org/wiki/Wormhole
https://en.wikipedia.org/wiki/Ellis_wormhole
Аналитическое решение для черных дыр в статье Divergent reflections around the photon sphere of a black hole
Для рендера черной дыры есть переводная статья на хабре (How to draw a Black Hole)
Рендер черных дыр в разных метриках в жестком немецком блоге Relativistischer Raytracer
Рецепт приготовления червоточины в статье К. Торна Visualizing Interstellar's Wormhole
Статья из блога того самого джулиста https://expandingman.gitlab.io/ThorneHole.jl/
Червоточина обнесена небесными сферами, а значит нужна графика в полярных координатах: Miscellaneous transformations and projections
Еще потребуются равнопромежуточные проекции: How to Use 360° Equirectangular Panoramas for Realism in Games
Квазигравитационное линзирование в домашних условиях: Trapping light by mimicking gravitational lensing

Теги:

Хабы:

Если эта публикация вас вдохновила и вы хотите поддержать автора — не стесняйтесь нажать на кнопку

Кадрим девчонок с помощью метрики Эллиса-Бронникова

Публикации

Истории

Ближайшие события