Что мы знаем про решетчатую атаку?
Начнем с того что алгоритм цифровой подписи на эллиптических кривых (ECDSA) — это распространенная схема цифровой подписи, которую мы видим во многих наших обзорах кода. Он обладает некоторыми желательными свойствами, но также может быть очень хрупким для восстановления закрытого ключа с помощью атаки по побочному каналу, раскрывающей менее одного бита секретного одноразового номера.
ECDSA— это особая форма алгоритма цифровой подписи(DSA).DSA— это довольно распространенная схема цифровой подписи , которая определяется тремя алгоритмами: генерация ключа, подпись и проверка. Алгоритм генерации ключей генерирует закрытый и публичный ключи; закрытый ключ отвечает за создание подписей; а публичный ключ отвечает за проверку подписей. Алгоритм подписи принимает в качестве входных данных сообщение и закрытый ключ и создает подпись. Алгоритм проверки принимает в качестве входных данных сообщение, подпись и публичный ключ и возвращает значениеtrueилиfalse, указывая, является ли подпись действительной.
DSA определяется для любой математической группы, и эта схема безопасна до тех пор, пока проблема дискретного логарифмирования сложна для этой группы. Обычно используемая группа представляет собой целые числа по модулю простого числа p .
Наряду с этой группой у нас будет генератор группы g и некоторая криптографически безопасная хэш - функция H. Мы можем предположить, что p , g и H будут общеизвестны.
Генерация ключей работает, сначала случайным образом выбирая значение x из целых чисел по модулю p . Затем вычисляется значение y = g^x mod p
Закрытый ключ подписи имеет значение
x, а публичный ключ —y. Ключ подписи должен храниться в секрете, поскольку именно он позволяет делать подписи.
Алгоритм подписи создает подпись из сообщения m и секретного ключа x . Сначала генерируется случайный элемент группы k . Это известно как одноразовый номер , что важно, когда речь идет об атаках.
Затем вычисляются значения r = g^k mod p и s = ( k^-1 ( H ( m ) + xr )) mod p
Здесь k^- 1 — обратная группа, а H ( m ) — результат вычисления хэша mи интерпретация результата как целое число по модулю p .
Подпись определяется как пара ( r , s ). (Примечание: если одно из значений r или s равно 0, алгоритм перезапускается с новым значением k ).
Алгоритм проверки получает на вход подпись ( r , s ), сообщение m и публичный ключ y . Пусть ŝ = s^-1 , тогда алгоритм выдает истину тогда и только тогда , когда r , s ≠ 0 и r = ( g H ( m ) y r ) ŝ .
Эта проверочная проверка работает, потому что g^H( m ) y^r = g^H(m)+ xr = g^ks, и поэтому (g^H(m)y^r)^ŝ = g^k = r
Схема цифровой подписи считается безопасной, если ее невозможно подделать .
Не подделываемость имеет формальное криптографическое значение, но на высоком уровне это означает, что вы не можете создавать подписи, не зная секретного ключа (если только вы не скопировали уже существующую подпись, созданную из секретного ключа). Доказано, что DSA невозможно подделать при допущении дискретного журнала .
DSA определяется над математической группой. Когда DSA используется с группой эллиптических кривых в качестве этой математической группы, мы называем это ECDSA. Группа эллиптических кривых состоит из точек эллиптических кривых, которые представляют собой пары ( x , y ), которые удовлетворяют уравнению y^2 = x^3 + ax + b для некоторых a , b . Для этого сообщения в блоге все, что вам нужно знать, это то, что, используя эллиптические кривые, вы можете определить конечную группу, что означает, что вы получаете генератор группы, g (точка эллиптической кривой), и операции сложения и скалярного умножения точно так же, как вы можете с целыми числами. Поскольку они образуют конечную группу, генератор,g , будет иметь конечный порядок, p. Этот пост в блоге не будет объяснять или требовать, чтобы вы знали, как работают эти операции с эллиптическими кривыми.
ECDSA работает так же, как DSA, но с другой группой. Секретный ключ x по-прежнему будет случайным значением из целых чисел по модулю p . Теперь публичный ключ y по- прежнему вычисляется как y = g^x , за исключением того, что теперь g является точкой эллиптической кривой. Это означает, что y также будет точкой эллиптической кривой (раньше y был целым числом по модулю p ). Еще одно отличие заключается в том, как мы вычисляем значение r . Мы по-прежнему генерируем случайный одноразовый номер k как целое число по модулю p , как и раньше. Мы вычислим g^k , но опять же,g — точка эллиптической кривой, и, следовательно, g^k — тоже. Следовательно, мы можем вычислить ( x^k , y^k ) = g^k и установить r = x^k . Теперь значение s можно вычислить, как и раньше, и мы получим нашу сигнатуру ( r , s ), которая по-прежнему будет целым числом по модулю p , как и раньше. Чтобы проверить, нам нужно сделать поправку на тот факт, что мы вычислили r немного по-другому.
Итак, как и прежде, мы вычисляем значение
( g^H(m)y^r)^ŝ, но теперь это значение является точкой эллиптической кривой, поэтому мы беремx-координату этой точки и сравниваем ее с нашим значениемr.
Восстановление секретных ключей из повторно используемых одноразовых номеров NONCES
Теперь, когда мы понимаем, что такое ECDSA и как он работает, давайте продемонстрируем его хрупкость. Опять же, поскольку это схема цифровой подписи, крайне важно, чтобы секретный ключ никогда не раскрывался никому, кроме лица, подписывающего сообщение.
Однако, если подписывающее лицо когда-либо выпускает подпись, а также выпускает использованный одноразовый номер, злоумышленник может немедленно восстановить секретный ключ.
Скажем, я освобождаю подпись ( r , s ) для сообщения m и случайно обнаруживаю, что использовал одноразовый номер k .
Поскольку s = ( k^-1 ( H ( m ) + xr )), мы можем легко вычислить секретный ключ:
s = (k^-1(H(m) + xr))
ks = H(m) + xr
ks – H(m) = xr
x = r^-1(ks – H(m))
Следовательно, подписывающая сторона должна не только хранить в секрете свой секретный ключ, но и все свои одноразовые номера, которые они когда-либо генерировали, в секрете.
Даже если подписывающий держит в секрете каждый одноразовый номер
NONCES, если он случайно повторит один одноразовый номерNONCES(даже для разных сообщений), секретный ключ также может быть немедленно восстановлен.
Пусть ( r , s 1 ) и ( r , s 2 ) будут двумя подписями, созданными на сообщениях m 1 и m 2 (соответственно) из одного и того же одноразового номера, k - поскольку они имеют один и тот же одноразовый номер, значения r будут одинаковыми, так что это очень легко обнаруживается злоумышленником:
s1 = k^-1(H(m1) + xr) and s2 = k^-1(H(m2) + xr)
s1 – s2 = k^-1(H(m1) – H(m2))
k(s1 – s2) = H(m1) – H(m2)
k = (s1 – s2)^-1(H(m1) – H(m2))
После того, как мы восстановили одноразовый номер k , используя приведенную выше формулу, мы можем восстановить секретный ключ, выполнив ранее описанную атаку.
Давайте на минутку переварим это.
Если одноразовый номер
NONCESдля подписи когда-либо раскрывается, секретный ключ может быть немедленно восстановлен, что нарушает всю нашу схему подписи.
Кроме того, если два одноразовых номера когда-либо повторяются, независимо от того, что представляют собой сообщения, злоумышленник может легко обнаружить это и немедленно восстановить секретный ключ, снова нарушив всю нашу схему.
Это довольно хрупко, и это только легкие атаки!
Но существует новая атака Lattice Attack которую очень подробно и детально описали Йоахим Брайтнер и Надя Хенингер (Joachim Breitner and Nadia Heninger)
Document [PDF]: Biased Nonce Sense: Lattice Attacks against Weak ECDSA Signatures in Cryptocurrencies
В блокчейне Биткоина мы нашли некую транзакцию:
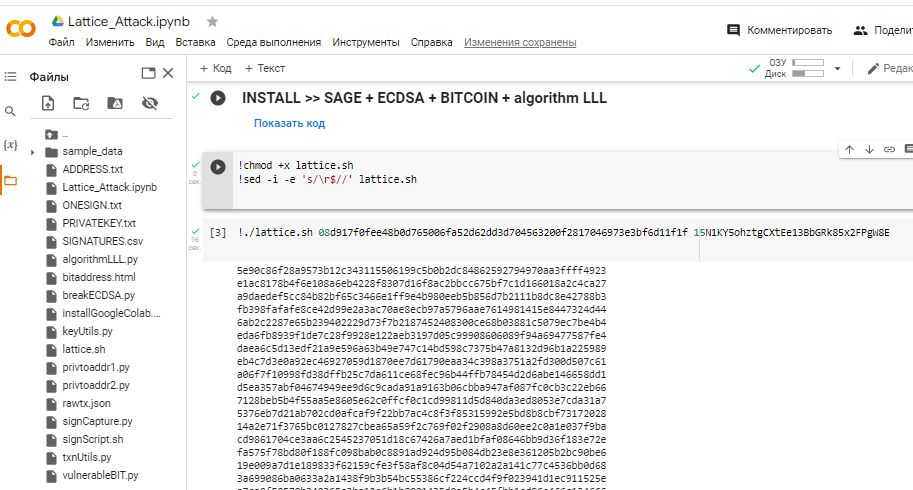
transaction: 08d917f0fee48b0d765006fa52d62dd3d704563200f2817046973e3bf6d11f1f
для Биткоин Адреса: 15N1KY5ohztgCXtEe13BbGRk85x2FPgW8E
и нам удалось размножить фейковые подписи и применить решетку
где с помощью Python-скрипта algorithmLLL.py с установкой пакетов в GOOGLE COLAB
INSTALL >> SAGE + ECDSA + BITCOIN + algorithm LLL
Нам удалось получить
Private KeyкBitcoin Walletиз одной слабой транзакции вECDSA.
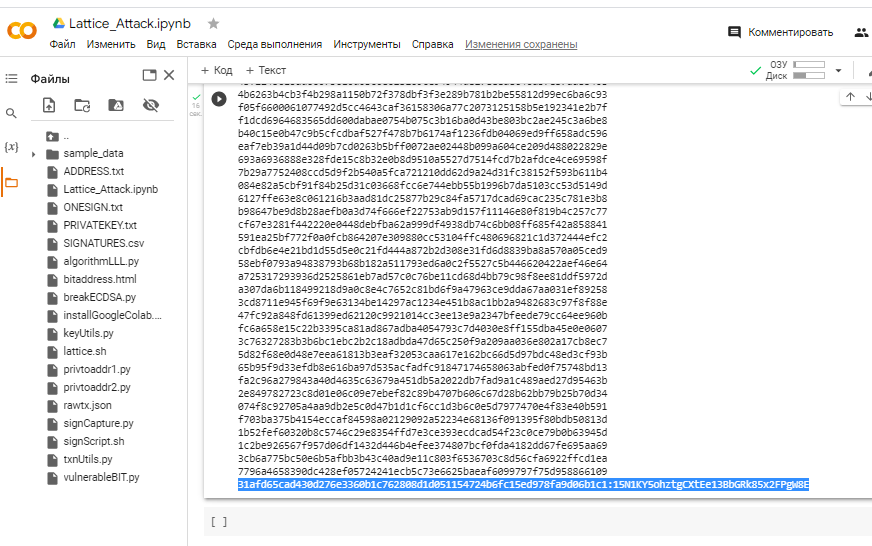



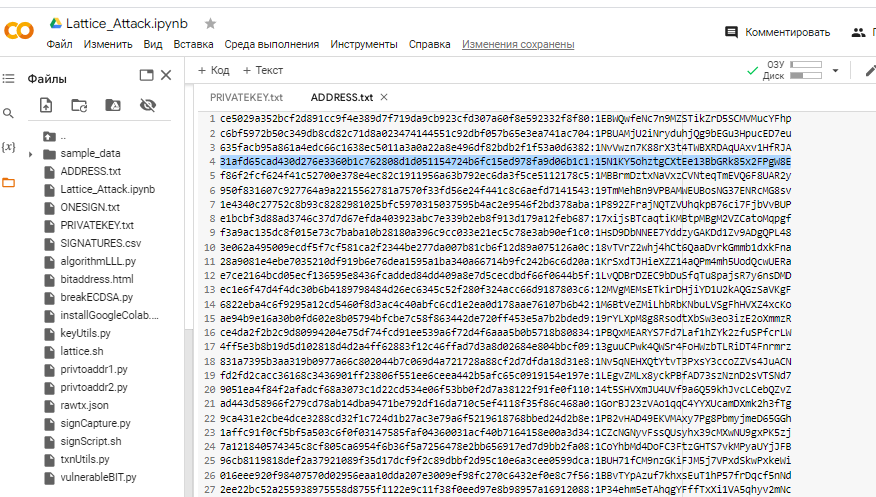
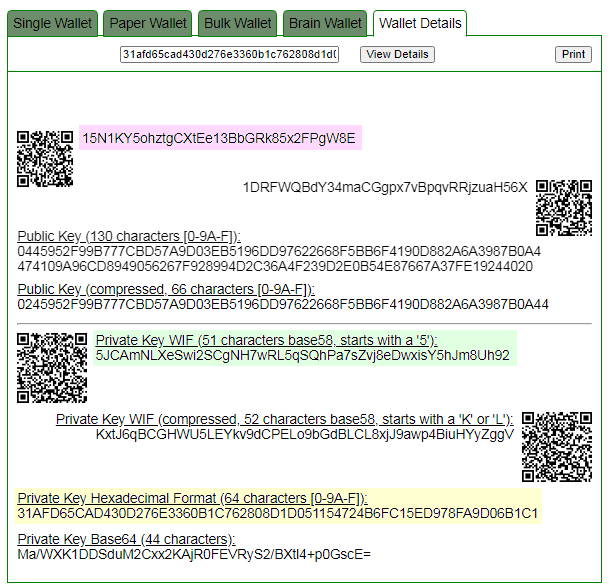
Закрытый ключ найден!
https://www.blockchain.com/btc/address/15N1KY5ohztgCXtEe13BbGRk85x2FPgW8E
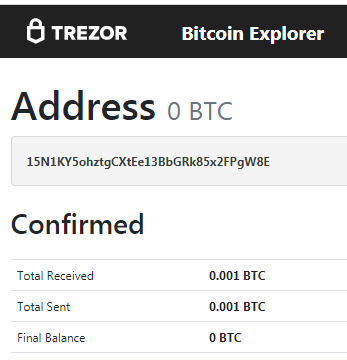
ADDR: 15N1KY5ohztgCXtEe13BbGRk85x2FPgW8E
WIF: 5JCAmNLXeSwi2SCgNH7wRL5qSQhPa7sZvj8eDwxisY5hJm8Uh92
HEX: 31AFD65CAD430D276E3360B1C762808D1D051154724B6FC15ED978FA9D06B1C1 Данный видеоматериал создан для портала CRYPTO DEEP TECH для обеспечения финансовой безопасности данных и криптографии на эллиптических кривых secp256k1 против слабых подписей ECDSA в криптовалюте BITCOIN
Видеоматериал: https://youtu.be/YP4Xj6gUcf4
Источник: https://cryptodeep.ru/lattice-attack