Продолжаем серию заметок для занятий математического кружка. Героем нашего сегодняшнего рассказа будет листок в клеточку. Этот образ стал своеобразным символом школьной математики. На одних из нас он навевает депрессивную тоску, а на иных, действует, как возбудитель, вызывая маниакальное желание что-нибудь формулировать, строить, решать и доказывать. Равнодушных "к тетрадке в клеточку", я приглашаю просто порисовать что-нибудь: косичку или лабиринт, или енота. А мы пока обсудим вот какие клеточные вопросы:
Как в тетрадке в клеточку нарисовать квадрат площадью 13 клеток так, чтобы все его вершины лежали на пересечениях сетки?
Какие, вообще, квадраты можно вписать в квадратную решётку?
А сколько существует способов нарисовать таким образом прямоугольник с заданной площадью?
Портреты каких правильных многоугольников можно изобразить в тетрадке?
Какие существуют окружности, проходящие через пересечения сетки?
В наших рассуждениях мы сосредоточимся на точках, в которых пересекаются линии сетки. Бывают такие тетрадки для художников и дизайнеров, в которых вместо клеточек, только точки. Точки эти называются узлами и образуют регулярную квадратную решётку. В этой заметке мы будем опускать эти уточняющие характеристики и просто говорить о решётке, имея в виду, что она регулярная и квадратная. Хоть мы и будем работать на обычной евклидовой плоскости, никакие точки, кроме узлов решётки, не будут концами отрезков, вершинами углов или многоугольников. Расстояние между узлами будем вычислять по Евклиду, а за единицу длины выберем один шаг решётки. Площади фигур будем измерять в единицах, определяемых минимальной квадратной ячейкой сетки.
Прямоугольники
Начиная класса с пятого, мы становимся мастерами по рисованию в тетрадке в клеточку прямоугольников с целочисленной площадью. Если площадь выражается простым числом — рисуем длинную "колбасу", шириной в одну клеточку, если составным — разбиваем на ряды и столбцы. Однако вписать в сетку прямоугольник заданной площади можно и иначе. Вот, например, какими разными способами можно построить прямоугольники площадью в 4 или в 5 клеток:
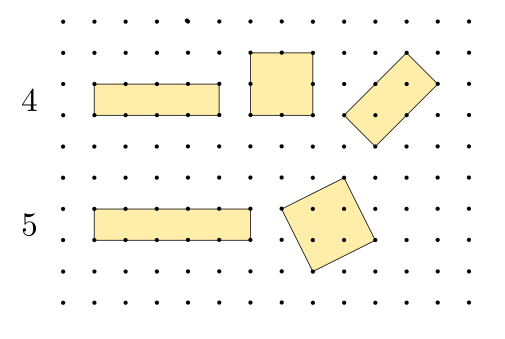
Позволив линиям наклониться, мы открыли для себя новое пространство вариантов и в нём, как оказывается, простое число 5 можно представить квадратом, а число 4 имеет три различных разложения на множители.
Давайте исследуем эти новые возможности и ответим на ряд вопросов: сколько существует способов построить прямоугольник заданной площади, используя для размещения его вершин узлы единичной решётки? Как получить исчерпывающий список таких способов? Что эта информация может сообщить о числе, которым выражается площадь? Какие числа можно представить квадратом, а какие нет?
Вспомним стандартный "школьный" подход и рассмотрим целое число , задающее площадь прямоугольника. Пусто оно имеет
делителей, включая единицу и
. В этом случае мы получаем
разных прямоугольников для чётного
и
— для нечётного. Например, у
существует 6 делителей: 1, 2, 3, 4, 6 и 12, так что из них можно составить 3 разных (неконгруэнтных) прямоугольника: 1×12, 2×6 и 3×4. В то же время, число 36 имеет 9 делителей: 1, 2, 3, 4, 6, 9, 12, 18, 36 и разлагается в 5 пар: 1×36, 2×18, 3×12, 4×9, и 6×6. Наконец, для простых площадей есть единственное представление, в виде произведения единицы на себя, и прямоугольники такой площади выглядят, как ряд клеток.
Разрешая себе использовать диагонали, мы открываем внутри регулярной квадратной решётки множество квадратных подрешёток, каждую из которых задают два натуральных числа. Вот некоторые из них:
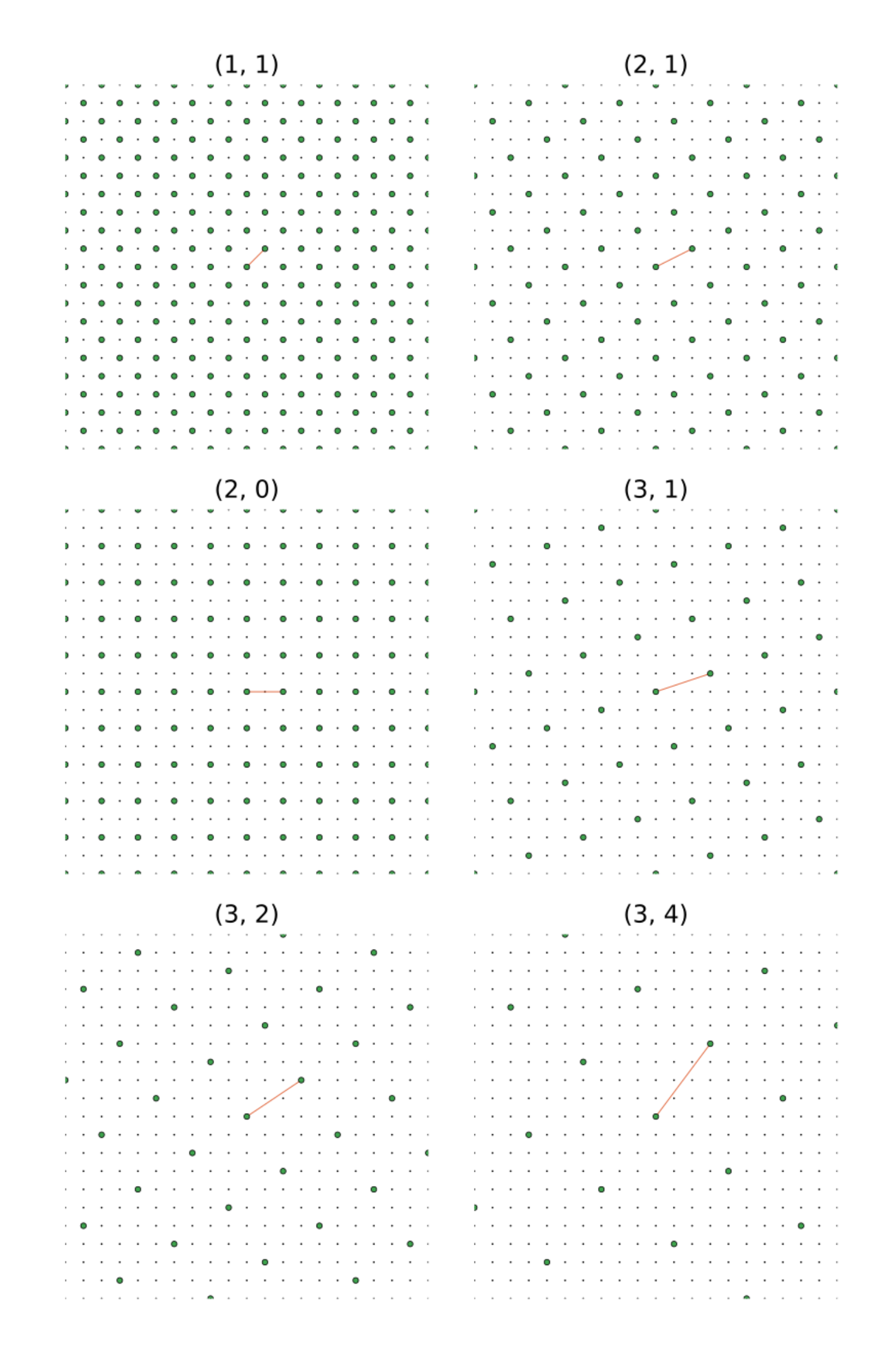
Площади ячеек в каждой подрешётке, определяемой парой , равны
. Эту площадь мы будем называть нормой подрешётки. Перебирая пары взаимно простых чисел, можно перечислить возможные площади элементарных квадратов в подрешётках: 2, 5, 10, 13, 17, 25, 26, 29, 34, 37,... Все эти числа являются суммами квадратов целых чисел. Получается, что для прямоугольника, площадь которого кратна сумме квадратов, существует способ его построения через соответствующую подрешётку.
Что объединяет суммы квадратов? Ещё в 1625 году французский математик Альберт Жирар заметил, что простые числа, дающие при делении на 4 остаток равный 1, можно представить, как сумму квадратов. Немногим позже, в 1640 году, Пьер Ферма в рождественском письме Мерсенну привёл более точную формулировку этого утверждения, а исчерпывающее доказательство было дано Леонардом Эйлером. С тех пор это свойство называют теоремой Ферма-Эйлера, или Рождественской теоремой Ферма.
Эта теорема появилась в наших рассуждениях не случайно. Она лежит в основе многих теоретикочисловых построений и существует множество её доказательств. Чтобы не перегружать эту статью, приведу вместо доказательства две ссылки на замечательные материалы по теме: статью Суммы квадратов которую А. Спивак написал для математического кружка МГУ, и видео с канала Mathologer.
Кроме того, ещё со времён Диофанта известно, что произведение сумм квадратов само является суммой квадратов. Это утверждение сейчас называется тождеством Брахмагупты-Фибоначчи. Отсюда следует общее утверждение:
Натуральное число представимо в виде суммы двух квадратов целых чисел тогда и только тогда, когда ни одно простое число вида
не входит в его разложение на простые множители в нечётной степени.
Благодаря, этому свойству, можно для любого числа выяснить, на каких решётках можно разместить прямоугольник соответствующей площади. Рассмотрим, в качестве примера, число 20. Перечислим его множители: 1, 2, 4, 5, 10, 20. Вычисляя остатки от деления простых множителей на 4, обнаруживаем, что среди множителей только три числа являются суммами квадратов: 2 = 1² + 1², 5 = 1² + 2² и 10 = 2×5 = 1² + 3². Выделим с их помощью пять разложений числа 20 на трёх подрешётках:
Таким образом, кроме трёх прямоугольников 1×20, 2×10 и 4×5, опирающихся на основную решётку, мы получили ещё пять. Итого, 8 представлений, не больше и не меньше.
На рисунке показаны все возможные прямоугольники с вершинами в узлах единичной сетки, с площадями от 1 до 20 клеточек:
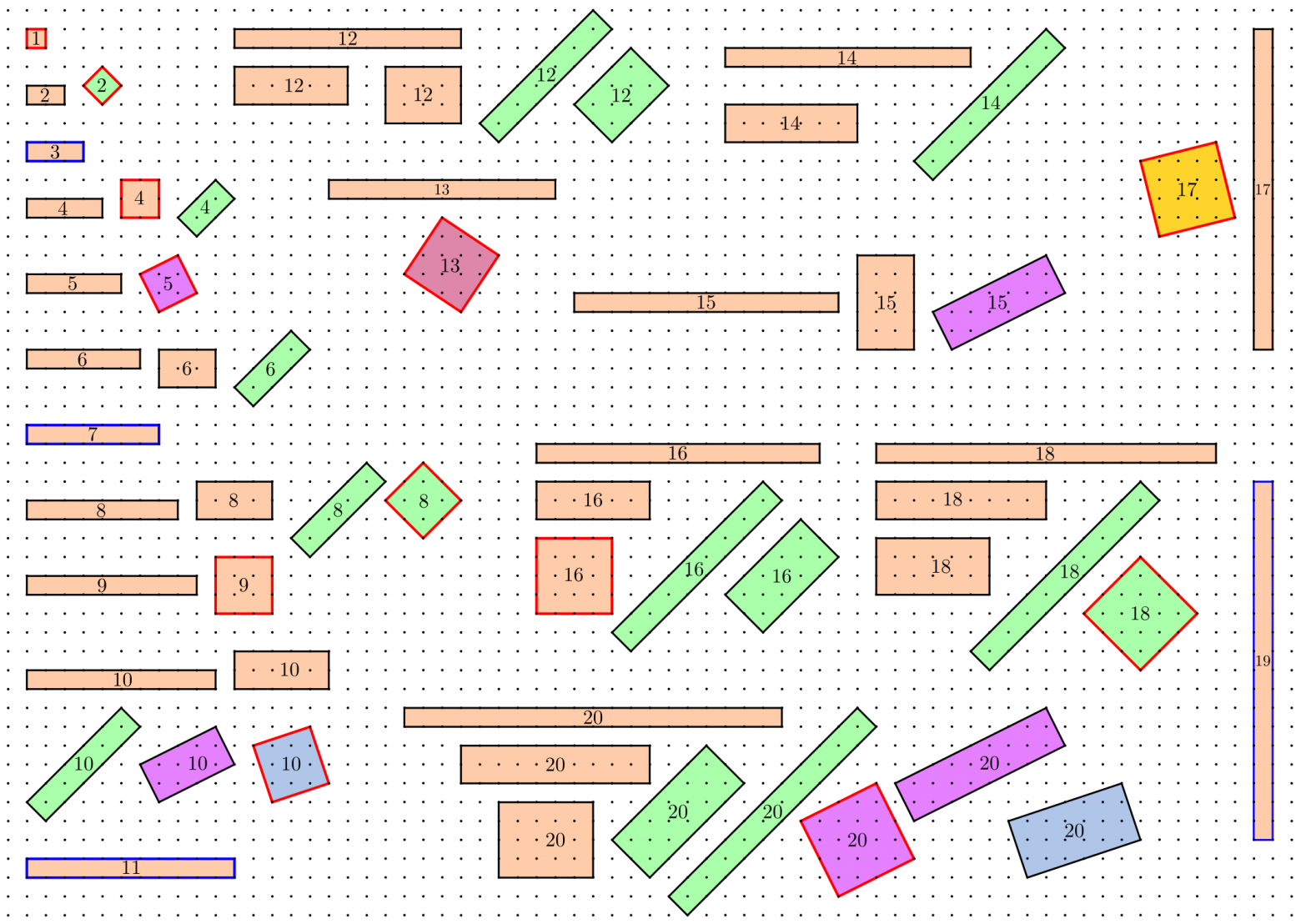
Обратите внимание на то, как много при таком построении получается правильных квадратов. Гораздо больше, чем на единичной решётке! Примечательно, что для некоторых площадей способ построения прямоугольника остаётся единственным и тривиальным: в виде цепочки единичных квадратиков, вписанных в основную решётку. Вот эти площади: 3, 7, 11, 19, 23, 31, 43, 47, 59, 67, 71, 79, 83,... Это так называемые гауссовы простые числа, то есть, такие натуральные простые числа, которые не раскладываются в сумму двух квадратов. Согласно теореме Ферма-Эйлера, все такие числа должны, при делении на 4, давать остаток 3.
Мой опыт показывает, что такое самостоятельное исследование оказывается чрезвычайно полезным для учеников 5-8 классов. Оно усиливает "чувство числа", прививает соображения о том, как можно отыскать площадь фигуры компонуя её части, и даёт опыт постановки нетривиальной задачи и обнаружения исчерпывающего решения, состоящего из нескольких вариантов. Очень рекомендую построить такой атлас прямоугольников с детьми, изучающими школьный курс математики!
Ну, а для тех, кто со школьным курсом более или менее, уже разобрался, скажу, что регулярную квадратную решётку, которую мы использовали для рисования, можно отождествить с кольцом гауссовых чисел. Это комплексные числа с целыми вещественной и мнимой частями. О кольцах мы подробно говорили в статье Теория чисел на пальцах. Подрешётки являются идеалами в этом кольце, гауссовы простые числа — простыми элементами, а построение прямоугольников – разложением на множители вещественных целых чисел в этом кольце.
Например, легко убедиться в том, что . Это разложение соответствует квадратику площадью в 5 клеток, построенному на подрешётке
. Поищите на картинке разложения гауссова числа
Квадраты соответствуют полным квадратам в гауссовых числах, которых, действительно существенно больше, чем в целых числах. Причём, многие гауссовы числа имеют более одного представления в виде суммы двух квадратов. Таковы, например, числа 25 = 5² = 3²+4² или 169 = 13² = 5²+12². Их легко выявить, распознав в них пифагоровы тройки. Применительно к прямоугольникам это значит, что прямоугольник площадью 25 клеточек можно нарисовать либо как квадрат 5×5 на подрешётке либо, как квадрат 1×1 на подрешётке
.
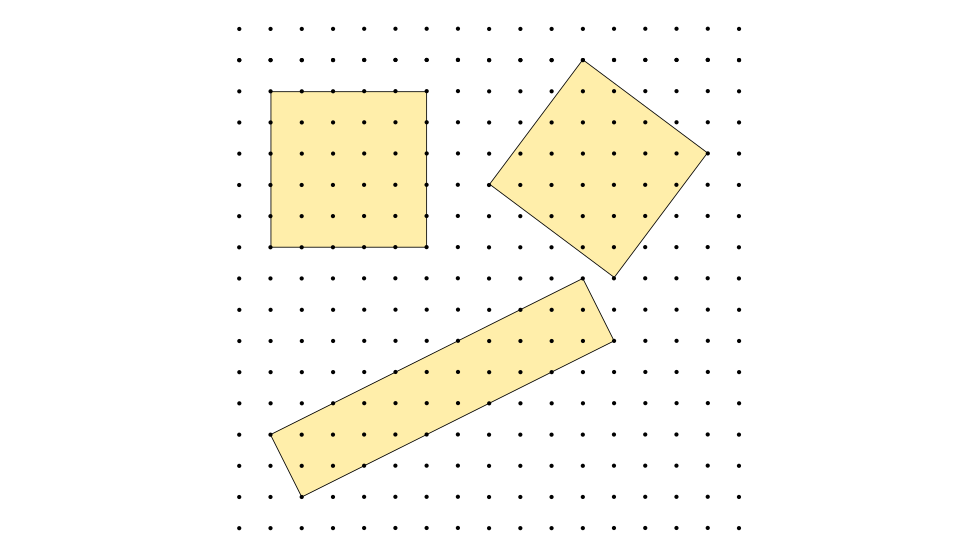
Если интересно, отыщите самостоятельно все возможные прямоугольники с площадью 100 клеточек (их должно получиться 16 штук) и 2023 клеточек (6 штук).
Правильные многоугольники
А что ещё такого правильного можно нарисовать "по клеточкам"? Уже очевидно, что прекрасно будут получаться квадраты? А как насчёт иных фигур?
Итак, мы выяснили, что внутри регулярной квадратной решётки содержится множество других подрешёток, тоже регулярных и тоже квадратных. Элементарными ячейками этих подрешёток и будут все возможные квадраты с вершинами, расположенными в узлах решётки. Их площади выражаются числами, которые могут быть представлены в виде суммы двух квадратов, либо сами являются квадратами натуральных чисел. Вот начало ряда таких чисел: 1, 2, 4, 5, 8, 9, 10, 13, 16, 17, 20, 25, 26, 29...
Таким образом, недоступными для построения останутся квадраты с площадью в 3, 6, 7, 11, 12, 14, 15, 18, 19, 21, 22, 23, 24, 27, 28, 30,... клеток. Все эти числа содержат в качестве множителя число, дающее остаток 3 при делении на 4.
Кстати, это обстоятельство позволяет имея нарисованный на бумаге рисунок, перерисовать его "по клеточкам", пропорционально увеличив его масштаб и используя одну и ту же сетку. Но масштаб увеличения, при этом, ограничен суммами двух квадратов.
А что с другими правильными фигурами: треугольниками, пятиугольниками и т.д.? Увы, кроме квадратов, вершины никакого другого правильного многоугольника в узлах квадратной решётки разместить не получится. Доказать это утверждение, достаточно просто и элегантно можно, используя наши знания о подрешётках.
Предположим, что нам удалось построить правильный многоугольник с вершинами, расположенными в узлах квадратной решётки. Каждая из сторон многоугольника является генератором своей подрешётки, а это значит, что отрезки, равные стороне, и перпендикулярные сторонам, тоже должны попадать как на узлы подрешётки, так и на какие-то узлы основной решётки. Такие отрезки называются ассоциированными.
Рассмотрим отрезки, ассоциированные со сторонами многоугольника, и ориентированные в его внутреннюю часть. В силу симметрии, все концы внутренних отрезков должны сформировать такой же правильный многоугольник, но меньше исходного. Если мы станем применять это построение многократно, то рано или поздно, получим многоугольник с длиной стороны, не превышающей минимальное расстояние между узлами решётки, и таким образом, придём к противоречию.
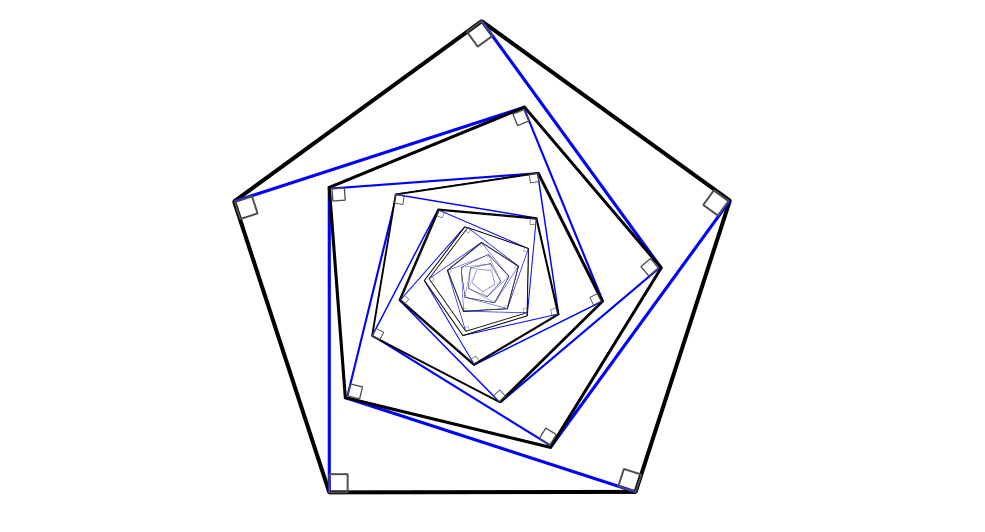
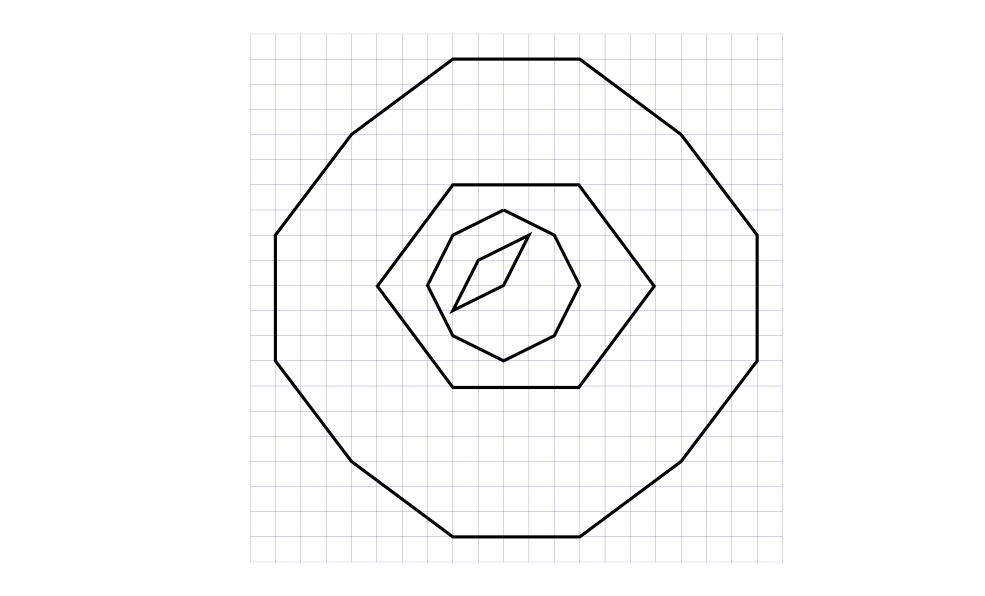
В случае треугольника этот метод не уменьшает, а увеличивает фигуру. Однако, если бы мы могли построить правильный треугольник, то нам не составило бы труда сформировать из шести его копий правильный шестиугольник, а его, как мы уже доказали, построить невозможно. Таким образом, все похожие на правильные многоугольники фигуры, нарисованные по клеточкам, могут быть лишь приближениями. Вот некоторые особо удачные приближения, вполне пригодные для рисования на уроке геометрии:
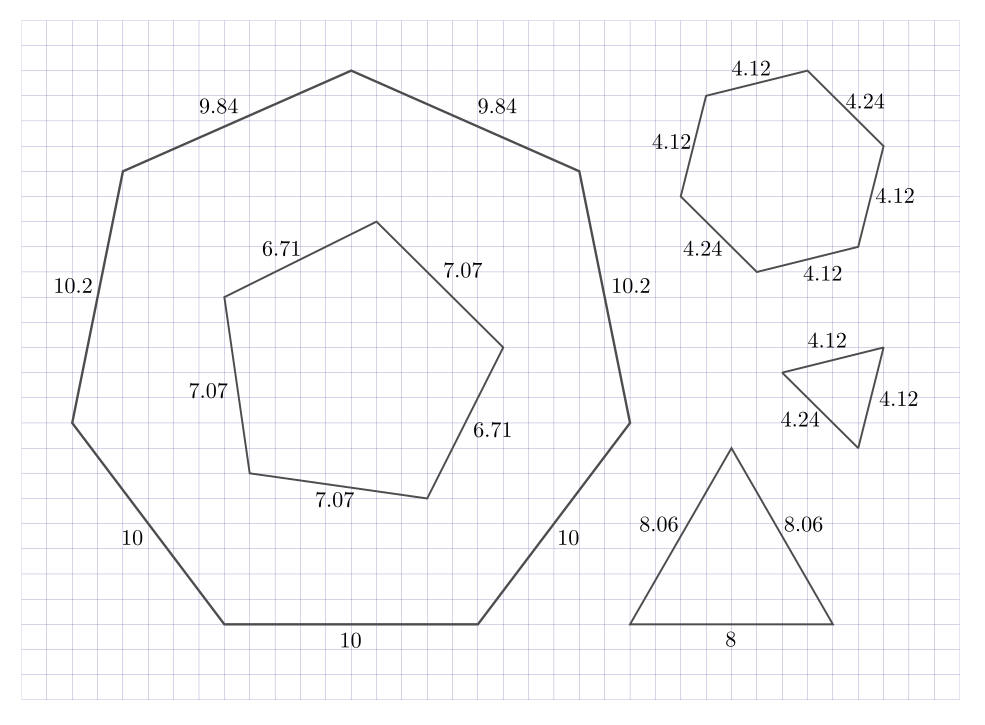
Конечно, нам остаются доступны различные равносторонние фигуры, но у них будут не равны друг другу все углы, так что правильными их назвать будет нельзя.
Невозможность существования правильных многоугольников с вершинами, расположенными в узлах регулярной квадратной решётки, само по себе, не сильно портит людям жизнь. Но это обстоятельство связано с ещё одним свойством решёток и гауссовых чисел, которое, начиная с восьмого класса, изрядно досаждает школьникам: несоизмеримость углов и тригонометрических функций — синусов косинусов и тангенсов.
Взгляните на таблицу значений тригонометрических функций для "хороших" углов. Кроме весьма особых 0°, 90°,180° и 270° нет ни одного столбца, не содержащего какой-нибудь иррациональный корень. Да и самых этих "хороших" углов очень мало: кроме тривиальных, только три: 30°, 45° и 60°. Наконец, и для этих углов синус и косинус не могут оказаться рациональными одновременно. Все же остальные углы мы не учим вовсе, потому что тригонометрия для них превращается в устрашающее нагромождение квадратных корней. В то же самое время, очень легко построить треугольник, в котором все тригонометрические функции принимают рациональные значения (как, например, в прекрасном "египетском" прямоугольном треугольнике со сторонами 3, 4 и 5), но тогда его углы оказываются несоизмеримыми с развёрнутым или прямым углом!
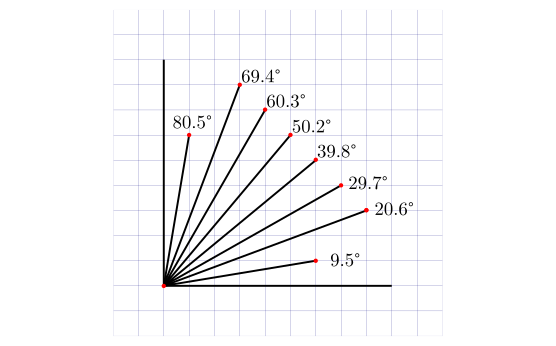
Почему это так довольно подробно разбирается в предыдущей статье из этой серии. Здесь мы только скажем, что среди углов, опирающихся на узлы решётки рациональные доли полного оборота представлены только углами, кратными 45°. Все же остальные, увы, выражаются иррациональными числами, если угловую меру определять через доли оборота.
Невозможность построения на регулярной решётке правильных многоугольников, за исключением квадратов, можно вывести из несоизмеримости тригонометрии и углов, измеряемых в долях окружности. Если вспомнить теорему Пика, которую сейчас проходят в школе, то можно заключить, что площадь любого многоугольника, с вершинами, расположенными в узлах решётки, выражается как произведение целого числа и половины площади элементарной ячейки решётки. В то же время, площадь правильного -угольника со стороной
, равна
. Тангенс угла может быть рациональным только если
(доказательство можно найти в упомянутой уже статье), так что площадь правильного
-угольника не может быть соизмеримой с половиной единицы площади, что противоречит теореме Пика.
Окружности
Итак, с правильными многоугольниками мы разобрались. А что у нас с окружностями? Точки, лежащие на одной окружности называются конциклическими. Очевидно, что нет никаких проблем нарисовать какие угодно окружности, проходящие через два или три узла решётки. А что насчёт ровно четырёх, пяти или шести конциклических точек?
Существует теорема Шинцеля, которая утверждает, что для любого натурального можно построить окружность, проходящую ровно через
узлов решётки. Статья, в которой Андрэ Шинцель приводит своё доказательство занимает чуть больше страницы и представляет образец красивой математики. Но я не хочу развивать здесь эту тему, поскольку, центры этих окружностей не попадают на решётку и их в геометрии решётки, которую мы сейчас рассматриваем, как бы, не существуют.

Давайте вместо этого зададимся вопросом а через сколько узлов может проходить окружность с центром в узле решётки?
Здесь опять имеет смысл обратиться к гауссовым числам. Пусть наша окружность с радиусом имеет центр в точке 0 и проходит через точку
, а значит,
. Мы уже знаем, что у каждого гауссова числа есть три ассоциированных с ним числа
и
. И все они имеют одинаковую норму. Это значит, если наша окружность проходит через один узел, то она обязана проходить ещё через три узла, ассоциированные с ним. Это сразу приводит к тому, что любая окружность с центром на решётке проходит через число точек, кратное четырём.
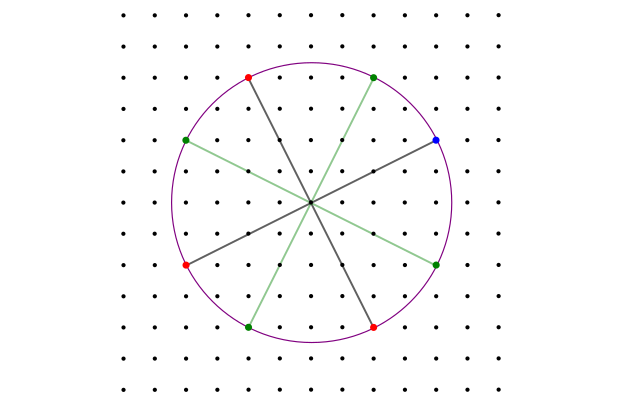
Кроме ассоциированных у гауссовых чисел есть ещё и сопряжённые числа, имеющие такую же норму. Для числа сопряжённым будет
. И если узел, лежащий на окружности не соответствует вещественному числу, то кроме ассоциированных к нему добавятся ещё и сопряжённые с ними узлы. Таким образом, у любого узла, не лежащего на вещественной или мнимой осях, есть как минимум семь конциклических узлов. Однако, их может быть и больше.
Мы уже встречали числа, имеющие более одного представления в виде суммы двух квадратов, такие, как 25 или 100. Зная простые делители некоторого числа , можно определить количество способов разложить его в виде такой суммы. Все делители
можно разбить на две группы: делящиеся на гауссовы простые числа, не делящиеся на них. Первые не имеют разложения в виде суммы квадратов, вторые -- имеют. При этом, в следствие упомянутого тождества Брахмагупты-Фибоначчи, произведение сумм квадратов само является суммой квадратов. Таким образом получается число возможных комбинаций из двух квадратов (либо соответствующих им гауссовых чисел), дающих в сумме число
где и
обозначают количество делителей числа
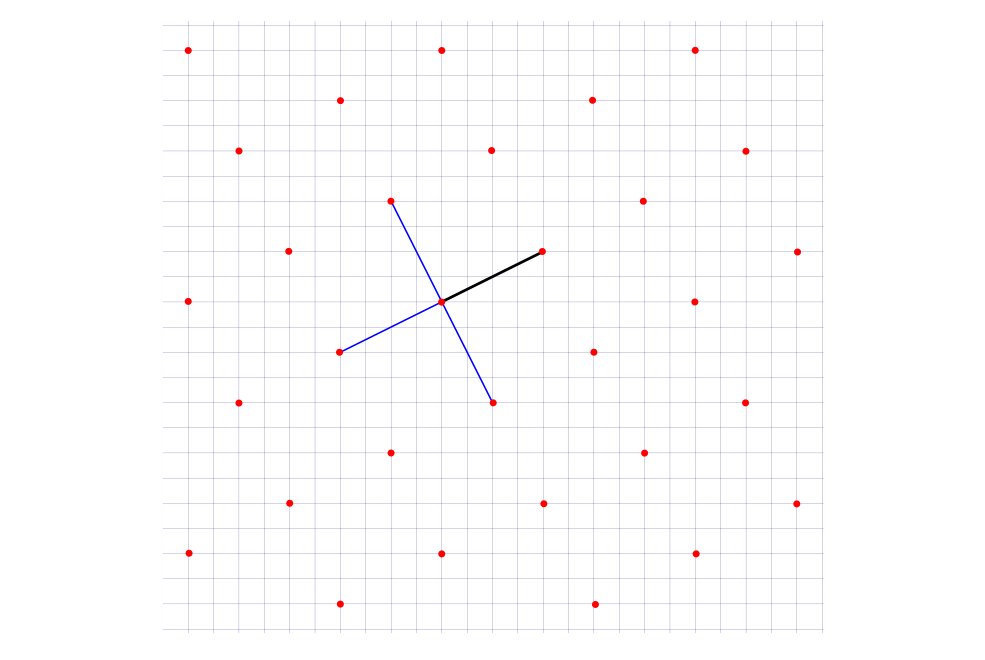
, дающих, соответственно 1 и 3 в остатке при делении на 4. Ниже приведена диаграмма точек на квадратной регулярной решётке, на которой размер узла отражает число точек, конциклических с этим узлом.

А вот похожая и даже, как кажется более простая Проблема круга Гаусса о количестве узлов решётки, попадающих внутрь круга заданного радиуса с центром в узле, до сих пор не решена.
С решётками связаны многие задачи теории чисел и теории колец. Мы рассмотрели те из них, что с одной стороны, будут понятны школьникам, а с другой достаточно интересны, чтобы превратиться в исследования и дать тем же школьникам почувствовать себя крутыми.
Предыдущие статьи серии Математическая продлёнка:
Различные заметки и материалы на Дзен-канале Онлайн-кружок математики .
