В данной статье будет рассмотрена небольшая модификация алгоритма градиентного спуска, в миллионы раз менее подверженная застреванию в локальном оптимуме, чем существующие (и с возможностью распараллеливания).
Данную статью побудило написать качество современных публикаций на тему проблем современного машинного обучения (https://habr.com/ru/company/skillfactory/blog/717360/ Wouter van Heeswijk, PhD).
Что в этом не так?
Неудовлетворительные обновления градиента политики. Например, очень малые шаги, когда зависают в локальном оптимуме, или большие шаги, из-за которых упускают наибольшее вознаграждение.
В любой формулировке мы или исследуем все пространство малыми шагами (и не пропускаем оптимум), или приходим к оптимуму большими шагами. Вообще правильнее было бы настраивать размер шагов исходя из какого-либо анализа функции ошибки с использованием БПФ, но это в следующей статье.
Алгоритмы, основанные на аппроксимации функции полезности, систематически выбирают действия с завышенной полезностью.
Залог оптимальности эвристики в отсутствии занижения функции полезности. В случае попытки сэкономить миллион\миллиард шагов алгоритма можно получить субоптимальные эвристики и не получить решение и за триллион.
Так же следует помнить, что градиентный спуск не является оптимальной эвристикой для всех типов функций ошибки (поэтому придумали обучения с моментом, и прочие трюки, которые на первый взгляд помогают быстрее находить оптимальные решения). Однако лишаться оптимальности пусть даже в некотором подмножестве множества параметров смысла нет.
Что делать(с градиентным спуском)?
Давайте напишем свою версию градиентного спуска, с множеством начальных точек и очередью с приоритетом.
В общем алгоритм выглядит так:
Инициализируем N начальных точек, для каждой из точек считаем ошибку, записываем все в очередь с приоритетом (можно делать и параллельно)
Цикл:
Достаем точку из очереди, считаем градиент ошибки, считаем изменение положения, считаем ошибку
Если точка застряла в локальном оптимуме (последние trace_len положений отличаются менее чем на эпсилон) - добавляем точку в список застрявших в локальном оптимуме, инициализируем новую точку
Если нет - помещаем точку обратно в очередь с приоритетом
Раз в несколько шагов обновляем очередь с приоритетом (можно делать и параллельно), чтобы уменьшить среднюю ошибку и увеличить оптимальность поиска.
Просто добавляем некоторое количество точек в очередь. Удаляем такое же количество точек с максимальной ошибкой.
Повторяем п. 2-5 пока не закончатся шаги или не получим требуемый уровень ошибки
Что нам это даст?
Не требует доказательств, что шанс застрять в локальном оптимуме равен примерно
, где N - количество начальных точек, P - шанс застрять в локальном оптимуме при единичном запуске
Сложность (количество шагов, требуемое для решения) будет меньше, чем N градиентных спусков (по M шагов), или M*N, но больше M+N(инициализация и спуск).
Код
python
from queue import PriorityQueue
import numpy as np
import random
from math import sqrt
##Parameters
#learning rate
dt = 0.1
#maximum step count
maxSteps = 20000
#minimum_error
minError = 0.01
##Specifical parameters
#small number to calculate derivative of target function (for using script with large object functions, like neural nets or so)
delta = 0.1
#trace length, in points
trace_len = 10
#initilal point count
N = 10000
#size of parameters space
spaceSize=[[-100,100],[-100,100]]
#for analysis purpose
GetErrorCallCount = 0
localOptimums = []
#taked from https://github.com/behnamasadi/gradient_descent/
def objective_function(vector):
z = -(4*np.exp(-(vector[0]-4)**2 - (vector[1]-4)**2)+2*np.exp(-(vector[0]-2)**2 - (vector[1]-2)**2))+4+0.2*np.sin(vector[0])+0.2*np.cos(vector[1])
return z
#we will compute exact derivative
def get_objective_function_derivatives(vector,delta,error):
res = []
initial_error = error
pos_vector = vector[0]
for n in range(len(pos_vector)):
vec = pos_vector
vec[n] = vec[n]+delta
derivative_n = -(GetError(vec)-initial_error)/delta
res.append(derivative_n)
#change to correct derivative calculation
return res
#returns normalized derivative vector
def get_error_gradient(vector,delta, error):
derivative = get_objective_function_derivatives(vector, delta, error)
#recalculate derivative, if take 0 multiply delta by ten
while all(d ==0 for d in derivative):
# print("get zero derivative")
# print(derivative)
# print(delta)
delta=delta*10
#doesnt help, return ReInitialization flag
if (delta>1000):
return [True, derivative]
derivative = get_objective_function_derivatives(vector, delta, error)
return [False, derivative]
def initGradDesc(sampleVector, priorityQueue, N):
res = []
global spaceSize
#Let's generate N random vectors with same length
for num in range(N):
#Initialize derivatives and vector randomly
pos = []
for i in range(len(sampleVector)):
pos.append(random.uniform(spaceSize[i][0],spaceSize[i][1]))
error = GetError(pos)
res.append([error, [pos]])
#Now we have N random vectors, please note that we must have normaziled data everywhere )
#lets add all those vectors in priorityQueue with our GetError Function
for x in res:
priorityQueue.put(x)
#TODO: rewrite euler integration and calculation of derivatives
#use simpliest Euler method to find change of coordinates with some derivatives
def calculateNewPosition(stateVector, error_grad, errorInit):
delta = []
#and, some trick again, trying to normalize error
delta = [x[0]+x[1]*dt for x in zip(stateVector[0],error_grad)]
return delta
#returns error for current vector as a solution
def GetError(vector):
#update call count
global GetErrorCallCount
GetErrorCallCount = GetErrorCallCount+1;
return objective_function(vector)
def getLengthBetween(item, newPoint):
l = sqrt(sum((i[0]-i[1])*(i[0]-i[1]) for i in zip(item,newPoint)))
return l
def makeGradDesc(priorityQ, point, withDetection):
global delta
errorInit = point[0]
state_vector = point[1]
#Note that point structure is [vec, derivatives_1,...,derivatives_N]
error_grads = get_error_gradient(state_vector,delta,errorInit)
error_grad = error_grads[1]
newPoint = calculateNewPosition(state_vector, error_grad, errorInit)
error = GetError(newPoint)
#merge data into one list
res = [newPoint]
curr_trace = 0;
for positions in state_vector:
res.append(positions)
curr_trace = curr_trace+1
if (curr_trace>=trace_len):
break
#calculate error
res = [error,res]
#Check for local optimum (position and cost function dont change last N steps), or we get Zero derivative and still have a significant error, initialize new point
if (withDetection and((error_grads[0] and error>minError) or (all(getLengthBetween(item, newPoint) < dt for item in state_vector)))):
localOptimums.append(res)
initGradDesc(newPoint, priorityQ, 1)
else:
if (not(withDetection) and all(getLengthBetween(item, newPoint) < dt for item in state_vector)):
localOptimums.append(res)
initGradDesc(newPoint, priorityQ, 1)
else:
priorityQ.put(res)
#main gradient descent function that runs for MaxStepCount or while minimal error is not reached
def PreformDradDesc(priorityQ, MaxStepCount,minError, withDetection):
global GetErrorCallCount
point = priorityQ.get()
error = point[0]
steps = 0
while ((abs(error)>=abs(minError)) and (GetErrorCallCount<MaxStepCount)):
steps = steps + 1
makeGradDesc(priorityQ, point, withDetection)
point = priorityQ.get()
error = point[0]
return [steps, error, point]
Ne=100
res = []
ec1 = 0
for i in range(Ne):
GetErrorCallCount = 0
#Where to store statistics about steps count/result error
research_results = []
#Queue needed for our A*
priorityQ = PriorityQueue()
initGradDesc(spaceSize, priorityQ, N+1)
minimum_error = PreformDradDesc(priorityQ, maxSteps, minError, True)
res.append([GetErrorCallCount, minimum_error[1]<minError])
ec1 = ec1+ GetErrorCallCount
print(i)
print(ec1)
print(res)
s1 = sum(item[1] for item in res)
print(ec1/s1)
print(s1/Ne)
# Mean steps: 209502.76136363635
# global optimum: 0.88
# Mean steps: 379639.8307692308
# global optimum: 0.65
# 234927.15789473685
# 0.19
# 346809.0909090909
# 0.11
res2 = []
ec2 = 0
for i in range(Ne):
GetErrorCallCount = 0
#Where to store statistics about steps count/result error
research_results = []
#Queue needed for our A*
priorityQ = PriorityQueue()
initGradDesc(spaceSize, priorityQ, 1)
minimum_error = PreformDradDesc(priorityQ, maxSteps, minError, False)
res2.append([GetErrorCallCount, minimum_error[1]<minError])
ec2 = ec2+ GetErrorCallCount
print(i)
print(ec2)
print(res2)
s2 = sum(item[1] for item in res2)
print(ec2/s2)
print(s2/Ne)
#Print results
print("Cost function calls for initialization: ")
print(GetErrorCallCount)
minimum_error = PreformDradDesc(priorityQ, maxSteps, minError)
print("Minimum error: ")
print(minimum_error[1])
print("Result point: ")
print(minimum_error[2][1][1])
print("Initial points: ")
print(N)
print("Total steps: ")
print(minimum_error[0])
print("Maximum steps: ")
print(maxSteps)
print("Cost function calls: ")
print(GetErrorCallCount)
print("Local minimums queue len: ")
print(len(localOptimums))
# for item in localOptimums:
# print(item)
Самое интересное - Objective_function:
print(objective_function([10,10])==objective_function([100,100]))
TrueИли, функция имеющая нулевой градиент при 99.9925% значениях параметров.
Результаты анализа
Да, я специально взял "простейший пример", с нулевым градиентом. И потом добавил 360000 локальных минимумов :)
z = -(4*np.exp(-(vector[0]-4)**2 - (vector[1]-4)**2)+2*np.exp(-(vector[0]-2)**2 - (vector[1]-2)**2))+4+0.2*np.sin(vector[0])+0.2*np.cos(vector[1])
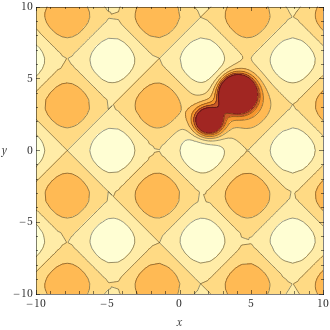
В 10 запусках из 10 был получен глобальный минимум (что уже само по себе неплохо :) ).
Детектор локальных минимумов работает как на локальный минимум, так и на плато.
Давайте запустим каждый из алгоритмов 100 раз и посмотрим, что произойдет.
Ну и сравнение простого градиентного спуска с перезапуском на плато с полным алгоритмом(я уменьшил число шагов\начальных точек до 10000 с 10 млн):
Диапазон входных параметров функции:
[[-100;100],[-100;100]]
Функция ошибки:
z = -(4*np.exp(-(vector[0]-4)**2 - (vector[1]-4)**2)+2*np.exp(-(vector[0]-2)**2 - (vector[1]-2)**2))+4+0.2*np.sin(vector[0])+0.2*np.cos(vector[1])Количество шагов: 20000
Количество начальных точек при инициализации: 10000
Полный список параметров
##Parameters
#learning rate
dt = 0.1
#maximum step count
maxSteps = 20000
#minimum_error
minError = 0.1
##Specifical parameters
#small number to calculate derivative of target function (for using script with large object functions, like neural nets or so)
delta = 0.1
#trace length, in points
trace_len = 10
#initilal point count
N = 10000
#size of parameters space
spaceSize=[[-100,100],[-100,100]]
#for analysis purpose
GetErrorCallCount = 0
Вызовов функции оценки | Результатов в глобальном оптимуме | Вызовов функции оценки на глобальный оптимум | |
Полный алгоритм с обновлением очереди | 1217770 | 94% | 13236.63043 |
Полный алгоритм (лучше, чем SOTA по ссылкам ниже) | 1950076 | 80% | 24075.012345679013 |
Только перезапуск при плато/локальном минимуме (multistart с остановкой на плато\ в минимуме) | 1966037 | 45% | 43689.71111111111 |
Просто градиентный спуск (multistart без остановки в минимуме\на плато) | 2000100 | 0% | Inf :) |
Невероятно, но простое использование очереди с приоритетом помогает добиться лучших результатов при поиске глобального оптимума при градиентном спуске.
Увы очереди с приоритетом и оптимальные эвристики не слишком часто используются разработчиками библиотек\алгоритмов связанных с поиском глобального минимума, и сравнить особо не с чем.
Но как же http://www.techmat.vgtu.lt/~art/proc/file/ZiliJu.pdf или https://aip.scitation.org/doi/pdf/10.1063/1.5089989?
Все просто, параллельный запуск N градиентных спусков даже с priority queue хуже,
чем последовательный запуск градиентного спуска, который хуже например,
последовательного запуска градиентного спуска с запуском N процессов, обновляющих данные в очереди с приоритетом, с целью понизить среднюю ошибку в последней.








