Не так давно наткнулся на статью о том, как Michael Kozakov не смог решить алгоритмическую задачу на собеседовании в Twitter. Решение этой задачи — почти в чистом виде один из самых стандартных алгоритмов на графах, а именно, алгоритм Дейкстры.
В этой статье я постараюсь рассказать алгоритм Дейкстры на примере решения этой задачи в несколько усложненном виде. Всех, кому интересно, прошу под кат.

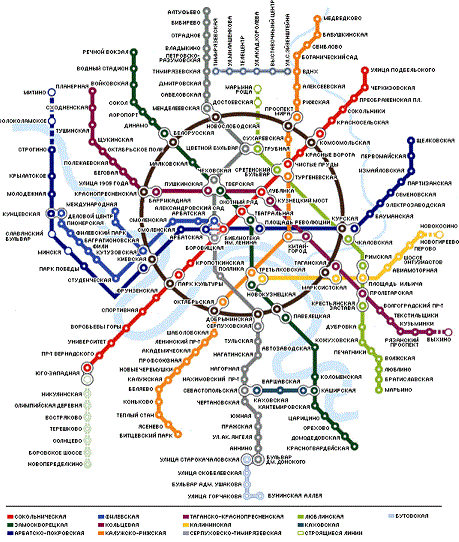В предыдущих частях цикла мы рассмотрели алгоритмы DFS и BFS, позволяющие найти путь в графе и обладающие рядом других интересных свойств. Но в жизни очень часто оказывается, что гораздо проще выглядит модель задачи в виде графа с неодинаковыми длинами ребер. Поиском кратчайшего пути во взвешенном графе мы и займемся под катом.

Добрый день, уважаемые хабровчане!
В предыдущих постах уже рассказывалось о двух алгоритмах, с помощью которых можно найти путь сквозь лабиринт: DFS и BFS. Всех, кто хочет еще немного поиздеваться над нашим лабиринтом, прошу под кат.

В предыдущем посте рассказывалось об обходе графа в глубину. Сегодня я бы хотел рассказать о не менее важном алгоритме теории графов — об обходе в ширину.
В прошлый раз мы уже научились искать какой-нибудь путь сквозь лабиринт. Всех желающих найти кратчайший путь прошу под кат.

В этой статье хотелось бы рассказать об одном из самых распространенных алгоритмов на графах — об обходе в глубину — на примере решения задачи о нахождении пути сквозь лабиринт. Всем, кому это интересно — добро пожаловать под кат!