Всем привет, в этом посте я расскажу о том, как мне удалось занять 11 место в конкурсе от компании Мерседес на kaggle, который можно охарактеризовать как лидера по количеству участников и по эпичности shake-up. Здесь можно ознакомиться с моим решением, там же ссылка на github, здесь можно посмотреть презентацию моего решения в Yandex.
В этом посте пойдет речь о том, как студент консерватории попал в data science, стал призером двух подряд kaggle-соревнований, и каким образом методы математической статистики помогают не переобучиться на публичный лидерборд.
Начну я с того, что немного расскажу о задаче и о том, почему я взялся ее решать. Должен сказать, что в data science я человек новый. Лет 7 назад я закончил Физический Факультет СПбГУ и с тех пор занимался тем, что получал музыкальное образование. Идея немного размять мозг и вернуться к техническим задачам впервые посетила меня примерно два года назад, на тот момент я уже работал в оркестре Московской Филармонии и учился на 3 курсе в Консерватории. Начал я с того, что вооружившись книгой Страуструпа стал осваивать C++. Далее были конечно же разные онлайн курсы и примерно год назад я стал склоняться к мысли о том, что Data Science — это пожалуй именно то, чем я хотел бы заниматься в IT. Мое “образование” в Data Science — это курс от Яндекса и Вышки на курсере, несколько курсов из специализации МФТИ на курсере и конечно же постоянное саморазвитие в соревнованиях.
Свою первую медальку kaggle я получил в соревновании от Сбербанка — я занял там 13 из 3000+ место, здесь решение Сбербанка со ссылкой на github. И сразу после этого я решил вписаться в соревнование от Мерседеса, до окончания которого оставалось 10 дней. Это были очень тяжелые 10 дней моего отпуска, но, во-первых, я открыл для себя много нового, во-вторых, я получил в итоге еще одну золотую медальку. И в этом посте я бы хотел поделиться тем, что я почерпнул, решая эту задачу.
Постановка задачи
На заводе Мерседес есть какая-то установка, которая тестирует новые автомобили. Время тестирования изменяется в достаточно широких пределах — ориентировочно от 50 до 250 секунд. Нам предлагается предсказать это время по более чем 300 различным признакам. Все признаки анонимизированны, но организаторы раскрыли их общий смысл. Было 8 категориальных признаков (они принимали значения вида A, XV, FD, B, ...), и это были характеристики автомобиля. Большинство признаков принимало значения 0 или 1 и являлись характеристиками тестов, которые проводились для каждой конкретной машины.
Теперь, когда общий план понятен, самое время переходить к деталям. Здесь бы я хотел сразу оговориться, что далее по тексту я не буду обсуждать тонкости ансамблирования алгоритмов или какие-то нетривиальные хитрости градиентного бустинга. Речь пойдет в основном о том, как валидироваться, чтобы не расстраиваться при открытии private leaderboard. Если отбросить все художественные подробности, мы имеем обычную задачу регрессии на анонимизированных фичах. Особенность этого конкурса состояла в маленьком (по меркам kaggle) датасете (трейн и тест примерно по 4000 объектов) и в весьма шумном таргете (боксплот таргета ниже).
Из боксплота становится очевидно, что мы столкнемся с трудностями при валидаци. Можно предположить, что на кросс-валидации нас ждет здоровенный разброс метрики по фолдам. И чтобы подлить масла в огонь, я уточню, что метрика соревнования — коэффициент детерминации (R2), который, как известно, очень чувствителен к выбросам.
Задачка привлекла столько участников прежде всего тем, что бейзлайн пишется в несколько строчек. Сделаем такой бейзлайн и посмотрим на результаты кросс-валидации:
import xgboost as xgb
from sklearn.model_selection import cross_val_score
import pandas as pd
import numpy as np
data = pd.read_csv('train.csv')
y_train = data['y']
X_train = data.drop('y', axis=1).select_dtypes(include=[np.number])
cross_val_score(estimator=xgb.XGBRegressor(), X=X_train, y=y_train,
cv=5, scoring='r2')
Вывод будет примерно таким:
[ 0.37630003, 0.43968909, 0.5886552 , 0.54800137, 0.55752035]Стандартное отклонение по фолдам настолько велико, что сравнение средних теряет смысл (в подавляющем большинстве случаев средние будут отличаться менее чем на стандартное отклонение).
Все, что будет дальше, состоит из двух частей. Первая часть простая и приятная, вызвавшая живой интерес на тренировке в Яндексе. В ней я расскажу почему большое std (Standard Deviation) – не помеха для кросс-валидации и покажу красивый и несложный подход, ликвидирующий влияние этого std. Вторая часть более сложная, но, на мой взгляд, и значительно более важная. В ней я расскажу о том, почему это не панацея, как кросс-валидация может ввести нас в заблуждение, чего имеет смысл ожидать от кросс-валидации и как к ней относиться. Итак, поехали.
Сравнение моделей на шумных данных
Для чего вообще нам нужна кросс-валидация? Когда мы решаем задачку, мы пробуем огромное количество разных моделей и хотим найти лучшую или лучшие. Таким образом, нам нужен способ сравнить две модели и достоверно выбрать из этой пары победителя. Именно в этом мы и просим помощи у кросс-валидации. Я оговорюсь, что под моделью я понимаю не просто какой-то алгоритм машинного обучения, а весь пайплайн, включающий в себя предобработку данных, отбор признаков, создание новых признаков, выбор алгоритма и его гиперпараметров. Любой из этих шагов является по сути гиперпараметром нашей модели, и мы хотим найти лучшие гиперпараметры для нашей задачи. А для этого необходимо уметь сравнивать две разные модели. Попробуем решить эту задачу.
Напомню, что значение функции потерь по фолдам кросс-валидации в задаче Мерседеса катастрофически непостоянное. Поэтому, просто сравнивая средний скор двух моделей на кросс-валидации, мы никаких выводов сделать не сможем (отличия будут в пределах погрешности). Я использовал такой подход:
1. Сделаем не одно разбиение на 5 фолдов, а 10. Теперь у нас есть 50 фолдов, но размер фолда остался прежним. В массиве scores мы получим 50 скоров на пятидесяти тестовых фолдах:
import numpy as np
from sklearn.model_selection import KFold, cross_val_score
scores = np.array([])
for i in range(10):
fold = KFold(n_splits=5, shuffle=True, random_state=i)
scores_on_this_split = cross_val_score(
estimator=xgb.XGBRegressor(), X=X_train, y=y_train,
cv=fold, scoring='r2')
scores = np.append(scores, scores_on_this_split)
2. Будем сравнивать не средний скор моделей, а то, насколько каждая из моделей лучше или хуже другой на соответствующем фолде. Или, что то же самое, будем сравнивать с нулем среднее попарных разностей результатов двух моделей на соответствующих фолдах.
Дальше я немного формализую второй пункт, но уже сейчас нужно понять, что ура, мы больше не зависим от того, что, скажем, в первом фолде у нас аутлаер, и скор там всегда очень низкий. Теперь скор на первом фолде не усредняется с остальными, он сравнивается исключительно со скором на том же фолде второй модели. Соответственно, нам больше не мешает то, что первый фолд всегда хуже второго, поскольку мы сравниваем не скор в среднем, а скор на каждом фолде и только потом усредняем.
Теперь перейдем к оценке статистической значимости. Мы хотим ответить на вопрос: значимо ли отличаются скоры наших двух моделей на наших 50 тестовых фолдах. Скоры наших моделей представляют собой связанные выборки, и я предлагаю воспользоваться статистическим критерием, специально предназначенным для таких случаев. Это t-критерий Стьюдента для связанных выборок. Я не буду перегружать пост рассуждениями о том, что гипотеза нормальности в нашем случае выполняется с достаточной точностью, и критерий Стьюдента применим — я подробно остановился на этом на тренировке в Яндексе, при желании можно посмотреть запись. Сейчас же я сразу перейду к практической части.
Статистика t-критерия имеет следующий вид:
где
– списки значений метрики по тестовым фолдам для первой и второй модели соответственно, S – стандартное отклонение попарных разностей, n – число фолдов. Здесь я хочу оговориться, что описать процедуру проверки статистических гипотез и теорию, которая за этим стоит, я в этом посте не смогу. Не потому, что это сложно для понимания, а просто потому, что, как мне кажется, пост не совсем об этом. И еще потому, что это достаточно сложно для объяснения и, сделав этот пост длиннее на два экрана, я все равно едва ли сделаю эти вещи понятнее людям, для которых они в новинку. В первых двух неделях этого курса тема проверки статистических гипотез раскрыта исчерпывающим образом, очень рекомендую: https://www.coursera.org/learn/stats-for-data-analysis/home/welcome. Итак, наша нулевая гипотеза состоит в том, что обе модели дают одинаковые результаты. В этом случае t-статистика распределена по Стьюденту с математическим ожиданием в 0. Соответственно, чем больше она отклоняется от 0, тем меньше вероятность того, что нулевая гипотеза выполняется, а средние в числителе дроби не совпали чисто случайно. Обратите внимание на знаменатель: S – это дисперсия попарных разностей. То есть, нас совершенно не интересует дисперсия скоров на фолдах для каждой модели в отдельности (то есть дисперсия
и 
), нас интересует лишь насколько «стабильно» лучше или хуже одна модель другой. Именно за это и отвечает S, находясь в знаменателе.Интересующий нас критерий реализован в библиотеке scipy в модуле stats, это функция ttest_rel. Функция принимает на вход два списка (или массива) метрик на тестовых фолдах, а возвращает значение t-статистики и p-value для двусторонней альтернативы. Чем больше t-статистика по модулю, и чем меньше p-value, тем существеннее отличия. Наиболее распространенной практикой является считать, что отличия значимы если p-value < 0.05. Давайте посмотрим, как это работает на практике:
import xgboost as xgb
from sklearn.model_selection import cross_val_score, KFold
import pandas as pd
import numpy as np
from scipy.stats import ttest_rel
data = pd.read_csv('./input/train.csv')
y_train = data['y']
X_train = data.drop('y', axis=1).select_dtypes(include=[np.number])
scores_100_trees = np.array([])
scores_110_trees = np.array([])
for i in range(10):
fold = KFold(n_splits=5, shuffle=True, random_state=i)
scores_100_trees_on_this_split = cross_val_score(
estimator=xgb.XGBRegressor(
n_estimators=100),
X=X_train, y=y_train,
cv=fold, scoring='r2')
scores_100_trees = np.append(scores_100_trees,
scores_100_trees_on_this_split)
scores_110_trees_on_this_split = cross_val_score(
estimator=xgb.XGBRegressor(
n_estimators=110),
X=X_train, y=y_train,
cv=fold, scoring='r2')
scores_110_trees = np.append(scores_110_trees,
scores_110_trees_on_this_split)
ttest_rel(scores_100_trees, scores_110_trees) Мы получим следующее:
Ttest_relResult(statistic=5.9592780076048273, pvalue=2.7039720009616195e-07)Статистика положительна, это значит, что числитель дроби положителен и соответственно среднее
больше среднего . Вспомним, что мы максимизируем целевую метрику R2 и поймем, что первый алгоритм лучше, то есть 110 деревьев на этих данных проигрывают 100. P-value значительно меньше 0.05, поэтому мы смело отвергаем нулевую гипотезу, утверждая что модели существенно различны. Попробуйте посчитать mean() и std() для scores_100_trees и scores_110_trees и вы убедитесь, что просто сравнение средних здесь не катит (отличия будут порядка std). А между тем модели отличаются, причем отличаются очень сильно, и t-критерий Стьюдента для связанных выборок помог нам это показать.На этом я бы закончил первую часть, но почему-то я уже представляю себе, как многие читатели, вооружившись этими знаниями, устроят большущий GridSearch, наделают тысячи массивов scores_xxx, сделают тысячи t-тестов, сравнивая это все с бейзлайном, и выберут алгоритм с наибольшей по модулю отрицательной t-статистикой (или положительной в зависимости от порядка аргументов ttest_rel). Друзья, коллеги, подождите, не делайте этого. GridSearch – это очень коварная штука. Давайте вспомним, что наша t-статистика распределена по Стьюденту. Это значит, что, во-первых, это случайная величина, во-вторых, даже в предположении отсутствия каких бы то ни было различий, она может принимать значения от минус бесконечности до бесконечности. Задумайтесь: от минус бесконечности до бесконечности для моделей, которые на самом деле будут давать на новых данных практически одинаковый скор! С другой стороны, чем больше значение t-статистики по модулю, тем меньше вероятность его получить случайно. То есть, например, вероятность того, что мы получим что-то больше 3 по модулю, меньше 0.5%. Но вы же делали GridSearch, проверяли несколько тысяч разных моделей. Очевидно, что даже если они ну вообще не отличались, хоть раз вы, скорее всего, эту тройку преодолеете. И примете неверную гипотезу.
В статистике это называется множественной проверкой, и существуют разные методы борьбы с ошибками при этой самой множественной проверке. Я предлагаю воспользоваться самым простым из них — проверять меньше гипотез и делать это очень осмысленно. Сейчас поясню, как я вижу это на практике.
Вернемся к нашему xgboost и попробуем оптимизировать количество деревьев. Во-первых, я призываю оптимизировать гиперпараметры строго по одному. Пусть у нас бейзлайн — 100 деревьев. Посмотрим, что происходит с t-статистикой при плавном уменьшении количества деревьев до 50:
%pylab inline
t_stats = []
n_trees = []
for j in range(50, 100):
current_score = np.array([])
for i in range(10):
fold = KFold(n_splits=5, shuffle=True, random_state=i)
scores_on_this_split = cross_val_score(
estimator=xgb.XGBRegressor(
n_estimators=j),
X=X_train, y=y_train,
cv=fold, scoring='r2')
current_score = np.append(current_score,
scores_on_this_split)
t_stat, p_value = ttest_rel(current_score, scores_100_trees)
t_stats.append(t_stat)
n_trees.append(j)
plt.plot(n_trees, t_stats)
plt.xlabel('n_estimators')
plt.ylabel('t-statistic')
То, что мы видим на графике — это хорошая ситуация. Когда у нас около 50 деревьев, ответы модели не сильно отличаются от бейзлайна со ста деревьями. При увеличении количества деревьев — отличия увеличиваются, алгоритм начинает предсказывать лучше: где-то в районе 85 мы имеем оптимум, и далее t-статистика падает, то есть алгоритм приближается к нашему бейзлайну. Посмотрев на график становится очевидно, что оптимальное количество деревьев примерно 83. А вполне можно взять 81, 82, 83, 84, 85 и усреднить. Подобного рода усреднения позволяют, практически бесплатно в смысле наших усилий, улучшить обобщающую способность и итоговый скор, я часто пользуюсь этим приемом. Я надеюсь, что из всех этих рассуждений становится понятно, что на подобных графиках нам интересен не просто глобальный оптимум, а оптимум, к которому функция плавно стремится и от которого плавно уходит. При достаточно большом количестве точек на графике мы вполне можем получить случайные всплески, которые могут быть и больше интересующего нас оптимума. Но мы отличаемся от GridSearch в том числе и тем, что будем брать не просто точку с максимальным (минимальным) значением t-статистики, а будем подходить к этому чуть более разумно.
Именно для того, чтобы была возможность смотреть на подобные графики, я призываю оптимизировать гиперпараметры по очереди. В некоторых случаях может быть оправдано перейти к 3-х мерному scatter-plot, на котором можно следить за метрикой в зависимости от двух гиперпараметров.
К сожалению, я не могу резюмировать первую часть планом вида сначала делай так, потом так, поскольку настройка гиперпараметров по кросс-валидации — дело очень тонкое и требующее постоянного анализа. Единственное, на чем я однозначно настаиваю: никогда не пытайтесь попасть в десятку — это невозможно. То, что на кросс-валидации 148 деревьев лучше, чем 149, совершенно не означает, что на тесте будет так же. Не уверены — усредняйте, потому что усреднение — это одна из очень немногих вещей, которая модель: а) точно не испортит, б) скорее всего улучшит. И осторожнее с GridSearch – этот алгоритм очень хорошо умеет создавать видимость оптимизации гиперпараметров. По меньшей мере по тем гиперпараметрам, которые вы считаете важными в данной задаче, необходимо вручную убедиться в том, что вы нашли действительно оптимальное значение, а не случайный всплеск среди белого шума.
Опасность переобучения на выбросах
Во второй части своего поста я буду рассуждать о том, что такое кросс-валидация в принципе, в чем и как она нам может помочь, а в чем не может. Предыстория такова: применив валидацию, о которой я говорил в первой части, я начал улучшать модель: что-то где-то подкручивать, отбирать фичи, добавлять новые, в общем заниматься тем, чем мы всегда занимаемся при решении kaggle. К проверке статистических гипотез я подходил очень консервативно, старался проверять их как можно меньше и как можно более разумно. Достаточно быстро я пришел к тому, что средний R2 на кросс-валидации был примерно 0.58. Как мы знаем сегодня, лучший скор на прайвате (private leaderboard) — это 0.5556. Но тогда я этого не знал, а на паблике (public leaderboard) топ был уже 0.63+, хотя и понятно было, что смотреть на чужие паблик скоры абсолютно бесполезно (leaderboard probing в этом соревновании имел небывалый масштаб). Холодный душ случился тогда, когда я сделал сабмит лучшей, по моему мнению, модели и получил на паблике 0.54, при том, что бейзлайн давал 0.55. Стало очевидно, что что-то здесь не так.
На этом моменте я бы хотел остановиться чуть подробнее. Если бы, например, это был не kaggle, а работа, я бы имел все шансы отправить такую модель в продакшн (по крайней мере попытаться это сделать). Казалось бы, что такого? У меня такая хитрая кросс-валидация, я очень аккуратно подобрал все параметры и получил высокий скор, какие могут быть вопросы? Но нужно понимать, и всегда помнить о том, о чем я тогда забыл — кросс-валидация в принципе не может оценивать перформанс модели на новых данных. На всякий случай поясню, что словом перформанс (англ. performance) я обозначаю качество работы модели в терминах выбранной метрики. Вы делаете кросс-валидацию снова и снова, выбирая только те модели, которые лучше работают на тестовых фолдах. Не на каких-то тестовых фолдах, а на совершенно конкретных и одинаковых тестовых фолдах. И даже если вы, скажем, периодически меняете random_state у Kfold, делая тем самым фолды различными, они все равно, в конечном итоге, собираются из объектов вашей обучающей выборки. И, подбирая гиперпараметры, вы натаскиваете алгоритм именно на этих объектах. Если данные хорошие, и мы все делали аккуратно, то это может привести к тому, что алгоритм будет работать чуть лучше и на новых объектах, но одинакового перформанса в общем случае ждать не стоит. А в случае, когда данные достаточно шумные, есть риск столкнуться с ситуацией, с которой столкнулся я и о которой буду рассуждать до конца поста.
Для себя я понял, что абсолютно необходимо в любой задаче иметь отложенную выборку. Я бы предложил делать так: получили задачу — сразу сделали отложенную выборку и выкинули ее из трейна. Посчитали, какой результат дает бейзлайн на этой выборке. Потом можно долго и упорно улучшать модель и наконец, когда уже самая лучшая модель готова, пришло время посмотреть скор на отложенной выборке. В случае kaggle роль отложенной выборки может играть паблик лидерборд. Но важно помнить, что чем чаще мы смотрим скор по отложенной выборке, тем хуже он оценивает перформанс модели на новых данных.
Возвращаюсь к Мерседесу. Получив на паблике скор ниже, чем у моего бейзлайна, я понял, что переобучился. Сейчас я продемонстрирую как происходит переобучение при, казалось бы, правильном подходе к подбору гиперпараметров. Для наглядности у нас будет только одна фича. Пусть истинная зависимость — синус, добавим нормальный шум и добавим нормальные же выбросы (на 15% объектов выбросы поменьше, на 4% — побольше):
import numpy as np
import seaborn as sns
import numpy as np
%pylab inline
np.random.seed(3)
X = 8 * 3.1415 * np.random.random_sample(size=2000)
y = np.sin(X) + np.random.normal(size=X.size, scale=0.3)
outliers_1 = np.random.randint(low=0, high=X.shape[0], size=int(X.shape[0] * 0.15))
y[outliers_1] += np.random.normal(size=outliers_1.size, scale=1)
outliers_2 = np.random.randint(low=0, high=X.shape[0], size=int(X.shape[0] * 0.04))
y[outliers_2] += np.random.normal(size=outliers_2.size, scale=3)
sns.boxplot(y)
plt.show()
plt.scatter(x=X, y=y)
plt.show()
Боксплот чем-то похож на то, что мы видели для таргета в задаче от Мерседеса, но выбросы присутствуют с обеих сторон.
Пусть первая тысяча объектов — это наша обучающая выборка, в вторая — тестовая. Посчитаем скоры бейзлайна на кросс-валидации:
import xgboost as xgb
from sklearn.model_selection import cross_val_score,KFold
from scipy.stats import ttest_rel
X_train = X[:X.shape[0]/2].reshape(-1,1)
y_train = y[:X.shape[0]/2]
X_test = X[X.shape[0]/2:].reshape(-1,1)
y_test = y[X.shape[0]/2:]
base_scores_train = np.array([])
for i in range(10):
fold = KFold(n_splits=5, shuffle=True, random_state=i)
scores_on_this_split = cross_val_score(
estimator=xgb.XGBRegressor(
min_child_weight=2),
X=X_train, y=y_train,
cv=fold, scoring='r2')
base_scores_train = np.append(base_scores_train,
scores_on_this_split)
Теперь, так же как мы делали в первой части, сравним с бейзлайном модели с меньшим количеством деревьев и посмотрим на зависимость t-статистики от n_estimators:
t_stats_train = []
for j in range(30, 100):
scores_train = np.array([])
for i in range(10):
fold = KFold(n_splits=5, shuffle=True, random_state=i)
scores_on_this_split = cross_val_score(
estimator=xgb.XGBRegressor(
n_estimators=j, min_child_weight=2),
X=X_train, y=y_train, cv=fold, scoring='r2')
scores_train = np.append(scores_train,
scores_on_this_split)
t_stat,p_value = ttest_rel(scores_train, base_scores_train)
t_stats_train.append(t_stat)
plt.plot(range(30, 100), t_stats_train)
plt.xlabel('n_estimators')
plt.ylabel('t-statistic')
Получим очень красивый график, из которого сделаем вывод, что оптимально брать примерно 85 деревьев:
Но посмотрим, как себя поведут эти алгоритмы на новых данных:
est_base = xgb.XGBRegressor(min_child_weight=2)
est_base.fit(X_train, y_train)
base_scores_test = r2_score(y_test, est_base.predict(X_test))
scores_test = []
for i in range(30,101):
est = xgb.XGBRegressor(n_estimators=i, min_child_weight=2)
est.fit(X_train,y_train)
scores_test.append(r2_score(y_test, est.predict(X_test)))
plt.plot(range(30, 101), scores_test)
plt.xlabel('n_estimators')
plt.ylabel('r2_score_test')
С удивлением обнаруживаем, что 85 — это далеко не оптимальное количество деревьев для нашего датасета. Виноваты в этом конечно же выбросы, и именно в такую ситуацию, как мне кажется, я попал на конкурсе Мерседес. Если вы поэкспериментируете с этим кодом, то увидите, что совершенно не обязательно оптимум на трейне будет правее оптимума на тесте, но достаточно часто их x-координата не будет совпадать.
Чтобы оценить, как сильно влияют выбросы на скор, предлагаю помучить эту строчку:
from sklearn.metrics import r2_score
r2_score(
[1, 2, 3, 4, 5, 11],
[1.1, 1.96, 3.1, 4.5, 4.8, 5.3]
)Обратите внимание на то, что если мы, например, вместо 1.1 во втором массиве напишем 1.0, скор изменится в четвертом знаке. А теперь попробуем подобраться на 0.1 ближе к нашему аутлаеру — заменим 5.3 на 5.4. Скор меняется сразу на 0.015, то есть примерно в 100 раз сильнее, чем если бы мы на столько же улучшили предсказание «нормального» значения. Таким образом, скор в основном определяется не тем, насколько точно мы предсказываем «нормальные» значения, а тем, какая из моделей случайно оказалась чуть лучше на выбросах. И становится понятно, что отбирая признаки и настраивая гиперпараметры, мы непроизвольно выбираем те модели, которые чуть лучше угадывают выбросы на тестовых фолдах, а не те, которые лучше предсказывают основную массу объектов. Это происходит просто потому, что модели, угадывающие аутлаеров, получают более высокий скор, а перформанс на основной массе объектов не очень сильно влияет на скор.
В большинстве задач, я полагаю, выбросы предсказать невозможно. Это нужно проверить, и если это так, открыто это признать. А коль скоро мы не можем их предсказать, давайте и не учитывать их при сравнении моделей. Действительно, если любая из наших моделей одинаково плохо будет предсказывать выбросы на новых данных, какой смысл тогда оценивать предсказания выбросов на кросс-валидации? Есть две стратегии поведения в таких ситуациях:
1. Давайте удалим все выбросы из обучающей выборки и только после этого будем обучать и валидировать модели. О том, как именно удалять выбросы, поговорим чуть позже, пока считаем, что как-то мы это делать умеем. Такая стратегия действительно очень сильная, победитель конкурса Sberbank Russian Housing Market Евгений Патеха валидировался именно так: youtu.be/Eo4WMlcT7uo, www.kaggle.com/c/sberbank-russian-housing-market/discussion/35684. Единственная проблема этого метода состоит в том, что зачастую выкидывание аутлаеров смещает среднее предсказание, и мы вынуждены это смещение как-то компенсировать.
2. Не будем ничего удалять из обучающей выборки, но при валидации (при вычислении значения метрики на тестовых фолдах) не будем учитывать выбросы. Я использовал именно такую схему. Мою реализацию такой кросс-валидации вы можете найти в этом репозитории, функция называется cross_validation_score_statement, определена в файле cross_val_custom.py. Еще раз, все вплоть до вызова метода fit (и включая его) мы делаем, ничего не выкидывая, затем мы делаем predict на тестовых фолдах, но метрику считаем только на объектах, не являющихся выбросами.
Как я уже говорил, получив очень низкий скор на паблике, я понял, что переобучился. Когда я начал валидироваться без аутлаеров, это переобучение сразу стало очевидно. Оказалось, что я слишком агрессивно отбирал признаки, что слишком много деревьев выращивал для своих xgboost'ов. Поправить все оказалось очень легко, я потратил примерно час на то, чтобы найти новый оптимум в пространстве гиперпараметров, и засабмитил результат. Переход к валидации без аутлаеров сделал из решения 3000+ на прайвате решение на 11 место.
Покажем, как это работает на нашем игрушечном датасете. Во-первых, необходимо определиться, кого считать аутлаером. Я считал аутлаерами объекты, на которых бейзлайн ошибается сильнее всего (ошибка out-of-fold предсказания больше какого-то порога). Порог подбирается исходя из того, сколько процентов обучающей выборки вы хотите объявить аутлаерами.
from sklearn.model_selection import cross_val_predict
base_estimator = xgb.XGBRegressor(min_child_weight=2)
pred_train = cross_val_predict(estimator=base_estimator, X=X_train, y=y_train, cv=5)
abs_train_error = np.absolute(y_train - pred_train)
outlier_mask = (abs_train_error > 1.5)
print 'Outliers fraction in train = ',\
float(y_train[outlier_mask].shape[0]) / y_train.shape[0]
Мы получим:
Outliers fraction in train = 0.045То есть 4.5% объектов объявляются выбросами. Теперь посчитаем скоры на кросс-валидации для бейзлайна, а затем будем менять количество деревьев. Только теперь выбросы при вычислении скора учитываться не будут.
# import cross_val_custom from
# https://github.com/Danila89/cross_validation_custom
from cross_val_custom import cross_validation_score_statement
from sklearn.metrics import r2_score
base_scores_train_v2 = np.array([])
for i in range(10):
scores_on_this_split = cross_validation_score_statement(
estimator=xgb.XGBRegressor(
min_child_weight=2),
X=pd.DataFrame(X_train),
y=pd.Series(y_train),
scoring=r2_score, n_splits=5,
random_state=i,
statement=~outlier_mask)
base_scores_train_v2 = np.append(base_scores_train_v2,
scores_on_this_split)
t_stats_train_v2 = []
for j in range(30, 100):
scores_train_v2 = np.array([])
for i in range(10):
fold = KFold(n_splits=5, shuffle=True, random_state=i)
scores_on_this_split = cross_validation_score_statement(
estimator=xgb.XGBRegressor(
n_estimators=j,
min_child_weight=2),
X=pd.DataFrame(X_train),
y=pd.Series(y_train),
scoring=r2_score, n_splits=5,
random_state=i,
statement=~outlier_mask)
scores_train_v2 = np.append(scores_train_v2,
scores_on_this_split)
t_stat,p_value = ttest_rel(scores_train_v2, base_scores_train_v2)
t_stats_train_v2.append(t_stat)
plt.plot(range(30,100), t_stats_train_v2)
plt.xlabel('n_estimators')
plt.ylabel('t-statistic')
Получим такой график:
Видно, что, к сожалению, это не серебряная пуля, и оптимум все равно находится не на 50 деревьях, как хотелось бы. Но это уже и не 85 как было раньше, и экстремум не такой явный, что наводит на мысли о том, что имеет смысл усреднить по количеству деревьев от 60 до 95. А сделав это, мы вполне возможно получим результат, сопоставимый с тем, который мы бы получили, если бы знали, что на самом деле нужно брать 50.
И последнее, что я хочу показать — это как в действительности меняются предсказания нашего бустинга при росте количества деревьев, благо в одномерном случае это можно сделать. Для разных n_estimators я буду строить предсказания алгоритма и склею это в gif:
X_plot = np.linspace(0,8 * 3.1415, num=2000)
est = xgb.XGBRegressor(n_estimators=70, min_child_weight=2)
est.fit(X_train, y_train)
plt.plot(X_plot, est.predict(X_plot.reshape(-1, 1)))
plt.xlabel('X')
plt.ylabel('Prediction')
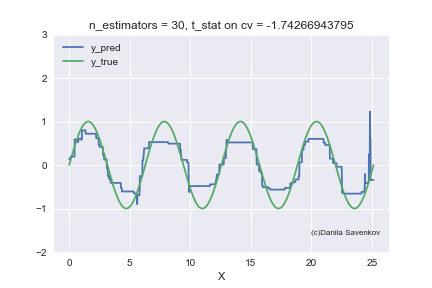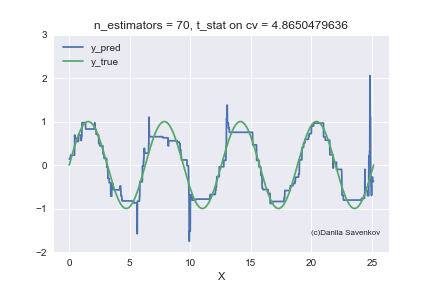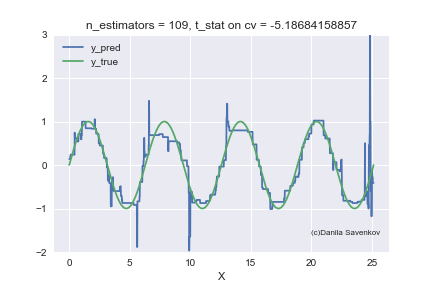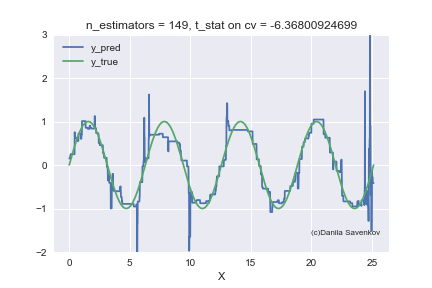
Видим как сильно мешают аутлаеры работать нашей модели. Также видим, что после примерно n_estimators=60 модель фактически перестает приближаться с исходной функции и занимается лишь тем, что переобучается на выбросах из обучающей выборки. Вспомним, что на наших «новых» данных лучше всего показывают себя 50 деревьев. А на анимации при n_estimators=60, 70, 80 t-статистика на кросс-валидации продолжает увеличиваться, и увеличивается она именно благодаря удачному попаданию в аутлаеры. Когда я сделал эту анимацию, идея обучать модели на очищенном датасете стала мне казаться еще более привлекательной. Много чего еще можно сказать, глядя на эту гифку, но не смею вас больше задерживать.
Очень надеюсь, что вы не жалеете о потраченном на прочтение этого поста