Comments 72
1) похоже что параллельные направления от тюрмы могут идти только в 1 направлении. и тогда коп догонит сбежавшего.
2) да, сможет, если сразу пойдёт в угол. тогда волк встретиться только с 1 собакой (он преодолеет половину диагонали квадрата чуть быстрее, чем собака целую сторону, так что встретиться только с 1 собакой).
2) да, сможет, если сразу пойдёт в угол. тогда волк встретиться только с 1 собакой (он преодолеет половину диагонали квадрата чуть быстрее, чем собака целую сторону, так что встретиться только с 1 собакой).
1. направления расходятся в разные стороны
2. учитывайте, что скорость собаки выше чем у волка в 1.5 раза
2. учитывайте, что скорость собаки выше чем у волка в 1.5 раза
тьфу ты, я тут что-то перепутал, что на 1.42 умножать ;) Получается, что через угол он так сходу не уйдёт. Сейчас подумаю ещё немного.
2. а что если волку посидеть у середины ребра, дождавшись пока все собаки окажутся в одной точке и затем рвануть назад, к противоположному?
Да, хороший вариант. Но давайте предположим, что собаки имеют чуточку больше мозгов и не будут толкаться тупо в одной точке.
Волк подходит к одному углу, ждет, когда все собаки там соберутся, и ломится в противоположный угол.
Ну, или даже так: волк направляется к середине стороны квадрата А. Две собаки вынуждены туда бежать из ближайших углов. Две остальные остаются в углах.
После чего волк по диагонали бежит в середину одной из прилегающих сторон Б, куда успевает лишь одна собака, поскольку волку потребуется пробежать примерно в 1,4 раза меньшее расстояние, чем второй собаке из А в Б.
После чего волк по диагонали бежит в середину одной из прилегающих сторон Б, куда успевает лишь одна собака, поскольку волку потребуется пробежать примерно в 1,4 раза меньшее расстояние, чем второй собаке из А в Б.
в первом вопросе мне не очень понятна формулировка. Если тюрма — здание и оба направления уходят от дверей тюрмы, и при этом не пересекаются, то они параллельны и представляют собой лучи. Так что коп обязан догнать приступника (он не может ошибиться с направлением). Если же направления коллинеарны и не однонаправлены, то с вероятностью в 50% догонит ;)
уточню про дорогу. это одна дорога. по ней можно поехать бесконечно на юг, или бесконечно на восток. разъехавшись в разные стороны они не пересекутся. так лучше?
вариант с 50% крайне очевиден и подойдет как решение классе в пятом. 50/50 = либо/либо.
вариант с 50% крайне очевиден и подойдет как решение классе в пятом. 50/50 = либо/либо.
1. Если коп знает через сколько времени с начала побега он начал погоню и он не дурак, то догонит.
Обоснуйте
Ну если коп начал погоню то как минимум он уже предполагает что его машина может быть быстрее. Допустим он предположил что его скорость на 1 км/ч больше чем у преступника, тогда он зная время побега может вычислить через сколько времени он сможет его догнать поехав по одной из дорог. Он начинает погоню по любой дороге, если он не догнал за это время, то разворачивается и едет по другой. В этом случае он так же исходя из предположения о скорости может вычислить за через сколько он гипотетически может его догнать.
Попробуйте вычислить.
Так как я предложил решение через предположение о разнице скорости в 1 км/ч, то задача решается элементарно. Мы просто имеем что скорость приближения равна 1 км/ч.
Соответственно если погоня началась через час после побега, а скорость копа 100 км/ч, то в одну сторону копу потребуется 99 часов, во вторую — 9900 ч (100 часов * гипотетическая скорость преступника 99 км/ч).
Практически уверен что у этой задачи есть более элегантное и более математическое решение без предположений о разнице скоростей в 1ч.
Соответственно если погоня началась через час после побега, а скорость копа 100 км/ч, то в одну сторону копу потребуется 99 часов, во вторую — 9900 ч (100 часов * гипотетическая скорость преступника 99 км/ч).
Практически уверен что у этой задачи есть более элегантное и более математическое решение без предположений о разнице скоростей в 1ч.
тут много писать.
Пусть побег совершён в момент Т
коп начинает дорого в момент времени Т+Тd
скорость преступника V
копа — V+Vd (Vd может быть любым).
соотношение скоростей копа и преступника K=(V+Vd)/V
время встречи в одном из направлений Tx1=Td/(K-1) секунд (размерность вроде сошлась)
время встречи в другом направлении Tx2=Tx1/(K-1).
То есть сделав все предположения мы получаем, что коп сможет догнать преступника за Tx1+Tx2, но не сделает этого, если ошибётся с предположением о разности скоростей.
С какой вероятностью оценка разности скоростей полицеского окажется верной?)
Пусть побег совершён в момент Т
коп начинает дорого в момент времени Т+Тd
скорость преступника V
копа — V+Vd (Vd может быть любым).
соотношение скоростей копа и преступника K=(V+Vd)/V
время встречи в одном из направлений Tx1=Td/(K-1) секунд (размерность вроде сошлась)
время встречи в другом направлении Tx2=Tx1/(K-1).
То есть сделав все предположения мы получаем, что коп сможет догнать преступника за Tx1+Tx2, но не сделает этого, если ошибётся с предположением о разности скоростей.
С какой вероятностью оценка разности скоростей полицеского окажется верной?)
Машина копа более быстрая, чем у сбежавшего чела, но коп об этом не знает.
На самом деле, я тоже думал над подобным решением, но условие задачи это решение перечеркивает.
В целом, я думаю, что оригинальное решение как раз основывается на подобном логическом заключении. С одной оговоркой. Разница в скорости может быть любой (в том числе и меньше 1км/ч).
И беря за основу, что разница в скорости 1км/ч — мы просто увеличиваем шансы того, что догонит.
Чем меньше мы будем предполагать разницу в скорости — тем больше вероятность того, что догонит. Но, 100% утверждения в этой задаче сделать нельзя.
На самом деле, я тоже думал над подобным решением, но условие задачи это решение перечеркивает.
В целом, я думаю, что оригинальное решение как раз основывается на подобном логическом заключении. С одной оговоркой. Разница в скорости может быть любой (в том числе и меньше 1км/ч).
И беря за основу, что разница в скорости 1км/ч — мы просто увеличиваем шансы того, что догонит.
Чем меньше мы будем предполагать разницу в скорости — тем больше вероятность того, что догонит. Но, 100% утверждения в этой задаче сделать нельзя.
На самом деле, конечно, коп подозревает, что его машина быстрее. Просто он не знает насколько. А в рассуждении выше фигурирует конкретное число Vd.
Можно выкрутиться так и будем считать, что Td известно (то есть, коп может оценить верхнюю границу, ну, пусть, один час).
Предположим, что Vd = 1км/ч. Проедемся, как написано выше в обе стороны. Не догнали? Ну, наверно Vd меньше. Может 0.5км/ч? Проедемся обять в обе стороны с новым Vd и соответственно пересчитанным Td.
Кажется — доказать не пытался — что для любого ненулевого Vd в итоге коп догонит, когда-нибудь.
Можно выкрутиться так и будем считать, что Td известно (то есть, коп может оценить верхнюю границу, ну, пусть, один час).
Предположим, что Vd = 1км/ч. Проедемся, как написано выше в обе стороны. Не догнали? Ну, наверно Vd меньше. Может 0.5км/ч? Проедемся обять в обе стороны с новым Vd и соответственно пересчитанным Td.
Кажется — доказать не пытался — что для любого ненулевого Vd в итоге коп догонит, когда-нибудь.
По условию коп не знает, что скорость его машины выше. Таким образом он может ехать в неправильную сторону бесконечно долго.
2. Дойдем до центра и выберем любого волка. Если волк сейчас в вершине, то выберем любую сторону около противоположной вершины. А если на какой-то стороне, то выбираем противоположную ей сторону. Заметим, что до выбранной стороны нам бежать по перпендикуляру a/2(a — сторона квадрата), а волку не менее a. Мы затратим 0.5a / V, волк 2/3 / V. Мы выиграли?
с собаками я поторопился. «играя» за собак можно предложить стратегию такую, что волк не сможет выбраться.
Строится она на том, что от волка строится перпендикуляр к каждой из сторон, а так же «наклонные» под 45 градусов к той же стороне. Получается своеобразный «прицел». Собаки могут успевать находиться в точках пересечения наклонной и стороны квадрата. Таким образом, волк не может встретиться только с 1 собакой и, насколько я понимаю конструкцию, не может «запутать» собак так, чтобы обогнать хотя бы 1 из пары.
Строится она на том, что от волка строится перпендикуляр к каждой из сторон, а так же «наклонные» под 45 градусов к той же стороне. Получается своеобразный «прицел». Собаки могут успевать находиться в точках пересечения наклонной и стороны квадрата. Таким образом, волк не может встретиться только с 1 собакой и, насколько я понимаю конструкцию, не может «запутать» собак так, чтобы обогнать хотя бы 1 из пары.
Правильно, cобаки выигрывают.
Чтобы не запутаться в построениях, можно обратить внимание, что проeкции положения собак на диагонали квадрата совпадают с проeкцией волка, а потом доказать что а) собаки могут сохранять эту ситуацию за счет 1.5 > sqrt(2), б) когда волк доползeт до границы, его встретят 2, а в углу все 3 собаки.
Чтобы не запутаться в построениях, можно обратить внимание, что проeкции положения собак на диагонали квадрата совпадают с проeкцией волка, а потом доказать что а) собаки могут сохранять эту ситуацию за счет 1.5 > sqrt(2), б) когда волк доползeт до границы, его встретят 2, а в углу все 3 собаки.
Волком по расширяющейся спирали надо двигаться, и при малейшей возможности уходить.
Решение первой задачи от havoc_a (read-only)
решение задачи 1:
пусть зэк стартует в момент времени t=0 и его движение задаётся кривой y=t (т.е. возьмём скорость равной 1)
коп стартует в момент времени t=E (естественно, предполага, что его машина быстрее, иначе какой смысл пробовать доганать?)
коп быстренько прикидывает, что ему нужно двигаться по кривой Y=(vt-E)sin(vt-E), где v — максимальная скорость его машины.
за точку 0 по оси s (пройденное расстояние) возьмём тюрму
По условию v>1 (скорость зэка мы приняли за 1), таким образом коп догонит зека, не зная точно, в какую сторону он поехал.
решение задачи 1:
пусть зэк стартует в момент времени t=0 и его движение задаётся кривой y=t (т.е. возьмём скорость равной 1)
коп стартует в момент времени t=E (естественно, предполага, что его машина быстрее, иначе какой смысл пробовать доганать?)
коп быстренько прикидывает, что ему нужно двигаться по кривой Y=(vt-E)sin(vt-E), где v — максимальная скорость его машины.
за точку 0 по оси s (пройденное расстояние) возьмём тюрму
По условию v>1 (скорость зэка мы приняли за 1), таким образом коп догонит зека, не зная точно, в какую сторону он поехал.
Решение первой задачи, опираясь на то, что скорость мента Vm равна скорости зэка Vz + константана Vc, где Vc > ε.
В обе стороны отправляем по виртуальной машине со скоростью Vv = (Vm + Vz) / 2. Т.к. мент не знает скорости зэка, лучше возьмем Vv = Vm — ε.
Мент ждет 1 секунду, потом едет за первом виртуальной машиной, и когда-то ее догонит т.к. скорость его больше этой виртуальной машины. Потом разворачивается и едет за другой. И ее догонит, по тем-же причинам. Потом снова едет за первой, потом снова за второй и так до бесконечности. Учитывая, что скорость виртуальной машины больше скорости зэка, одна из виртуальных машин когда-то его догонит, и мент когда-то догонит ту виртуальную машину, которая уже догнала / обогнала зэка. В общем, мент обязательно догонит.
P. S. Следуя этому алгоритму, мент будет на столько зол, что зэк скорей всего не выживет.
В обе стороны отправляем по виртуальной машине со скоростью Vv = (Vm + Vz) / 2. Т.к. мент не знает скорости зэка, лучше возьмем Vv = Vm — ε.
Мент ждет 1 секунду, потом едет за первом виртуальной машиной, и когда-то ее догонит т.к. скорость его больше этой виртуальной машины. Потом разворачивается и едет за другой. И ее догонит, по тем-же причинам. Потом снова едет за первой, потом снова за второй и так до бесконечности. Учитывая, что скорость виртуальной машины больше скорости зэка, одна из виртуальных машин когда-то его догонит, и мент когда-то догонит ту виртуальную машину, которая уже догнала / обогнала зэка. В общем, мент обязательно догонит.
P. S. Следуя этому алгоритму, мент будет на столько зол, что зэк скорей всего не выживет.
Еще проще — 1 км влево, 10^100 вправо, 10^200 влево, 10^300 вправо…
Вот только экспоненты тут не хватит, т.к. доля потраченного «зря» времени всегда будет не меньше некоторой константы. И если доля отличия нашей скорости от скорости преступника меньше этой константы, то мы его не догоним.
Так что едем 1! влево, 2! вправо, 3! влево и т.д.
Так что едем 1! влево, 2! вправо, 3! влево и т.д.
хорошо, но
1. ε неизвестна, может быть сколь угодно малой.
2. нет смысла гоняться за одной и той же виртуальной машиной много раз.
я делаю другое допущение, что коп примерно знает когда выбежал преступник. Ну, на уровне «не раньше, чем час назад» или «не раньше, чем год назад».
Тогда запускаем виртуальные машины стартовавшие в это время (час назад или год назад) с разными скоростями в обе стороны. Со скоростями, например, V1=Vm — ε (для какой-то фиксированной ε), V2=Vm — ε/2, V3=Vm — ε/3, и так далее. Ну и мент догоняет вначале V1 справа, потом V1 слева, потом V2 справа, и так далее. То есть на каждом втором шаге он предполагает что преступник ехал чуть быстрее, раз он его пока еще не догнал. Рано или поздно догонит…
1. ε неизвестна, может быть сколь угодно малой.
2. нет смысла гоняться за одной и той же виртуальной машиной много раз.
я делаю другое допущение, что коп примерно знает когда выбежал преступник. Ну, на уровне «не раньше, чем час назад» или «не раньше, чем год назад».
Тогда запускаем виртуальные машины стартовавшие в это время (час назад или год назад) с разными скоростями в обе стороны. Со скоростями, например, V1=Vm — ε (для какой-то фиксированной ε), V2=Vm — ε/2, V3=Vm — ε/3, и так далее. Ну и мент догоняет вначале V1 справа, потом V1 слева, потом V2 справа, и так далее. То есть на каждом втором шаге он предполагает что преступник ехал чуть быстрее, раз он его пока еще не догнал. Рано или поздно догонит…
Ну, в таких терминах всё еще проще.
Предполагаем, что он выехал влево со скоростью в 1+x раз меньше нашей, и это было за x минут до начала погони. Пытаемся догнать. Если не получилось — предполагаем, что он выехал вправо со скоростью в 1+x/2 раз меньше нашей за 2x минут до начала погони. И т.д. Рано или поздно наше предположение окажется соответствующим действительности, и мы его догоним.
Предполагаем, что он выехал влево со скоростью в 1+x раз меньше нашей, и это было за x минут до начала погони. Пытаемся догнать. Если не получилось — предполагаем, что он выехал вправо со скоростью в 1+x/2 раз меньше нашей за 2x минут до начала погони. И т.д. Рано или поздно наше предположение окажется соответствующим действительности, и мы его догоним.
1. Может, поэтому гонятся он будет очень долго, если не повезет сразу догнать. Но вопрос был о теоретической возможности, которую я и доказал.
2. Грубо говоря, а данном контексте, ε это такая величина, что ε = ε / 2; ε != 0; То бишь, сколь угодно малая величина, нет смысла ее делить. Ваше решение годно для нормальной константы, для ε так делать не нужно.
2. Грубо говоря, а данном контексте, ε это такая величина, что ε = ε / 2; ε != 0; То бишь, сколь угодно малая величина, нет смысла ее делить. Ваше решение годно для нормальной константы, для ε так делать не нужно.
Маленькая проблема: такого ε среди вещественных чисел не существует. А скорость автомобиля всё же должна быть вещественным числом:)
Странно, что для вас это проблема). Для меня нет). Это я грубо говоря, говорил. Ну просто константа, которая достаточно мала, чтобы гарантировано быть меньше разности скоростей. Не того уровня задача, чтобы протестовать против такого утверждения.
ИМХО, в этом один из основных пунктов этой, действительно несложной, задачи. Такой константы, по условию, нет.
И для меня всегда проблема, когда люди начинают использовать исчисление бесконечно малых нестрого. Очень уж легко получить таким образом неверные утверждения.
Хотите использовать бесконечно малые в точности как обычные числа — к вашим услугам нестандартный анализ, в котором, правда, есть свои заморочки. Иначе нужно учитывать аксиому Архимеда и аккуратно переходить к пределам.
Хотите использовать бесконечно малые в точности как обычные числа — к вашим услугам нестандартный анализ, в котором, правда, есть свои заморочки. Иначе нужно учитывать аксиому Архимеда и аккуратно переходить к пределам.
Хорошо, тогда берем за финальное решение то, что предложил petropavel.
Ради всего святого, дайте еще задачек!!! И, по возможности, посоветуйте сборник таких вот задачек.
По второй задаче, нужно выбрать внутренний квадрат (круг), перемещение по которому будет происходить быстрее чем собаки будут адаптироваться под положение волка. Перемещаясь по такому квадрату (кругу) волк вероятно сможет привести собак в положение, когда он сможет выйти убив одну из собак или никого не убивая.
1-я задачка не очень корректно сформулирована, но решается:
Коп должен ехать Х часов в одну сторону. потом развернуться, вернуться до тюрьмы и ехать в другую сторону. В каждой итерации нужно заезжать в N раз дальше чем в предыдущей итерации. Например — ехать 1 час на юг, вернуться, ехать 10 часов на север, вернуться, ехать 100 часов на юг, вернуться, и т.д. Чем больше N тем раньше догонит.
2-я задачка вообще примитив — у волка нет шансов. Проведем через волка две прямые, параллельные диагоналям (!!!) квадрата. Собаки должны в точках пересечения этих прямых со стенками квадрата. волку капец.
Формулки можете самостоятельно на досуге написать…
Коп должен ехать Х часов в одну сторону. потом развернуться, вернуться до тюрьмы и ехать в другую сторону. В каждой итерации нужно заезжать в N раз дальше чем в предыдущей итерации. Например — ехать 1 час на юг, вернуться, ехать 10 часов на север, вернуться, ехать 100 часов на юг, вернуться, и т.д. Чем больше N тем раньше догонит.
2-я задачка вообще примитив — у волка нет шансов. Проведем через волка две прямые, параллельные диагоналям (!!!) квадрата. Собаки должны в точках пересечения этих прямых со стенками квадрата. волку капец.
Формулки можете самостоятельно на досуге написать…
Легко доказать, что так коп преступника не догонит. Пусть у копа скорость V, а у преступника — U. Коп проезжает вначале V километров на юг за час, потом VN километров на север за N+2 часа, потом VN2 километров на юг за N2+2N+2 часов, и так далее. В общем, на каждом шаге он проезжает в какую-то сторону VNk километров за
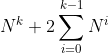
часов, в течение которых преступник едет в одну сторону с постоянной скоростью U. Чтобы коп догнал преступника, необходимо чтобы
)
или
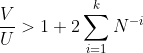
Поскольку коп не знает, насколько его машина быстрее, то N выбирается не зная V/U. И какое бы N коп не выбрал, всегда может оказаться, что V/U достаточно мало, чтобы нарушить это неравенство при любом k. И тогда коп никогда не догонит преступника.
На самом деле, конечно, догонит, доказательств достаточно выше в обсуждении. Но ему нужно будет ехать не «в N раз дальше чем в предыдущей итерации». Расстояние должно возрастать быстрее, чем по экспоненте. Об этом тоже, впрочем, выше уже упоминалось, но без формул.
часов, в течение которых преступник едет в одну сторону с постоянной скоростью U. Чтобы коп догнал преступника, необходимо чтобы
или
Поскольку коп не знает, насколько его машина быстрее, то N выбирается не зная V/U. И какое бы N коп не выбрал, всегда может оказаться, что V/U достаточно мало, чтобы нарушить это неравенство при любом k. И тогда коп никогда не догонит преступника.
На самом деле, конечно, догонит, доказательств достаточно выше в обсуждении. Но ему нужно будет ехать не «в N раз дальше чем в предыдущей итерации». Расстояние должно возрастать быстрее, чем по экспоненте. Об этом тоже, впрочем, выше уже упоминалось, но без формул.
Исходя из условия, у меня получилось, что у волка нет шансов.
Если бы собаки могли перемещаться только до соседнего угла, тогда можно было бы обмануть.
А так получается:
можно принять, что охранять его будут две собаки, к которым он начал движение из центра, а две остальные на подстраховке. Чем ближе он к «охранникам-собакам» тем, они ближе друг к другу при смещении в любую сторону по часовой или против собаки смещаются в этом же направлении, сохраняя необходимые расстояния.
или нужно математически описать?
Если бы собаки могли перемещаться только до соседнего угла, тогда можно было бы обмануть.
А так получается:
можно принять, что охранять его будут две собаки, к которым он начал движение из центра, а две остальные на подстраховке. Чем ближе он к «охранникам-собакам» тем, они ближе друг к другу при смещении в любую сторону по часовой или против собаки смещаются в этом же направлении, сохраняя необходимые расстояния.
или нужно математически описать?
Sign up to leave a comment.
Пара задачек с YAC 2012