Comments 65
Алгоритм можно сделать ещё более быстрым, если вместо двух проходов всё делать за один проход без использования промежуточного изображения. Особенно сильно разница будет заметна при параллельно-векторной реализации, когда производительность будет упираться в память.
Если на пальцах: пусть нам надо построить строку j с помощью билинейной интерполяции. Тогда для её построения нам достаточно только двух строк из исходного изображений (для бикубической — четыре). Сначала делается интерполяция по вертикали — это простая сумма двух строк из исходного изображения с определёнными коэффициентами. А сделать интерполяцию строки по горизонтали проблем нет.
Ну и сильно проще становится, когда коэффициент увеличения фиксированный, например 2 или 4.
пусть нам надо построить строку j с помощью билинейной интерполяции. Тогда для её построения нам достаточно только двух строк из исходного изображений
Это верно только при увеличении. Можно сделать частный случай.
Это верно только при увеличении
Это почему же?
А вообще, для уменьшения не стоит использовать использовать ни билинейную, ни бикубическую интерполяцию в чистом виде — алиасинг попрёт. Либо комбинировать с предварительной фильтрацией (размытием), либо строить адаптивное ядро.
Это почему же?
Не важно сколько именно, главное что нужно конечное количество строк. Смотрите например как я в своё время сделал для RawTherapee
Интерполяция с помощью линейных фильтров выглядит следующим образом:
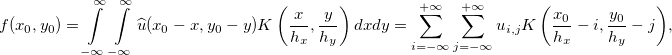
Т.е. строится непрерывное изображение, затем просто берутся значения в новых узлах.
При этом не имеет никакого значения — увеличивается ли картинка или уменьшается.
Вы сказали, что «для её построения нам достаточно только двух строк», что не так и ваша формула с суммой от -∞ до +∞ это подтверждает.
Видимо, я переборщил с матаном (из диссера выдрал). Вот более понятная формула:

Суть такова: есть дискретное изображение u, заданное в целочисленных узлах (i, j), и ядро интерполяции K(x, y) = K(x)K(y) — примеры ядер в Вашей предыдущей публикации есть. Далее делается свёртка дискретного изображения (сумма дельта-функций) с непрерывным ядром — получается непрерывное изображение u(x, y). Далее просто спокойно считаем значения там, где они нам нужны.
Так как в случае билинейной интерполяции K(x) равно 0 вне интервала (-1, 1), то в сумме будет использоваться не более двух точек с ненулевыми коэффициентами по каждой из координат. В случае бикубической — не более 4 точек.
А куда из вашей формулы делись hx и hy?
Я их приравнял единице. Это шаг сетки. ui, j = u(ihx, ihy).
Почему вы приравняли их 1?
K(x) и K(y) от целых чисел всегда равно нулю (см графики). По вашей последней формуле x,y и i,j — целые, поэтому K(x) и K(y) не равны нулю только в 0 и ваша последняя формула полностью эквивалентна u(x, y) = ui,j
(i, j) — целые, (x, y) — вещественные
А приравнял единице, чтобы считать проще было. Просто изначально задача была более общая: математическая модель построения пиксельного изображения на матрице камеры.
А приравнял единице, чтобы считать проще было.
Классно вы. Так вот, если вы их не просто выкинете, а сделаете сетку u(x, y) в масштабе конечного изображения, вы и получите метод сверток, в котором размер фильтра K зависит от масштаба и соответственно для уменьшения нужно будет больше, чем 2 строки и 2 ряда. Именно об этом методе и идет речь в статьях.
Ваше исходное утверждение «можно сделать быстрее, если делать за один проход» может оказаться верным, надо проверять. Но ваша фраза «нам достаточно только двух строк из исходного изображений» не верна.
Вот что бывает, когда «приравнял единице, чтобы считать проще было».
в котором размер фильтра K зависит от масштаба
В том-то и дело, что не зависит.
Было изображение ui, j, хотим увеличить/уменьшить в s раз и получить vi, j. Считаем: vi, j = u(i / s, j / s). Так как координаты (i / s, j / s) вещественные, интерполируем по формуле выше.
Вот чтиво — изучайте B. Generalized interpolation.
Я не очень понимаю, какую цель вы преследуете. Вы меня пытаетесь убедить, что у меня считается не так, как я думаю? Или что так как у меня, считать неправильно? Выше вы написали:
для уменьшения не стоит использовать использовать ни билинейную, ни бикубическую интерполяцию в чистом виде
Если вы считаете то, что вы описываете (приравнял единице) «чистым видом», то я её и не использую как раз. У меня как раз таки «адаптивное ядро», как вы советуете.
Я не очень понимаю, какую цель вы преследуете. Вы меня пытаетесь убедить, что у меня считается не так, как я думаю?
Нет, я просто пытаюсь убедить, что для построения одной строки результирующего изображения достаточно доступа к двум строкам исходного. Доказываю через формулу. И это будет работать и для увеличения, и для уменьшения, потому что интерполяция от этого не меняется.
Разве это не логично? Если мы хотим найти значение промежуточной точки с помощью билинейной интерполяции, нам нужно только 4 окрестные точки (квадрат 2х2), и ничего больше. Если с помощью бикубической, то 4х4.
пытаюсь убедить, что для построения одной строки результирующего изображения достаточно доступа к двум строкам исходного
Вы можете строить результирующее изображение, используя хоть одну строку исходного изображения, хоть ноль. Пожалуйста, кто вам запретит. Но результат будет вот такой. Для ваших целей это может быть приемлемо, для моих нет.
Если мы хотим найти значение промежуточной точки
Я не знаю, зачем вы это хотите. Дело ваше, опять же. В первой статье я описал, чего хочу я и почему.
У меня как раз таки «адаптивное ядро», как вы советуете.
Если вы под адаптивным ядром при уменьшении понимаете растяжение ядра сразу на много пикселей, т.е. при уменьшении в 10 раз шапочка линейного фильтра накрывает 21 пиксель, то да, такой способ вполне себе имеет право на жизнь.
Но такое уменьшение будет довольно далеко от реальных моделей, где в качестве функций рассеяния точки берётся функция Гаусса или прямоугольник.
Поэтому я бы советовал при уменьшении делать сначала фильтрацию Гаусса, затем применять неадаптивный фильтр.
Функцию Гаусса или прямогольник берут только в учебниках, чтобы считать было проще. Как показала история и исследования, для изображений подходит функция типа Ланцоша.
Все ядра для интерполяции — это вариации на тему фильтра низких частот. Идеальный ФНЧ — это sinc(x), но он требует бесконечно широкого окна. В реальных фильтрах же для удобства вычислений используют разные его приближения, Ланцош из которых является одним из наиболее точных
В реальных фильтрах же для удобства вычислений используют разные его приближения, Ланцош из которых является одним из наиболее точных
Я собственно это и имел ввиду.
Идеальный ФНЧ — это sinc(x), но он требует бесконечно широкого окна
А ещё он требует выполнения условий теоремы Котельникова. Но на практике изображений с ограниченной частотой, за редким исключением, просто не существует. Поэтому если увеличивать изображение с помощью sinc, то полезет рингинг (эффект Гиббса).
На деле, какой фильтр не выбери, на выходе будет комбинация между алиасингом, размытием и рингингом. Если бороться с одним эффектом, вылезеть другой, оптимального фильтра нет. Ланцош — это просто хороший компромисс между этими эффектами.
Возьмите любую современную научную публикацию по суперразрешению (желательно многокадровому). В модели понижения разрешения используют в подавляющем большинстве случаев Гаусса, совсем редко — прямоугольный фильтр.
Есть научно обоснованная математическая модель, а есть простые фильтры, которые применяют, когда математическую модель по какой-то причине применить нельзя. Противоречий здесь нет.
Вы мешаете в кучу две совершенно разные вещи.
Как раз наоборот: я их не мешаю, а разделяю. Мешают их те, кто пытается две вещи делать одновременно: интерполяцию одновременно с подавлением алиасинга.
такой способ вполне себе имеет право на жизнь
Спасибо большое. За сим предлагаю закончить.
При уменьшении изображения в N раз частота Найквиста уменьшается тоже в N раз.
Дабы избежать алиасинга Вам нужно в качестве ядра взять фильтр низких частот который отрежет частоты выше частоты Найквиста. Очевидно что для разных N и разных частот Найквиста этот фильтр будет разным. И простейший способ получить такой фильтр — это взять ФНЧ для частоты Найквиста в исходном изображении, а затем растянуть его в пространственном домене в N раз (это сожмет его в частотном в N раз же, что нам для соответствия новой частоте Найквиста и требуется). Поэтому при сжатии в 2 раза ядро «правильной билинейной» интерполяции будет уже задано на [-2,2] а не [-1,1]. При работе же с билинейкой [-1,1] в таком сценарии Вы получите замечательный алиасинг т.к. частоты между «старой» и «новой» частотами Найквиста не будут подавлены. Вот при апсемплинге такой проблемы нет и там ядро всегда будет определяться частотой Найквиста в исходном сигнале, там ядро действительно получается константным.
Функции рассеяния, кстати, тут вообще не при чем. Вы ее применили один раз, при оцифровке исходного изображения и все, дальше можете забыть: она навсегда стала частью оцифрованного сигнала. Исключением является только тот случай когда Вы последующей обработкой пытаетесь ее компенсировать.
Спасибо вам большое! Как вы видите, меня больше интересует прикладная сторона и моих знаний недостаточно чтобы объяснить почему так правильно, а так неправильно. Но теперь у меня будет место, куда я смогу ссылаться.
У вас просто однобокий взгляд на проблему. Судя по всему, вы занимаетесь чисто прикладными задачами, скорее всего — компьютерной графикой, визуализацией, либо не очень сложной обработкой.
моих знаний недостаточно чтобы объяснить почему так правильно, а так неправильно
Эффект Даннинга — Крюгера имеет место быть, причём в отношении нас обоих.
Оба варианта правильные, просто применяются в совершенно различных задачах.
Дабы избежать алиасинга Вам нужно в качестве ядра взять фильтр низких частот который отрежет частоты выше частоты Найквиста
Да, я это прекрасно знаю. Но я предпочитаю разделять эти две операции. При уменьшении я сначала делаю фильтрацию, затем decimation по моей формуле. Так получается быстрее, чем при объединении этих операций, и вот почему: при интерполяции коэффициенты у каждого пикселя получаются свои (особенно если уменьшение идёт в нецелое число раз), поэтому пересчитывать эти коэффициенты желательно по-минимуму.
ФНЧ эффективно применяется дважды
Зависит от коэффициента уменьшения:
- если коэффициент целый, то второй проход не применяется, просто выкидываем каждый N-й пиксель;
- если коэффициент большой (4 раза и больше) — искажения, вносимые при интерполяции, не оказывают хоть сколько-нибудь заметного эффекта;
- если коэффициент маленький (от 1 до 2) — вот это уже самый сложный случай, здесь действительно приходится обходиться одним фильтром, только я предпочитаю бикубик, а не Ланцоша из-за скорости.
Ну а количество проходов по памяти, естественно, должно быть по-минимуму. В идеале, всё должно делаться за один проход, просто реализация будет более трудоёмкой.
Функции рассеяния, кстати, тут вообще не при чем. Вы ее применили один раз, при оцифровке исходного изображения и все, дальше можете забыть: она навсегда стала частью оцифрованного сигнала. Исключением является только тот случай когда Вы последующей обработкой пытаетесь ее компенсировать.
Ну и отдельно про функцию рассеяния точки: иногда она используется.
Задачу уменьшения изображения можно сформулировать так: по изображению U, полученному с камеры с определённым разрешением и определённой функцией рассеяния точки (PSF), построить изображение V, как если бы оно было получено с такой же камеры, но в S раз меньшим разрешением и пропорционально растянутой PSF.
Соответственно, здесь низкочастотный фильтр, применяемый для уменьшения изображения, напрямую связан с PSF камеры. А на PSF камеры влияет дефокус/апертура и собственно сенсор. Если мы хотим получить изображение, максимальное приближенное к реальному, PSF придётся использовать. А если просто уменьшить картинку — да что угодно.
SR-методы опираются на универсальную модель формирования цифрового изображения «свернули непрерывное изображение с PSF, сделали выборку по дискретной сетке (дискретизацию)». И все они пытаются так или иначе восстановить непрерывное изображение, хотя и формируют лишь его представление с другой PSF и/или частотой дискретизации. Оба этапа (свертка и дискретизация) вносят определенные искажения. Свертку можно убрать deconvolution и более сложными image-aware аналогами, для этого (если PSF >> размера пикселя) в принципе достаточно даже одного изображения. Дискретизация вносит алиасинг (мешающий деконволюции), поэтому выше разрешения исходного изображения (не прибегая к уловкам с «угадыванием» изображения) так не подняться, но если у нас есть набор картинок, то алиасинг можно подавить и получить новую, более мелкую дискретизацию (картинку с субпиксельным разрешением)
Так вот: гаусс и вообще PSF и дискретизация — разные вещи дающие разные эффекты с которыми борются по разному. А такой задачи ресайза как Вы описываете и в помине никто не ставит.
Задача уменьшения изображения — это просто downsampling исходного сигнала, полностью самостоятельная задача не имеющая никакого отношения к PSF(т.к. downsamplится сигнал уже свернутый с PSF).
Если коэффициент уменьшения небольшой (1-1.5) или картинка просто аффинно деформируется, то пиксельный PSF будет играть весьма большую роль, т.к. его частотные характеристики будут сильно искажать характеристики интерполяционного фильтра.
А такой задачи ресайза как Вы описываете и в помине никто не ставит.
Такая задача существует, просто не используется в чисто прикладных задачах. Видимо, для расширения кругозора местных обитателей и разрешения холивара, которого на самом деле нет, я в ближайшее время напишу статью о том, какие вообще существуют подходы для работы с изображениями и где они используются.
Наилучшее качество при уменьшении достигается, кстати, не Ланцошом, а специальными методами обработки, которые оперируют с изображением не как с абстрактным сигналом, а как с изображением, на котором есть определённые информация, специфичная именно для изображений, о качестве которой стоит задуматься, например:
Content aware image downsampling.
По остальному — Вы в какую-то специфичную задачу закапываетесь. Там есть разные подходы конечно, но я могу точно сказать что на основании специфики этой Вашей задачи Вы много фигни разной выше в комментариях написали о другой задаче (ресемплинге изображений).
Content-aware методы это отдельный разговор, да. Я в комментариях это вроде везде пытался оговорить отдельно.
import cv2
extra_smoothing_factor = 0.3 # more = less aliasing, but more blur
im = cv2.imread(r"d:\pixar.jpg")
downsampling_factor = im.shape[0] / 512
im = cv2.GaussianBlur(im, (0,0), sigmaX=downsampling_factor*extra_smoothing_factor)
im = cv2.resize(im, (512, 214), interpolation=cv2.INTER_LINEAR)
cv2.imwrite(r"d:\pixar.cv2.jpg", im)
Это вполне жизнеспособный подход и он должен быть довольно быстрым, хотя и менее качественным. Заменой гауссова размытия на более качественный low-pass filter kernel можно добиться лучшего результата, но из коробки в cv2 я сходу альтернатив не нашёл
И encyclopedist предложил отличную оптимизацию для общего ресайза свертками, подобный подход даст хорошую прибавку к скорости
DistortNeo предлагает примерно такой вариант ресайза
Конечно же нет. DistortNeo предлагал «всё делать за один проход без использования промежуточного изображения». У вас тут добавляется еще два прохода для блюра. Но давайте все равно посмотрим на ваше предложение.
Это вполне жизнеспособный подход и он должен быть довольно быстрым
Он по определению не может быть более быстрым. Начну с того, что непонятно как вы задали extra_smoothing_factor = 0.3. При этом значении результат получается ну очень aliased. Так-то и в свертках можно сильно уменьшить радиус фильтра и получить то же самое по качеству и выигрышу в производительности. Так что давайте возьмем значение, когда результат более-менее похоже на бикубик.
extra_smoothing_factor = 0.8
Смотрите сами, GaussianBlur это тоже свертка. Радиус её равен 0.8 × W / w × ≈2.5, где ≈2.5 — коэффициент, на который opencv домножает сигму, чтобы определить границы GaussianBlur. Мне не известно точное значение, известно что для качественного блюра оно должно быть от 2 до 3.
Т.е. в вашем варианте происходит W×H сверток с радиусом W / w × 2. Если делать как я, то понадобится w×h сверток с радиусом W / w × 2. Ну очевидно же, что при уменьшении W×H >> w×h. Что и подтверждается практикой:
In [38]: im = Image.open('../pixar.jpg')
...: im.load()
...: %time im.resize((512, 214), Image.BICUBIC)
...:
Wall time: 34.1 ms
In [39]: extra_smoothing_factor = .8
...: im = cv2.imread(r"../pixar.jpg")
...: %time im = cv2.GaussianBlur(im, (0,0), sigmaX=downsampling_factor*extra_smoothing_factor)
...: %time im = cv2.resize(im, (512, 214), interpolation=cv2.INTER_LINEAR)
...: cv2.imwrite(r"../pixar.cv2.03.png", im)
...:
Wall time: 582 ms
Wall time: 1.39 msОптимальный уровень размытия Гауссом: extra_smoothing_factor = 0.3 * sqrt(s * s - 1), где s — коэффициент уменьшения. Уменьшаем в 2 раза — значит, надо размывать с 0.7 — 0.75. Уменьшаем в 8 раз — будет сигма 2.38 и размер фильтра 2 * 8 + 1 = 17 пикселей. Не забываем также, что при больших коэффициентах можно использовать быструю аппроксимацию фильтра Гаусса. А если он хреново реализован в OpenCV — что ж, страдать теперь? Берём C++ и реализовываем.
При большом коэффиценте s никуда не деться — будет 2 прохода, и самый затратный — это антиалиасинг. Но отличие вот в чём: в вашем случае коэффициенты фильтра будут разные для каждого пикселя. В моём же случае это полноценная свёртка — т.е. код получается легко векторизуемым. Впрочем да, ваш код тоже можно эффективно векторизовать, если предварительно посчитанные коэффициенты размещать в памяти немного по-другому.
Оптимальный уровень размытия
Оптимальный для чего? Я же говорю, что результат получается очень aliased.
Оптимальный для чего? Я же говорю, что результат получается очень aliased.
Оптимальный для уменьшения фотографических изображений (не абстрактной графики).
Вы, видимо, даже не попробовали написанное. Ну ладно, я помогу.
Вот исходник и результат уменьшения в 2, 4 и 8 раз, описанный мной.




Понял, в чем проблема. В opencv координаты перевернуты и im.shape[0] — это высота изображения. Картинка сильно горизонтальная, поэтому downsampling_factor из начального комментария 0serg был сильно занижен. 0.3 действительно нормальное значение.
Тем не менее sigmaX получается такая же, производительностью я правильно намерил. Так что все равно получается в 15 раз медленнее. В OpenCV блюр не аппроксимация, но реализован очень хорошо и при сигме 3.9 работает со скоростью аппроксимации, а то и быстрее.
Так что все равно получается в 15 раз медленнее.
… при использовании OpenCV
Теперь смотрим ваши результаты:
im.resize((512, 214), Image.BICUBIC) -> Wall time: 34.1 ms
cv2.resize(im, (512, 214), interpolation=cv2.INTER_LINEAR) -> Wall time: 1.39 ms
Если делать низкочастотную фильтрацию быстрее, чем за 30 мс, то получим явное преимущество в скорости работы. И это преимущество раскрывается при больших коэффициентах уменьшения (8 и выше). Ну а то, что фильтр Гаусса в OpenCV такой медленный — это камень в огород OpenCV,
Конечно же нет. DistortNeo предлагал «всё делать за один проход без использования промежуточного изображения». У вас тут добавляется еще два прохода для блюра. Но давайте все равно посмотрим на ваше предложение.
Он свои мысли плохо излагает, но идея у него была именно эта.
Он по определению не может быть более быстрым. Начну с того, что непонятно как вы задали extra_smoothing_factor = 0.3. При этом значении результат получается ну очень aliased.
Чисто эмпирически, для Гаусса нет хорошей четкой границы частотного отсечения. По хорошему там вообще нормальный ФНЧ нужен, просто «из коробки» ничего лучше Гаусса OpenCV вроде не предлагает
Т.е. в вашем варианте происходит W×H сверток с радиусом W / w × 2. Если делать как я, то понадобится w×h сверток с радиусом W / w × 2. Ну очевидно же, что при уменьшении W×H >> w×h. Что и подтверждается практикой:
В этом плане да, согласен. Вообще говоря лишние пиксели которые не нужны потом в расчетах там по хорошему бы просто не нужно считать, но с точки зрения имплементации это серьезная проблема в которую подход DistortNeo так или иначе упрется.
Если в исходном изображении будет шахматная сетка из пикселей со значениями (0,0,0) и (255,255,255), то каким будет результат уменьшения в два раза? Серый однородный фон? Серый цвет будет (127,127,127)? Или (128,128,128)? Или же (188,188,188)?
Итоговое изображение не будет соответствовать исходному. Особенно весело будет, есть ресайзнутое таким образом изображение будет ресайзнуто ещё раз или несколько.
Как минимум, надо предупреждать пользователей об этом, не все ж в курсе нелинейности sRGB пространства и подобных фокусов.
Игнор гаммы обычно не приводит к негативным последствиям, зато позволяет не тратить ресурсы на дополнительные преобразования гаммы. Глядя на изображение, вы визуально не поймёте, было ли оно уменьшено с учётом гаммы, или нет. Только на специальных паттернах можно заподозрить неладное.
Прямое преобразование (из sRGB в линейное) — это прямой lookup по таблице в 256 элементов — не сказать что сильно большая потеря в скорости. Обратное преобразование уже сложнее, но все равно это максимум бинарный поиск по этой же таблице, без всяких умножений и логарифмов.
Прямое преобразование (из sRGB в линейное) — это прямой lookup по таблице в 256 элементов — не сказать что сильно большая потеря в скорости. Обратное преобразование уже сложнее, но все равно это максимум бинарный поиск по этой же таблице, без всяких умножений и логарифмов.
Есть маленький нюанс: векторизовать такой код уже не получится. А значит, можно просесть в скорости на порядок только на этом.
При использовании векторных операций, скорее всего, быстрее выйдет честно (или приближённо — небольшая ошибка роли не играет) возводить число в степень.
будете видеть равномерный серый цветЯ не против серого цвета, я против того, что его значение вычисляется некорректно.
Но всё равно очень круто :)
Часто компилятор в Линуксе — часть операционной системы и обновляется только с ней. Релизы Убунты LTS, например выходят раз в 2 года и актуальны года 4.
Как я сделал самый быстрый ресайз изображений. Часть 1, общие оптимизации