Часть 2. Very Heavy Fuel
Предыдущая часть 1
Перед вами — Международная Космическая Станция. Массой в 420 тонн и стоимостью[20] в $150 миллиардов:

Её кинетическая энергия, старое доброе E = mv2/2, составляет 1.3*1013 джоулей. Добавив потенциальную энергию на высоте 400 километров, получим 1.4*1013 Дж.
Сколько бензина надо сжечь, чтобы получить эту энергию? Оказывается, не так уж и много. 350 тонн всего. Это примерно[200] однодневный энергетический бюджет Улан-Удэ.
Как же так получается, что далеко не самый богатый город мира за один-единственный день распоряжается энергией, достаточной для разгона МКС до орбитальной скорости, однако же станция у нас на весь мир одна, и стоит неприлично бешеных денег?
Ответ
Носитель, как минимум, обязан включать в себя:
- Полезную нагрузку. Иначе зачем он вообще нужен?
- Хотя бы один двигатель.
- Корпус, всё это соединяющий.
- И, разумеется, топливо. Как рабочее тело и, в большинстве случаев, как источник энергии.
И вот в последнем-то пункте и коренится проблема. Чтобы поднять и утащить некий минимум топлива, нужно… правильно, дополнительное топливо! На подъём которого нужно тоже топливо! И эта накрутка продолжается долго. Она, конечно, сходится, иначе бы мы вообще никуда не летали. Но по результатам сходимости современная ракета, даже многоступенчатая, даже качественно спроектированная и выполненная, по массе состоит преимущественно из этого самого топлива.
Ну вот хрестоматийный пример, Saturn V — не самая новая, но одна из самых эффективных ракет в истории[30]:

[Original image from NASA History [40]]
Стартовая масса — 2970 тонн. Из них где-то 2670 — топливо. Из которых 2160 выгорают меньше чем за три минуты всей лунной экспедиции. При том, что кинетическая энергия полезной нагрузки на орбите «стоит» всего-то тонн 100 горючего.
Получается, главная трудность выхода на орбиту — это не недостаток энергии. Её землянам с избытком хватает на кинетическую энергию не то что станций, а хоть бы и круизных пароходов на орбите. Проблема в другом: наше топливо слишком тяжелое. Слишком много его надо в килограммах, чтобы собрать требуемое на полёт количество энергии. Отчего большая часть топлива, залитого в ракету, уходит на перевозку топлива же. Собственно, формула Циолковского, увязывающая стартовую M и финишную массу ракеты m с набранной скоростью V и скоростью истечения выхлопа двигателя u, говорит нам о том же:
M/m = eV/u [2]
На первый взгляд не совсем очевидно, при чём тут содержание энергии на килограмм? Но всё просто. Оно «сидит» в u, в скорости истечения. Для химического горючего она ограничена величиной (и в первом приближении равна ей) u = √(2q), где q — удельная теплота сгорания. Которая и есть содержание энергии на килограмм. И когда это q «не дотягивает», отношение масс на старте и финише оказывается экспоненциально громадным:
M/m = eV/√(2q) [3]
Или
V = Ln(M/m)*√(2q) [3a]
Несколько замечаний, для зануд и для ясности
1. Да, есть более точные выражения для скорости истечения, чем u = √(2q). Когда я сдавал по ним зачёт, Горбачёв «сдавал» СССР. Но эти формулы сложноваты, распугивают читателей, и учитывают эффекты, здесь неважные. u = √(2q), хоть и завышает ответ на 10-30%, адекватно описывает интересующую нас зависимость. И да, есть такое понятие, как удельный импульс, но в данной конкретной статье скоростью истечения пользоваться удобнее.
2. В принципе, ничто не запрещает даже химической ракете получить скорость истечения u выше, чем √(2q). Как? Ну, скажем, сжигать топливо не в сопле, а в генераторе, вырабатывая электрическую энергию. Затем этой энергией разгонять долю x выхлопа (0 < x ≤ 1) до очень высоких скоростей. Допустим, плазменным электрическим реактивным двигателем[230]. А остатки выхлопа тупо сбрасывать с нулевой скоростью. Для простоты положим, что все преобразования происходят без потерь энергии, со 100%-й эффективностью. Разгонится ли такая ракета до большей скорости V при фиксированном отношении масс M/m (т.е., будет ли она эффективней)?
Ответ отрицательный. Легко решить уравнения, описывающие движение такой ракеты, и получить:
V = Ln(M/m)*√(2qx)
Т.е. её конечная скорость составит лишь √x от набранной «обычной» ракетой с непосредственным сжиганием топлива (ср. с [3a]). И эта скорость всё равно жёстко завязана на величину q.
3. Что если ракета работает не на топливе, а на батарейке? Ну вот пусть на борту есть отдельно рабочее тело массы mf и отдельно — батарейка с запасом энергии E и массой mb.
Первое, что здесь надо понять — это что батарейка должна состоять из множества небольших «модулей», сбрасываемых по мере отработки. Ибо в противном случае мы будем тащить с собой «мёртвый» груз пустых батарей. Но если так, то концептуально это ничем не отличается от обычного топлива на борту с полным запасом энергии E и массой mf + mb. И если q = E/(mf + mb) такой системы ниже, чем у обычной химической ракеты, то и улетит она не лучше.
5. А как же электрические ракетные двигатели[225]? Они ведь дают скорости истечения в десятки и сотни километров в секунду, и на них совершались успешные межпланетные манёвры при весьма скромных отношениях M/m. Как так? Дело в том, что ЭРД — незамкнутые системы. Рабочее тело (ртуть, ксенон и т.п.) они везут с собой. А вот энергию — нет. Энергия поступает с солнечных батарей. Если бы вместо этого они несли с собой обычные батарейки с содержанием энергии на массу q, то и эффективность у них была бы не выше, по формуле [3a].
2. В принципе, ничто не запрещает даже химической ракете получить скорость истечения u выше, чем √(2q). Как? Ну, скажем, сжигать топливо не в сопле, а в генераторе, вырабатывая электрическую энергию. Затем этой энергией разгонять долю x выхлопа (0 < x ≤ 1) до очень высоких скоростей. Допустим, плазменным электрическим реактивным двигателем[230]. А остатки выхлопа тупо сбрасывать с нулевой скоростью. Для простоты положим, что все преобразования происходят без потерь энергии, со 100%-й эффективностью. Разгонится ли такая ракета до большей скорости V при фиксированном отношении масс M/m (т.е., будет ли она эффективней)?
Ответ отрицательный. Легко решить уравнения, описывающие движение такой ракеты, и получить:
V = Ln(M/m)*√(2qx)
Т.е. её конечная скорость составит лишь √x от набранной «обычной» ракетой с непосредственным сжиганием топлива (ср. с [3a]). И эта скорость всё равно жёстко завязана на величину q.
3. Что если ракета работает не на топливе, а на батарейке? Ну вот пусть на борту есть отдельно рабочее тело массы mf и отдельно — батарейка с запасом энергии E и массой mb.
Первое, что здесь надо понять — это что батарейка должна состоять из множества небольших «модулей», сбрасываемых по мере отработки. Ибо в противном случае мы будем тащить с собой «мёртвый» груз пустых батарей. Но если так, то концептуально это ничем не отличается от обычного топлива на борту с полным запасом энергии E и массой mf + mb. И если q = E/(mf + mb) такой системы ниже, чем у обычной химической ракеты, то и улетит она не лучше.
5. А как же электрические ракетные двигатели[225]? Они ведь дают скорости истечения в десятки и сотни километров в секунду, и на них совершались успешные межпланетные манёвры при весьма скромных отношениях M/m. Как так? Дело в том, что ЭРД — незамкнутые системы. Рабочее тело (ртуть, ксенон и т.п.) они везут с собой. А вот энергию — нет. Энергия поступает с солнечных батарей. Если бы вместо этого они несли с собой обычные батарейки с содержанием энергии на массу q, то и эффективность у них была бы не выше, по формуле [3a].
Статья написана для сайта https://habr.com. При копировании просьба ссылаться на исходник. Автор статьи Евгений Бобух.
Итак, ракеты дорогие потому, что их крайне лёгкая «сухая» конструкция вынуждена выдерживать крайне тяжёлую нагрузку, в основном топлива (да ещё и быстро «прокачивать» её через ТНА). А нагрузка велика потому, что наше топливо слишком тяжело. Очень уж мало в нём помещается джоулей на килограмм.
Давайте теперь поймём причины этого ограничения.
Для чего взглянём поближе на реакцию горения водорода во фторе, как одну из самых простых. В ней пары «водород-водород» и «фтор-фтор» обмениваются партнёрами, создавая две пары «водород-фтор»:
H2 + F2 = 2HF
Откуда берётся выделяющаяся энергия?
У молекулы водорода есть два атома. У атомов есть электроны. Они «размазаны» вокруг атома в виде эдакого облака, и связаны с ядром главным образом электростатическим притяжением. Электроны бывают внешние, валентные, и (кроме водорода) внутренние, в химических реакциях не участвующие. После реакции водород со фтором меняются местами. Электрические облака валентных электронов перераспределяются и слегка меняют форму. Как-то примерно так:

[Image credit [295]]
Потенциальная энергия связи электронов с атомами в новых облаках оказывается другой. В данном случае (эта энергия отрицательна) она теперь меньше, чем у H2 и F2 по отдельности. Куда пошла разница? В кинетическую энергию молекулы, колебания её атомов, электромагнитное излучение. Всё это в итоге превратилось в тепло. Которое расширило газ и дало тягу.
И здесь критически важен вот какой момент. В химических реакциях участвуют лишь внешние, валентные электроны. Распределение плотности прочих электронов (равно как и напряжённость электрического поля «в глубине» атома) остаются практически неизменными. В химических реакциях атомы взаимодействуют друг с другом как бы через «посредников», какими выступают валентные электроны:

Теперь, внимание, вопрос: какова предельно возможная энергия, которая может выделиться при подобной «перестановке»? Очевидно, она не может превышать суммы энергий связи внешних электронов с атомами (в конечном и начальном продукте). Но эти энергии связи нам хорошо известны[285]. В расчёте на один атом они составляют 1.5 — 25 электронвольт (эВ) и выражаются в долях постоянной Ридберга — величины фундаментальной, конструируемой из базовых констант нашей Вселенной:
Ry (в Гауссовой системе) = mee4/2ħ2 = 13.6 эВ [300]
При этом и 25, и 13.6 эВ — недостижимы. Ибо в типичных реакциях высвобождается далеко не вся энергия связи, а только её разница между двумя конфигурациями, и поэтому практический потолок энерговыделения химии составляет 3-4 эВ на атом. В пересчёте на типичный килограмм горючего + окислителя это эквивалентно 20-30 МДж выделившейся энергии. Вот этой величиной и задаётся теоретическая максимальная скорость истечения газа химического реактивного двигателя с прямым сгоранием u = √(2q) = √(2*2.5*107) ≈ 7000 м/с. Недостижимая, конечно, ибо не учитывает потерь на внутренние степени свободы молекул, диссоциацию, излучение, ненаправленное тепловое движение и т.д.
Может показаться, что табличные теплоты сгорания[240] (скажем, 120 МДж/кг для водорода) выписанной выше цифре противоречат. Но дело в том, что эти теплоты обычно указываются на килограмм горючего, без учёта потребного для его сгорания окислителя. Ракета же везёт с собой оба компонента, и если пересчитать выделяющуюся энергию на килограмм смеси (при сбалансированном сгорании), то вырисовывается совсем другая картина[240][250][260]:
| Топливо + окислитель | Реакция | Теплота сгорания на кг. топлива, МДж/кг | На 1 кг топлива нужно окислителя, кг. | Теплота сгорания смеси, МДж/кг | Выход на атом смеси, эВ |
| Водород + кислород | 2H2 + O2 = 2H2O | 120 | 8 | 13.3 | 0.83 |
| Керосин + кислород | 2C12H26 + 37O2 = 24CO2 + 26H2O | 43 | 3.5 | 9.6 | 1.02 |
| Уголь + кислород | C + O2 = CO2 | 33 | 2.7 | 9.0 | 1.38 |
| Литий + кислород | 4Li + O2 = 2Li2O | 43.5 | 1.2 | 20.2 | 2.10 |
| Бор + кислород | 2B + 1.5O2 = B2O3 | 57.2 | 2.2 | 17.8 | 2.58 |
| Магний + кислород | 2Mg + O2 = 2MgO | 25.1 | 0.7 | 15.1 | 3.18 |
| Бериллий + кислород | 2Be + O2 = 2BeO | 66.6 | 1.8 | 24.0 | 3.12 |
| Литий + фтор | 2Li + F2 = 2LiF | 88.8 | 2.7 | 23.7 | 3.21 |
| Бериллий + фтор | Be + F2 = BeF2 | 114 | 4.2 | 21.9 | 3.57 |
| Дицианоацетилен + озон | C4N2 + (4/3)O3 = 4CO + N2 | 16.2 | 0.8 | 8.8 | 1.28 |
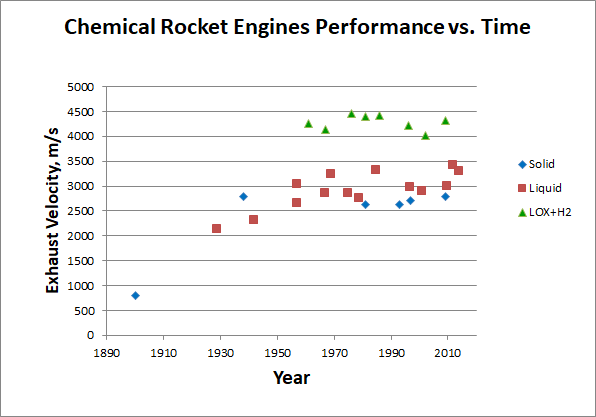
Как видим, даже самые энергоёмкие, пусть и непригодные для практического использования, виды топлива дают лишь 24 МДж/кг тепла при сгорании. И мы в этот предел упёрлись едва ли не с начала космонавтики, что показывает график скорости истечения химических двигателей в зависимости от года их создания:

[Ранние двигатели по данным [310], [320], [330], поздние — Википедия поштучно. Сборка данных здесь]
Похоже, потенциал химического топлива давно уже выработан. Не начать ли хранить энергию в другом виде?
Продолжение.
Ссылки и литература
[20] Международная Космическая Станция (включая стоимость): https://en.wikipedia.org/wiki/International_Space_Station
[30] Saturn V: https://en.wikipedia.org/wiki/Saturn_V
[40] NASA History: https://history.nasa.gov/SP-4206/p405.htm
[200] Улан-Удэ, статистика автомобилей: https://www.baikal-media.ru/news/transport/292121/
[225] Электрические двигатели в целом: https://en.wikipedia.org/wiki/Electrically_powered_spacecraft_propulsion
[230] Про плазменные электрические реактивные двигатели: https://en.wikipedia.org/wiki/Plasma_propulsion_engine
[240] Теплоты сгорания в воздухе: https://en.wikipedia.org/wiki/Heat_of_combustion#Heat_of_combustion_tables
[250] Ещё теплоты сгорания: https://books.google.com/books?id=9XbhDAAAQBAJ&pg=PA237&lpg=PA237&dq=heat+of+combustion+lithium+boron&source=bl&ots=9nLrWWUUwd&sig=OhqjfFkKUAxT1tJ1uL652WCXikQ&hl=en&sa=X&ved=2ahUKEwj23I7b_ZjfAhU8HjQIHbsEDEsQ6AEwDHoECAkQAQ#v=onepage&q=heat%20of%20combustion%20lithium%20boron&f=false
[260] Теплота сгорания бора во фторе: https://pdfs.semanticscholar.org/2cc8/9b76358223ee2dbdf83bb028f901048023be.pdf
[285] Энергии ионизации атомов: https://en.wikipedia.org/wiki/Ionization_energy
[295] Иллюстрация электронных облаков фтороводорода: https://slideplayer.com/slide/12471943/
[300] Постоянная Ридберга: https://en.wikipedia.org/wiki/Rydberg_constant
[310] Параметры ранних пороховых двигателей: https://www.thespacerace.com/forum/index.php?topic=2860.0
[320] Параметры ракетных моделей Годдарда: https://en.wikipedia.org/wiki/Robert_H._Goddard#Early_rocketry_research
[330] Параметры двигателя реактивного снаряда М-13 от «Катюши», вычислимы из данных в таблице 1 в http://epizodyspace.ru/bibl/iz-istorii/poroh.html
[30] Saturn V: https://en.wikipedia.org/wiki/Saturn_V
[40] NASA History: https://history.nasa.gov/SP-4206/p405.htm
[200] Улан-Удэ, статистика автомобилей: https://www.baikal-media.ru/news/transport/292121/
[225] Электрические двигатели в целом: https://en.wikipedia.org/wiki/Electrically_powered_spacecraft_propulsion
[230] Про плазменные электрические реактивные двигатели: https://en.wikipedia.org/wiki/Plasma_propulsion_engine
[240] Теплоты сгорания в воздухе: https://en.wikipedia.org/wiki/Heat_of_combustion#Heat_of_combustion_tables
[250] Ещё теплоты сгорания: https://books.google.com/books?id=9XbhDAAAQBAJ&pg=PA237&lpg=PA237&dq=heat+of+combustion+lithium+boron&source=bl&ots=9nLrWWUUwd&sig=OhqjfFkKUAxT1tJ1uL652WCXikQ&hl=en&sa=X&ved=2ahUKEwj23I7b_ZjfAhU8HjQIHbsEDEsQ6AEwDHoECAkQAQ#v=onepage&q=heat%20of%20combustion%20lithium%20boron&f=false
[260] Теплота сгорания бора во фторе: https://pdfs.semanticscholar.org/2cc8/9b76358223ee2dbdf83bb028f901048023be.pdf
[285] Энергии ионизации атомов: https://en.wikipedia.org/wiki/Ionization_energy
[295] Иллюстрация электронных облаков фтороводорода: https://slideplayer.com/slide/12471943/
[300] Постоянная Ридберга: https://en.wikipedia.org/wiki/Rydberg_constant
[310] Параметры ранних пороховых двигателей: https://www.thespacerace.com/forum/index.php?topic=2860.0
[320] Параметры ракетных моделей Годдарда: https://en.wikipedia.org/wiki/Robert_H._Goddard#Early_rocketry_research
[330] Параметры двигателя реактивного снаряда М-13 от «Катюши», вычислимы из данных в таблице 1 в http://epizodyspace.ru/bibl/iz-istorii/poroh.html