Comments 37
То, что ссылки в таблицах представлены полным URL и при этом не кликабельны — вызывает несколько меньшее количество удовольствия.
спасибо большое, все таки статистика дело наглядное.
Интересно не пользователи с максимальным рейтингом/подпиской, а пользователи с максимальным приростом и убытком рейтинга за год.
А вот мне было бы интересно увидеть, сколько постов написаны, так сказать, "от чистого сердца", то бишь без тега "Блог компании X"
Было бы неплохо провести подобное исследование с некоторыми оговорками:
Чтоб посмотреть не столько крутость показателей, сколько то благодарю чему удаются прорваться новичкам.
- Брать только хабраюзеров, выкинув блоги компаний
- При этом провести выборку по юзерам пришедшим на хабр, за последний год — два
Чтоб посмотреть не столько крутость показателей, сколько то благодарю чему удаются прорваться новичкам.
Около 12,5% было помечено тегом «Перевод», 10% с пометкой «Tutorial» и 4% с «recovery mode». Около 76% постов не имело таких отметок, при этом некоторые записи обозначены двумя и более тегами
Всего 102,5% постов?
Спасибо за отличный пост!
В 2015-м году написал пост под названием "Детальный анализ Хабрахабра с помощью языка Wolfram Language (Mathematica)", в котором были проанализированы все доступные на тот момент посты (за исключением тех, у которых отрицательная карма (не учел, так как не попали в тот момент в поле зрения, на что указали в комментариях) и мегапостов (не помню, были ли они тогда, если честно)). Рад, что результаты перекликаются с вашим исследованием.

В 2015-м году написал пост под названием "Детальный анализ Хабрахабра с помощью языка Wolfram Language (Mathematica)", в котором были проанализированы все доступные на тот момент посты (за исключением тех, у которых отрицательная карма (не учел, так как не попали в тот момент в поле зрения, на что указали в комментариях) и мегапостов (не помню, были ли они тогда, если честно)). Рад, что результаты перекликаются с вашим исследованием.

Спасибо! У вас тоже отличный анализ проведен. Возник вопрос, проводилась ли чистка данных на «выбросы из распределения» перед анализом?
Там, где я работал со статистикой и теорией вероятности, использовал SKD (Kernel density estimation), что устраняет выбросы, однако тесты вроде хи-квадрат не проводились, так как вообще говоря практически все они работают исходя из гипотезы о нормальности распределения, а тут видно, что они не все нормальные, а некоторые являются скорее смесью распределений.
Эти вопросы крайне интересные. Возможно у меня будет когда-то время продолжить начатый анализ.
Эти вопросы крайне интересные. Возможно у меня будет когда-то время продолжить начатый анализ.
UFO just landed and posted this here
по количеству комментариев с 5:30 до 7:30
Хмм. Понятно, что перед выходом из дома на работу. Но неужели у большинства есть силы соображать и что-то комментить в это время? То ли дело обед. В общем, неожиданно.
Важно тут также учитывать аудиторию и часовые пояса.
Скажем, вот распределение населения РФ по часовым поясам:
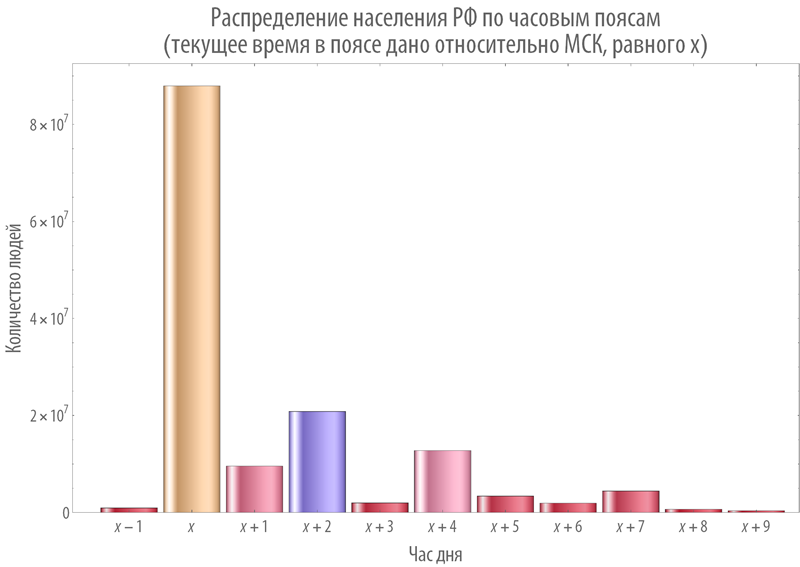
Ясно, что если в статье использовали время МСК (скорее всего), то когда в Москве 6 утра, условно, в РФ уже на Дальнем Востоке день к концу идет.
Учитывая это, не так удивительно, что ранние посты читаются активно.
Код на языке Wolfram Language для получения инфографики:
Скажем, вот распределение населения РФ по часовым поясам:

Ясно, что если в статье использовали время МСК (скорее всего), то когда в Москве 6 утра, условно, в РФ уже на Дальнем Востоке день к концу идет.
Учитывая это, не так удивительно, что ранние посты читаются активно.
Код на языке Wolfram Language для получения инфографики:
Подробнее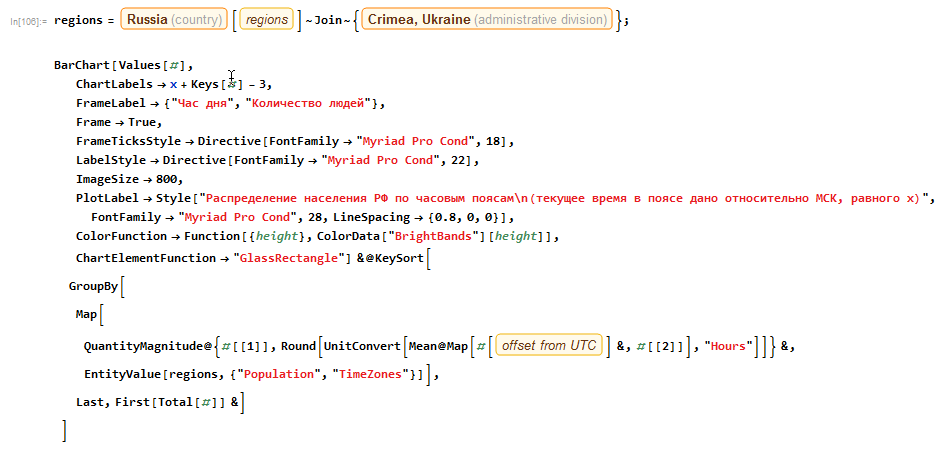
Для копирования:
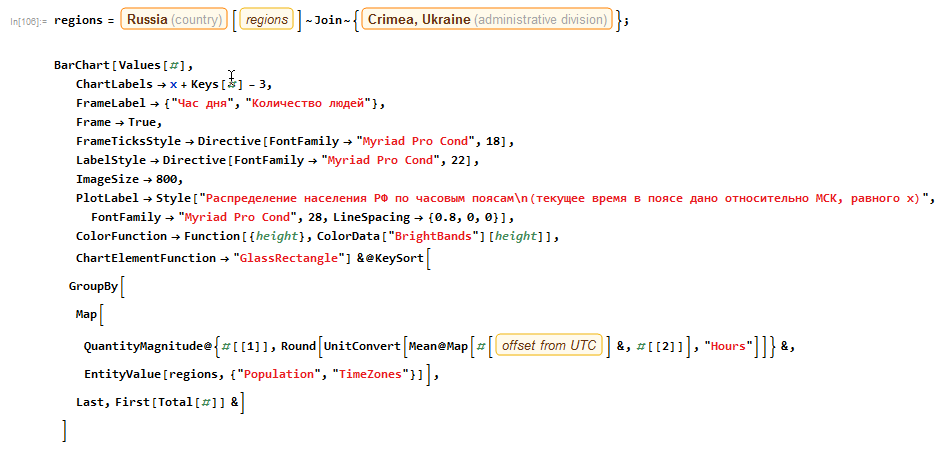
Для копирования:
regions =
Entity["Country", "Russia"][
EntityProperty["Country", "AdministrativeDivisions"]]~
Join~{Entity["AdministrativeDivision", {"Crimea", "Ukraine"}]};
BarChart[Values[#],
ChartLabels -> x + Keys[#] - 3,
FrameLabel -> {"Час дня", "Количество людей"},
Frame -> True,
FrameTicksStyle -> Directive[FontFamily -> "Myriad Pro Cond", 18],
LabelStyle -> Directive[FontFamily -> "Myriad Pro Cond", 22],
ImageSize -> 800,
PlotLabel ->
Style["Распределение населения РФ по часовым поясам\n(текущее \
время в поясе дано относительно МСК, равного x)",
FontFamily -> "Myriad Pro Cond", 28, LineSpacing -> {0.8, 0, 0}],
ColorFunction ->
Function[{height}, ColorData["BrightBands"][height]],
ChartElementFunction -> "GlassRectangle"] &@KeySort[
GroupBy[
Map[
QuantityMagnitude@{#[[1]],
Round[UnitConvert[
Mean@Map[#[
EntityProperty["TimeZone", "OffsetFromUTC"]] &, #[[2]]],
"Hours"]]} &,
EntityValue[regions, {"Population", "TimeZones"}]],
Last, First[Total[#]] &]
]
мне нравится, очень информативно, интересно читать. спасибо
коллеги, весь ваш анализ на основе нормального распределения никуда не годится. У вас по определению Пуассон (и около него), поскольку все значения положительные. Распределение явно асимметричное (что видно даже по картинке), поэтому никакие границы от нормального распределения тут не работают — используйте хоть гамму, что ли…
Верно тут смесь распределений. Критерий удаления публикаций с очень малым количеством просмотров сформулировать сложно. Есть не только «супер-статьи», но и те, которые не привлекают никакого внимания и уходят в небытиё, спустившись в ленте «все подряд». Более правильным подходом будет анализировать статьи группами, но встает вопрос правил разделения. Для статьи «средней интересности» распределение будет стремиться к нормальному. Попадание в «лучшие» меняет распределение, нужна метка «был в ТОПе»
Как Вы считаете применима центральная предельная теорема в этом случае? Мы пришли к выводу о доминирующем влиянии фактора содержания статей (фактора их интересности) и фактора попадания в ТОП. В этих условиях одного распределения может быть недостаточно. Его мы использовали для демонстрации вариабельности показателей статей, чтобы читающие думали о доверительном интервале, а не о математическом ожидании.
Ко всем данным были применены одни и те же правила, потом показатели групп данных сравнили между собой и сделали выводы. Скорее суть статьи в сравнении показателей, а не в абсолютных значениях.
Как Вы считаете применима центральная предельная теорема в этом случае? Мы пришли к выводу о доминирующем влиянии фактора содержания статей (фактора их интересности) и фактора попадания в ТОП. В этих условиях одного распределения может быть недостаточно. Его мы использовали для демонстрации вариабельности показателей статей, чтобы читающие думали о доверительном интервале, а не о математическом ожидании.
Ко всем данным были применены одни и те же правила, потом показатели групп данных сравнили между собой и сделали выводы. Скорее суть статьи в сравнении показателей, а не в абсолютных значениях.
Вот графическая интерпретация мысли
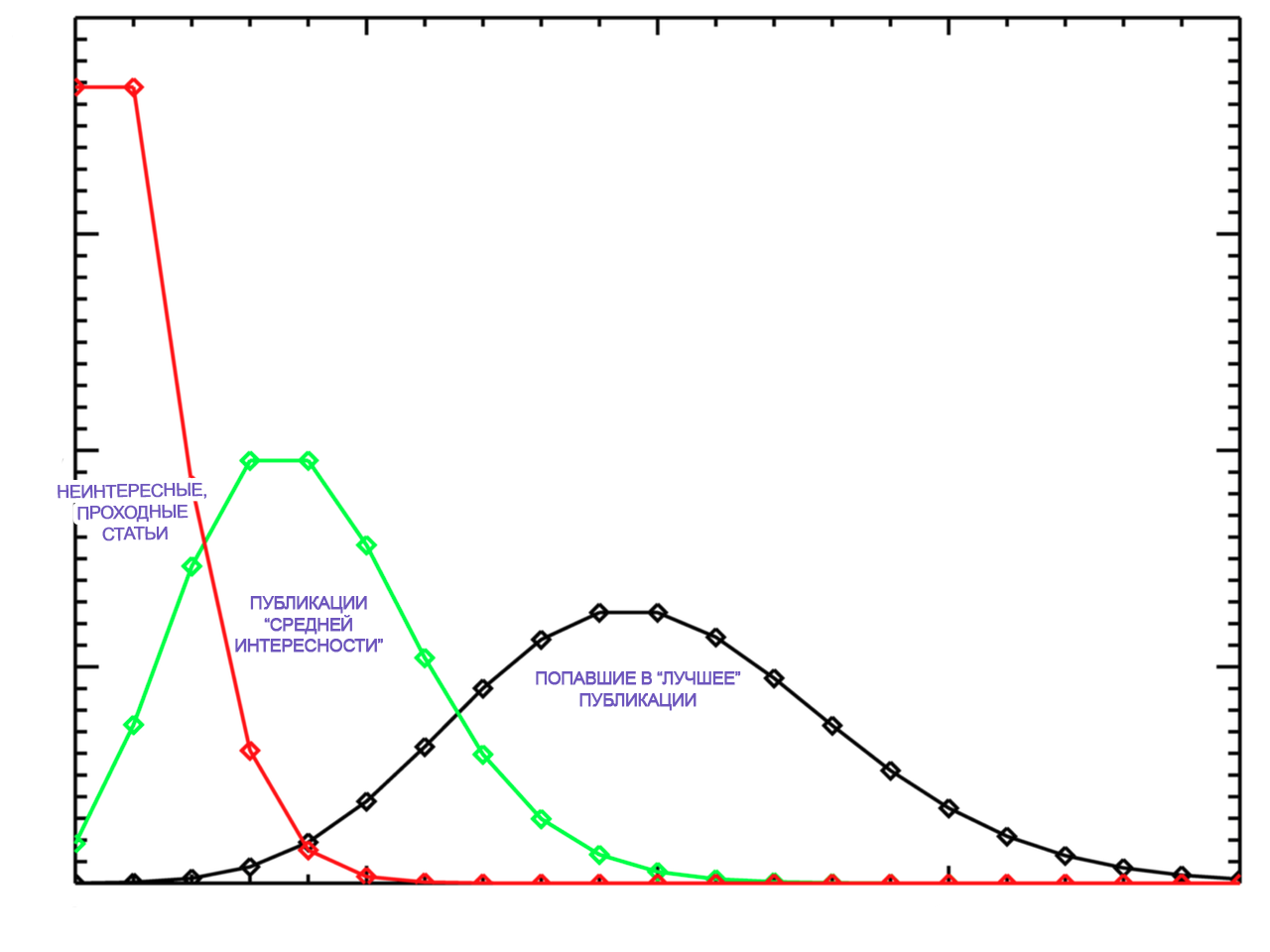
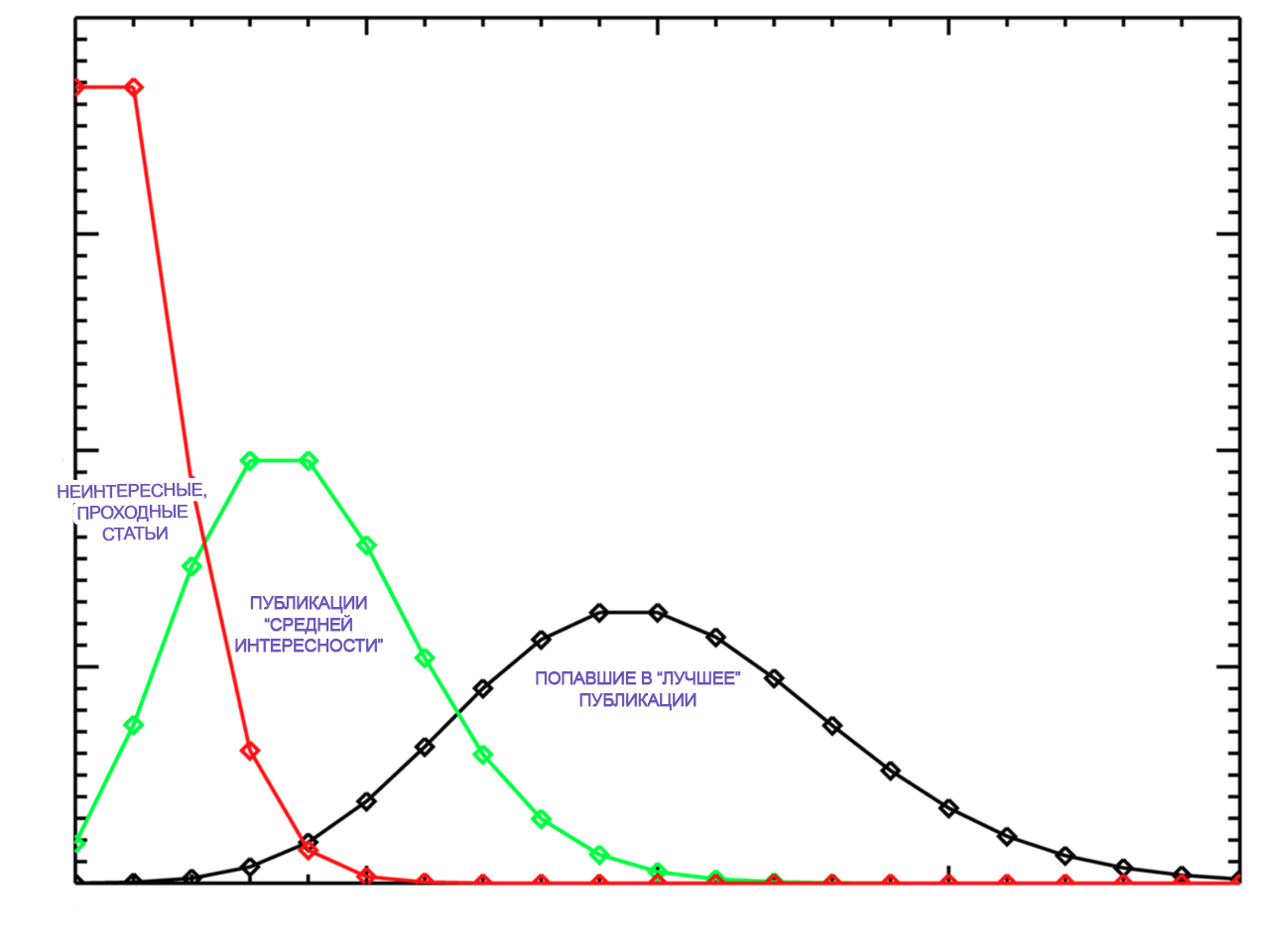
Ваша картинка лишний раз подтверждает, что имеет место Пуассон, который с ростом среднего сходится к нормальному. Чем меньше среднее, тем более несимметричное распределение имеет место (графики визуально похожи на чистое распределение Пуассона, но нужно считать модель, и проверять адекватность). Похоже, ничего выкидывать не нужно, нужно строить обычную модель GLMM, из которой и получать ответы на все вопросы — что от чего и как зависит, где разница/влияние значимо, где нет, и т.д., и т.п… Можно потом динамику привинтить, оценку взаимодействия факторов, и т.д. Данные вообще открытые?
Число наступлений определённого случайного события за единицу времени, когда факт наступления этого события в данном эксперименте не зависят от того, сколько раз и в какие моменты времени оно осуществлялось в прошлом, и не влияет на будущее. А испытания производятся в стационарных условиях, то для описания распределения такой случайной величины обычно используют закон Пуассона.
Как вы считаете, зависит число просмотров публикации от уже набранного числа просмотров, при условии что на Хабре поведение показателей статьи сильно изменяется после выхода статьи в «лучшее»?
Можно использовать распределение, предназначенное, например, для расчета количества проезжающих машин по участку дороги за единицу времени, в данном случае?
Приход одного читателя в течение любого интервала не зависит от прихода любого другого читателя в течение любого другого интервала? Зависит, а чтобы использовать распределение Пуассона, не должно зависеть.
Метод подбора распределения для явления с комплексной структурой внутри по внешнему виду распределения неверный.
В статье есть ссылка для получения таблицы Excel с данными, которые мы собрали для публикации.
Схожим является распределение высоты деревьев, оно нормальное. Это распределение получено в результате того, что деревья росли, как росли показатели статей. Статьи как три типа деревьев:
1) неинтересные статьи — деревья, которые засохли (норм. расп. более вероятно, чем расп. Пуассона)
2) средней интересности статьи — деревья, которые росли в нормальных условиях (норм. расп.)
3) попавшие в лучшее статьи — деревья, которым давали удобрения или растущие в очень благоприятных условиях (норм. расп.)
1) неинтересные статьи — деревья, которые засохли (норм. расп. более вероятно, чем расп. Пуассона)
2) средней интересности статьи — деревья, которые росли в нормальных условиях (норм. расп.)
3) попавшие в лучшее статьи — деревья, которым давали удобрения или растущие в очень благоприятных условиях (норм. расп.)
кратко: это не распределение Пуассона
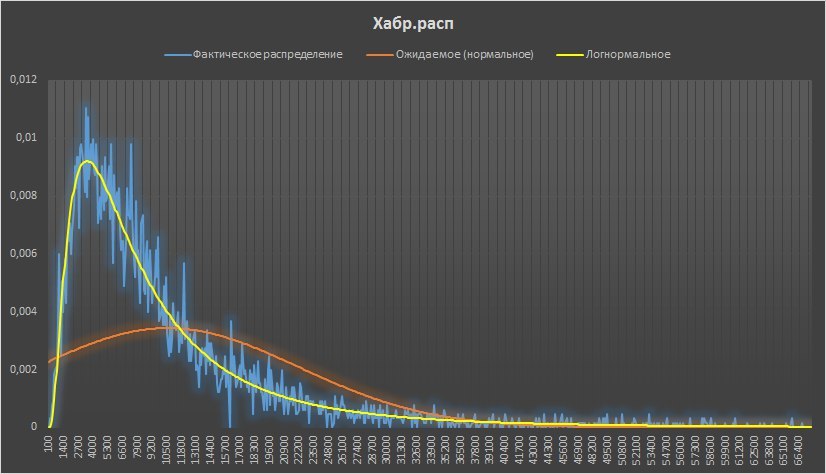
Распределение подобрать можно, оно логнормальное, для этого распределения получается, что мы работали не с 99,7% распределения, а с 92% публикаций.
Меняются ли от этого выводы — нет (только абсолютные значения доверительных интервалов, но не их соотношения (больше или меньше) между друг другом)…
" с 92% публикаций." — с 92% распределения.
У меня вопрос про «выводы не меняются»
Вы серьёзно считаете, что тут всё хорошо и правильно?
PS Спасибо на том, что видимо всё-таки кто-то с пониманием статистики посмотрел, что вы тут понаписали…
Публикации мы удаляли до тех пор, пока все они не укладывались в μ+3σ.
Вы серьёзно считаете, что тут всё хорошо и правильно?
PS Спасибо на том, что видимо всё-таки кто-то с пониманием статистики посмотрел, что вы тут понаписали…
Нужно было не просто учитывать количество просмотров, а количество просмотров на единицу времени. Так данные были бы точнее и не включали бы в себя «супер-статьи» которые за короткий промежуток времени набирают много просмотров и те статьи, которые за большое количество времени не собрали просмотров вообще.
Когда запилят АПИ для получения инфы о статьях?
«Лучшее время
по количеству просмотров с 23:30 до 00:00
по количеству добавлений в избранное с 6:30 до 8:30»
На унитазе добавляем, в кроватке перед сном читаем.
по количеству просмотров с 23:30 до 00:00
по количеству добавлений в избранное с 6:30 до 8:30»
На унитазе добавляем, в кроватке перед сном читаем.
Sign up to leave a comment.
Анализ публикаций на Хабрахабре за последние полгода. Статистика, полезные находки и рейтинги