Сортировки слиянием

Сортировки слиянием работают по такому принципу:

1. Ищутся (как вариант — формируются) упорядоченные подмассивы.
2. Упорядоченные подмассивы соединяются в общий упорядоченный подмассив.

Сам по себе какой-нибудь упорядоченный подмассив внутри массива не имеет особой ценности. Но если в массиве мы найдём два упорядоченных подмассива, то это совершенно другое дело. Дело в том, что очень быстро и с минимальными затратами можно произвести над ними слияние — сформировать из пары упорядоченных подмассивов общий упорядоченный подмассив.



Как видите, объединить два упорядоченных массива в один не просто, а очень просто. Нужно двигаться одновременно в обоих массивах слева-направо и сравнивать очередные пары элементов из обоих массивов. Меньший элемент отправляется в общий котёл. Когда в одном из массивов элементы заканчиваются, оставшиеся элементы из другого массива просто по порядку переносятся в главный список.

В этом-то и соль алгоритмов данного класса. Изначально рандомный массив можно разбить на множество небольших упорядоченных подмассивов. При попарном слиянии количество упорядоченных подмассивов уменьшается, длина каждого из них увеличивается. На последнем шаге массив представляет из себя всего два упорядоченных подмассива, которые сливаются в единую упорядоченную структуру.


Автором данной концепции является Джон фон Нейман. Иногда встречается спорное утверждение, что сортировку он придумал во время работы над Манхеттенским проектом, поскольку перед ним стояла задача обеспечить эффективные расчёты огромного количества статистических данных при разработке ядерной бомбы. Сложно оценить правдоподобность данной версии, поскольку первые его работы по сортировке слиянием датируются 1948 годом, а создание бомбы были завершено 3-мя годами раннее. Впрочем, что же там за атомная сортировка, давайте на неё взглянем.

Естественное неймановское слияние

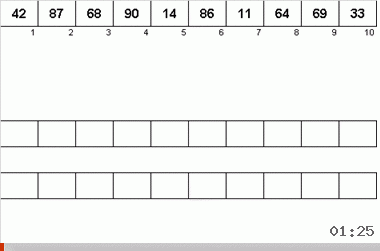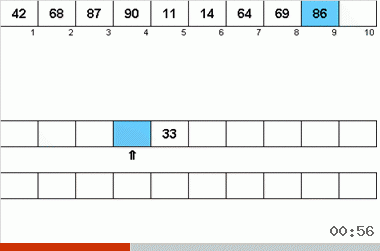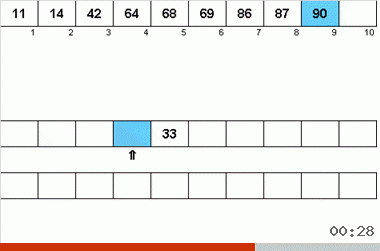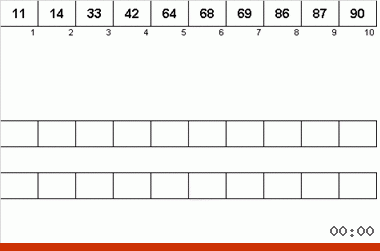
На неймановский алгоритм повлияли конструктивные особенности компьютеров 40-х годов. Выглядело это так:

1. Всего используется три магнитные ленты — основная, на которой записаны неотсортированные данные и две вспомогательные.
2. Данные последовательно считываются с основной ленты.
3. Пока последовательно считываемые данные представляют из себя упорядоченный подмассив, они переписываются на одну из вспомогательных лент.
4. Как только завершается очередной отсортированный подмассив (т.е. на основной ленте встречается элемент, меньший чем предыдущий), на вспомогательной ленте ставится указатель (конец подмассива) и происходит переключение на другую вспомогательную ленту.
5. Пункты 2-4 повторяются снова, только данные переносятся уже на другую вспомогательную ленту. При завершении очередного упорядоченного подмассива на основной ленте происходит поочерёдное переключение то на одну вспомогательную ленту, то на другую.
6. Когда все данные с основной ленты считаны, происходит обработка вспомогательных лент.
7. С обеих вспомогательных лент поочерёдно считываются данные.
8. При этом очередные данные с двух лент сравниваются между собой. По результатами сравнения на основную ленту записывается меньший элемент из пары.
9. Так как границы массивов на вспомогательных лентах отмечены указателями, считывание и сравнение происходит только в пределах отсортированных подмассивов.
10. Если на одной из вспомогательных лент закончились элементы очередного подмассива, то с оставшейся ленты остаток подмассива просто переносится на основную ленту.
11. Повторяем весь процесс заново до тех пор, пока данные на основной ленте не будут собой представлять полностью упорядоченный массив.

Неймановская сортировка является адаптивным алгоритмом: она не просто фиксирует отсортированные куски массива, но и в первую очередь старается увеличить их, чтобы затем на основе удлинённых упорядоченных подмассивов формировать ещё более длинные упорядоченные подмассивы. Поэтому её ещё называют адаптивной сортировкой слиянием.

Сложность данного алгоритма скромна — O(n²), и, тем не менее, для пионеров ламповых вычислений это был прорыв.

На примере этой первой сортировки слиянием уже виден недостаток этого класса алгоритмов — расходы на дополнительную память. В этом плане почти все сортировки слиянием дополнительно требуют O(n), однако изредка встречаются элегантные исключения.

Прямое слияние Боуза-Нельсона

Строго говоря, алгоритм Боуза-Нельсона — это сортировочная сеть, а не сортировка. В процессе массив и все его подмассивы делятся пополам и ничто не препятствует тому, чтобы все эти половинки на всех этапах обрабатывались параллельно. Однако можно представить и в виде именно сортировки. А до темы сортировочных сетей мы когда-нибудь доберёмся тоже.

1. Массив делится пополам — на левую и правую половины.
2. Элементы разбиваются на группы.
3. На первой итерации это двойки элементов (1-й элемент левой половины + 1-й элемент правой половины, 2-й элемент левой половины + 2-й элемент правой половины и т.д.), на второй итерации — четвёрки элементов (1-й и 2-й элементы левой половины + 1-й и 2-й элементы правой половины, 3-й и 4-й элементы левой половины + 3-й и 4-й элементы правой половины и т.д.), на третьей — восьмёрки и т.д.
4. Элементы каждой группы из левой половины являются отсортированным подмассивом, элементы каждой группы из правой половины также являются отсортированным подмассивом.
5. Производим слияние отсортированных подмассивов из предыдущего пункта.
6. Возвращаемся в пункт 1. Цикл продолжается до тех пор, пока размеры групп меньше размера массива.

Может показаться, что и тут требуется дополнительная память. Но нет! Для более понятного восприятия в анимации левая и правая половины массива расположены друг на другом, чтобы очевиднее было взаимное расположение сравниваемых подмассивов. Однако ввиду строгого деления пополам возможен алгоритм, при котором все сравнения и обмены делаются на месте, без привлечения дополнительных ресурсов по памяти. Что весьма нестандартно для сортировки слиянием.

def bose_nelson(data):
    m = 1
    while m < len(data):
        j = 0
        while j + m < len(data):
            bose_nelson_merge(j, m, m)
            j = j + m + m
        m = m + m
    return data

def bose_nelson_merge(j, r, m):
    if j + r < len(data):
        if m == 1:
            if data[j] > data[j + r]:
                data[j], data[j + r] = data[j + r], data[j]
        else:
            m = m // 2
            bose_nelson_merge(j, r, m)
            if j + r + m < len(data):
                bose_nelson_merge(j + m, r, m)
            bose_nelson_merge(j + m, r - m, m)
    return data

Таки есть во всех сортировках слиянием нечто, что роднит их с водородной бомбой. Сначала происходит деление, потом синтез.

Ссылки

Merge / Слияние

Статьи серии:

• Excel-приложение AlgoLab.xlsm
• Сортировки обменами
• Сортировки вставками
• Сортировки выбором
• Сортировки слиянием
  • Сбалансированное слияние сверху-вниз и снизу-вверх
  • Многофазная сортировка слиянием
  • Каскадная сортировка слиянием
  • Осциллирующая сортировка слиянием
  • Нитевидная и несмешиваемая сортировки
  • Сравнение сортировок слиянием
• Сортировки распределением
• Гибридные сортировки

Обе упомянутые в сегодняшней статье сортировки теперь доступны в приложении AlgoLab (кто изучает алгоритмы с помощью этого Excel-приложения — обновите файл). А всего через пару дней, с выходом скорого продолжения о сортировках слияния, будут доступны ещё несколько алгоритмов этого класса.

Для сортировки Боуза-Нельсона поставлено ограничение — размер массива должен быть степенью двойки. Если это условие не будет выполнено, то макрос обрежет массив до подходящего размера.

Статья написана при поддержке компании EDISON Software, которая пишет софт 3d-реконструкции и занимается разработкой сложного измерительного оборудования.