Продолжаем знакомиться с таким методом ускорения проектирования как суррогатное моделирование. Это перевод отличной статьи авторства Шуая Гуо, который мы дополнили своим кодом на MATLAB, а также некоторыми размышлениями. Если у вас получится повторить пример, или есть интересная задача, которую можно было бы решить таким образом – зовем высказаться в комментариях, нам будет что обсудить!

В первой части этой серии статей мы обсудили идею использования суррогатных моделей для ускорения такого этапа проектирования изделий как имитационное моделирование. Основной метод здесь – обучение статистической модели, которая будет служить дешевым, но точным заменителем имитационных моделей при выполнении различных задач проектирования, что значительно повышает эффективность анализа.
В части II мы рассмотрим конкретный пример, чтобы продемонстрировать, как использовать суррогатные модели на практике. Дорожная карта для этого примера показана ниже:
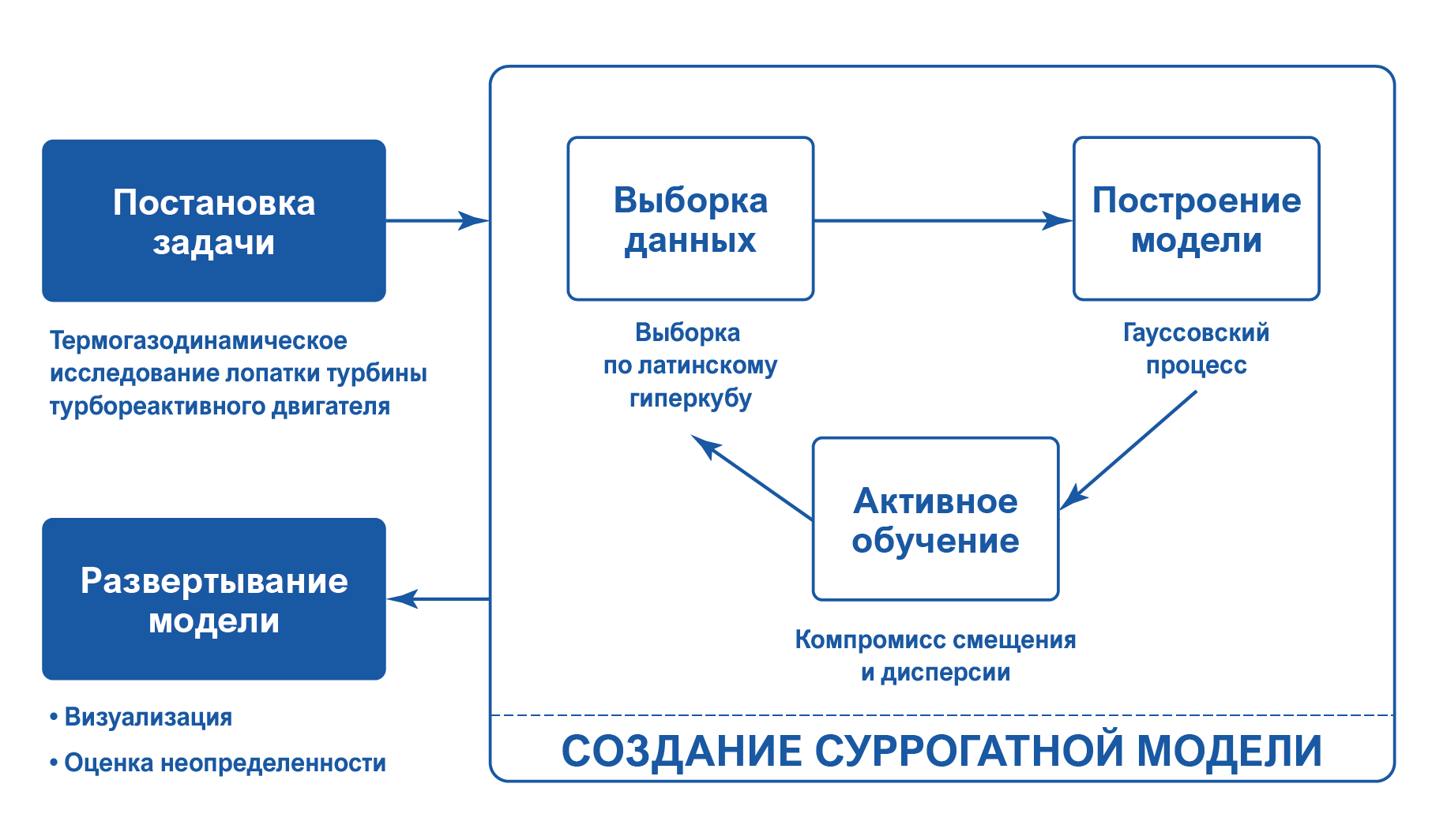
Мы начнем с изложения изучаемой проблемы, а затем применим к ней метод суррогатного моделирования. В конце мы проиллюстрируем, как использовать обученную суррогатную модель для выполнения двух типов анализа.
1. Постановка задачи
Турбина – один из ключевых компонентов турбореактивного двигателя. Горячие газы из камеры сгорания попадают на лопатки турбины, их энергия поддерживает обороты ротора, что в конечном итоге позволяет двигателю генерировать энергию и создавать тягу.
Лопатки турбины работают в чрезвычайно жестких условиях, поскольку они непосредственно сталкиваются с высокотемпературными выхлопными продуктами горения. Экстремальные температуры могут расплавить материал лопаток и поставить под угрозу надежную работу реактивного двигателя.
Как следствие, тепловой анализ является необходимостью для проектирования лопаток турбины. Для этого обычно строится физическая модель для имитации распространения энергии и оценки температурного поля внутри лопатки, учитывая в качестве граничных условий температуры сгоревшего газа и охлаждающего воздуха внутри лопатки.
В данном примере мы используем следующую схему анализа: в качестве входных переменных мы рассматриваем температуру сгоревшего газа и охлаждающего воздуха и соответствующие коэффициенты теплопроводности на границе сред. Нас интересует прогнозирование максимальной температуры лопатки (выход) с учетом входных значений.
На среднем персональном компьютере один прогон такой модели занимает 1-2 секунды.
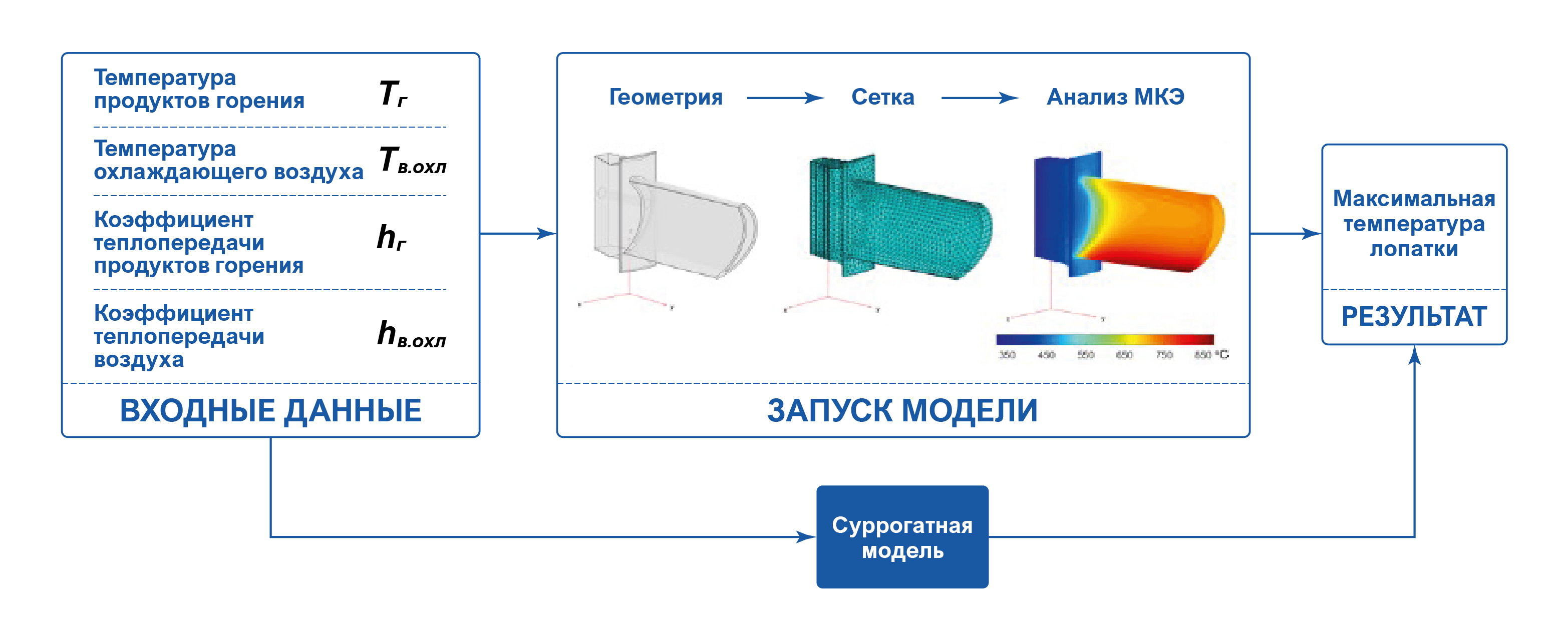
2. Суррогатное моделирование
Для проектирования лопаток может потребоваться много прогонов модели, чтобы понять, как лопатка реагирует на различные значения температуры газа, температуры охлаждающего воздуха и соответствующие коэффициенты теплопроводности. Одним из способов ускорить этот процесс является обучение суррогатной модели перед началом «медленного» моделирования. Именно это мы и собираемся сделать в данном примере.
Исходные данные для этого примера доступен на сайте MathWorks и входит в стандартную поставку MATLAB.
Чтобы запустить пример, бросьте файл Blade.stl в папку с проектом, создайте LiveScript, и можно начинать!
На основе этого примера мы создадим свою "дорогостоящую и сложную" (хотя и учебную) модель для расчета максимальной температуры лопатки при следующих входных условиях:
изменяемая температура набегающего потока газа и температура потока охлаждающего воздуха, поступающего изнутри лопатки;
изменяемая теплопроводность на границе сред воздух-металл по "горячей стороне" и по "холодной стороне" лопатки.
function max_temp = getMaxTemp(args)
h_air = args(1); T_air = args(2); h_gas = args(3); T_gas = args(4);
% Создаем модель температурного состояния
thermalmodel = createpde('thermal','steadystate');
% Импортируем геометрию лопатки и создаем сетку
importGeometry(thermalmodel,'Blade.stl');
msh = generateMesh(thermalmodel,'Hmax',0.01);
thermalmodel.Mesh = msh;
% Материал лопатки (в примере это сплав никеля NIMONIC 90)
kapp = 11.5; % зададим теплопроводность в Вт/м/К
thermalProperties(thermalmodel,'ThermalConductivity',kapp);
% Задать граничные условия – температуру и теплопроводность на гранях
thermalBC(thermalmodel,'Face',[15 12 14], 'ConvectionCoefficient',h_air, 'AmbientTemperature',T_air ); % Поток охлаждающего воздуха
thermalBC(thermalmodel,'Face',[11 10 13 1], 'ConvectionCoefficient',h_gas, 'AmbientTemperature',T_gas ); % Поток горячих газов
thermalBC(thermalmodel,'Face',[6 9 8 2 7], 'ConvectionCoefficient',15, 'AmbientTemperature',400 ); % Воздух у основания лопатки
% База лопатки, через которую тепло уходит к другим частям ротора
thermalBC(thermalmodel,'Face',[3 4 5], 'ConvectionCoefficient',1000, 'AmbientTemperature',300);
% Запустить модель
Rt = solve(thermalmodel);
% Осталось только взять максимум
max_temp = max(Rt.Temperature);
endВсе параметры заданы для соответствующих граней модели лопатки (для дальнейших уточнений предлагаем ознакомиться с исходным примером).
2.1 Исходные данные
Для начала мы генерируем несколько обучающих примеров для обучения суррогатной модели.
% Важно закрепить seed для воспроизводимости результатов
rng default;
% Сколько точек используем для исходного набора данных
n_initial_lhs_points = 8;
% Подписи входных переменных для графиков
var_labels = { 'h_{в.охл}', 'T_{в.охл}', 'h_{г}', 'T_{г}' };
% Границы наших входных параметров
var_limits = [[20, 40]; [120, 180]; [30, 70]; [800, 1200]];
% Распределение по латинскому квадрату
LS = lhsdesign( n_initial_lhs_points, 4 );
X = rescale( LS, ...
repmat( var_limits(:,1)', [ls_max_points,1] ), ...
repmat( var_limits(:,2)', [ls_max_points,1] ));На этом этапе полезно, чтобы точки в распределении были равномерно распределены по всему пространству входных параметров. Для этого будем использовать схему выборки латинского гиперкуба.
В рамках примера сгенерируем всего 8 точек для начальной выборки.
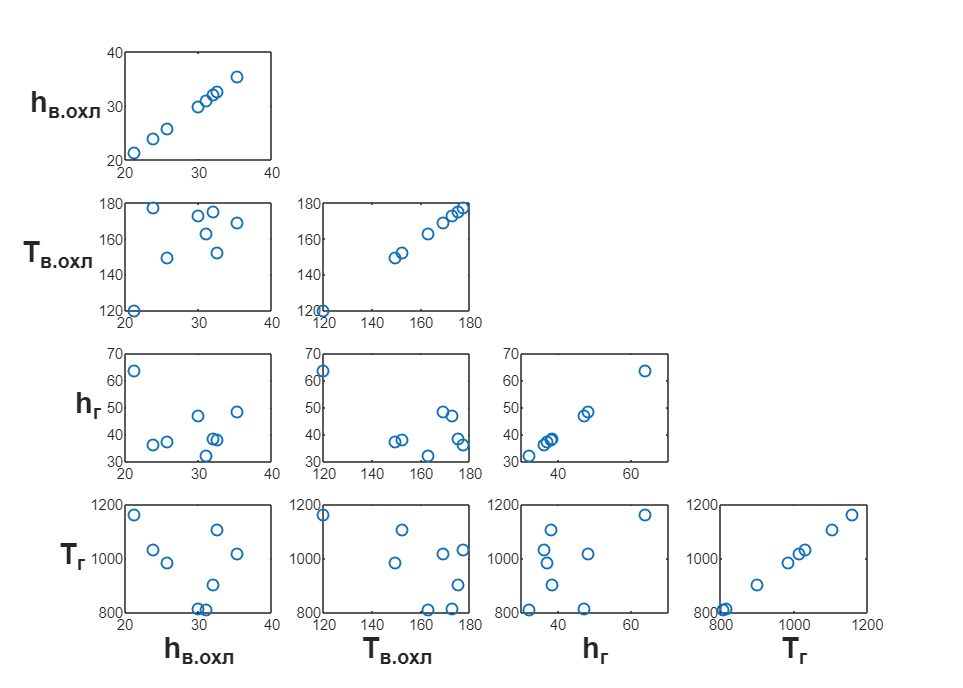
Теперь мы можем перейти к следующему шагу.
2.2 Обучение модели
На основе первоначально сгенерированных образцов мы можем обучить суррогатную модель. В данном случае в качестве суррогатной модели мы выбрали гауссовский процесс (GP). Используем функцию getMaxTemp для генерации вектора таргетов y.
y = zeros([size(X, 1), 1]);
for i = 1:size(X, 1)
y(i) = getMaxTemp(X(i,:));
endОсновная мотивация в выборе GP-модели заключается в том, что, в отличие от многих других методов машинного обучения с учителем, GP выдает предсказания на неразмеченных образцах, оценивая при этом статистическую неопределенность предсказания в новых точках. Эта особенность является ключом к активному обучению, к которому мы как раз переходим.
2.3 Активное обучение
Итак, мы хотим улучшить первоначальную суррогатную модель с помощью дополнительных обучающих примеров. Мы делаем это итеративно, на каждой итерации генерируем только одну пару «X ; y» (наши признаки – это 4 упомянутых выше проектных параметра, наша целевая переменная: максимальная температура) и добавляем ее к существующему набору обучающих данных.
Чтобы определить, какие точки нужно добавить к датасету, мы ищем в пространстве входных параметров такие области, где текущая суррогатная модель имеет наибольшую оценку ошибки предсказания (confidence interval, CI).
Нам нужны именно те точки, в которых текущая суррогатная модель «чувствует себя наименее уверено» относительно своего прогноза.
Есть много способов поиска таких точек, их выбор определяется поведением модели, характером датасета и т.д. Для упрощения изложения покажем наиболее часто встречающийся алгоритм: поиск наилучше точки по сетке (для комбинаторики используем пакет Combinator):
function [max_args, max_yci, max_ypred] = ...
findMaxCIPoint_grid(mdl, limits, grid_steps)
% Все пермутации для 4-х векторов параметров модели (индекс)
idx_grid = combinator(grid_steps, size(limits,1), 'p','r');
% Масштабируем сетку от интервала 0..1 до размера пространства входных параметров
N = size(idx_grid,1);
X_grid = rescale( idx_grid, ...
repmat(limits(:,1)', [N,1]), ...
repmat(limits(:,2)', [N,1]) );
% Получаем предсказание для всех комбинаций по сетке
[ypred_grid, yci_grid] = predict(mdl, X_grid);
% Находим точку с максимальной неопределенностью
[max_yci,idx] = max(yci_grid);
max_args = X_grid(idx, :);
max_ypred = ypred_grid(idx, :);
endДисклеймер: мы исследовали разные методы активного обучения, пока победила рандомизация и градиентный спуск.
К слову об оптимизации, суррогатные модели можно использовать ещё одним интересным образом – для суррогатной оптимизации, хотя на моделирование этот метод вроде бы не переносится. Если автор автор метода ответит на наши письма, мы сообщим! :)
Выбирая новые точки из пространстве параметров именно в тех областях, где предсказание модели делает наибольшую ошибку, суррогатная модель сможет «обучаться» быстрее всего.
% Для воспроизводимости кода:
n_grid_steps = 31; % шаг разбиения пространства для grid search
n_max_added_points = 20; % Сколько точек мы добавим к датасету
% Установим параметры GP-модели
opts = { 'BasisFunction','constant', ...
'KernelFunction','rationalquadratic'};
% Датасет для накопления точек будет храниться в переменных X_new и y_new
X_new = zeros(size(X,1)+n_max_added_points, size(X,2));
y_new = zeros(size(y,1)+n_max_added_points, 1);
X_new(1:size(X,1), 1:size(X,2)) = X;
y_new(1:size(y,1),:) = y;
% Обучаем модель на исходных данных
gprMdl = fitrgp(X, y, opts{:});
% Сохраним предсказания и оценку ошибок модели перед добавлением новых данных
[initial_ypred, initial_confidence_intervals] = resubPredict(gprMdl);
for i = 1:n_max_added_points
% Поиск точки с наибольшей потенциалной информацией
[best_args, max_yci, max_ypred] = ...
findMaxCIPoint_grid(gprMdl, var_limits, n_grid_steps);
% Запускаем "тяжелую" модель и дополняем датасет новыми параметрами
X_new(size(X,1)+i, :) = best_args;
y_new(size(y,1)+i, :) = getMaxTemp(best_args, tmodel);
% Заново обучаем модель на дополненном датасете
gprMdl = fitrgp(X_new(1:size(X,1)+i,:), y_new(1:size(y,1)+i,:), opts{:} );
% Сохраняем прогнозы и ошибки новой обученной модели
[ypred, yci] = resubPredict(gprMdl);
endИногда, после добавления лишь десятка дополнительных обучающих примеров, мы добивались того, чтобы окончательная ошибка предсказания падала ниже 3% от начального значения. Обычно, наши цели требовали добавления лишь 10-20 новых точек в датасет.
Одним из факторов успеха было исходное распределение точек, которое зависит от настройки генератора случайных чисел (seed). Это известная проблема, хорошо знакомая все в data science. :)
Для дискуссии, вот примеры графиков поиска точек с наибольшей информативностью в пространстве:
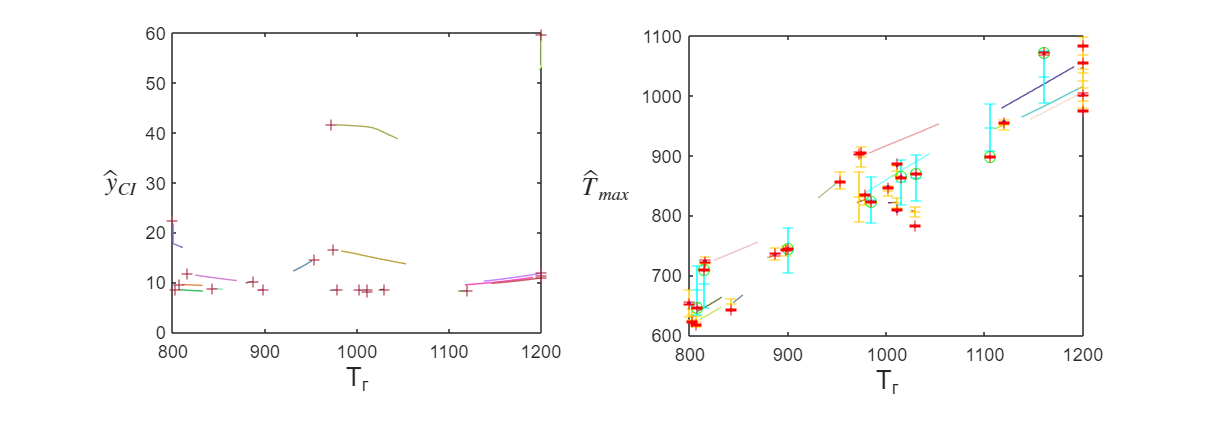
2.4 Испытания
Чтобы оценить точность модели, создаем тестовый набор данных, содержащий 20 тестовых образцов. Построим график чтобы сопоставить прогнозы разных моделей, тяжелой и легкой:
figure
[ypred,yci] = resubPredict(gprMdl);
plot(y_new, ypred, 'bo');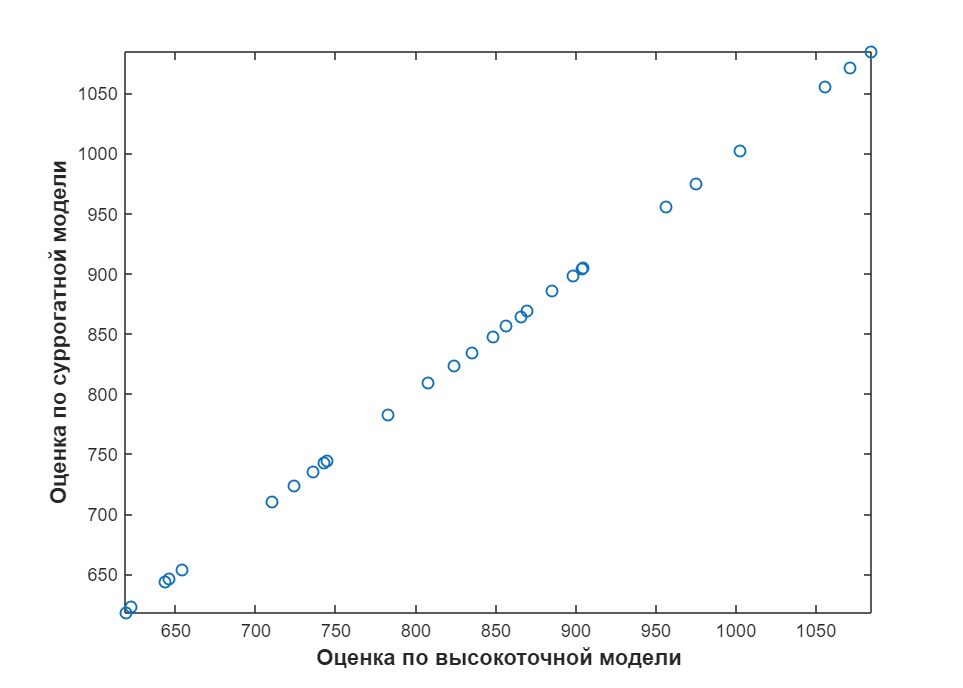
Видно, что данные, полученные из суррогатной модели, прекрасно сопоставляются с данными по исходной высокоточной модели, поскольку все предсказания полностью совпадают с результатами моделирования (грубых ошибок нет, а точность соответствия можно повышать до нужных значений при помощи активного обучения).
3. Развертывание модели
Теперь, когда мы обучили нашу суррогатную модель и оценили ее точность предсказания, пришло время развернуть ее для выполнения нужных нам задач анализа.
3.1 Визуализация
Суррогатная модель может легко быть использована для визуализации «ландшафта» функции «вход-выход». Это помогает аналитикам быстро выявить важные зависимости между выходом и различными входами.
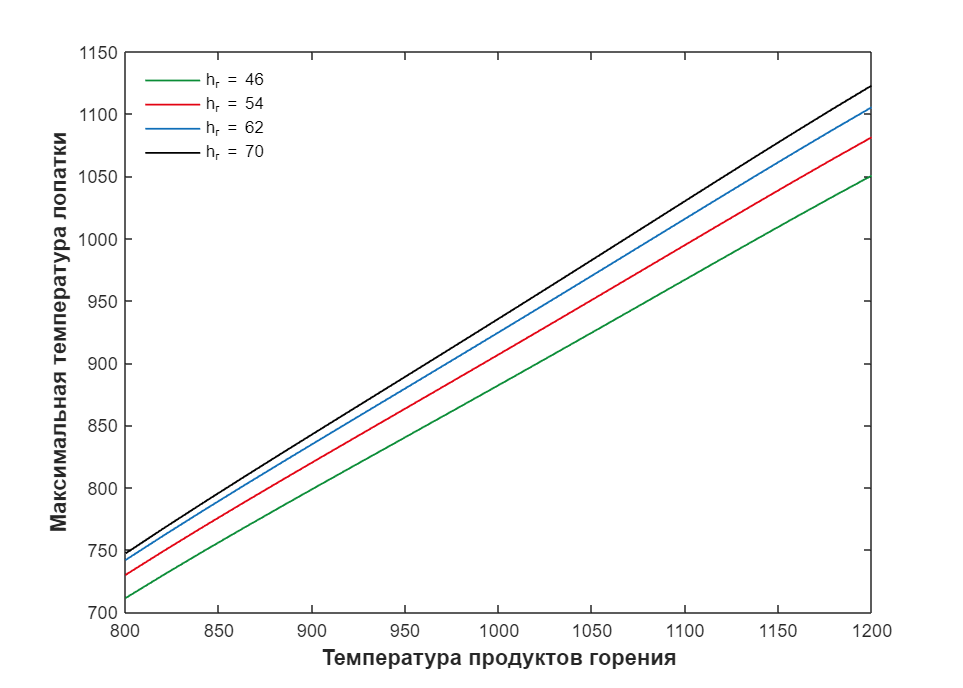
Например, на этом графике показана зависимость между температурой газа и максимальной температурой лопатки при различных значениях коэффициента теплопроводности.
Видно, что температура лопатки почти линейно зависит от температуры газа: при повышении температуры газа температура лопатки пропорционально увеличивается, что имеет интуитивный смысл.
Также мы видим, что связь между температурой лопатки и коэффициентом теплопроводности газа немного нелинейна в режиме высоких температур. Шаг увеличения максимальной температуры лопатки начинает снижаться относительно шага увеличения температуры продуктов горения, если при этом сохраняется коэффициент теплопроводности. То же самое происходит с каждым следующим шагом повышения коэффициента теплопроводности.
3.2 Количественная оценка неопределенности
На практике условия эксплуатации турбины постоянно меняются. То есть мы не уверены в точных значениях температур газа и охлаждающего воздуха и связанных с ними коэффициентов теплопроводности. В результате нам необходимо оценивать характер изменения характеристик нашего продукта, вызванное неопределенными условиями эксплуатации. Именно этого и помогает добиться анализ количественной оценки неопределенности.
Обычно для количественного анализа неопределенности мы используем метод Монте-Карло.
В двух словах, метод Монте-Карло начинается с назначения распределений вероятностей неопределенным входным переменным (распределения выражают наши текущие знания о том, насколько эти переменные «не определены»). Затем мы берем большое количество случайных точек (~o(10⁴)) из входного распределения и вычисляем соответствующие им выходные значения. На основе ансамбля выходных результатов мы можем построить гистограмму выхода, которая статистически полно описывает неопределенность выходных переменных.
Для проведения Монте-Карло анализа последуем вышеупомянутым процедурам. Предположим, что наши четыре входа независимы и имеют нормальное распределение (что на графике). Мы берем в общей сложности 10000 случайных точек, чтобы выполнить количественную оценку неопределенности.


Распределение максимальной температуры лопатки, предсказанное суррогатной моделью, показано на графике. Также мы сравниваем этот результат с распределением, полученным путем применения процедуры Монте-Карло непосредственно к исходной высокоточной модели. Видим, что суррогатная модель точно оценила изменение максимальной температуры лопатки, связанное с неопределенностью входных параметров.
По временным затратам, Монте-Карло с суррогатной моделью занимает 0.0118 с на довольно стандартном i7@2.60, в то время как симуляция детальной модели заняла 2.5 часа (ускорение в 70 тыс.раз).
Средняя ошибка прогноза в этом эксперименте составила 1.15%.
Вот такого ускорения можно добиться с помощью хорошо обученной суррогатной модели.
4. Выводы
В этой статье мы рассмотрели, как использовать метод суррогатного моделирования для ускорения теплового анализа лопатки турбины реактивного двигателя. Мы продемонстрировали ключевые этапы процесса суррогатного моделирования:
Начальная выборка: метод латинского гиперкуба для создания датасета, хорошо «заполняющего пространство»
Обучение модели: Гауссовский процесс
Активное обучение: последовательное обогащение обучающей выборки для максимизации эффективности обучения модели
Тестирование модели: сравнительный анализ с использованием тестового набора данных
Развертывание модели: визуализация зависимостей и анализ количественной оценки неопределенности